Задание на проектирование
 Скачать 372.57 Kb. Скачать 372.57 Kb.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Тип НО | Переходное ослабление, дБ | Рабочая частота, f0, ГГц | Тип линии | Подложка | Проводники | |||
| толщина, мм | отн. диэл. прон. () | тангенс угла потерь tg() | толщина, мм | металл | ||||
| Шлейфный НО | 3,0 | 5,0 | МПЛ | 0,5 | 3,8 | 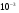 | 0,05 | Серебро |
Цель работы: Цель работы заключается в более глубокой проработке темы «Полосковые направленные ответвители», изучаемой в курсе «Техническая электродинамика». Знакомство с наиболее широко применяемыми типами направленных ответвителей, их свойствами и методами расчета, с существующими стандартами на платы для полосковых линий передачи, обучение самостоятельно выбирать тип направленного ответвителя по заданным характеристикам и производить детальный расчет полоскового направленного ответвителя с соответствующей конструкторской проработкой.
Оглавление
Задание на проектирование. 1
Аналитический электрический расчет кольцевого направленного ответвителя. 3
Определение волновых сопротивлений. 3
Конструктивный расчет кольцевого направленного ответвителя. 14
Аналитический расчет ширин отрезков, эффективной диэлектрической проницаемости и длин отрезков 14
Численный расчет в пакете MWO (утилита TXLine) 15
Построение виртуальной модели кольцевого направленного ответвителя с помощью MWO. 17
Построение схемной модели направленного ответвителя и расчет комплексных коэффициентов передачи. 17
Выводы. 27
Аналитический электрический расчет кольцевого направленного ответвителя.
Определение волновых сопротивлений.
Тогда
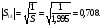
Определение волновых сопротивлений:
где
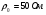 - волновое сопротивление подводящих линий.
- волновое сопротивление подводящих линий.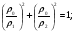
Из условия kl=π(2n+1)/2, n = 0, 1, 2, 3, … следует, что длина l должна быть равна l = λ0 /4, где λ0 – длина волны в линиях, соответствующая центральной частоте заданного рабочего диапазона.
Расчет частотных зависимостей модулей и фаз коэффициентов матрицы рассеяния для идеализированной модели НО.
ρ0
ρ0
ρ0
1
2
4
3
ρ0
l
l
l
3l
ρ1
ρ1
ρ2
ρ2
Рис. 1.3.1
ρ0
ρ0
ρ0
1
2
4
3
ρ0
l
l
l
3l
ρ1
ρ1
ρ2
ρ2
Рис. 1.3.1
ρ0
ρ0
ρ0
1
2
4
3
ρ0
l
l
l
3l
ρ1
ρ1
ρ2
ρ2
Рис. 1.3.1
1
2
3
4
ρ0
ρ0
ρ0
ρ0
ρ1
ρ2
ρ1
ρ2
l
l
Рис. 1.2.1
Шлейфный НО представляет собой два отрезка линий передачи (рис. 1.2.1) одинаковой длины l с одинаковыми волновыми сопротивлениями ρ1 между концами которых включены параллельно два шлейфа такой же длины l, но с другими волновыми сопротивлениями ρ2. К местам стыка этих линий подводятся линиипередачи с волновыми сопротивлениями ρ0 для связи с другими устройствами.
Шлейфный НО имеет две плоскости симметрии. Поэтому в матрице [S] определению подлежат только 4 комплексных коэффициента: S11, S12, S13, S14. Сама матрица [S] имеет вид:
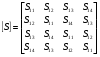 (1.2.1)
(1.2.1)При вычислений коэффициентов [S] для всех типов ответвителей будем предполагать, что плоскости, от которых отсчитываются фазы рассеяных волн, располагаются в месте стыка НО с внешними линиями.
Рассматривая синфазно-противофазные режимы питания со стороны всех каналов связи, можно получить следующие формулы для расчета всех матричных коэффициентов:
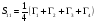 ; (1.2.2)
; (1.2.2)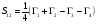 ; (1.2.3)
; (1.2.3)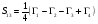 ; (1.2.4)
; (1.2.4)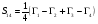 ; (1.2.5)
; (1.2.5)где
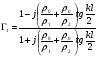 ; (1.2.6)
; (1.2.6)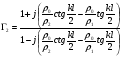 ; (1.2.7)
; (1.2.7)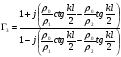 ; (1.2.8)
; (1.2.8)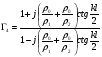 ; (1.2.9)
; (1.2.9)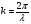 – постоянная распространения в линиях.
– постоянная распространения в линиях.Из соотношений (1.2.2) – (1.2.9) следует, что все коэффициенты матрицы (1.2.1) как функции параметра kl носят периодический характер с периодом, равным 2π . Оказывается, что условие S11=S14=0 удовлетворяется только тогда, когда одновременно выполняются следующие условия:
ctgkl= 0 ; (1.2.10)
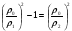 ; (1.2.11)
; (1.2.11)При выполнении условий (1.2.10) и (1.2.11)
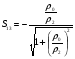 ; (1.2.12)
; (1.2.12)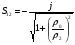 . (1.2.13)
. (1.2.13)Из условия (1.2.10) следует, что идеальная направленность (S14=0) и идеальное согласование (S11=0) могут быть достигнуты только на тех частотах, на которых длина линий кратна нечетному числу четвертей длин волн. Наибольшая широкополосность НО достигается, когда длина l равна четверти длины волны.
Несмотря на то, что на всех других частотах S11≠0 и S14≠0 модули этих величин в определенном диапазоне частот могут иметь приемлемую для практики малую величину. На рис. 1.2.2 в качестве примера приведены графики зависимостей |S11|, |S12|, |S13| и |S14| от параметра kl 3 дБ шлейфного НО.
Рис. 1.2.2
kl/
Sij
S14
S11
S13
S12
 Электрический расчет шлейфного НО сводится к определению электрической длины l, всех отрезков линий и их волновых сопротивлений ρ1 и ρ2.
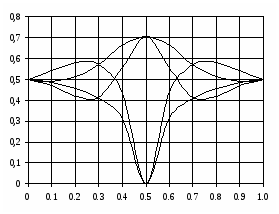
Электрический расчет шлейфного НО сводится к определению электрической длины l, всех отрезков линий и их волновых сопротивлений ρ1 и ρ2.Построение графиков модулей коэффициентов матрицы рассеяния по приведенным формулам:
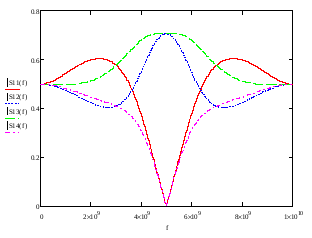
Рис.2. График зависимостей модулей коэффициентов матрицы рассеяния от частоты.
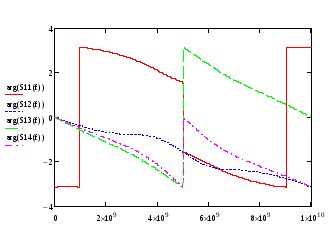
Рис.3. График зависимостей фаз коэффициентов матрицы рассеяния от частоты.
Таблица 2.
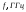 | 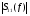 | 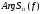 | 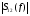 | 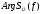 | 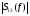 | 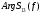 |
| 0,5 | 0.512 | -3.125 | 0.493 | -0.197 | 0.499 | -0.29 |
| 1,0 | 0.542 | 3.139 | 0.474 | -0.38 | 0.498 | -0.573 |
| 1,5 | 0.576 | 3.072 | 0.449 | -0.537 | 0.501 | -0.847 |
| 2,0 | 0.599 | 2.963 | 0.423 | -0.659 | 0.512 | -1.115 |
| 2,5 | 0.603 | 2.816 | 0.406 | -0.738 | 0.536 | -1.385 |
| 3,0 | 0.578 | 2.626 | 0.409 | -0.775 | 0.575 | -1.671 |
| 3,5 | 0.508 | 2.387 | 0.453 | -0.811 | 0.628 | -1.992 |
| 4,0 | 0.376 | 2.102 | 0.548 | -0.936 | 0.679 | -2.36 |
| 4,5 | 0.193 | 1.811 | 0.658 | -1.206 | 0.705 | -2.756 |
| 5,0 | 0 | 1.446 | 0.706 | -1.571 | 0.708 | -3.142 |
| 5,5 | 0.193 | -1.811 | 0.658 | -1.935 | 0.705 | 2.756 |
| 6,0 | 0.376 | -2.102 | 0.548 | -2.206 | 0.679 | 2.36 |
| 6,5 | 0.508 | -2.387 | 0.453 | -2.331 | 0.628 | 1.992 |
| 7,0 | 0.578 | -2.626 | 0.409 | -2.366 | 0.575 | 1.671 |
| 7,5 | 0.603 | -2.816 | 0.406 | -2.404 | 0.536 | 1.385 |
| 8 | 0.599 | -2.963 | 0.423 | -2.482 | 0.512 | 1.115 |
| 8,5 | 0.576 | -3.072 | 0.449 | -2.604 | 0.501 | 0.847 |
| 9 | 0.542 | -3.139 | 0.474 | -2.761 | 0.498 | 0.573 |
| 9,5 | 0.512 | 3.125 | 0.493 | -2.944 | 0.499 | 0.29 |
| 10 | 0.5 | 3.142 | 0.5 | -3.142 | 0.5 | 0 |
Таблица 3.
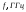 | 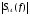 | 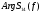 |
| 0,5 | 0.495 | -0.244 |
| 1,0 | 0.482 | -0.481 |
| 1,5 | 0.465 | -0.71 |
| 2,0 | 0.446 | 0.933 |
| 2,5 | 0.429 | -1.162 |
| 3,0 | 0.41 | -1.417 |
| 3,5 | 0.378 | -1.728 |
| 4,0 | 0.31 | -2.125 |
| 4,5 | 0.18 | -2.611 |
| 5,0 | 0 | 1.446 |
| 5,5 | 0.18 | -0.531 |
| 6,0 | 0.31 | -1.016 |
| 6,5 | 0.378 | -1.414 |
| 7,0 | 0.41 | -1.725 |
| 7,5 | 0.429 | -1.98 |
| 8 | 0.446 | -2.209 |
| 8,5 | 0.465 | -2.432 |
| 9 | 0.482 | -2.66 |
| 9,5 | 0.495 | -2.898 |
| 10 | 0.5 | -3.142 |
Конструктивный расчет кольцевого направленного ответвителя.
Аналитический расчет ширин отрезков, эффективной диэлектрической проницаемости и длин отрезков
b
Рис.4
ε0, 0
a
ε=εrε0
0
Конструктивный расчет этих ответвителей сводится к определению геометрических длин отрезков линий и ширины полосковых проводников. Расчет геометрической длины, производимый с учетом относительной диэлектрической проницаемости εr или эффективной относительной диэлектрической проницаемости εэф (для случая квази-ТЕМ волн) материала платы, не требует пояснений.
Расчет ширины полоскового проводника производится по заданному волновому сопротивлению ρ. Для случая несимметричной (микрополосковой) линии (рис.4) волновое сопротивление вычисляется так :
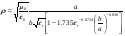
Эффективная относительная диэлектрическая проницаемость εэф для этого случая может быть вычислена по следующей формуле:
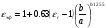 при b/a0.6
при b/a0.6 или
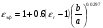 при b/a0.6
при b/a0.6 Численный расчет в пакете MWO (утилита TXLine)
Таблица 4.
| Волновое сопротивление, Ом | Ширина 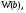 мм мм | Длина 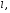 мм мм | Диэлектрическая проницаемость 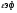 | Толщина пр-ков 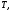 мм мм | Толщина мм | Рабочая частота 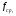 ГГЦ ГГЦ |
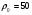 | 1.01594 | 8.7979 | 2.90282 | 0,05 | 0,5 | 5,0 |
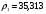 | 1.7496 | 8.56067 | 3.06596 | |||
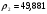 | 1.02005 | 8.79618 | 2.90398 |
Построение виртуальной модели кольцевого направленного ответвителя с помощью MWO.
Построение схемной модели направленного ответвителя и расчет комплексных коэффициентов передачи.
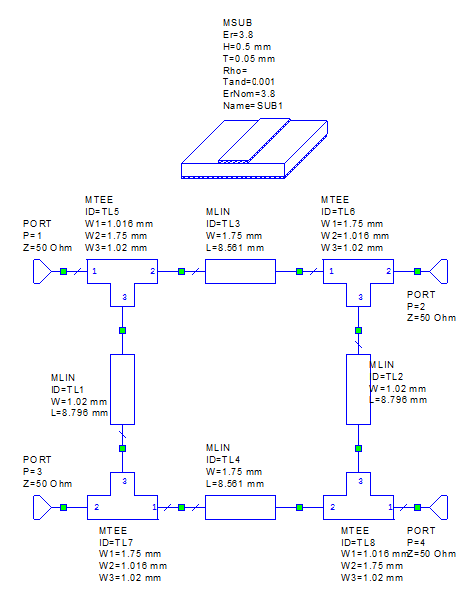
Рис.5. Схема квадратного шлейфного направленного ответвителя.
В результате моделирования схемы были получены следующие зависимости:
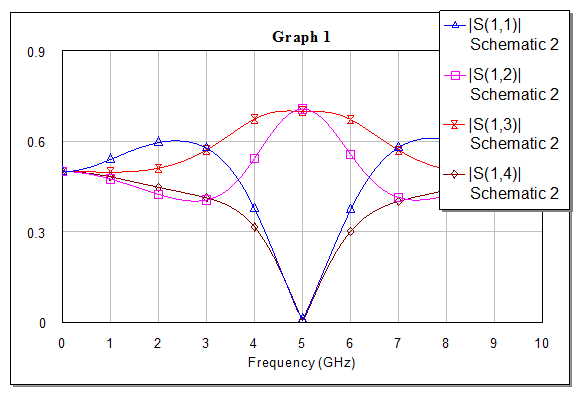
Рис.6. График зависимостей модулей коэффициентов матрицы рассеяния от частоты.
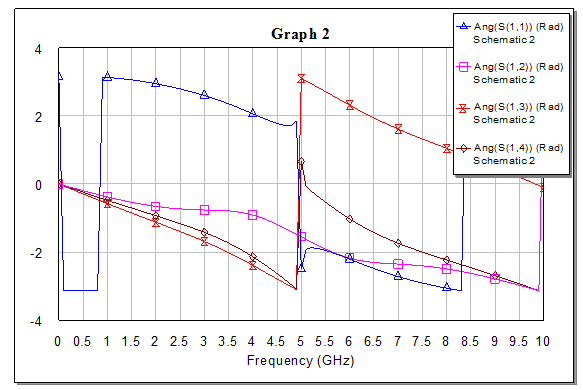
Рис.7. График зависимостей фаз коэффициентов матрицы рассеяния от частоты.
Таблица 5.
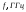 | 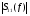 | 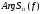 | 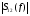 | 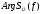 | 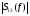 | 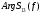 |
| 0,5 | 0.51153 | -3.1311 | 0.49293 | -0.19672 | 0.49997 | -0.29139 |
| 1,0 | 0.54098 | 3.1284 | 0.47386 | -0.37965 | 0.49891 | -0.57643 |
| 1,5 | 0.57402 | 3.0583 | 0.44764 | -0.53676 | 0.49817 | -0.85293 |
| 2,0 | 0.59791 | 2.9454 | 0.42068 | -0.65755 | 0.50114 | -1.1238 |
| 2,5 | 0.60278 | 2.7933 | 0.40133 | -0.73272 | 0.51217 | -1.3976 |
| 3,0 | 0.57787 | 2.5989 | 0.40346 | -0.76294 | 0.53547 | -1.6884 |
| 3,5 | 0.50717 | 2.3545 | 0.44852 | -0.79079 | 0.57391 | -2.0146 |
| 4,0 | 0.37324 | 2.0638 | 0.54744 | -0.91383 | 0.62544 | -2.3881 |
| 4,5 | 0.18596 | 1.7856 | 0.65923 | -1.1871 | 0.67508 | -2.7892 |
| 5,0 | 0.013647 | -2.557 | 0.70686 | -1.5522 | 0.69829 | -3.1042 |
| 5,5 | 0.19698 | -1.9568 | 0.65894 | -1.9123 | 0.69839 | 2.7152 |
| 6,0 | 0.37438 | -2.2128 | 0.55316 | -2.1775 | 0.69407 | 2.3151 |
| 6,5 | 0.50329 | -2.4866 | 0.46277 | -2.3044 | 0.66825 | 1.9412 |
| 7,0 | 0.5733 | -2.7218 | 0.42223 | -2.3527 | 0.61724 | 1.6135 |
| 7,5 | 0.59944 | -2.9117 | 0.4195 | -2.406 | 0.56473 | 1.3209 |
| 8 | 0.5964 | -3.0621 | 0.43543 | -2.4974 | 0.52557 | 1.045 |
| 8,5 | 0.57425 | 3.1077 | 0.45803 | -2.6278 | 0.50199 | 0.77125 |
| 9 | 0.54237 | 3.0355 | 0.47968 | -2.7904 | 0.49131 | 0.4903 |
| 9,5 | 0.51321 | 3.0088 | 0.4941 | -2.9768 | 0.48945 | 0.19852 |
| 10 | 0.50139 | 3.0169 | 0.4961 | 3.1079 | 0.49205 | -0.29139 |
Таблица 6.
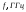 | 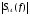 | 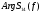 |
| 0,5 | 0.49495 | -0.24273 |
| 1,0 | 0.48208 | -0.47923 |
| 1,5 | 0.46481 | -0.70744 |
| 2,0 | 0.44665 | -0.93131 |
| 2,5 | 0.42914 | -1.162 |
| 3,0 | 0.40973 | -1.4196 |
| 3,5 | 0.3776 | -1.7335 |
| 4,0 | 0.30864 | -2.135 |
| 4,5 | 0.17759 | -2.6268 |
| 5,0 | 0.0028532 | 0.37293 |
| 5,5 | 0.18145 | -0.53863 |
| 6,0 | 0.3098 | -1.028 |
| 6,5 | 0.37649 | -1.4287 |
| 7,0 | 0.40683 | -1.7431 |
| 7,5 | 0.42484 | -2.0016 |
| 8 | 0.44146 | -2.2338 |
| 8,5 | 0.4594 | -2.4599 |
| 9 | 0.47726 | -2.692 |
| 9,5 | 0.49142 | -2.9349 |
| 10 | 0.49812 | 3.0971 |
Построение электродинамической модели направленного ответвителя.
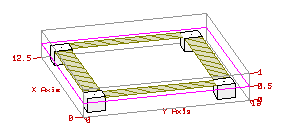

Рис.8. Электродинамическая модель направленного ответвителя.
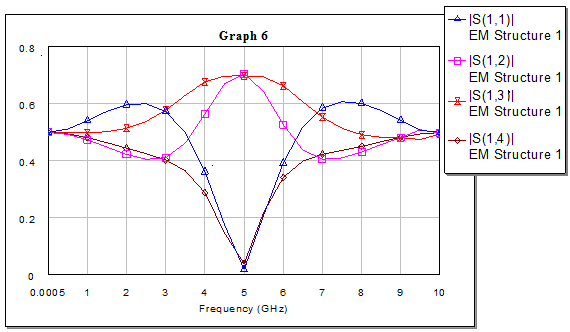
Рис.9. График зависимостей модулей коэффициентов матрицы рассеяния от частоты.
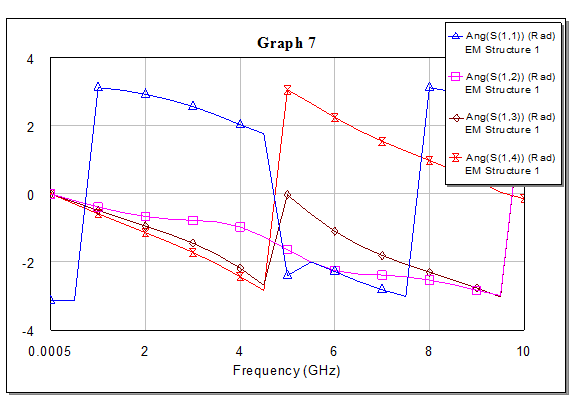
Рис.10. График зависимостей фаз коэффициентов матрицы рассеяния от частоты.
Таблица 7.
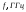 | 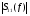 | 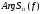 | 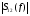 | 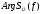 | 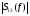 | 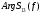 |
| 0,5 | 0,51155 | -3,1363 | 0,49296 | -0,19964 | 0,499 | -0,29492 |
| 1,0 | 0,54094 | 3,1177 | 0,47404 | -0,38503 | 0,49857 | -0,58332 |
| 1,5 | 0,5737 | 3,0418 | 0,44826 | -0,54409 | 0,50209 | -0,86348 |
| 2,0 | 0,59692 | 2,9227 | 0,42231 | -0,66631 | 0,51395 | -1,1386 |
| 2,5 | 0,60046 | 2,7642 | 0,40514 | -0,7432 | 0,53834 | -1,4176 |
| 3,0 | 0,57315 | 2,5634 | 0,41136 | -0,77896 | 0,57788 | -1,7153 |
| 3,5 | 0,49878 | 2,3143 | 0,46202 | -0,82224 | 0,62961 | -2,0499 |
| 4,0 | 0,36186 | 2,026 | 0,56369 | -0,96873 | 0,67715 | -2,4311 |
| 4,5 | 0,177 | 1,7676 | 0,6699 | -1,2612 | 0,69753 | -2,8357 |
| 5,0 | 0,018788 | 1,437 | 0,70566 | -1,6072 | 0,69848 | 3,0548 |
| 5,5 | 0,20851 | -1,9987 | 0,64333 | -2,0015 | 0,69462 | 2,6559 |
| 6,0 | 0,39215 | -2,2805 | 0,52729 | -2,2546 | 0,66362 | 2,2462 |
| 6,5 | 0,51968 | -2,5709 | 0,43829 | -2,3549 | 0,60724 | 1,8704 |
| 7,0 | 0,58524 | -2,8146 | 0,40562 | -2,3845 | 0,55285 | 1,5447 |
| 7,5 | 0,6073 | -3,01 | 0,41014 | -2,4345 | 0,51405 | 1,2537 |
| 8 | 0,60106 | 3,1174 | 0,43108 | -2,5301 | 0,49168 | 0,9774 |
| 8,5 | 0,57635 | 2,9981 | 0,45715 | -2,6657 | 0,48234 | 0,70028 |
| 9 | 0,54227 | 2,9175 | 0,48185 | -2,8307 | 0,48141 | 0,40997 |
| 9,5 | 0,50705 | 2,8486 | 0,50953 | -2,9875 | 0,47496 | 0,048387 |
| 10 | 0,50011 | 2,9171 | 0,49636 | 3,0317 | 0,49441 | -0,14481 |
Таблица 8.
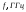 | 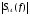 | 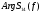 |
| 0,5 | 0,49481 | -0,24652 |
| 1,0 | 0,48152 | -0,48665 |
| 1,5 | 0,46357 | -0,71871 |
| 2,0 | 0,44437 | -0,94693 |
| 2,5 | 0,42519 | -1,183 |
| 3,0 | 0,40285 | -1,4474 |
| 3,5 | 0,36534 | -1,7701 |
| 4,0 | 0,2878 | -2,1808 |
| 4,5 | 0,14762 | -2,6804 |
| 5,0 | 0,038528 | 1,3904 |
| 5,5 | 0,21868 | -0,60154 |
| 6,0 | 0,34143 | -1,0983 |
| 6,5 | 0,39934 | -1,4994 |
| 7,0 | 0,42298 | -1,8114 |
| 7,5 | 0,43691 | -2,0684 |
| 8 | 0,45102 | -2,3011 |
| 8,5 | 0,46712 | -2,5297 |
| 9 | 0,48321 | -2,7666 |
| 9,5 | 0,4942 | -3,0269 |
| 10 | 0,4992 | 3,0217 |
Выводы.
В ходе выполнения курсовой работы был спроектирован направленный ответвитель, обладающий необходимыми свойствами. Анализ его параметров произведен несколькими способами, как аналитически, так и численно, в пакете программ Microwave Office. Использовались два разных подхода – схемный и электродинамический. Схожесть результатов, полученных данными способами, говорят о том, что расчет был произведен верно.
Были вычислены следующие параметры кольцевого направленного ответвителя:
При нахождении коэффициентов матрицы рассеяния, отклонение значений реального случая от идеализированного не превышало 2%.

 Задание на проектирование.
Задание на проектирование.