Вероятность 14. Закон больших чисел. Неравенства Маркова и Чебышева. Теорема Чебышева и ее обобщения. Теоремы Бернулли и Пуассона. Усиленный закон больших чисел Закон повторного логарифма. Центральная предельная теорема
 Скачать 332.5 Kb. Скачать 332.5 Kb.
|
ЛЕКЦИЯ 14Закон больших чисел. Неравенства Маркова и Чебышева. Теорема Чебышева и ее обобщения. Теоремы Бернулли и Пуассона. Усиленный закон больших чисел Закон повторного логарифма. Центральная предельная теорема. Теорема Ляпунова. Теорема Леви-Линдеберга. Теоремы Муавра-Лапласа. 11. ЗАКОН БОЛЬШИХ ЧИСЕЛПри изучении теории вероятностей приходится использовать понятия случайного события и случайной величины. При этом нельзя уверенно заранее предсказать результат испытания, в котором может появиться или не появится то или иное событие. Однако при неоднократном повторении испытаний могут наблюдаться определенные закономерности. Суть этих закономерностей заключается в свойстве устойчивости: некоторые характеристики случайных событий и случайных величин при неограниченном увеличении числа испытаний становятся практически не случайными. Например, любой газ состоит из огромного числа молекул, находящихся в непрерывном хаотическом движении (броуновском движении). Про каждую отдельную молекулу нельзя сказать, с какой скоростью она будет двигаться и в каком направлении. Однако основные характеристики газа – давление, температура, вязкость и др. – определяются не замысловатым поведением одной молекулы, а их совокупным действием. Так, давление газа равно суммарному воздействию молекул, ударившихся о пластину единичной площади в единицу времени. Число ударов и скорости ударившихся молекул меняются от случая к случаю, однако в силу "закона больших чисел" давление – величина постоянная, что подтверждается в физических экспериментах с очень большой точностью. В свое время это даже служило одним из аргументов против молекулярного строения вещества. Так называемые "флуктуации" давления газа удалось наблюдать только тогда, когда научились изолировать сравнительно небольшие количества молекул. Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к неслучайному результату. Эти условия указываются в теоремах, носящих название предельных. По смыслу их можно разбить на две группы, одна из которых называется законом больших чисел, а другая – центральной предельной теоремой. Под законом больших чисел не следует понимать какой-то один общий закон, связанный с большими числами. Закон больших чисел – это обобщенное название нескольких теорем, из которых следует, что при неограниченном увеличении числа испытаний средние величины стремятся к некоторым постоянным величинам. Другими словами, закон больших чисел – это общий принцип, в силу которого совместное действие случайных факторов приводит при весьма общих условиях к результату, почти не зависящему от случая. Теоремы закона больших чисел касаются вопросов приближения некоторых случайных величин к определенным предельным значениям, независимо от их закона распределения. Другая группа теорем, относящихся к центральной предельной теореме, устанавливают связь между законом распределения суммы случайных величин и нормальным распределением. Различные формы центральной предельной теоремы отличаются между собой условиями, накладываемые на сумму составляющих случайных величин. 11.1. Неравенство ЧебышеваНеравенство Маркова. Для любой случайной величины X, имеющей конечное абсолютное математическое ожидание и конечную дисперсию, при любом >0 имеет место неравенство: Доказательство. Ограничимся ДСВ. Пусть известен закон распределения случайной величины X. По отношению к числу возможные значения X разбиваются на две группы: одни не превосходят по модулю , а другие – больше . Предположим, что к первой группе относятся первые k значений случайной величины. Математическое ожидание случайной величины |X|: Так как члены этой суммы неотрицательны, то |xi|pi0, то отбрасывая первые k слагаемых, получим неравенство: Заменим оставшиеся значения xi меньшей величиной , от этого неравенство лишь усилится: Отсюда  . .Что и требовалось доказать. Следствие. Для любой случайной величины X, имеющей конечное число абсолютное математическое ожидание и конечную дисперсию, при любой >0 имеет место неравенство: Действительно, пусть Z=X2 – случайная величина, для которой выполняется неравенство X2>2. Применяя неравенство Маркова, получим Поскольку то Что и требовалось доказать. Пример 11.1. Измеряется скорость ветра в каком-то пункте Земли. Случайная величина X – проекция вектора скорости ветра на фиксированное направление. Оценить вероятность события A={|X|>25 м/с}, если путем многолетних наблюдений установлено, что: а) m=M[X]=5 м/с; б) =1 м/с. Решение. а) Воспользуемся неравенством б) Воспользуемся следствием из неравенства Маркова Неравенство Чебышева. Для любой случайной величины X, имеющей конечную дисперсию, при любом >0 имеет место неравенство: Действительно, применим следствие из неравенства Маркова для случайной величины |X–m|. Тогда Поскольку события |X–m|> и |X–m| противоположны, то Отсюда следует неравенство Чебышева. Отметим, что неравенство Чебышева справедливо для любых распределений случайной величины X. Оно ограничивает вероятность того, что случайная величина отклонится от своего математического ожидания на величину, более чем на . Из неравенства Чебышева следует, что при уменьшении дисперсии значения случайной величины с большей вероятностью сосредоточиваются около ее математического ожидания. Полагая =t, получим В частности, при t=1 имеем при t=2 имеем при t=3 имеем Замечание. Хотя неравенство Чебышева дает зачастую грубую, а иногда и тривиальную (см., что получилось выше при t=1) оценку вероятности, тем не менее значение его огромно. Выводы, получаемые отсюда, имеют фундаментальное теоретическое значение. Отметим также, что для некоторых распределений вместо неравенств можно получит точные равенства (см., например, тему: "Нормальное распределение"). Пример 11.2. Диаметр изготовляемых болтов представляет собой случайную величину, среднее значение (математическое ожидание) которой равно 20 мм. Среднее квадратичное отклонение, характеризующее погрешность изготовления болтов, равно 0,09 мм. Оценить вероятность того, что отклонение диаметра изготовленного болта от его среднего значения не превысит 0,5 мм. Решение. По условиям задачи имеем m=20 мм, =0,09 мм. Тогда Пример 11.3. Электростанция обслуживает сеть с 12000 лампами городского уличного освещения. Вероятность включения вечером каждой лампы равно 0,9. Оценить вероятность того, что число включенных вечером ламп будет отличаться от своего математического ожидания не более, чем на 100? Решение. Число включенных ламп есть величина случайная величина X, распределенная по биномиальному закону, где n=12000, p=0,9, q=0,1. Тогда M[X]=np=10800, D[X]=npq=1080. Воспользовавшись неравенством Чебышева, получим Отметим, что в данном случае можно найти точное значение, применив интегральную теорему Муавра-Лапласа: 11.2. Теорема ЧебышеваВведем новое понятие. Последовательность случайных величина {Xn} сходится по вероятности к числу a, если для любого сколь угодно малого числа >0 вероятность неравенства |Xn–a|с увеличением n стремится к единице: Подчеркнем различие между пределом, вводимым в математическом анализе, и пределом по вероятности. Если последовательность Xn стремится к a при n в смысле обычного анализа, то начиная с некоторого номера n для всех nN будет неуклонно выполняться неравенство |Xn–a|; если же Xn стремится к a при n по вероятности, то для отдельных значений n неравенство может и не выполняться. Теорема Чебышева. Пусть X1, X2, …, Xn– какая-либо последовательность независимых случайных величин и их дисперсии удовлетворяют условию Тогда для всех >0: где Другими словами, среднее арифметическое случайных величин при достаточно большом n сколь угодно мало (по вероятности) отклоняется от постоянной величины. Доказательство. Применим неравенство Чебышева к случайной величине Для этого необходимо найти ее математическое ожидание и дисперсию. В соответствии со свойствами математического ожидания, получим  . .В соответствии со свойствами дисперсии, получим  . .Таким образом, неравенство Чебышева для среднего арифметического независимых случайных величин будет иметь вид По условию, последнее слагаемое стремится к нулю при n. Поскольку вероятность не может быть больше единицы, то в итоге получается требуемый результат. Следствие 1. Пусть X1, X2, …, Xn – последовательность независимых случайных величин с равномерно ограниченными дисперсиями: D[Xn] Поскольку по условию все дисперсии равномерно ограничены, то неравенство (11.7) можно записать в виде Отсюда следует, что при n справедлив закон больших чисел (11.6). Следствие 2. Пусть X1, X2, …, Xn – последовательность независимых случайных величин, имеющие одинаковыематематические ожидания (равные a), а дисперсии удовлетворяют условиям теоремы Чебышева, то Данное следствие является наиболее простой формой закона больших чисел, применяемой на практике. Например, обычно для измерения некоторой физической величины производят несколько измерений и их среднее арифметическое принимают в качестве искомого значения. При каких условиях этот способ измерения можно считать правильным? Теорема Чебышева указывает условия, при которых указанный способ измерения может быть применен: 1) результаты измерений независимы от других измерений; 2) измерения проводятся без систематических ошибок (в этом случае математическое ожидание всех случайных величин одинаковы и равны истинному значению); 3) прибор обеспечивает определенную точность измерений (хотя при этом результаты отдельных измерений различны, но их рассеяние ограничено). На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого заключается в том, что по сравнительно небольшой случайной выборке судят о всей совокупности (генеральной совокупности) исследуемых объектов. Например, о качестве зерна судят по небольшой ее пробе. В этом случае число наудачу отобранных зерен мало по сравнению со всей массой зерна, но само по себе его достаточно велико. Пример 11.4. Для определения средней урожайности поля площадью 1800 га взяли в выборку по 1 м2 с каждого гектара. Известно, что по каждому гектару поля дисперсия не превышает 6 ц. Оценить вероятность того, что отклонение средней выборочной урожайности отличается от средней урожайности по всему полю не более чем на 0,25 ц. Решение. Воспользуемся неравенством (11.8), где =0,25, C=0,9, n=1800. Следовательно, Пример 11.5. Определить, сколько надо произвести замеров поперечного сечения деревьев на большом участке, чтобы средний диаметр деревьев отличался от истинного значения a не более чем на 2 см с вероятностью не меньшей 0,95. Среднее квадратичное отклонение поперечного сечения деревьев не превышает 10 см и измерения проводятся без погрешности. Решение. Будем считать выбор деревьев для замеров таким, что можно считать результаты измерений независимыми случайными величинами. Обозначим через Xi результаты измерения поперечного сечения i-го дерева. По условию задачи 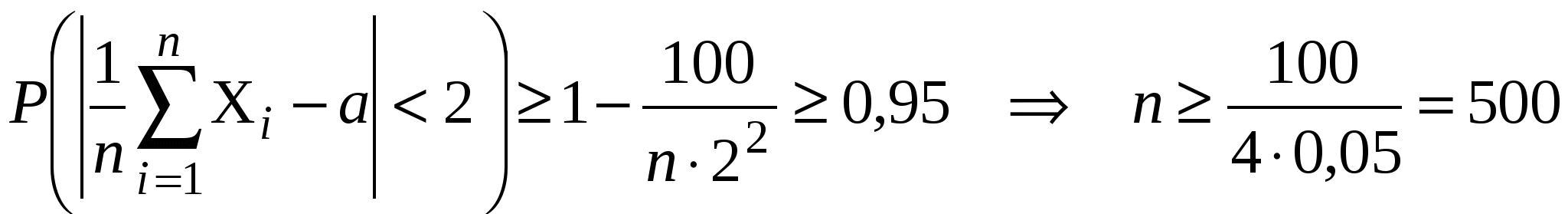 . .Итак, достаточно выполнить 500 замеров поперечного сечения деревьев. Заметим, что, вообще говоря, существование дисперсии является достаточным, но не является необходимым условием выполнения закона больших чисел. Примером этого может служить теорема Хинчина: для независимых одинаково распределенных Xn (или, как говорят, для независимых наблюдений над одной и той же случайной величиной X) закон больших чисел выполняется в любом случае, когда существует конечное математическое ожидание M[X]. Более того, существуют последовательности независимых одинаково распределенных случайных величин, даже не имеющих математического ожидания, но тем не менее удовлетворяющих закону больших чисел. Отметим, что для сумм независимых случайных величин можно сформулировать более или менее окончательный вид закона больших чисел. В частности, в теореме Колмогорова формулируются необходимые и достаточные условия того, чтобы последовательность взаимно независимых случайных величин подчинялась закону больших чисел. Пример 11.6*. Последовательность независимых случайных величин X1, X2, …, Xn, … задана законом распределения
Применим ли к заданной последовательности теорема Чебышева? Решение. Здесь достаточно показать, что для данных независимых случайных величин их дисперсии равномерно ограничены. Вычислим дисперсии Предположим, что n изменяется непрерывно и исследуем на экстремум функцию Историческая справка. Впервые доказал и сформулировал одну из теорем закона больших чисел швейцарский математик Я. Бернулли (1654-1705). Эта теорема была опубликована в его книге "Искусство предположений" (1713) и является одной из простейших форм закона больших чисел. Теорема Бернулли получила свое первое обобщение лишь в 1837 г. в работе французского математика С. Пуассона (1781-1846): "Исследования о вероятностях суждений". Именно в этом сочинении появился термин "закон больших чисел". Существенный сдвиг в развитии закона больших чисел связан с работой П.Л. Чебышева (1821-1894) "О средних величинах" (1867). В этой работе он перешел от рассмотрения случайных событий к случайным величинам и получил знаменитые неравенства и теоремы, названные впоследствии его именем. Дальнейшие усилия обобщения теоремы Чебышева долго не приносили принципиальных успехов. Лишь в 1907 г. А.А. Марков (1856-1922) нашел условия, обобщающие теорему Чебышева на случай зависимых величин, а 1923 г. А.Я. Хинчин (1894-1959) показал, что если случайные величины не только независимы, но и одинаково распределены, то существование математического ожидания является достаточным условием для применимости закона больших чисел. Принципиальный результат был получен лишь в 1926 г. А.Н. Колмогоровым (1903-1987), который сформулировал о необходимые и достаточные условия для того, чтобы последовательность взаимно независимых случайных величин подчинялась закону больших чисел. Дальнейшие усилия ученых по углублению содержания закона больших чисел были направлены на получение наиболее общих условий применимости этого закона к последовательности зависимых случайных величин. Для практики исключительно важно выяснить вопрос о применимости закона больших чисел именно к зависимым случайным величинам, т.к. явления в природе и обществе находятся во взаимной зависимости. Впервые соответствующие теоремы были доказаны А.А. Марковым в 1907 г. Теорема Маркова. Если последовательность случайных величин X1, X2, …, Xn такова, что то каково бы ни было положительное число выполняется где Доказательство теоремы Маркова является следствием неравенства Чебышева (докажите самостоятельно). Очевидно, также, что теорема Чебышева является частным случаем теоремы Маркова. Задача. Покажите, что для последовательности случайных величин (в общем случае, зависимых), рассмотренной в примере 11.6, применима теорема Маркова. В общем случае, применимость закона больших чисел к суммам зависимых величин в первую очередь связана с неограниченным убыванием зависимости между случайными величинами Xi и Xj при увеличении разности их номеров, т.е. |i–j|. Соответствующие теоремы для случайных величин связанных в цепь также были рассмотрены А.А. Марковым. Основной результат этих работ заключается в том, что закон больших чисел приложим к зависимым случайным величинам, если только сильная зависимость существует между случайными величинами с близкими номерами, а с далекими номерами зависимость достаточно слаба. Например, на погоду каждого дня заметно влияет погода предыдущих дней, причем влияние заметно ослабевает с удалением дней друг от друга. Следовательно, многолетняя средняя температура, давление и другие характеристики климата данной местности в соответствии с законом больших чисел практически должны быть близки к своим математическим ожиданиям и являются объективными характеристиками климата местности. Отметим, что более общие условия были рассмотрены С.Н. Бернштейном (1880-1868) в 1946 г. 11.3. Теорема БернуллиПусть производится n независимых испытаний, в каждом из которых вероятность появления события A равна p. Можно ли предвидеть, какова примерно будет относительная частота появлений события A? Положительный ответ на этот вопрос дает теорема Бернулли. Историческая справка. Эта теорема была опубликована Я. Бернулли в 1713 г. Однако доказательство Бернулли было очень сложным. Более простое доказательство теоремы дал П.Л. Чебышев в 1846 г. В 1837 г. С. Пуассон доказал аналогичную теорему в более широких условиях. Теорема Бернулли. Если в каждом из n независимых испытаний вероятность p появления события A постоянна, то при достаточно большом числе испытаний отклонение относительной частоты от вероятности p будет сколь угодно малым Доказательство. Рассмотрим в качестве случайной величины Xi число появлений события A в i-ом испытании. Каждая из этих величин может принимать только два значения: 1 с вероятностью p и 0 – с вероятностью q. Математическое ожидание и дисперсия этих величин равны Поскольку дисперсии всех этих величин Xi ограничены pq1/4 (доказать самостоятельно) и, кроме того, случайные величины независимы, то применяя к случайной величине Поскольку Отсюда при n получаем утверждение теоремы Бернулли (11.12). Пример 11.7. При штамповке пластинок из пластмассы брак составляет 3%. Найти вероятность того, что при проверке партии в 1000 пластинок выявится отклонение от установленного процента брака меньше чем на 1%. Решение. Из условия задачи следует, что n=1000, =0,01, p=0,03, q=1–p=0,97. В соответствии с формулой (11.13), получим Пример 11.8. При каком числе независимых испытаний вероятность выполнения неравенства Решение. По условию задачи имеем: =0,2, p=0,7, q=0,3. Условие P>0,96 равносильно неравенству Следовательно, требуемое неравенство выполняется при числе независимых испытаний, начиная со 132. Теорема Бернулли устанавливает связь между вероятностью появления события и его относительной частотой появления и позволяет предсказать, какой будет примерно эта частота в n испытаниях. Из теоремы Бернулли видно, что относительная частота На практике сравнительно редко вероятность наступления события во всех испытаниях остается одной и той же. Чаще всего она меняется от испытания к испытанию. К схеме испытаний такого типа относится теорема Пуассона. Теорема Пуассона. Если в последовательностинезависимых испытаний вероятность появления события A в i-м испытании равна pi, то где Доказательство. Рассмотрим в качестве случайной величины Xi число появлений события A в i-ом испытании. Каждая из этих величин может принимать только два значения: 1 с вероятностью pi и 0 – с вероятностью qi. Математическое ожидание и дисперсия этих величин равны Тогда неравенство Чебышева для относительной частоты появлений событий (11.13) примет вид Отсюда при n получаем утверждение теоремы Пуассона (11.14). Пример 11.9. Проведено 800 независимых испытаний: в 200 из них вероятность появления ожидаемого результата была 0,5, в 400 испытаниях эта вероятность была 0,4, и, наконец, в оставшихся случаях вероятность благоприятствующего исхода была равна 0,3. Оценить вероятность того, что отклонение относительной частоты появления ожидаемого результата от средней вероятности по абсолютной величине не превысит 0,04. Решение. Найдем среднюю вероятность наступления события в 800 испытаниях: Таким образом, в задаче требуется оценить вероятность Более точная оценка будет иметь следующий вид  11.4*. Усиленный закон больших чисел. |

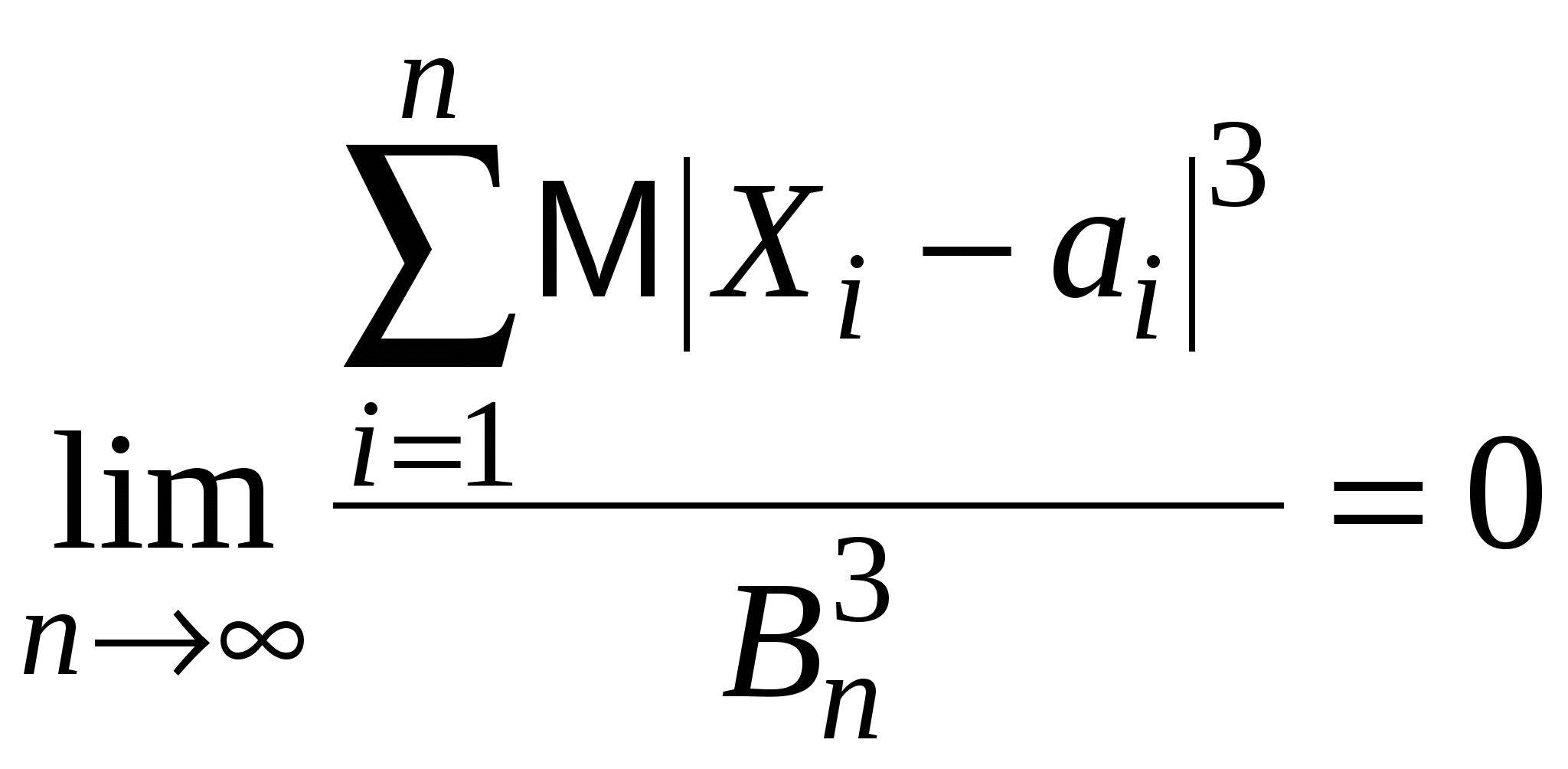 ,
,
 имеет стандартное нормальное распределение. Так как
имеет стандартное нормальное распределение. Так как