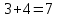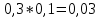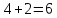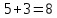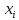Теория вероятности. Решение. Искомую вероятность найдем по формуле Бернулли Ответ 0,0081
 Скачать 63.44 Kb. Скачать 63.44 Kb.
|
|
Вариант 1. 1. Найти вероятность того, что среди взятых наудачу пяти деталей две стандартные, если вероятность того, что каждая деталь окажется стандартной, равна 0,9. Решение.   Искомую вероятность найдем по формуле Бернулли: 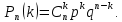   Ответ: 0,0081. 2. Команда состоит из двух стрелков. Числа очков, выбиваемых каждым из них при одном выстреле, являются случайными величинами  и и  , которые характеризуются следующими законами распределения: , которые характеризуются следующими законами распределения:
Результаты стрельбы одного стрелка не влияют на результаты стрельбы второго. Составить закон распределения числа очков, выбиваемых данной командой, если стрелки сделают по одному выстрелу. Найдём закон распределения случайной величины  . .Заполним расчетную таблицу:
В случае совпадения некоторых сумм соответствующие вероятности складываются:   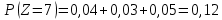   Таким образом, закон распределения случайной величины  примет вид: примет вид:
Убеждаемся в том, что сумма вероятностей всех возможных исходов равна единице. Действительно, 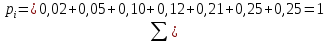 Ответ:
Вариант 2. 1. В магазин поступает продукция трех фабрик. Причем продукция первой фабрики составляет 20%, второй – 45% и третьей – 35% изделий. Известно, что средний процент нестандартных изделий для первой фабрики равен 3%, для второй – 2%, и для третьей – 4%. Чему равна вероятность того, что оказавшееся нестандартным изделие произведено на ПЕРВОЙ фабрике? Решение.  продукция поступила с первой фабрики. продукция поступила с первой фабрики.   продукция поступила со второй фабрики. продукция поступила со второй фабрики. 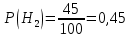  продукция поступила с третьей фабрики. продукция поступила с третьей фабрики.  изделие оказалось нестандартным. изделие оказалось нестандартным.Условные вероятности этого события равны: 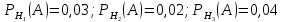 По формуле полной вероятности имеем:  ; ;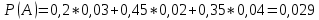 Вероятность того, что оказавшееся нестандартным изделие произведено на первой фабрике, найдем по формуле Байеса: 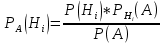  Ответ: 0,2069. 2. Найти дисперсию случайной величины  , имеющей следующий закон распределения , имеющей следующий закон распределения
Решение. Математическое ожидание:   Дисперсия:  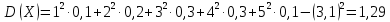 Ответ:  Вариант 3. 1. Завод изготовил две партии автомобилей. Первая партия в три раза больше второй. Надежность автомобилей первой партии 0,9, второй 0,8. Определить вероятность того, что наугад купленный автомобиль будет надежным. Решение. Пусть 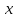 автомобилей изготовлено второй партией, тогда первой партией изготовлено автомобилей изготовлено второй партией, тогда первой партией изготовлено  автомобилей. автомобилей.  автомобиль изготовлен первой партией. автомобиль изготовлен первой партией. 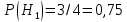  автомобиль изготовлен второй партией. автомобиль изготовлен второй партией.   купленный автомобиль будет надежным. купленный автомобиль будет надежным.Условные вероятности этого события равны:  По формуле полной вероятности имеем:  ; ; Ответ: 0,875. 2. График функции распределения случайной величины имеет вид:  Найти 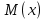 . .Решение. Найдем функцию распределения  . .При  При  график проходит через точки график проходит через точки  и и  . .Уравнение прямой, проходящее через 2 точки  , имеет вид: , имеет вид: Подставляя в него координаты точек  и и  , получаем: , получаем: Таким образом, при 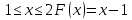 При  Функция распределения примет вид:  Плотность распределения  : : Математическое ожидание:  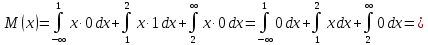 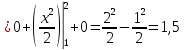 Ответ:  . .Вариант 4. 1. В урне 9 белых и 6 черных шаров. Из урны вынимают два шара. Какова вероятность того, что оба шара окажутся белыми? Решение. Применим классическое определение вероятности:   число благоприятных исходов; число благоприятных исходов;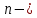 число всевозможных исходов; число всевозможных исходов;Всего имеется 15 шаров (9 белых и 6 черных), из них вынимают два    оба вынутых шара окажутся белыми. оба вынутых шара окажутся белыми.  Ответ: 0,3429. 2. В студенческой группе организована лотерея. Разыгрываются две вещи стоимостью по 1000 руб. и одна стоимостью 3000 руб. Составить закон распределения суммы чистого выигрыша для студента, который приобрел один билет за 100 руб.; всего продано 50 билетов. Решение. Случайная величина  сумма чистого выигрыша, может принимать три значения: - 100 руб. (если студент не выиграет, а фактически проиграет 100 руб., уплаченные им за билет), 900 руб. и 2900 руб. (фактический выигрыш уменьшается на 100 руб. - на стоимость билета). Первому результату благоприятствуют 47 случаев из 50, второму - 2, а третьему - один. Поэтому их вероятности таковы: сумма чистого выигрыша, может принимать три значения: - 100 руб. (если студент не выиграет, а фактически проиграет 100 руб., уплаченные им за билет), 900 руб. и 2900 руб. (фактический выигрыш уменьшается на 100 руб. - на стоимость билета). Первому результату благоприятствуют 47 случаев из 50, второму - 2, а третьему - один. Поэтому их вероятности таковы:   Закон распределения примет вид:
Ответ:
Вариант 5. 1. Завод изготовил две партии телевизоров. Первая партия телевизоров в два раза больше второй. Надежность телевизоров первой партии – 0,9, второй партии – 0,8. Определить вероятность того, что наугад купленный телевизор будет надежным. Решение. Пусть 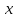 телевизоров изготовлено второй партией, тогда первой партией изготовлено телевизоров изготовлено второй партией, тогда первой партией изготовлено  телевизоров. телевизоров.  телевизор изготовлен первой партией. телевизор изготовлен первой партией. 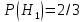  телевизор изготовлен второй партией. телевизор изготовлен второй партией.   купленный телевизор будет надежным. купленный телевизор будет надежным.Условные вероятности этого события равны:  По формуле полной вероятности имеем:  ; ;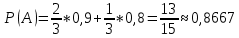 Ответ: 0,8667. 2. В парке отдыха организована беспроигрышная лотерея. Имеется 1000 выигрышей, из них 400 – по 100 руб.; 300 – по 200 руб.; 200 – по 1000 руб. и 100 – по 2000 руб. Какой средний размер выигрыша для посетителя парка, купившего один билет? Решение. Случайная величина  размер выигрыша, может принимать четыре значения: 100, 200, 1000, 2000 р. Первому результату благоприятствуют 400 случаев из 1000, второму - 300, третьему – 200 и четвертому 100. Поэтому их вероятности таковы: размер выигрыша, может принимать четыре значения: 100, 200, 1000, 2000 р. Первому результату благоприятствуют 400 случаев из 1000, второму - 300, третьему – 200 и четвертому 100. Поэтому их вероятности таковы:    Закон распределения примет вид:
Математическое ожидание:   Ответ: средний размер выигрыша для посетителя парка, купившего один билет, составит 500 рублей. 1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. Изд. 4-е, стер. М.: Высш. шк., 1997. – 400 с.: ил. 2. Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. Изд. 6-е, стер. – М.: Высш. шк., 1997. – 479 с.: ил. 3. Гнеденко Б.В. Курс теории вероятностей: Учебник – Изд. 6-е, перераб. и доп. – М.: Наука. Гл. ред. физ. –мат. лит., 1988. – 448 с. |