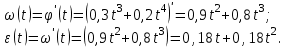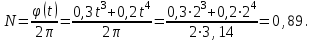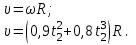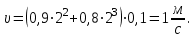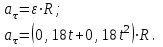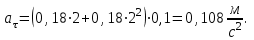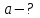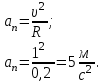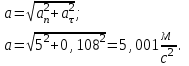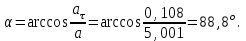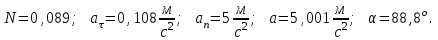Задача 1
Задан закон движения 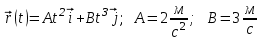 материальной точки в координатной плоскости ху винтервале времени от материальной точки в координатной плоскости ху винтервале времени от  до до  . Найти уравнение траектории . Найти уравнение траектории  и построить график. Найти модуль вектора перемещения точки в заданном интервале времени. Найти модуль начальной и построить график. Найти модуль вектора перемещения точки в заданном интервале времени. Найти модуль начальной  и конечной и конечной  скорости точки. скорости точки.
Дано:
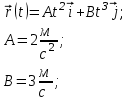
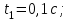
 . .
|
Решение:
Представим уравнение траектории в параметрическом виде:
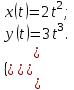
С первого уравнения находим время и подставляем во второе уравнение:
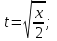

Вычисляем координаты точки в моменты времени 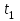 и и 

Вычисляем модуль вектора перемещения точки в заданном интервале времени по формуле:
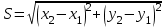 . .
Подставим значения и вычислим:

Учитывая, что скорость материальной точки это производная координаты
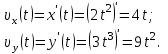
|
Найти:
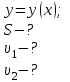
|
Вычисляем координаты векторов скорости точки в моменты времени 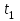 и и 
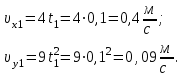 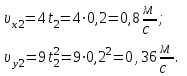
Тогда модуль начальной скорости:
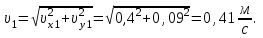
Модуль конечной скорости:

Ответ:  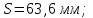 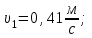 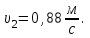
|
Задача 2
Частица движется равноускоренно в координатной плоскости ху с начальной скоростью 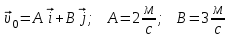 и ускорением и ускорением 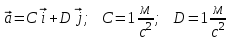 . Найти модули векторов скорости . Найти модули векторов скорости 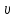 , тангенциального , тангенциального  и нормального и нормального 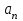 ускорений, а также радиус кривизны R траектории в момент времени ускорений, а также радиус кривизны R траектории в момент времени 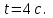
Дано:
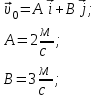
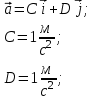
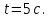
|
Решение:
Запишем координаты вектора начальной скорости:
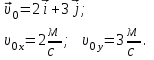
Запишем координаты вектора ускорения:

Следовательно, в направлении оси х движении равноускоренно и в направлении оси у равноускоренно.
Запишем уравнение траектории частицы в параметрическом виде.
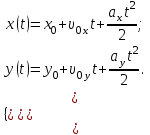
За начало координат принимаем точку с координатами 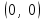 . После подстановки соответственных значений, получаем: . После подстановки соответственных значений, получаем:
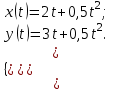
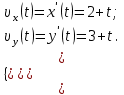
Для момента времени  , получаем: , получаем:
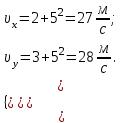
Тогда модуль вектора скорости будет:

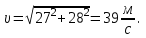
Вычисляем полное ускорение по формуле:
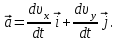
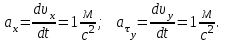
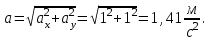
Тангенс угла, который образует касательная к траектории в момент времени 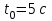 , вычисляется по формуле: , вычисляется по формуле:

Тогда
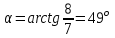 . .
Согласно рисунку 2:
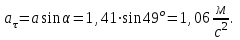
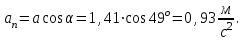
Нормальное ускорение вычисляется по формуле:
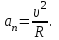
Откуда

Ответ: 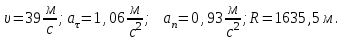
|
Найти:
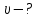

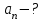
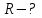
|
Задача 3
Частица движется по окружности радиуса 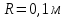 . Угол поворота радиус – вектора частицы меняется со временем по закону . Угол поворота радиус – вектора частицы меняется со временем по закону 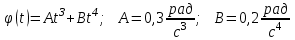 . Найти число оборотов . Найти число оборотов  , которые частица совершает в интервале времени от , которые частица совершает в интервале времени от 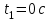 до до 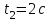 . Найти модули векторов тангенциального . Найти модули векторов тангенциального  , нормального , нормального 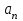 и полного и полного 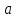 ускорений, а также угол ускорений, а также угол 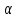 между векторами тангенциального и полного ускорений в момент времени между векторами тангенциального и полного ускорений в момент времени  . .
Дано:
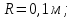 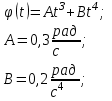
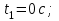

|
Решение:
Учитывая закон движения частицы по окружности 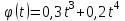 находим угловую скорость находим угловую скорость 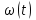 и угловое ускорение и угловое ускорение 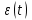 частицы: частицы:
 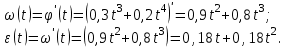
Вычисляем количество оборотов:
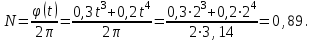
Вычислим линейную скорость точки в момент времени 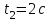 , по формуле: , по формуле:
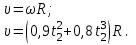
Подставим численные значения и вычислим:
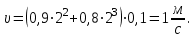
Вычисляем тангенциальное ускорение в момент времени 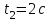 , по формуле: , по формуле:
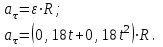
Подставим численные значения и вычислим:
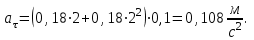
Вычисляем нормальное ускорение в момент времени 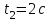 , по формуле: , по формуле:
|
Найти:


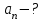
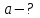
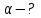
|
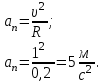
Вычисляем полное ускорение:
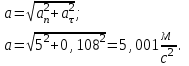
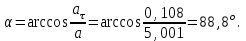
Ответ: 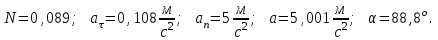
| |
 Скачать 147.98 Kb.
Скачать 147.98 Kb.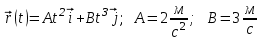 материальной точки в координатной плоскости ху винтервале времени от
материальной точки в координатной плоскости ху винтервале времени от  до
до  . Найти уравнение траектории
. Найти уравнение траектории 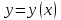 и построить график. Найти модуль вектора перемещения точки в заданном интервале времени. Найти модуль начальной
и построить график. Найти модуль вектора перемещения точки в заданном интервале времени. Найти модуль начальной 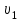 и конечной
и конечной  скорости точки.
скорости точки.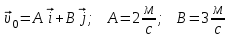 и ускорением
и ускорением 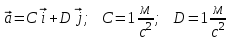 . Найти модули векторов скорости
. Найти модули векторов скорости 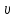 , тангенциального
, тангенциального  и нормального
и нормального 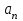 ускорений, а также радиус кривизны R траектории в момент времени
ускорений, а также радиус кривизны R траектории в момент времени 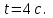
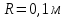 . Угол поворота радиус – вектора частицы меняется со временем по закону
. Угол поворота радиус – вектора частицы меняется со временем по закону 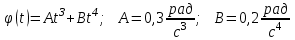 . Найти число оборотов
. Найти число оборотов 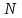 , которые частица совершает в интервале времени от
, которые частица совершает в интервале времени от 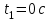 до
до 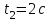 . Найти модули векторов тангенциального
. Найти модули векторов тангенциального  , нормального
, нормального 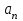 и полного
и полного 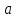 ускорений, а также угол
ускорений, а также угол 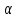 между векторами тангенциального и полного ускорений в момент времени
между векторами тангенциального и полного ускорений в момент времени  .
.
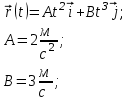
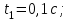
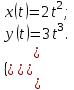
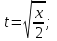

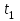 и
и 

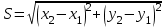 .
.
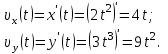
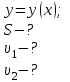
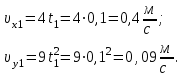
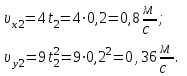
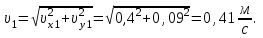


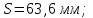
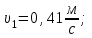
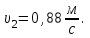
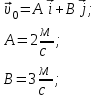
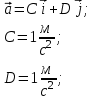
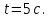
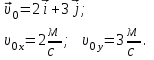

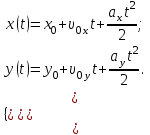
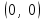 . После подстановки соответственных значений, получаем:
. После подстановки соответственных значений, получаем: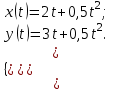
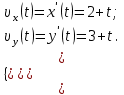
 , получаем:
, получаем: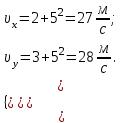

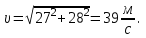
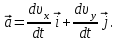
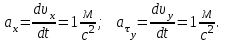
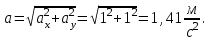
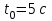 , вычисляется по формуле:
, вычисляется по формуле:
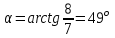 .
.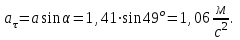
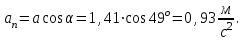
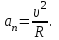

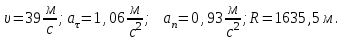
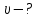

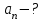
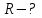
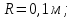
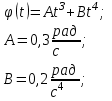
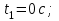

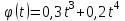 находим угловую скорость
находим угловую скорость  и угловое ускорение
и угловое ускорение 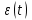 частицы:
частицы: