Физика. Изучение з. Стефана -Больцмана. Законы теплового излучения

• Название: Законы теплового излучения
• Анкор: Физика
• Дата: 02.06.2021
• Размер: 304.5 Kb.
• Имя файла: Изучение з. Стефана -Больцмана .doc
• Тип: Закон; #213245

ЗАКОНЫ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
Излучение, испускаемое нагретыми телами, называется тепловым. Тепловое излучение по своей природе является электромагнитным и происходит за счёт изменения внутренней энергии вещества, оно свойственно всем телам, имеющим температуру, отличную от абсолютного нуля (шкала Кельвина). Тепловое излучение ведёт к уменьшению внутренней энергии тела, а следовательно, к понижению его температуры, т. е. к охлаждению. Человек тепловое излучение воспринимает как тепло и свет.

Постоянное испускание и поглощение энергии телом приводит к тому, что в изолированной системе установится температура, при которой тело в единицу времени будет поглощать столько же энергии, сколько и излучать, а спектр излучаемой и поглощаемой энергии остаётся неизменным по времени. Излучение такого типа называется равновесным. Тепловое излучение – это единственный вид излучения, который может быть равновесным. Для теплового излучения состояние термодинамического равновесия изолированной системы устанавливается с течением времени. Если система достигла термодинамического равновесия и внешние условия не меняются, то система не может сама произвольно выйти из этого состояния. К равновесным состояниям и процессам применимы законы термодинамики, поэтому тепловое излучение подчиняется общим закономерностям, вытекающим из принципов термодинамики.

Для количественной оценки способности каждого тела испускать или поглощать энергию при некоторой температуре вводятся следующие понятия:

1. Энергетическая светимость R_э – это величина лучистого потока Ф, излучаемого единицей поверхности тела s в единицу времени t:

(1)

Энергетическая светимость в общем случае является функцией температуры и спектрального состава излучения.

2. Спектральная плотность энергетической светимости тела – это мощность излучения с единицы площади поверхности тела в единичном интервале частот:

(2)

где – энергия электромагнитного излучения, испускаемого в единицу времени (мощность излучения) с единицы поверхности тела в интервале частот от до ,

или

(3)

Записанную формулу можно представить также в виде функции длины волны:

(4)

так как

,

то

(5)

знак «–» означает, что с увеличением длины волны частота убывает, и наоборот. В дальнейшем знак «–» не будем учитывать, следовательно:

(6)

Эта формула позволяет перейти от значения к , и наоборот.

Спектральная плотность энергетической светимости связана с энергетической светимостью тела соотношением

(7)

или

(8)

Так как длины волн электромагнитного излучения меняются в пределах от нуля до бесконечности, то интегральная энергетическая светимость или просто энергетическая светимость тела равна:

(9)

или

(10)

Вид спектральной характеристики теплового излучения 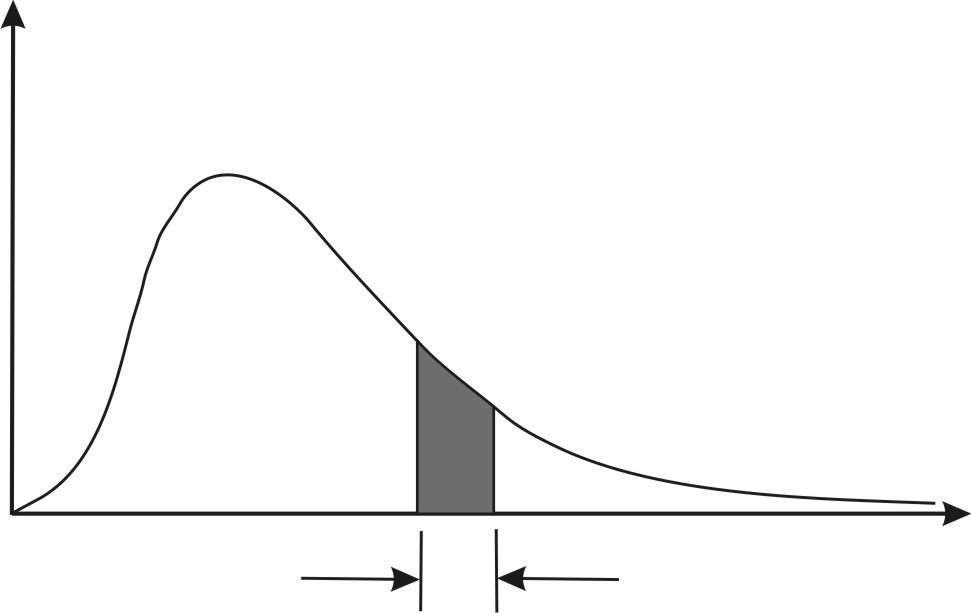для некоторой температуры T показан на рис. 6.1, где заштрихованная площадь соответствует энергетической светимости R_э, а площадь крестообразной штриховки соответствует части энергетической светимости, приходящейся на интервал длин волн .


r_{λ, Т}

λ

dλ


Рис. 6.1

3. Спектральная поглощательная способность 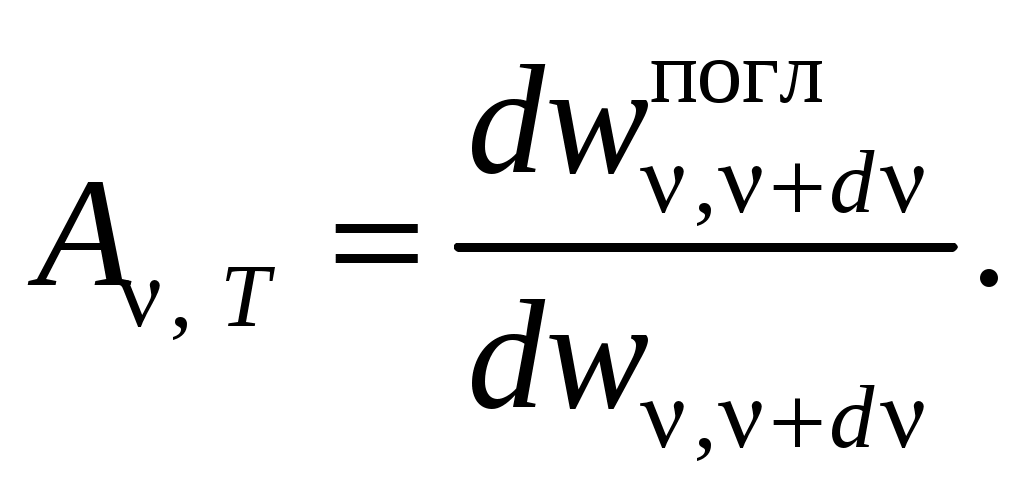показывает, какая доля энергии, падающей в единицу времени на единицу площади поверхности тела в интервале частот от до поглощается этим телом:

(11)

Спектральная поглощательная способность зависит от материала тела и состояния его поверхности.

Тело, которое при любой температуре полностью поглощает всю энергию падающего на него света любой частоты, называется абсолютно чёрным телом.

Для абсолютно чёрного тела . В природе абсолютно черного тела нет, однако такие тела, как сажа, чёрный бархат, чёрная бумага и другие, в определённом интервале частот от до по свойствам близки к ним.

Простейшей моделью абсолютно черного тела может служить замкнутая полость с непроницаемыми стенками и малым выходным отверстием (рис. 2). Луч света, попавший внутрь такой полости, испытывает многократные отражения от стенок, в результате чего интенсивность вышедшего излучения практически равна нулю.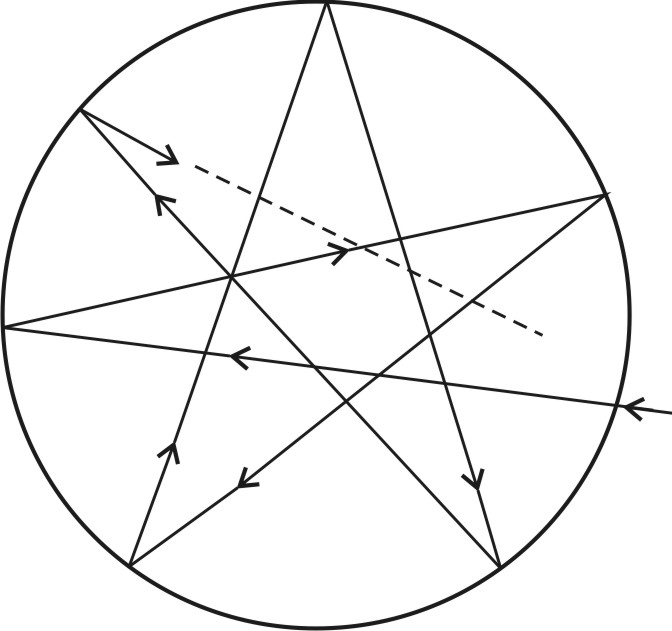


Рис. 6.2

О


Н
Рис. 6.2
аряду с понятием абсолютно черного тела используют понятие серого тела – тела, поглощательная способность которого меньше единицы, но одинакова для всех частот и зависит только от температуры тела и состояния его поверхности.

.

В 1859 г. Кирхгоф установил закон, который формулируется следующим образом: отношение спектральной плотности энергетической светимости тела к его поглощательной не зависит от природы тела, оно является для всех тел одной и той же универсальной функцией частоты (длины волны) и температуры.

(12)

Для абсолютно черного тела , следовательно, из закона Кирхгофа вытекает, что или .

Таким образом, универсальная функция Кирхгофа есть спектральная плотность энергетической светимости чёрного тела при такой же температуре и частоте. Из закона Кирхгофа следует, что спектральная плотность энергетической светимости любого тела в любой области спектра всегда меньше спектральной плотности энергетической светимости абсолютно черного тела (при тех же значениях 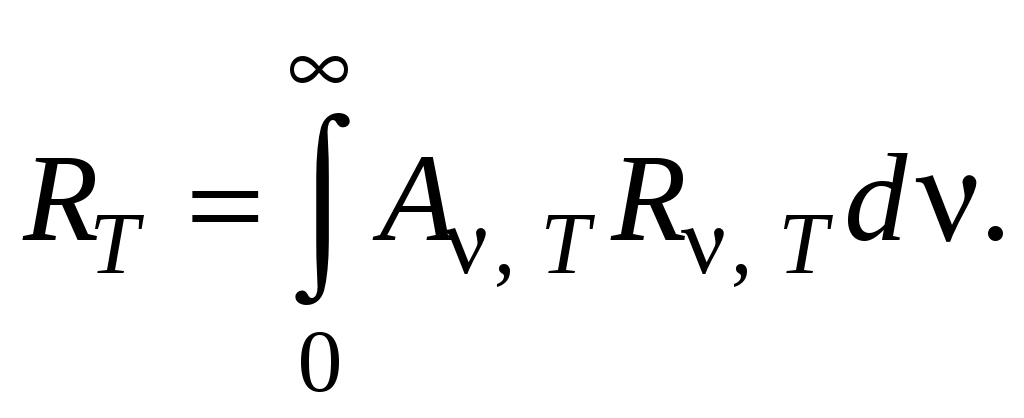и ), так как . Следовательно, . Согласно закону Кирхгофа:

(13)

Теоретическое объяснение излучения абсолютно черного тела (рис. 6.3) и его законов имело огромное значение в развитии физики – оно привело к понятию квантов энергии. Главной задачей теории теплового излучении было нахождение функции f(λ,T). В 1879 г. из анализа экспериментальных данных австрийский учёный И. Стефан пришёл к выводу, что энергетическая светимость R_Т любого тела пропорциональна четвёртой степени абсолютной температуры, а в 1884 г. Л. Больцман теоретически показал, что выводы Стефана применимы только для абсолютно черного тела:

(14)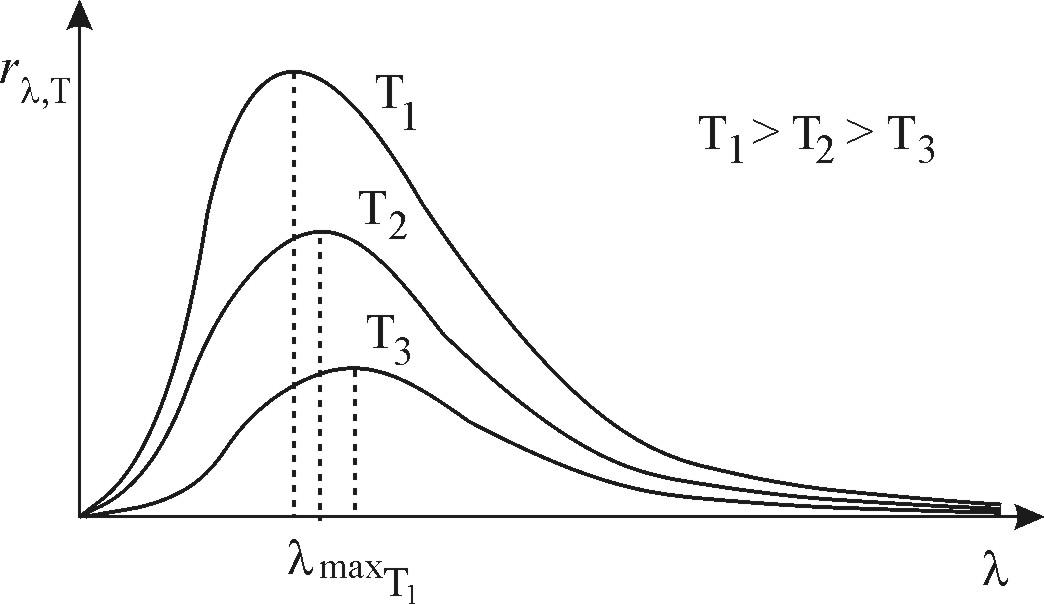


r_{λ, Т}

Т₂

Т₁

Т₃

Т₁ > Т₂ > Т₃

λ_maxТ1


Рис. 3

Энергетическая светимость абсолютно черного тела пропорциональна четвёртой степени абсолютной температуры – закон Стефана – Больцмана:

(15)

где Вт(м^–2∙К^–4) – постоянная Стефана – Больцмана.

Так как нагретое тело состоит из большого количества атомов, каждый из которых является источником электромагнитного излучения определённой частоты, то излучение нагретого тела содержит всевозможные частоты, а следовательно, и длины волн. Распределение энергии излучения абсолютно черного тела по длинам волн было изучено опытным путём, в результате чего были получены кривые распределения энергии излучения абсолютно черного тела по длинам волн при различных температурах.

Площадь, ограниченная каждой кривой и осью абсцисс, определяет полную энергию всевозможных длин волн, испускаемую единицей площади поверхности абсолютно черного тела в единицу времени. Все кривые имеют максимум, причём с увеличением температуры большая часть энергии приходится на более короткие волны. Для каждой температуры существует такая длина волны , на которую приходится наибольшая часть энергии, испускаемой абсолютно черным телом.

При повышении температуры длина волны становится всё более короткой. Именно поэтому раскалённое тело с повышением температуры становится сначала красным, затем оранжевым и, наконец, жёлто-белым. Экспериментальные кривые, которые исследовал немецкий учёный Вин в 1893 г., позволили сделать вывод: длина волны, на которую приходится максимум спектральной плотности энергетической светимости абсолютно черного тела, связана с абсолютной температурой соотношением

(16)

или

(17)

где мК.

Это соотношение получило название первого закона Вина: длина волны, на которую приходится максимум спектральной плотности энергетической светимости излучения абсолютно черного тела, обратно пропорциональна абсолютной температуре. Величина же максимума спектральной плотности энергетической светимости пропорциональна пятой степени абсолютной температуры. Это второй закон Вина:

(18)

где Дж/м³сК⁵.

Контрольные вопросы и задания

1. Какова природа теплового излучения?

2. Что такое абсолютно черное тело?

3. Дайте понятие энергетической светимости.

4. Что такое спектральная плотность энергетической светимости тела?

5. Что показывает спектральная поглощательная способность тела?

6. Сформулируйте законы смещения Вина.

7. Сформулируйте закон Стефана – Больцмана.

8. Сформулируйте закон Кирхгофа.

9. Что такое серое тело?

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

Основная литература

1. Трофимова, Т.И. Курс общей физики (учебное пособие для технических специальностей вузов) / Т.И. Трофимова. – М. : Издательский центр «Академия», 2007, 2008. – 560 с.

Дополнительная литература

1. Савельев, И.В. Курс общей физики. Т. 3 / И.В. Савельев. – М. : Наука, главная редакция физико-математической литературы, 1982. – 304 с.

2. Сивухин, Я.В. Общий курс физики.Т. 3 / Я.В. Сивухин. –М. : Наука, главная редакция физико-математической литературы, 1980. – 520 с.

3. Ландсберг, Г.С. Оптика / Г.С. Ландсберг. – М. : Наука, 1976. – 655 c.