Построение комплексного чертежа модели. Задание для ...ВХ-2-610. Занятие 14 практическая работа 9 Построение комплексного чертежа модели

• Название: Занятие 14 практическая работа 9 Построение комплексного чертежа модели
• Анкор: Построение комплексного чертежа модели
• Дата: 25.12.2021
• Размер: 0.59 Mb.
• Имя файла: Задание для ...ВХ-2-610.docx
• Тип: Занятие; #318197

Занятие №14
ПРАКТИЧЕСКАЯ РАБОТА №9
«Построение комплексного чертежа модели».

Модель – предмет, являющийся совокупностью геометрических тел. Зная способы проецирования геометрических тел, можно построить чертёж модели, состоящей из сочетания нескольких геометрических тел.

В техническом черчении принято называть:

1. 
   фронтальную проекцию – видом спереди;
   
2. 
   горизонтальную проекцию – видом сверху;
   
3. 
   профильную проекцию – видом слева (справа).
   

Изучение учебного материала темы позволит обучающемуся:

1. 
   выполнять комплексные чертежи моделей по их аксонометрии.
   
2. 
   строить третью проекцию модели по двум заданным.
   
3. 
   прочитать учебный материал, составить конспект и подготовиться к закреплению материала и выполнению практического задания.
   

Виды на чертеже располагают в проекционной связи: вид сверху – под видом спереди, а вид слева – справа от него.





Расположение видов на чертеже рис 1.

  Приступая к составлению комплексного чертежа по аксонометрии модели, обучающийся должен мысленно расчленить её на составляющие геометрические тела. Например, на рисунке 63 изображённая модель представляет собой прямоугольный параллелепипед, длина рёбер которого равна 28, 40 и 62мм.



Основание призмы рис 2.

В верхней части имеется сквозной призматический вырез. Основание призмы – трапеция высотой 32мм. Если посмотреть сверху на модель, увидим прямоугольник со сторонами 28 и 40мм.

На виде сверху вырез изобразится двумя сплошными линиями видимого контура и двумя штриховыми линиями невидимого контура. На виде спереди модель представляет прямоугольник со сторонами 40 и 62мм. Наклонные линии и отрезок прямой, равный 26мм, являются проекциями боковых граней призматического выреза.

На виде слева вырез виден не будет, поэтому он показан штриховой линией невидимого контура.

Изображения на видах строится в проекционной связи, чтобы легче было построить виды, не потеряв изображения отдельных элементов модели.

При построении комплексного чертежа модели по её аксонометрическому изображению необходимо выбрать главный вид модели, т.е. вид, дающий наибольшее представление о форме модели. Выполняя комплексный чертёж (рисунок 3), следует сначала вычертить в тонких линиях габаритные очертания трёх проекций, чтобы убедиться, что они размещаются на формате.

Построение начинается с нанесения осей Х, Y, Y1, Z. Затем наносятся оси симметрии и центровые линии. От этих линий в обе стороны откладывают размеры для построения симметричных точек.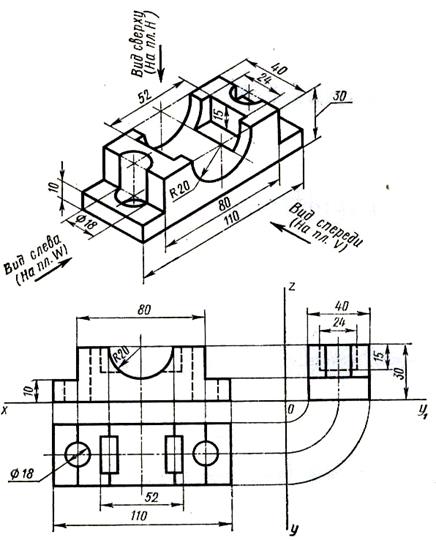



 

Построение комплексного чертежа по аксонометрии модели рис 3.

Закрепление материала:

1 Сформулировать понятие модели.

2 Дать определение:

- вида спереди;

- вида сверху;

- вида слева.

3 Объяснить построение видов детали на чертеже.

 

Проверка степени усвоения материала:

Для подтверждения компетенций по построению комплексного чертежа модели по её аксонометрии обучающиеся выполняют практическое индивидуальное задание в соответствии с вариантом. Задание выполняется на формате А4 в масштабе 1:1.

Название чертежа – «Графическая работа №6а. Комплексный чертёж модели».
Контрольные вопросы:

1. 
   сформулировать понятие чертежа.
   
2. 
   формулировать понятие комплексного чертежа.
   
3. 
   дать понятие плоскости проекций, назвать её виды, обозначение плоскостей проекций.
   
4. 
   определить понятие проекции точки, показать её обозначение в зависимости от плоскости проекций.
   
5. 
   сформулировать понятие аксонометрических проекций.
   
6. 
   назвать виды аксонометрических проекций.
   

Занятие №15
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ ПО РАБОТЕ №10
«АКСОНОМЕТРИЧЕСКАЯ ПРОЕКЦИИ МОДЕЛИ».


Цель: Приобрести навыки построения аксонометрических проекций плоских фигур.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

При составлении технических чертежей иногда возникает необходимость наряду с изображениями предметов в системе ортогональных проекций иметь более наглядные изображения. Для таких изображений применяют метод аксонометрического проецирования (аксонометрия — греческое слово, в дословном переводе оно означает измерение по осям; аксон — ось, метрео — измеряю).
Государственный стандарт устанавливает несколько видов аксонометрических проекций. Для построения наиболее наглядных изображений применяется прямоугольная изометрическая проекция (кратко - изометрия, от греч изо - равный, одинаковый). Положение аксонометрических осей этой проекции приведено на рисунке 1, а. Как видно из чертежа, оси проекции в изометрии располагаются под углом 120° друг к другу. При построении фигур размеры отрезков по осям х0 у0 z0 откладывают без изменения, т. е. действительные.



Рис. 1
В том случае, когда действительные размеры берут только по двум осям (х0, z0), проекцию называют диметрической (от греч. ди - дважды).

Положение осей диметрической проекции дано на рисунке 1, б.
КЛАССИФИКАЦИЯ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ

Все множество аксонометрических проекций подразделяется на две группы:

1 Прямоугольные проекции – получены при направлении проецирования, перпендикулярном аксонометрической плоскости .

2 Косоугольные проекции – получены при направлении проецирования, выбранном под острым углом к аксонометрической плоскости.

Кроме того, каждая из указанных групп делится еще и по признаку соотношения аксонометрических масштабов или показателей (коэффициентов) искажения. Пo-этому признаку аксонометрические проекции можно разделить на следующие виды:

а) Изометрические - показатели искажения по всем трем осям одинаковы (изос — одинаковый).

б) Диметрические - показатели искажения по двум осям равны между собой, а третий не равен (ди — двойной).

в) Триметрические - показатели искажения по всем трем осям не равны между собой. Это аксонометрия (большого практического применения не имеет).



Прямоугольная изометрия рис 2.


Прямоугольная диметрия рис 3.
АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ МНОГОУГОЛЬНИКОВ.

Построение аксонометрических проекций начинают с проведения осей. Параллельно им откладывают размеры отрезков.

Рассмотрим построение аксонометрических проекций плоских геометрических фигур, расположенных в горизонтальной плоскости. Построения даны в изометрической проекции.

Треугольник. Симметрично точке 0⁰ (рис. 4) по оси х⁰ откладывают отрезки С⁰А⁰ и 0⁰Е⁰, равные половине стороны треугольника, а по оси у⁰ - его высоту 0⁰С⁰. Полученные точки А⁰, B⁰ и С⁰ соединяют отрезками прямых.

рис. 4
КВАДРАТ. По оси х⁰ от точки 0⁰ (рис. 6) откладывают отрезок а, равный стороне квадрата, вдоль оси у⁰ - также отрезок а. Затем проводят отрезки, параллельные отложенным.

рис. 5
ШЕСТИУГОЛЬНИК. По оси х⁰ вправо и влево от точки 0⁰ (рис. 70) откладывают отрезки, равные стороне шестиугольника. По оси у⁰ симметрично точке 0⁰откладывают отрезки, равные половине расстояния L между противоположными сторонами шестиугольника, т. е. L/2

рис. 6
 АКСОНОМЕТРИЯ ОКРУЖНОСТИ

В общем случае окружность в асонометрии изображается в виде эллипса.

В прямоугольной аксонометрии большая ось этого эллипса перпендикулярна координатной оси, отсутствующей в плоскости проекций, которой параллельна плоскость окружности (рис. 7 а,б).

На этом рисунке показаны положения осей эллипсов и их размеры в прямоугольной изометрии (рис. 5 а) и в прямоугольной диметрии (рис. 7 б).

 рис. 7


ПРАКТИЧЕСКОЕ ЗАДАНИЕ:

Графическая работа «Аксонометрические проекции плоских фигур».

ЗАДАНИЕ: Выполните прямоугольные и изометрические проекции геометрических фигур: квадрата со стороной 50 мм; правильного треугольника вписанного в окружность Ø50 мм; правильного шестиугольника вписанного в окружность Ø50 мм и круга Ø50 мм.



Рис.1. Прямоугольная и изометрические проекции квадрата

Для выполнения изометрической проекции любой детали необходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.

Правила построения изометрических проекций геометрических фигур. Построение любой плоской фигуры следует начинать с проведения осей изометрических проекций.

При построении изометрической проекции квадрата (рис. 1) из точки О по аксонометрическим осям откладывают в обе стороны половину длины стороны квадрата. Через полученные засечки проводят прямые, параллельные осям.



Рис.2. Прямоугольная и изометрические проекции треугольника

При построении изометрической проекции шестиугольника (рис. 3) из точки О по одной из осей откладывают (в обе стороны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Соединяют полученные засечки отрезками прямых.



Рис.3 Прямоугольная и изометрические проекции шестиугольника

При построении изометрической проекции круга (рис. 4) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, параллельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заменяющий аксонометрическую проекцию круга.



Рис.4. Прямоугольная и изометрические проекции круга