Лекция №1. Занятие №2. Занятие 2 ( Лисичкин В. Т., Соловейчик И. Л. Математика) Раздел Линейная алгебра Тема Матрицы, определители Умножение матриц, возведение в степень. Умножение матриц
 Скачать 284 Kb. Скачать 284 Kb.
|
Занятие №2 (Лисичкин В.Т., Соловейчик И.Л. Математика)Раздел 1. Линейная алгебраТема 1.1. Матрицы, определители Умножение матриц, возведение в степень. 3. Умножение матриц : Д  алеко не все матрицы можно перемножать. алеко не все матрицы можно перемножать. Матрицы A и B (порядок следования важен!) называются согласованными, если число столбцов матрицы A равно числу строк матрицы B. Таким образом, если порядок матрицы A равен m × p , то порядок согласованной с ней матрицы B должен быть равен p × n. Перемножать можно только согласованные матрицы (отметим, что квадратные матрицы одного порядка всегда согласованы). Произведением двух согласованных матриц A (размера m × p) и B (размера p × n ) называется матрица C (размера m × n) , элементы которой вычисляются по правилу: элемент Например, если требуется получить элемент c21, то нужно вторую строку матрицы A "умножить" на первый столбец матрицы B. Рассмотрим конкретные матрицы 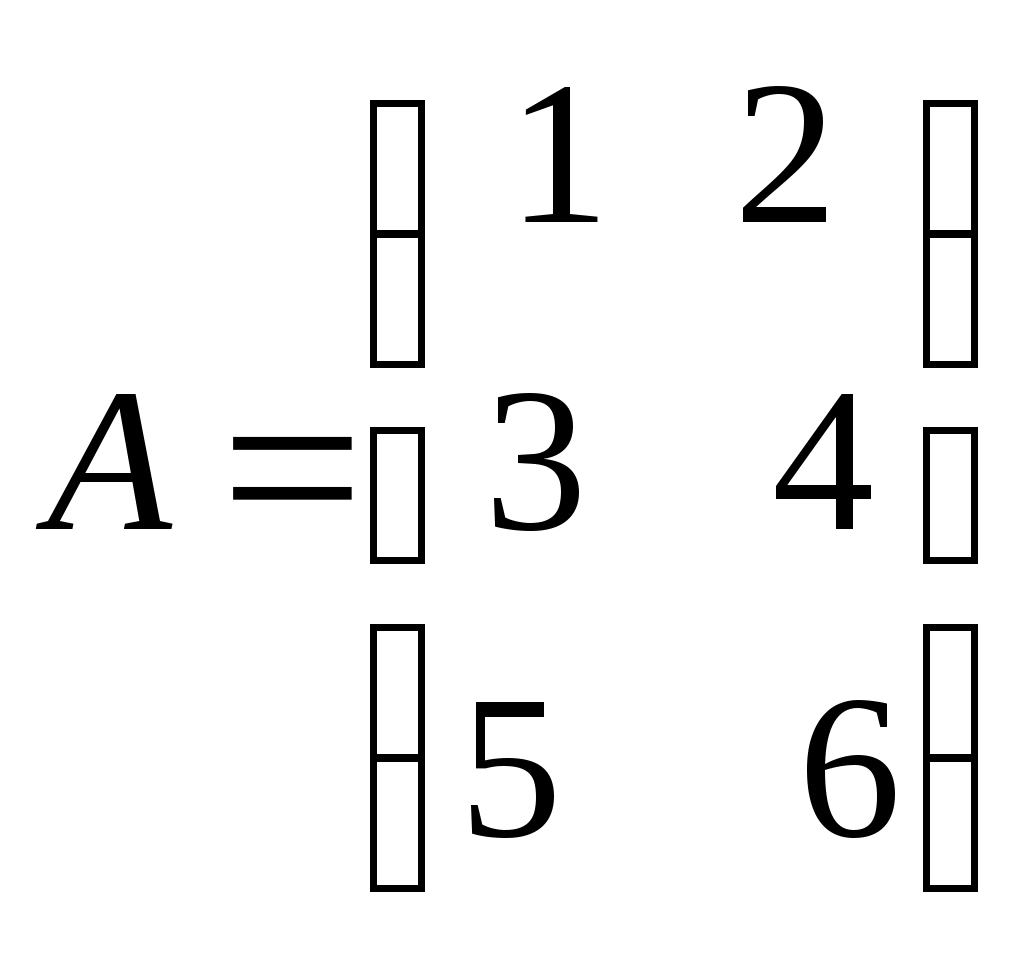 , , Число столбцов матрицы A и число строк матрицы B равны 2, значит, A и B согласованы, причем матрица А∙В будет размера 3х2 . Тогда по определению произведение этих матриц А∙В вычисляется следующим образом:  . .Найти в этом случае произведение B∙A невозможно, т.к. матрицы B и A не согласованы. Отсюда следует, что если две матрицы можно перемножить в одном порядке, то это не означает, что их можно перемножать в другом порядке. Можно показать, что в общем случае, даже когда произведения AB и BA определены, они не всегда дают одну и ту же матрицу (даже размерности матриц АВ и ВА могут быть разными). Свойства операции умножения матриц. А(В+С)=АВ+АС; (А+В)С=АС+ВС; k(АВ)=(kА)В = А(kВ), k - некоторое число; А(ВС)=(АВ)С; А · Е =Е·А =А, где Е – единичная матрица. n×n n×n n×n Пример. Пусть 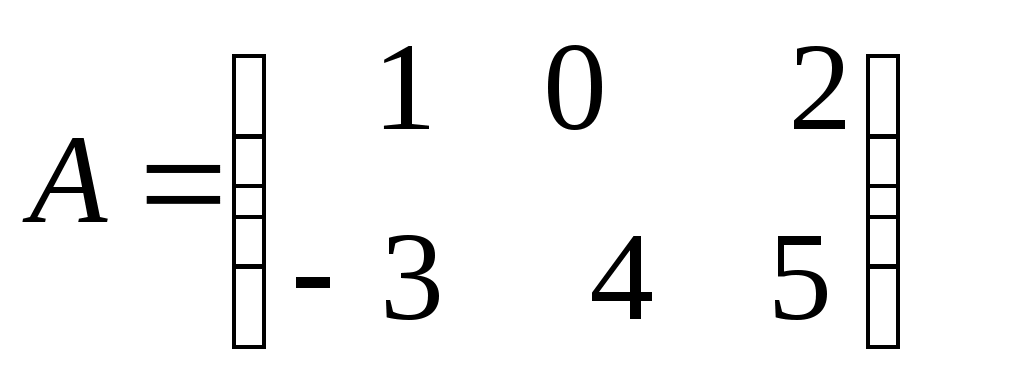 , , 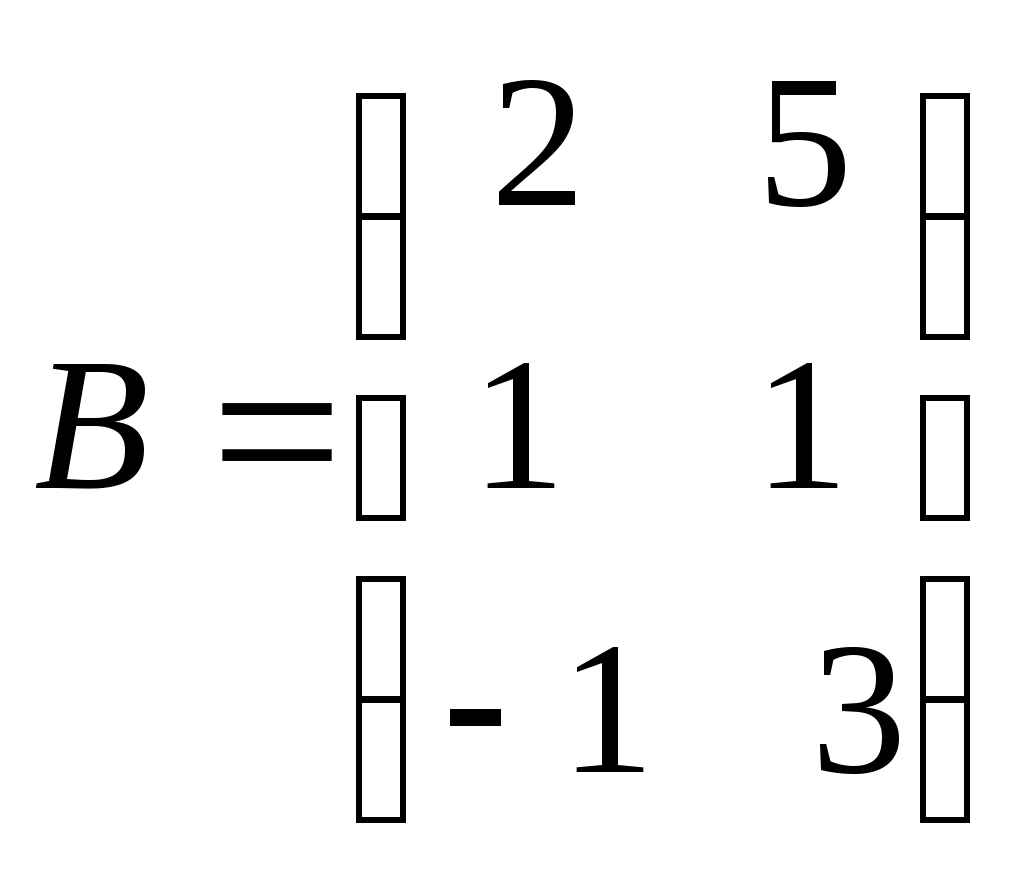 . Тогда . Тогда  , а , а  (проверьте!). Таким образом (проверьте!). Таким образом Это не значит, что вообще не существует двух таких матриц А и В, для которых АВ=ВА. Если для пары матриц А и В это свойство все же выполняется, то такие матрицы называются перестановочными (или коммутативными). Например, коммутативными будут матрицы А = 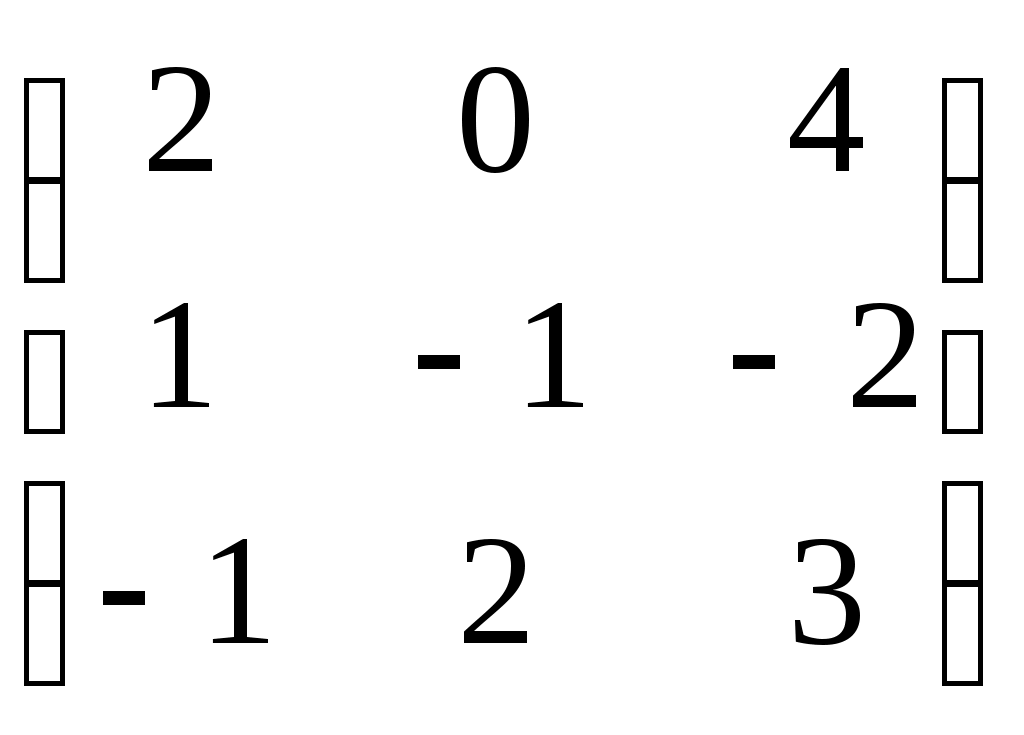 и В = и В = 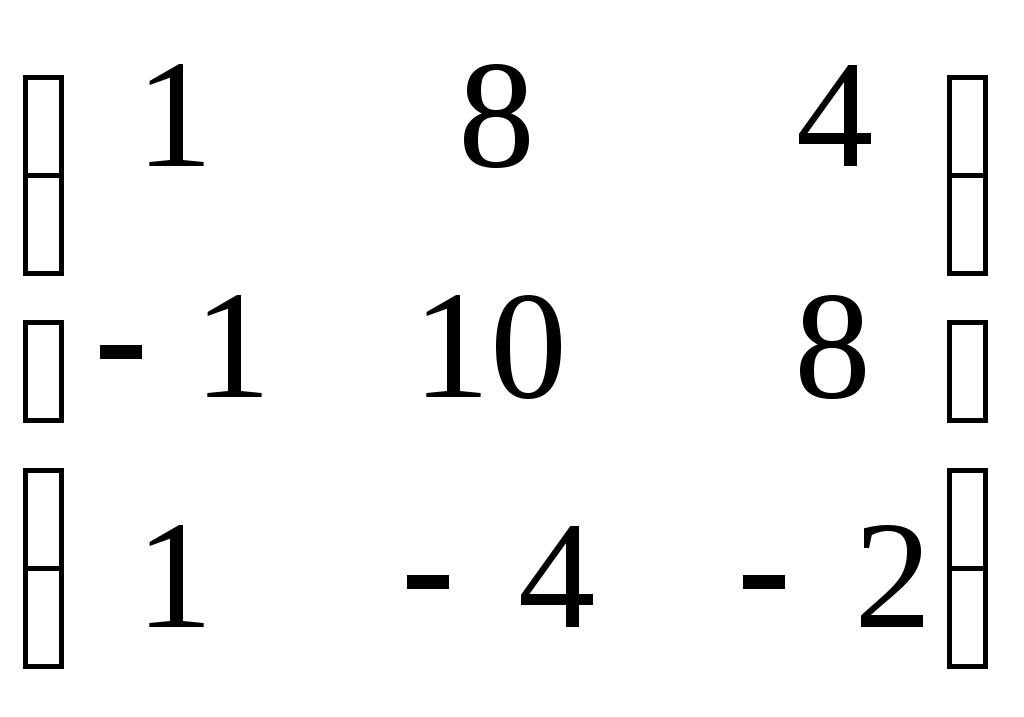 . . Легко перемножением в том и обратном порядке убедиться, что АВ = ВА = 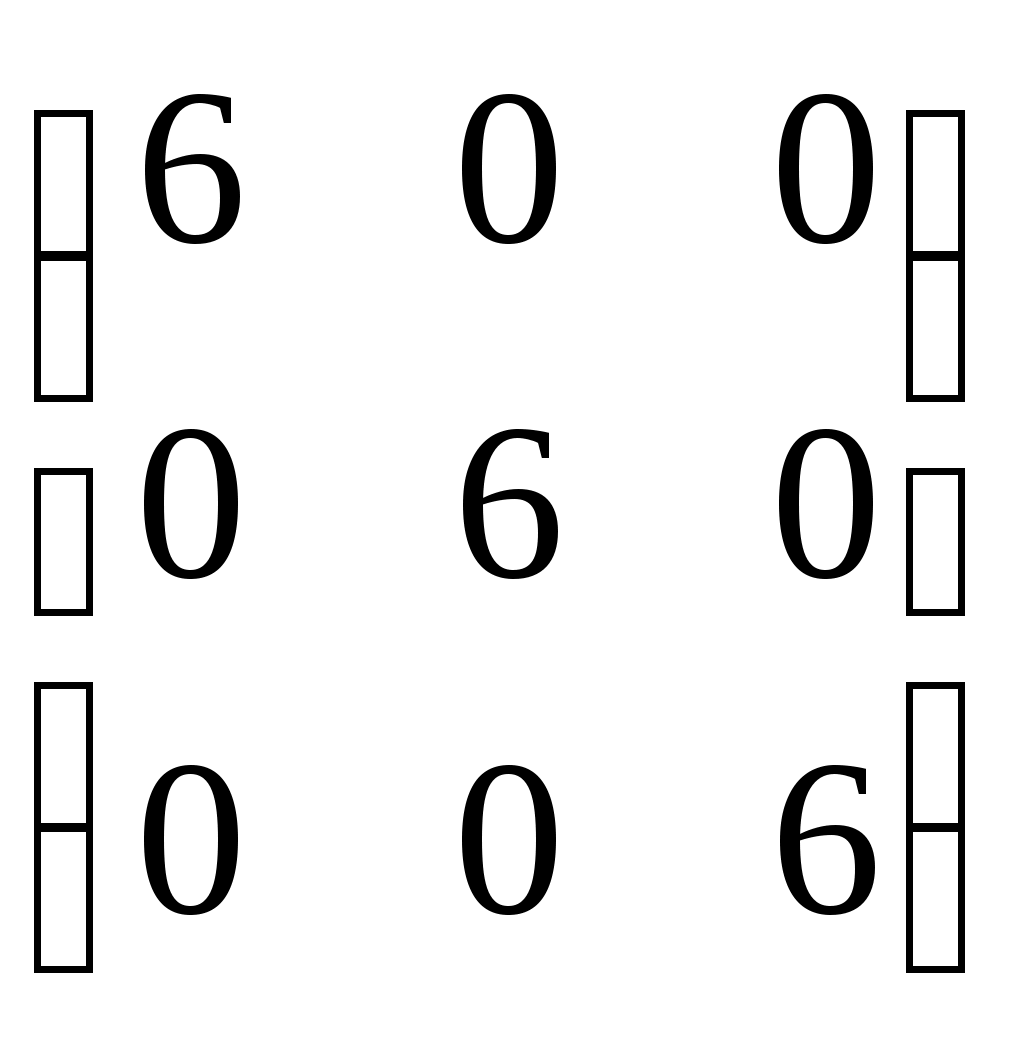 . Отметим, что квадратные матрицы можно перемножать только если они одного порядка. . Отметим, что квадратные матрицы можно перемножать только если они одного порядка. Можно указать одну особенную матрицу, которая перестановочна с любой квадратной матрицей. Это введенная выше единичная матрица. Легко в общем виде показать, что для любой квадратной матрицы А имеет место: А·Е = Е·А = А . Пример 1. Умножение матрицДано: Матрица  ; ;Матрица 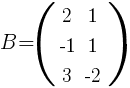 . .Найти: Произведение матриц: A × B = C C — ? Решение: Каждый элемент матрицы С = A × B, расположенный в i-й строке и j-м столбце, равен сумме произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B. Получаем: 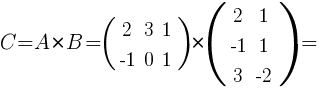 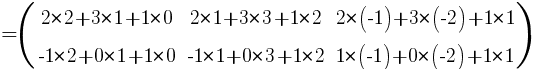 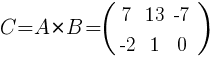 Ответ:  Пример 2. Задание. Вычислить 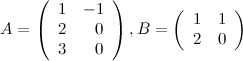 Решение. Так как 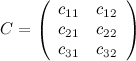 . .Вычислим элементы матрицы Итак,  . .Выполним произведения в более компактном виде: 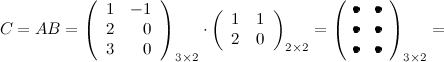 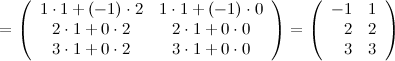 Найдем теперь произведение Ответ. 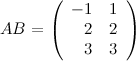 . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы Пример 3. Найти произведения матриц AB и BA, если 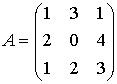 и и 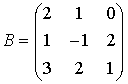 Р е ш е н и е: Имеем 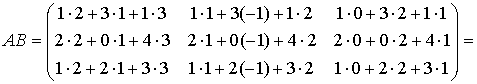  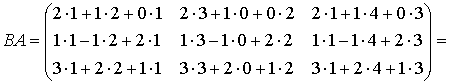  Пример 4. Даны матрицы А =  , В = , В = AT = 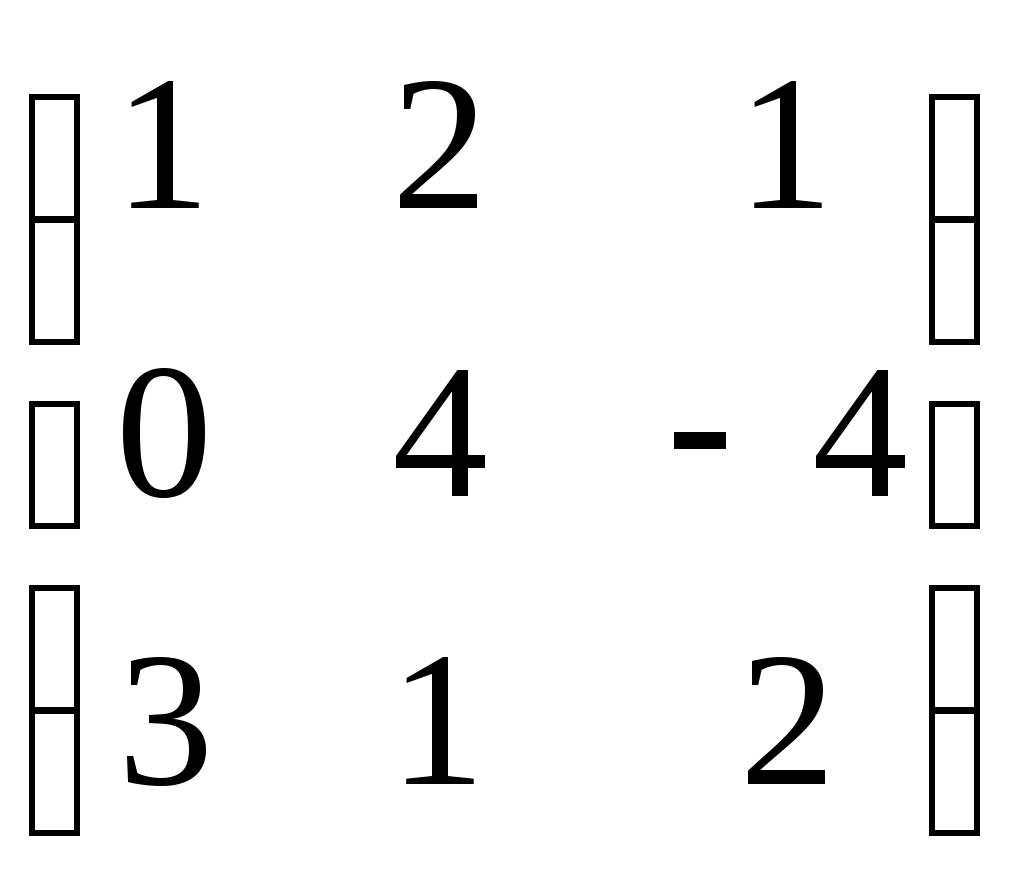 ; ATB = ; ATB = 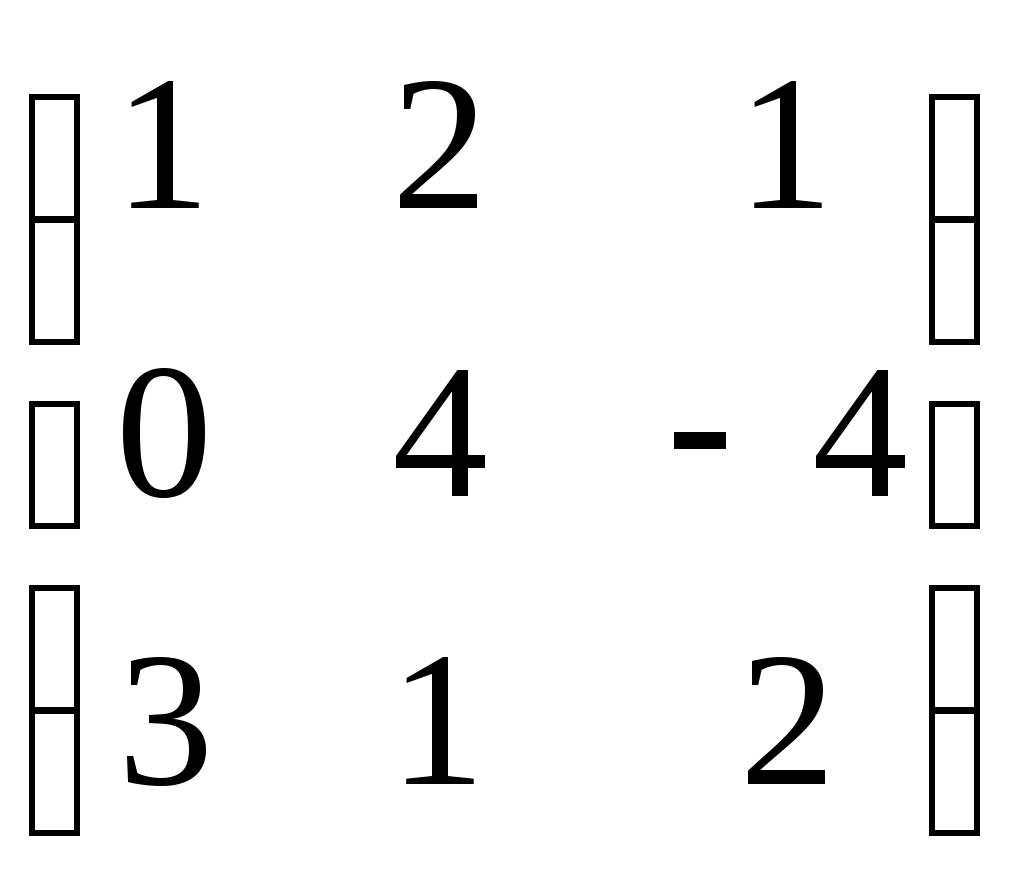 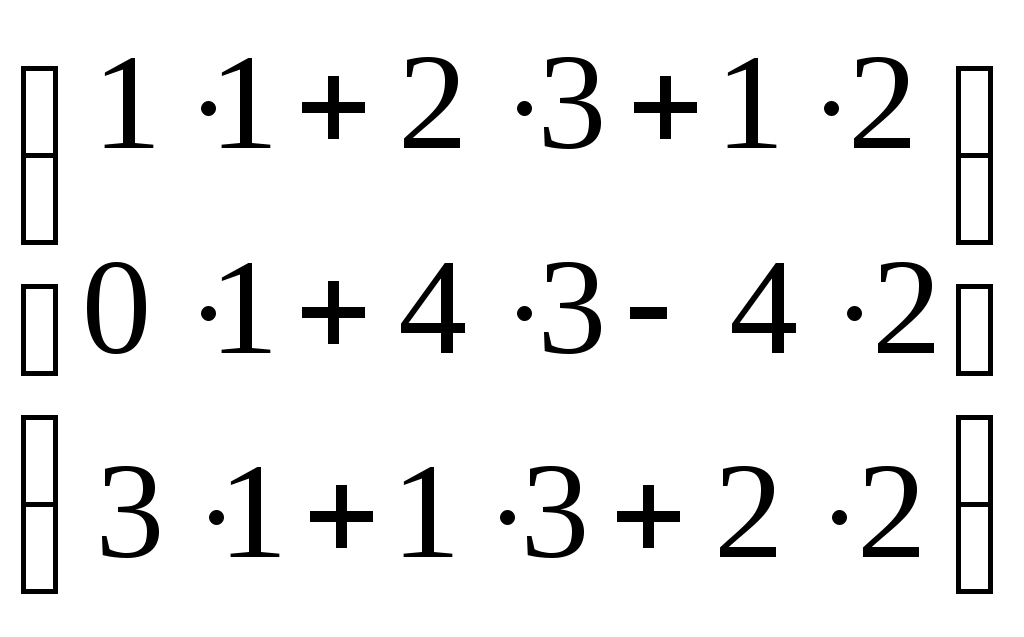 = = C = Пример 5. Найти произведение матриц А = АВ = 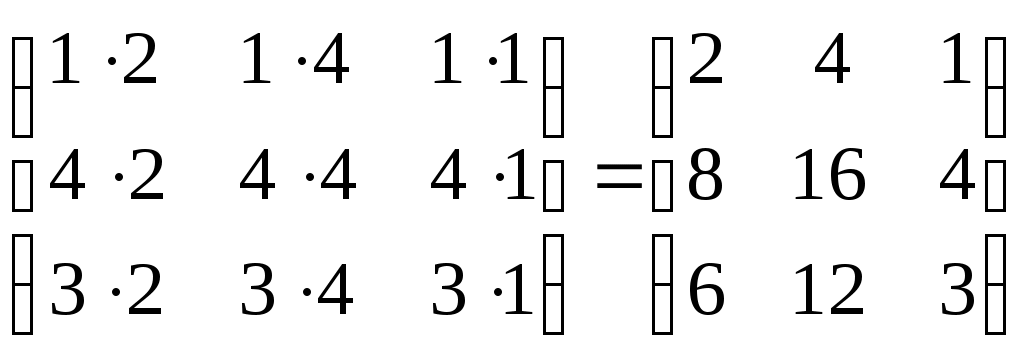 . .ВА = Пример 6. Найти произведение матриц А= АВ = Домашнее заданиеЛ3, стр. 101-102, 105-108 (Пехлецкий И.Д.) Л4, стр. 63-81, №19; 23; 31; 36 (Лисичкин В.Т., Соловейчик И.Л.) №19 Найти произведение АВ 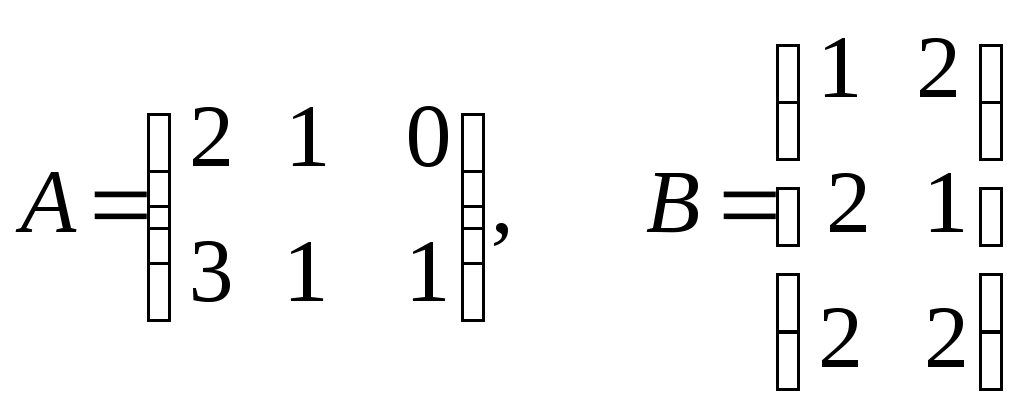 №23 Найти 3А*2В, если 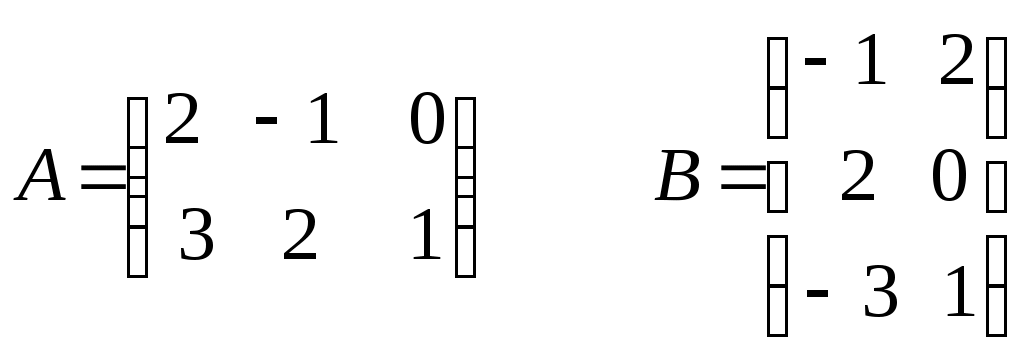 №31 Найти произведение АВ и ВА Матрица A = Матрица B = №36 Даны матрицы А =  , В = , В = Найти АТВ+С. №37 Найти А4 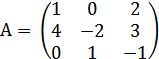 Решение домашнего задания №19 Найти произведение АВ 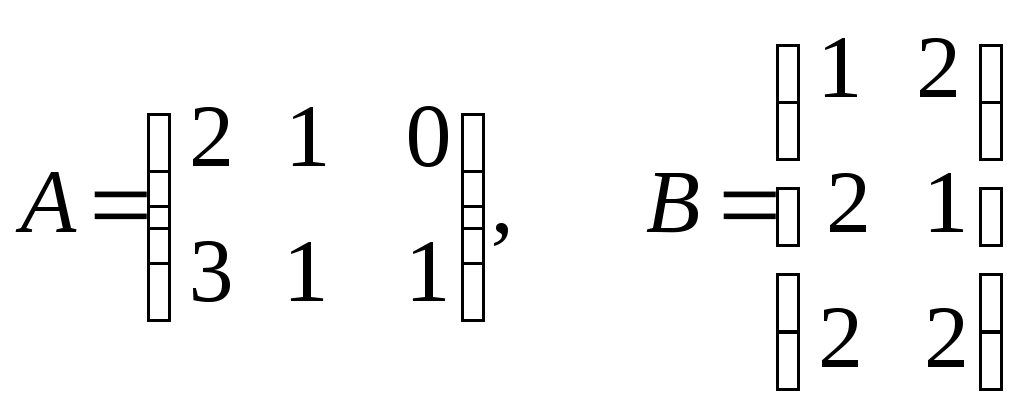 Решение: Есть 2 матрицы: А (2 × 3) и В (3 × 2). Следовательно в результате умножения этих двух матриц получится матрица: С (2 × 2). Рассчитаем по правилу умножения матриц коэффициенты новой матрицы: С (2 × 2). С 11 = (2) × (1) + (1) × (2) + (0) × (2) = 4 С 12 = (2) × (2) + (1) × (1) + (0) × (2) = 5 С 21 = (3) × (1) + (1) × (2) + (1) × (2) = 7 С 22 = (3) × (2) + (1) × (1) + (1) × (2) = 9 Ответ.
№23 Найти 3А*2В, если 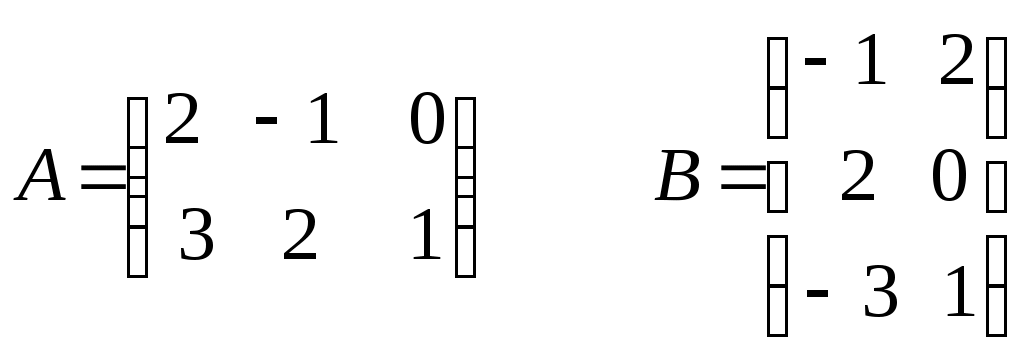 Решение. Есть 2 матрицы: А (2 × 3) и В (3 × 2). Следовательно в результате умножения этих двух матриц получится матрица: С (2 × 2). Рассчитаем по правилу умножения матриц коэффициенты новой матрицы: С (2 × 2). С 11 = (6) × (-2) + (-3) × (4) + (0) × (-6) = -24 С 12 = (6) × (4) + (-3) × (0) + (0) × (2) = 24 С 21 = (9) × (-2) + (6) × (4) + (3) × (-6) = -12 С 22 = (9) × (4) + (6) × (0) + (3) × (2) = 42 Ответ.
№31. В итоге получаем матрицу AxB -- Ответ В итоге получаем матрицу B xA = №36 Даны матрицы А =  , В = , В = Найти АТВ+С. Ответ: AT = 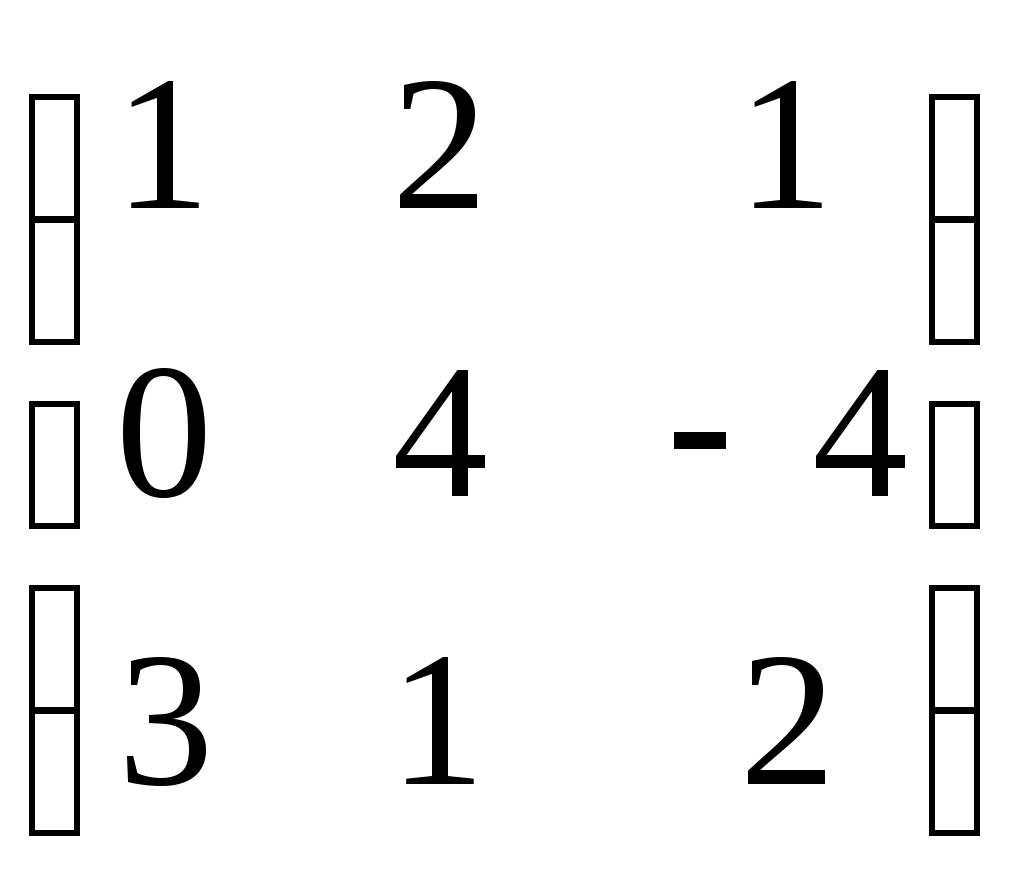 ; ATB = ; ATB = 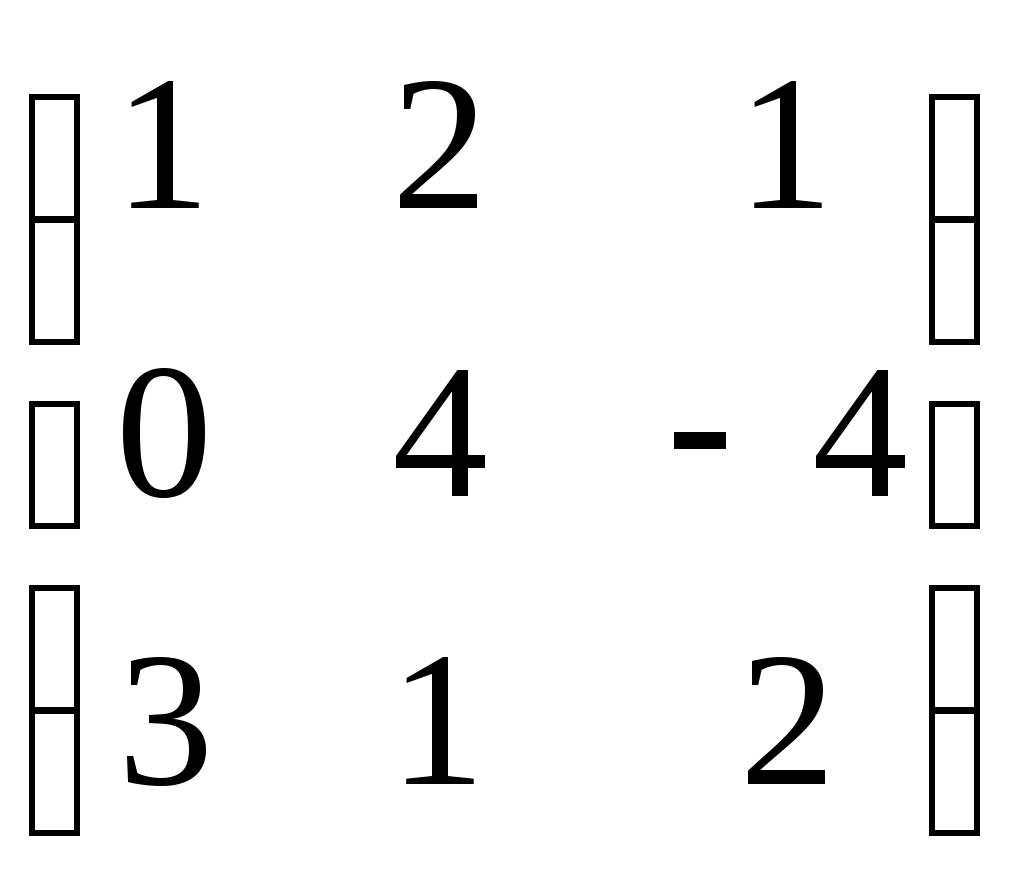 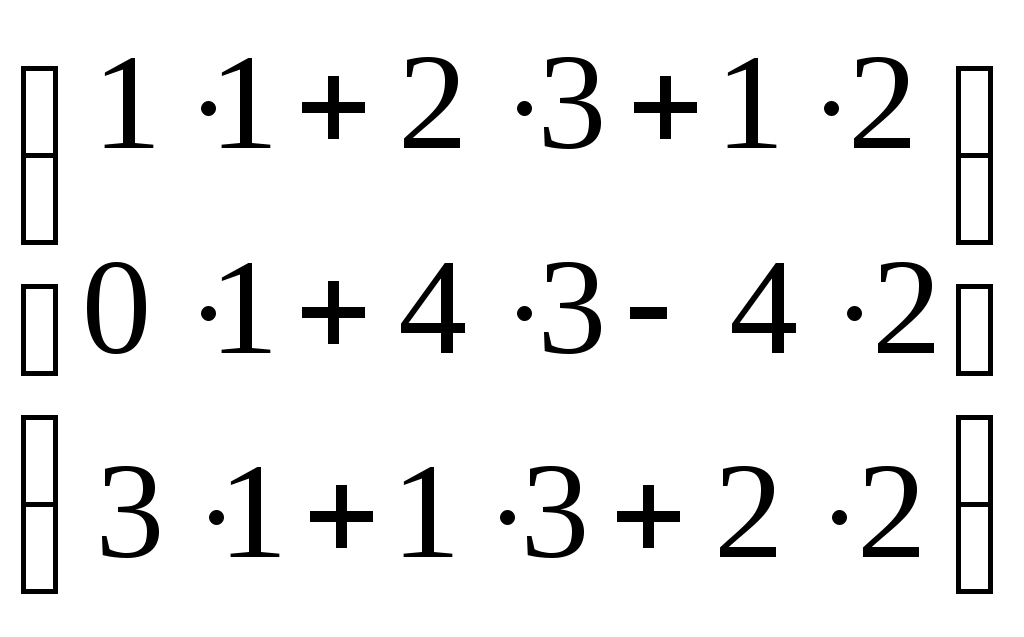 = = C = АТВ+С = №37 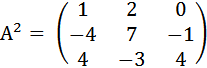 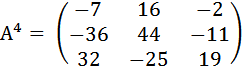 |
