РТС. Обращение матриц Первый способ нахождения обратной матрицы
 Скачать 138.28 Kb. Скачать 138.28 Kb.
|
|
Обращение матриц Первый способ нахождения обратной матрицы. Пусть дана матрица 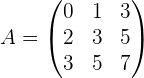 . Обратную матрицу можно вычислить по формуле . Обратную матрицу можно вычислить по формуле Матрица алгебраических дополнений 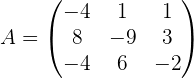 . Транспонируем Матрицу алгебраических дополнений, . Транспонируем Матрицу алгебраических дополнений, 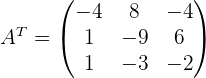 . Теперь найдем обратную матрицу . Теперь найдем обратную матрицу 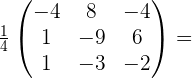 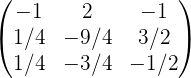 . Если обратная матрица найдена правильно, то при умножение обратной матрицы на исходную получим матрицу, у которой на главной диагонали единицы, а все остальные элементы равны нулю. . Если обратная матрица найдена правильно, то при умножение обратной матрицы на исходную получим матрицу, у которой на главной диагонали единицы, а все остальные элементы равны нулю. 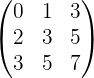 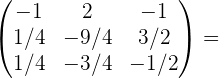 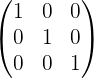 . Так как получили единичную матрицу, то обратная матрица найдена верно. . Так как получили единичную матрицу, то обратная матрица найдена верно.Второй способ нахождения обратной матрицы. Запишем рядом с исходной матрицей единичную 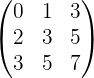 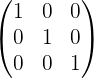 . Любую матрицу можно привести к единичной, это мы и сделаем с нашей матрицей . Любую матрицу можно привести к единичной, это мы и сделаем с нашей матрицей 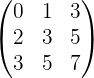 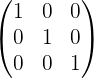 Умножим вторую строку на 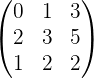 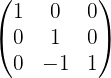 Поменяем первую и третью строки местами. 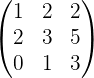 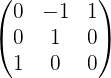 Первую строку умножим на 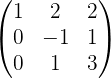 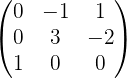 Вторую строку прибавим к третьей. 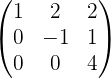 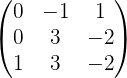 Поделим третью строку на четыре. 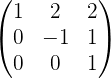 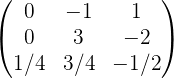 Умножим вторую строку на 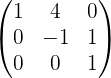 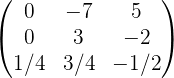 Умножим третью строку на 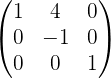 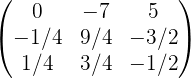 Умножим вторую строку на 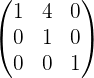 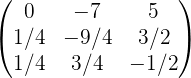 Вторую строку умножим на 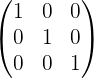 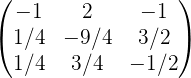 Полученная матрица является обратной. Пусть имеется система линейных уравнений Если уравнение (33) умножить слева и справа на обратную матрицу C–1 то, учитывая, что где E – единичная матрица, получим формулу для решения системы методом обращения матриц: Сложность этого метода заключается в нахождении обратной матрицы С-1, которая рассчитывается следующим образом. Находится транспонированная матрица СТ. Если 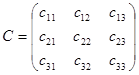 , то , то 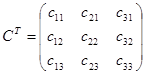 . .Затем рассчитывается матрица алгебраических дополнений: 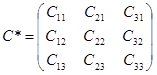 , ,где Сi,j – алгебраические дополнения элементов Сi,j ( Элементы обратной матрицы ищутся из элементов матрицы алгебраических дополнений по формуле: 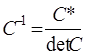 , ,где det C – определитель матрицы С. В Mathcad существует встроенная функция для расчета обратной матрицы. Она вызывается нажатием кнопки Inverse (Инверсия) на панели Matrix (Матрицы) (рис. 41).   Рис. 41. Вызов вычисления обратной матрицы Так каксогласно (34) имеем 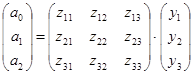 , ,где zij – элементы обратной матрицы С-1. Проведя умножение матрицы на столбец, получим выражения для каждого коэффициента: Пример решения системы линейных алгебраических уравнений методом обращения матриц. Имеем систему (32): 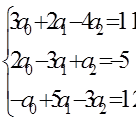 1. Зададим системную переменную, исходные значения матрицы системы и вектора свободных членов 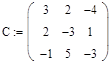 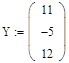 2. Транспонируем матрицу: 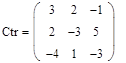 3. Найдем матрицу алгебраических дополнений: 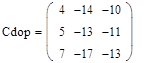 4. Найдем обратную матрицу и осуществим проверку с помощью встроенной функции Mathcad: 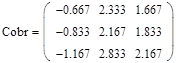 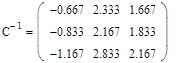 5. Найдем решение системы: 6. Осуществим проверку решения: 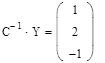 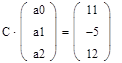 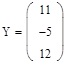 Результаты совпали, следовательно, решение верно. |
