Cистемы линейных однородных уравнений. Теорема Лопиталя.. Системы линейных однородных уравнений. Фундаментальная система решений Система линейных уравнений называется однородной
 Скачать 366.79 Kb.
|
|
Системы линейных однородных уравнений. Фундаментальная система решений Система линейных уравнений называется однородной, если все свободные члены равны нулю: 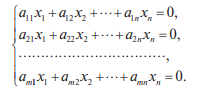 Однородная система всегда совместна, то есть  Она имеет нулевое (тривиальное) решение:  Теорема 1. Для того чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n неизвестных, то есть r < n. Пусть дана однородная система n линейных уравнений с n неизвестными: 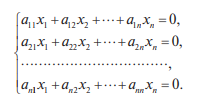 Теорема 2. Для того чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определитель был равен нулю, то есть 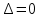 .Пример. Решить систему 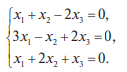 Решение. Вычислим определитель системы: 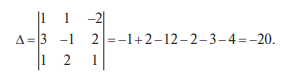 Так как 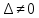 , то система имеет, согласно теореме 2, только одно (нулевое) решение: Запишем решение системы (2.4) 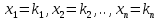 в виде строки  Решения системы линейных однородных уравнений обладают следующими свойствами.  Теорема. Если ранг r основной матрицы системы линейных однородных уравнений меньше числа переменных n, то всякая фундаментальная система решений системы состоит из n–r решений. Общее решение системы линейных однородных уравнений может быть представлено в виде  Где  — любая фундаментальная система решений, — произвольные постоянные и k =n-r.Решения , можно получить, придавая свободным неизвестным поочередно значение 1, полагая остальные свободные неизвестные равными 0.Пример. Найти фундаментальную систему решений и общее решение однородной системы уравнений 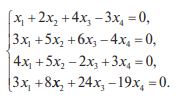 Решение. Найдем ранг системы r:  Оставим первые два уравнения системы: 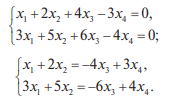 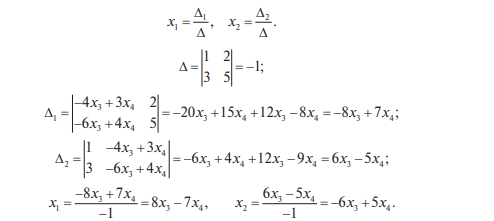 Общее решение системы будет иметь вид 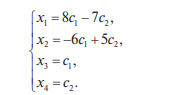 Из общего решения находим фундаментальную систему решений: 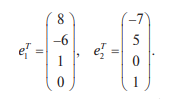 С помощью фундаментальной системы общее решение может быть записано в виде  Теорема о структуре общего решения неоднородной системы линейных уравнений. Общее решение совместной неоднородной системы линейных уравнений равно сумме какого-либо ее частного решения и общего решения однородной системы, соответствующей данной неоднородной. Частное решение неоднородной системы можно получить, приравняв к нулю все свободные неизвестные. Такое решение называется базисным решением (в выбранном базисе) Пример. Найти общее решение системы линейных уравнений   2. Рассмотрим однородную систему, соответствующую данной неоднородной. Поскольку ранг системы равен 2, сразу возьмем эквивалентную систему, содержащую два линейно независимых уравнения:  Перенесем свободные неизвестные в правую часть:  Фундаментальная система решений однородной системы линейных уравнений найдена. Общее решение однородной системы, соответствующей данной неоднородной системе, имеет следующий вид:  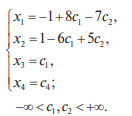 Домашнее задание: Перепишите лекцию и решите задачу. Напишите свое ФИО в тетради 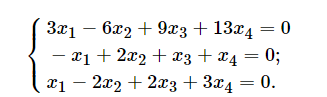 |