Билеты алгем. 9. Теорема КронекераКапелли. Фундаментальная система решений однородной системы линейных уравнений. Теорема о размерности пространства решений. Теорема КронекераКапелли (критерий совместности слу)
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
|
9. Теорема Кронекера-Капелли. Фундаментальная система решений однородной системы линейных уравнений. Теорема о размерности пространства решений. Теорема Кронекера-Капелли (критерий совместности СЛУ): Система линейных уравнений совместна тогда и только тогда, когда ранг ее основной матрицы равен рангу ее расширенной матрицы СЛУ совместна r(A) = r(A | 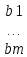 ) )Доказательство: => ∃ 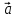 : ( : ( ), что A* ), что A*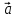 = = 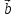 α1 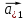 + α2 + α2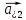 + … + αn + … + αn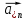 = = 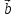 , , 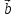 ∈ < ∈ <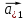 , … , , … ,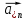 > >< 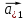 , … , , … ,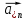 , , 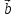 > = < > = <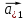 , … , , … ,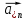 >; >;dim< 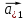 , … , , … ,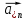 , , 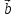 > = dim< > = dim<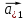 , … , , … ,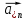 >; >;|| || rc ( A | 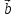 ) = rc(A) ) = rc(A)<= rc (A) = rc ( A | 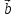 ) => dim< ) => dim<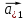 , … , , … ,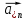 , , 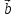 > = dim< > = dim<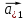 , … , , … ,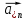 > >< 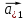 , … , , … ,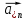 > ⊆ < > ⊆ <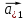 , … , , … ,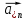 , , 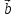 > >↓ < 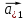 , … , , … ,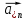 > = < > = <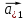 , … , , … ,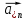 , , 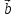 >, тогда >, тогда 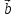 ∈ < ∈ <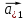 , … , , … ,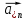 > >Пусть дана однородная система линейных уравнений 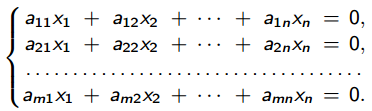 (1) (1)Множество всех решений этой системы образует подпространство пространства R0, называемое пространством решений системы Фундаментальная система решений (ФСР) однородной системы линейных уравнений (ОСЛУ) – базис пространства R0 Теорема о размерности пространства решений. Размерность пространства решений системы равна n – r(A), где n — число неизвестных в системе, а r(A) — ранг основной матрицы системы. dimR0 = n – r(A) Доказательство: r = r(A) Выберем наибольший ненулевой минор (r*r) Б.О.О. это M{1,..,r}{1,..,r} 2) первые r строк матрицы A – базис пространства строк А т.е. ур-ие с r+1 до m – следствия ур-ий с 1 по r. Итак ОСЛУ (1) эквивалентны. 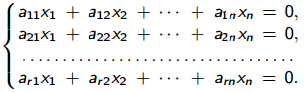 (2) (2)3) перенесем все переменные кроме x1…xr в первую часть и придадим им любые значения из F. 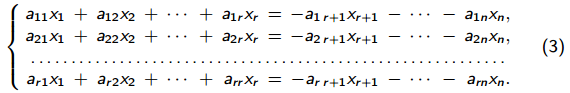 По т.Крамера (3) имеет ровно 1 решение α1 α2 … αr | αr+1 αr+1 … αn 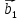 = ( = ( α11 α21 … αr1 | 1 0 … 0 ) α11 α21 … αr1 | 1 0 … 0 )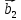 = ( = ( α12 α22 … αr2 | 0 1 … 0 ) α12 α22 … αr2 | 0 1 … 0 )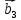 = ( = ( α13 α23 … αr3 | 0 0 … 0 ) α13 α23 … αr3 | 0 0 … 0 ). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 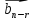 = ( = ( α1n-2 α2n-2 … αrn-2 | 0 0 … 1 ) α1n-2 α2n-2 … αrn-2 | 0 0 … 1 )4) убедимся, что (( 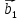 )T…( )T…( 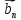 )T) – Базис R0. )T) – Базис R0.β1 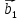 + … + βn-2 + … + βn-2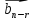 = = 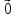 cм. на компоненту r + I; βi * 1 = 0 => βi = 0 т.е. ( 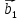 … … 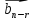 ) – ЛНЗ ) – ЛНЗУбедимся, что <( 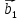 )T…( )T…( 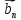 )T> = R0 )T> = R0⊇ ( 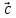 )T ∈ R0 )T ∈ R0( 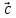 )T = (c1, c2, … , cr, cr+1, cr+2, … , cn) )T = (c1, c2, … , cr, cr+1, cr+2, … , cn)( 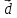 )T = ( )T = ( 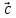 )T - cr+1( )T - cr+1( 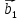 )T - cr+2( )T - cr+2( 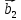 )T - … - cn( )T - … - cn( 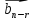 )T ∈ R0 )T ∈ R0( 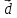 )T = (d1, d2, … , dr, 0, 0, … , 0) по построению )T = (d1, d2, … , dr, 0, 0, … , 0) по построениюПо т.Крамера для (3) при αr+1 = αr+2 = … = αn = 0 d1 = d2 = … = dr = 0 Итак 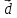 = = 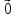 => = ( => = ( 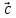 )T = cr+1( )T = cr+1( 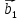 )T + cr+2( )T + cr+2( 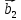 )T + … + cn( )T + … + cn( 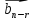 )T ∈ <( )T ∈ <( 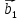 )T…( )T…( 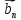 )T> )T>10. Линейное отображение и линейный оператор. Теорема существования и единственности линейного отображения. Матрица линейного отображения в базисах и оператора в базисе. Изменение матрицы отображения при замене базисов. Линейное отображение (ЛОт) Ꭿ: U -> V ∀  , , 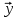 ∈ U Ꭿ( ∈ U Ꭿ( + + 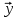 ) = Ꭿ( ) = Ꭿ( )+ Ꭿ( )+ Ꭿ(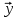 ) )∀α ∈ F; 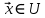 Ꭿ(α Ꭿ(α ) = α*Ꭿ( ) = α*Ꭿ( ) ) 1’) ∀α, β ∈ F;  , , 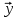 ∈ U ∈ U 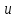 Ꭿ(α Ꭿ(α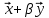 ) = α*Ꭿ( ) = α*Ꭿ( ) + β*Ꭿ( ) + β*Ꭿ(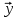 ) )V = U => линейное отображение Ꭿ = линейный оператор d Теорема существования и единственности линейного отображения U, V ЛП над F b = ( 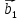 , … , , … ,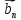 ) – базис U ) – базис Uc = ( 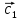 , … , , … ,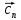 ) – упорядоченная система векторов внутри V (из V), тогда ) – упорядоченная система векторов внутри V (из V), тогда ∃! ЛОт Ꭿ: U -> V, что ∀i ∈ {1..n} Ꭿ( 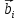 ) = ) = 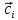 Доказательство: ∃ 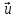 ∈ U => ∃! u1,u2… un ∈ F ∈ U => ∃! u1,u2… un ∈ F 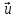 = u1 = u1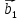 + … + un + … + un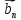 Ꭿ( 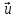 ) = u1 ) = u1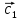 + … + un + … + un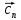 ( ∀i : Ꭿ( ( ∀i : Ꭿ(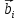 ) = ) = 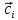 ) )1) 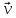 ∈ U ∈ U 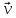 = v1 = v1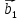 + … + vn + … + vn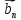 Ꭿ( 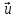 + + 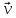 ) = (u1 + v1) ) = (u1 + v1)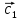 + … + (un + vn) + … + (un + vn)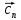 = Ꭿ( = Ꭿ(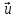 )+ Ꭿ( )+ Ꭿ(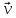 ) )Ꭿ(α 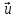 ) = αu1 ) = αu1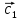 + … + αun + … + αun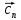 = α*Ꭿ( = α*Ꭿ(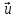 ) ) ! Ᏸ: U->V ( ∀i : Ᏸ ( 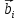 ) = ) = 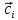 ) )∀ 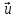 ∈ U Ꭿ( ∈ U Ꭿ(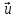 ) = u1 ) = u1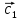 + … + un + … + un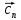 = u1Ᏸ ( = u1Ᏸ (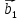 ) + … + unᏰ ( ) + … + unᏰ (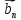 ) = Ᏸ( u1 ) = Ᏸ( u1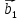 + … + un + … + un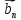 ) =Ᏸ( ) =Ᏸ(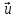 ) => Ꭿ = Ᏸ ) => Ꭿ = Ᏸ b = ( 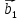 , … , , … ,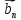 ) – базис U ) – базис Uc = ( 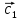 , … , , … ,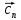 ) – базис V ) – базис VРассмотрим [Ꭿ]cb = ([Ꭿ( 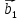 )]c, … , [Ꭿ( )]c, … , [Ꭿ(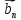 )]c ) )]c )[Ꭿ]cb – матрица линейного оператора от Ꭿ в базисах b и c. U = V, c = b : [Ꭿ]bb = [Ꭿ]b – матрица ЛО Ꭿ в базисе b. Изменение матрицы отображения при замене базисов.  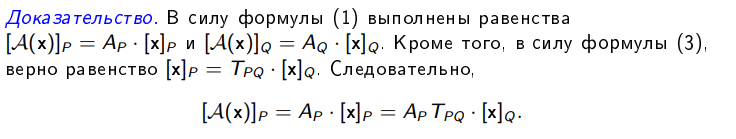  11. Сумма линейных операторов, произведение линейного оператора на скаляр. Изоморфизм векторных пространств линейных операторов и матриц. Характеристический многочлен линейного оператора. Теорема Гамильтона-Кэли для линейных операторов.  ∀  ∈ U (Ꭿ+Ᏸ)( ∈ U (Ꭿ+Ᏸ)( ) = Ꭿ( ) = Ꭿ( )+ Ᏸ( )+ Ᏸ( ) ) ∀  ∈ U, α ∈ F (αᎯ)( ∈ U, α ∈ F (αᎯ)( ) = α*Ꭿ( ) = α*Ꭿ( ) )Изоморфизм векторных пространств линейных операторов и матриц    12. Образ и ядро линейного оператора. Теорема о размерности образа и ядра. Алгоритмнахождения базисов образа и ядра. Пусть Ꭿ - линейный оператор в векторном пространстве V (Ꭿ: V -> V) Образом Ꭿ называется множество всех векторов, 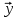 ∈ V таких, что Ꭿ( ∈ V таких, что Ꭿ( ) = ) = 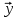 для некоторого для некоторого  ∈ V ∈ VImᎯ = { 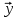 ∈ V | ∃ ∈ V | ∃ ∈ V Ꭿ( ∈ V Ꭿ( ) = ) = 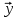 } }Ядром Ꭿ называется множество всех векторов  ∈ V таких, что Ꭿ( ∈ V таких, что Ꭿ( ) = 0 ) = 0KerᎯ = {  ∈ V | Ꭿ( ∈ V | Ꭿ( ) = 0} ) = 0}Размерность образа линейного оператора Ꭿ называется рангом Ꭿ r(Ꭿ) = dimImᎯ Размерность ядра оператора Ꭿ называется дефектом d(Ꭿ) = dimKerᎯ Теорема о размерности образа и ядра: r(Ꭿ) + d(Ꭿ) = dimV   Алгоритм нахождения базисов образа и ядра. Алгоритм Чуркина  13. Собственные векторы и собственные значения линейного оператора. Теоремы о собственных векторах, относящихся к одному и тому же собственному значению и к разным собственным значениям. Собственные значения и корни характеристического уравнения оператора. Линейные операторы, приводимые к диагональному виду   ∈ V собственный вектор ЛОп Ꭿ с собственным значением α, если ∈ V собственный вектор ЛОп Ꭿ с собственным значением α, если1)  ≠ ≠ 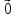 2) Ꭿ(  ) = α* ) = α* Теоремы о собственных векторах, относящихся к одному и тому же собственному значению  Sα= {  \ Ꭿ( \ Ꭿ( ) = α* ) = α* }, тогда Sα ≤ V }, тогда Sα ≤ VДоказательство: a, b ∈ F,  , , 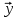 ∈ Sα ∈ Sα Ꭿ(a  +b +b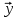 ) = aᎯ( ) = aᎯ( ) + bᎯ( ) + bᎯ(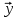 ) = aα ) = aα + bα + bα = α(a = α(a +b +b ) )Теоремы о собственных векторах к разным собственным значениям.    Собственные значения и корни характеристического уравнения оператора   Линейные операторы, приводимые к диагональному виду    |
