Тема 2. Зависимые и независимые случайные события. Основные формулы сложения и умножения вероятностей
 Скачать 442.5 Kb.
|
|
ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ СОБЫТИЯ. ОСНОВНЫЕ ФОРМУЛЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ Понятия зависимости и независимости случайных событий. Условная вероятность. Формулы сложения и умножения вероятностей для зависимых и независимых случайных событий. Формула полной вероятности и формулы Бейеса.
Найдем вероятность суммы событий  и  (в предположении их совместности либо несовместности).Теорема 2.1. Вероятность суммы конечного числа несовместных событий равна сумме их вероятностей:  .Пример 1. Пусть вероятность того, что в магазине очередной будет продана пара мужской обуви  -го размера, равна  ,  -го -  ,  -го или большего -  . Найти вероятность того, что очередной будет продана пара мужской обуви не менее -го размера.Решение . Искомое событие  произойдет, если будет продана пара обуви -го размера (событие ), или -го (событие ) или не менее -го (событие  ), т. е. событие есть сумма событий , , . События , и несовместны. Поэтому, применяя теорему сложения вероятностей, получим:  .Пример 2. В условиях примера 1 найти вероятность того, что очередной будет продана пара обуви меньше -го размера.Решение. События “очередной будет продана пара обуви меньше -го размера” и “будет продана пара обуви размера не меньше -го” - противоположные. Поэтому по формуле (1.2) вероятность искомого события равна ,поскольку  , как это было найдено в примере 1.Теорема 2.1 сложения вероятностей справедлива только для несовместных событий. Использование ее для нахождения вероятности совместных событий может привести к неправильным, а иногда и абсурдным выводам, что хорошо видно на следующем примере. Пусть всхожесть семян оценивается вероятностью  . Какова вероятность того, что из трех посеянных семян взойдет какое-либо одно (безразлично какое)? Через , , обозначим события, состоящие в том, что взойдут соответственно первое, второе, третье семена. Если для отыскания искомой вероятности мы применим теорему 2.1 сложения вероятностей, то получим  . Вероятность события оказалась больше единицы. Абсурдность ответа объясняется тем, что события , , являются совместными. Действительно, если произошло, например, событие (взошло первое семя), то это не исключает того, что произойдет и событие (взойдет второе семя).Сформулируем теорему сложения вероятностей в случае двух совместных событий (будет учитываться вероятность их совместного появления). Теорема 2.2. Вероятность суммы двух совместных событий равна сумме вероятностей этих двух событий без вероятности их совместного появления:  .2. Зависимые и независимые события. Условная вероятность. Различают зависимые и независимые события. Два события называется независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не связанные между собой, то остановки этих линий являются независимыми событиями. Пример 3. Монета брошена два раза. Вероятность появления “герба” в первом испытании (событие ) не зависит от появления или непоявления “герба” во втором испытании (событие ). В свою очередь, вероятность появления герба во втором испытании не зависит от результата первого испытания. Таким образом, события и - независимые.Несколько событий называются независимыми в совокупности, если любое из них не зависит от любой комбинации остальных. События называются зависимыми, если одно из них изменяет вероятность появления другого. Например, две производственные установки связаны единым технологическим циклом. Тогда вероятность выхода из строя одной из них зависит от того, в каком состоянии находится другая. Вероятность одного события , вычисленная в предположении осуществления другого события , называется условной вероятностью события и обозначается через  .Условие независимости события от события записывают в виде   , а условие зависимости - в виде  . Рассмотрим пример вычисления условной вероятности события.Пример 4. В ящике находятся  резцов - два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.Решение. Обозначим через извлечение изношенного резца в первом случае, а через  - извлечение нового. Тогда  ,  . Поскольку извлеченный резец в ящик не возвращается, то изменяется соотношение между количествами изношенных и новых резцов. Следовательно, вероятность извлечения изношенного резца во втором случае зависит от того, какое событие осуществилось перед этим. Обозначим через событие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими: ,  .Следовательно, вероятность события зависит от того, произошло или нет событие .3. Формулы умножения вероятностей. Пусть события и независимые, причем вероятности этих событий известны. Найдем вероятность совмещения событий и .Теорема 2.3. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:  .Следствие 2.1. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий.:  .Пример 5. Имеется три ящика, содержащих по  деталей. В первом ящике -  , во втором -  , в третьем -  стандартных деталей. Из каждого ящика наудачу вынимается по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.Решение. Вероятность того, что из первого ящика вынута стандартная деталь (событие ) равна  . Вероятность того, что из второго ящика вынута стандартная деталь (событие ) равна  . Вероятность того, что из третьего ящика вынута стандартная деталь (событие ) равна  . Так как события , и независимые в совокупности, то искомая вероятность (по теореме умножения) равна  .Пусть события и зависимые, причем вероятности  и известны. Найдем вероятности совмещения этих событий, т. е. вероятность того, что появится и событие , и событие .Теорема 2.4. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:  , .Следствие 2.2. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились: Пример 6. В урне находится белых,  черных и  синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в урну. Найти вероятность того, что при первом испытании появится белый шар (событие ), при втором - черный (событие ) и при третьем - синий (событие ).Решение. Вероятность появления белого шара при первом испытании равна  .Вероятность появления черного шара при втором испытании, вычисленная в предположении, что при первом испытании появился белый шар, т. е. условная вероятность равна  .Вероятность появления синего шара при третьем испытании, вычисленная в предположении, что при первом испытании появился белый шар, а при втором - черный, равна  .Искомая вероятность равна   .4. Формула полной вероятности. Теорема 2.5. Если событие может наступить только при условии появления одного из событий  , образующих полную группу несовместных событий, то вероятность события равна сумме произведений вероятностей каждого из событий на соответствующую условную вероятность события : . (2.1)Эта формула носит название формулы полной вероятности. Пример 7. На сборочный конвейер поступают детали с трех станков. Производительность станков неодинакова. Первый дает  % программы, второй -  %, а третий -  %. Если в сборку попадает деталь, сделанная на первом станке, то вероятность получения годного узла равна  . Для продукции второго и третьего станков соответствующие вероятности равны  и  . Определить вероятность того, что узел, сходящий с конвейера, годный.Решение. Обозначим через событие, означающее годность собранного узла; через  ,  и  события, означающие, что детали сделаны соответственно на первом, втором, третьем станках. Тогда имеем: ;  ;   ;  ;  .Искомая вероятность равна:     .5. Формулы Бейеса. Формулы Бейеса применяются при решении практических задач, когда событие , появляющееся совместно с каким-либо из событий , , … ,  , которые образуют полную группу несовместимых событий, произошло и требуется произвести количественную переоценку вероятностей событий , , … , . Априорные (до опыта) вероятности  ,  , … , известны. Требуется вычислить апостериорные (после опыта) вероятности, т. е. по существу нужно найти условные вероятности  ,  , … , . Для события  формула Бейеса выглядит так: .Раскрывая в этом равенстве 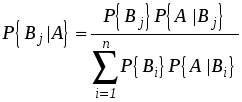по формуле полной вероятности (2.1), имеем: .Пример 8. Пользуясь данными примера 7, рассчитать вероятности того, что в сборку попала деталь, изготовленная на первом, втором и третьем станках соответственно, если узел сходящий с конвейера, годный. Решение. Расчет условных вероятностей произведем по формуле Бейеса. Имеем: для первого станка  ;для второго станка  ;для третьего станка  .ЗАДАЧИ 1. Бросили монету и игральную кость. Определить, зависимы или независимы события: - выпал “герб”; - выпало четное число очков.Ответ: независимы. 2. Брошены последовательно три монеты. Определить, зависимы или независимы события: - выпадение “герба” на первой монете; - выпадение хотя бы одной “решетки”.Ответ: зависимы. 3. Бросили игральную кость. Какова вероятность того, что выпало простое число очков, если известно, что число выпавших очков нечетно ? Ответ: 2/3. 4. В ящике лежат  красных, зеленых и синих шаров. Наудачу вынимается два шара. Какова вероятность, что извлечены шары разного цвета, если известно, что не извлечен синий шар ?Ответ: 48/95. 5. В одном ящике белых и красных шаров, в другом ящике белых и красных шаров. Найти вероятность того, что хотя бы из одного ящика будет извлечен один белый шар, если из каждого ящика извлечено по одному шару.Ответ: 7/9. 6. Вероятность того, что в течение одной смены возникнет неполадка станка, равна  . Какова вероятность того, что не произойдет ни одной неполадки за три смены ?Ответ: (0,95)3=0,857375. 7. В ящике красных и  синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность того, что пуговицы будут одноцветными ?Ответ: 0,5. 8. Найти вероятность того, что наудачу взятое двузначное число окажется кратным  , либо , либо тому и другому одновременно.Ответ: 0,6. 9. Студент пришел на зачет, зная из вопросов только  . Какова вероятность сдать зачет, если после отказа отвечать на вопрос преподаватель задает еще один вопрос ?Ответ: 28/29. 10. Имеется два одинаковых ящика с шарами. В первом ящике белых и  черный шар, во втором - белый и черных шара. Наудачу выбирают один ящик и извлекают из него шар. Какова вероятность, что извлеченный шар окажется белым ?Ответ: 13/30. 11. В цехе работают станков. Из них марки , марки и марки . Вероятность того, что качество деталей окажется отличным, для этих станков соответственно равна:  , и . Какой процент отличных деталей выпускает цех в целом ?Ответ: 83%. 12. Студент знает не все экзаменационные билеты. В каком случае вероятность вытащить неизвестный билет будет для него наименьшей, когда он тащит билет первым или последним ? Ответ: безразлично. 13. На фабрике, изготовляющей болты, первая машина производит  %, вторая -  %, третья -  % всех изделий. В их продукции брак составляет соответственно %, % и %. а) Какова вероятность того, что случайно выбранный болт дефектный ? б) Случайно выбранный из продукции болт оказался дефектным. Какова вероятность того, что он был произведен первой, второй, третьей машиной ? Ответ: а) 0,0345; б) 125/345, 140/345, 80/345. |