Техническая эстетика, золотое сечение Угнту. Реферат. Золотое сечение студент группы мпсЗ1701 Проверил И. Е. Ишемгужин Уфа 2020 содержание введение. 3 Историческая часть. 4 Золотое сечение. 8 Золотые фигуры. 10
 Скачать 432.96 Kb. Скачать 432.96 Kb.
|
|
Министерство науки и высшего образования российской федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Уфимский государственный нефтяной технический университет» Факультет заочного обучения Кафедра «Машины и оборудования нефтегазовых промыслов» РЕФЕРАТ по дисциплине «Основы технической эстетики по теме: ЗОЛОТОЕ СЕЧЕНИЕ Выполнил: студент группы МПсЗ-17-01 Проверил: И.Е. Ишемгужин Уфа 2020 СОДЕРЖАНИЕ Введение. 3 1. Историческая часть. 4 2. Золотое сечение. 8 3. «Золотые» фигуры. 10 3.1. «Золотой» треугольник. 10 3.2. «Золотой» прямоугольник. 11 3.4. «Золотой» пятиугольник и пентаграмма. 12 3.5. Спираль Архимеда. 13 4. Ряд Фибоначчи. 14 5. «Золотые» пропорции в природе. 15 6. «Золотые» пропорции в теле человека. 16 7. «Золотое сечение» в живописи. 17 8. «Золотое сечение» в архитектуре. 18 Заключение. 20 Литература. 21 ВВЕДЕНИЕ Золотое сечение –это деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине. Данная тема привлекла меня тем, что термин «Золотое сечение» встречается во многих сферах человеческой деятельности, а также в окружаемом нас мире. В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника. Интерес и споры вокруг этого понятия не исчезли и по сегодняшний день. Многие люди стремятся найти золотое сечение во всём, есть и те, кто считают, что золотое сечение имеет множество замечательных свойств, но ещё больше свойств вымышленных. Людей с давних времён волновал вопрос, подчиняются ли такие неуловимые вещи как красота и гармония, каким-либо математическим расчётам. Можно ли «проверить алгеброй гармонию?» - как сказал А.С. Пушкин. Конечно, все законы красоты невозможно вместить в несколько формул, но, изучая математику, мы можем открыть некоторые слагаемые прекрасного. Тема «Золотое сечение» актуальна в современном развивающемся мире, так например, в архитектуре, живописи «правило золотого сечения» встречается очень часто. Существуют ли другие сферы деятельности, в которых возможно применение данного математического термина? 1 Историческая часть Понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамсеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.  Рисунок 1.Античный циркуль золотого сечения. Греки же были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников. Платон (427...347 гг. до н.э.) также знал о золотом делении. Его диалог "Тимей" посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления. Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления. 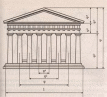 Рисунок 1.Парфенон. В дошедшей до нас античной литературе золотое деление впервые упоминается в "Началах" Евклида. Во 2-й книге "Начал" дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др.. В средневековой Европе с золотым делением познакомились по арабским переводам "Начал" Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным. В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением, как в геометрии, так и в искусстве, особенно в архитектуре. Леонардо да Винчи, художник и ученый, видел, что в итальянских художниках большой эмпирический опыт, но недостаток знаний. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли "Божественная пропорция" с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее "божественную суть" как выражение божественного триединства: бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок - бога отца, а весь отрезок - бога духа святого). Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное. В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет: "Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать". Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица - ртом и т.д. Известен пропорциональный циркуль Дюрера. В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы "вместе с водой выплеснули и ребенка". Вновь "открыто" золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд "Эстетические исследования". С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях "математической эстетикой". 2 Золотое сечение Рассмотрим отрезок AB рисунок 3.  Рисунок 3.Отрезок АВ Его можно разделить точкой Е на две части бесконечным множеством способов, но говорят что точка Е производит золотое сечение отрезка АВ, если выполняется пропорция: длина меньшего отрезка так относится к длине большего, как больший отрезок относится к длине всего отрезка , т.е. 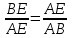 . .Золотое сечение –это деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине. Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки (Рис.4). 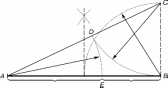 Рисунок 4. Деление отрезка прямой по золотому сечению. Дано: отрезок АВ. Построить: золотое сечение отрезка АВ, т.е. точку Е так, чтобы 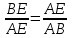 . .Построение. Построим прямоугольный треугольник, у которого один катет в два раза больше другого. Для этого восстановим в точке В перпендикуляр к прямой А и на нем отложим отрезок ВС=0,5АВ . Далее, соединим точки А и С, отложим отрезок CD=CB, и наконец AE=AD. Точка Е является искомой, она производит золотое сечение отрезка АВ. Доказательство. ΔАВС – прямоугольный по построению. По теореме Пифагора АС2=АВ2+ВС2. Так как отрезок АС=AD+DC, то равенство перепишем в виде: (AD+DC)2=АВ2+ВС2 AD=АЕ, DC=СВ=  (АЕ+  )2=АВ2+( )2=АВ2+( )2 )2АЕ2+2  АЕ∙АВ+ АЕ∙АВ+ АВ2= АВ2+ АВ2= АВ2+ АВ2 АВ2АЕ2+АЕ∙АВ = АВ2 АЕ2 = АВ2 - АЕ∙АВ АЕ2 = АВ (АВ – АЕ), так как АВ – АЕ = ВЕ АЕ2 = АВ∙ ВЕ,  Исследование. Задача имеет единственное решение. 3 Золотые» фигуры 3.1. Золотой треугольник Проводим прямую АВ (Рис.5). От точки А откладываем на ней три раза отрезок O произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1 откладываем на линию Ad1, получая точку С. Точка С разделила линию Ad1 в пропорции золотого сечения. 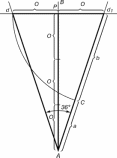 Рисунок 5. Построение «золотого» треугольника. Итак, золотым называется такой равнобедренный треугольник, основание и боковая сторона которого находятся в золотом отношении: 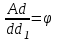  3.2. «Золотой» прямоугольник. Если провести психологический опыт, попросить нескольких человек начертить на альбомном листе произвольный прямоугольник, то у многих отношение сторон оказалось близким к числу φ. И это не случайно, так как кажутся красивыми и гармоничными именно те фигуры, в которых есть элементы, связанные друг с другом золотым отношением. Прямоугольник, стороны которого находятся в золотом отношении, т.е. отношение ширины к длине даёт число φ, называется золотым прямоугольником. Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый (рис. 6). 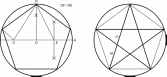 Рисунок 6. Построение правильного пятиугольника и пентаграммы. Для построения пентаграммы необходимо построить правильный пятиугольник. Пусть О - центр окружности, А - точка на окружности и Е - середина отрезка ОА. Перпендикуляр к радиусу ОА, восстановленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE=ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией. Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения. Есть и золотой кубоид- это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618. Звездчатый пятиугольник называется пентаграммой (Рис.6). Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком. Бытует легенда о том, что один из пифагорейцев больным попал в дом к незнакомым людям. Они старались его выходить, но болезнь не отступала. Не имея средств заплатить за лечение и уход, больной перед смертью попросил хозяина дома нарисовать у входа пятиконечную звезду, объяснив, что по этому знаку найдутся люди, которые вознаградят его. И на самом деле, через некоторое время один из путешествующих пифагорейцев заметил звезду и стал расспрашивать хозяина дома о том, каким образом она появились у входа. После рассказа хозяина гость щедро вознаградил его. Пентаграмма была хорошо известна и в Древнем Египте. Но непосредственно как эмблема здоровья она была принята лишь в Древней Греции. В настоящее время существует гипотеза, что пентаграмма – первичное понятие, а «золотое сечение» вторично. Пентаграмму никто не изобретал, ее только скопировали с натуры. Вид пятиконечной звезды имеют пяти лепестковые цветы плодовых деревьев и кустарников, морские звезды. Те и другие создания природы человек наблюдает уже тысячи лет. Поэтому естественно предположить, что геометрический образ этих объектов – пентаграмма – стала известна раньше, чем «золотая» пропорция. 3.5 Спираль Архимеда Последовательно отсекая от золотых прямоугольников квадраты до бесконечности, каждый раз соединяя противоположные точки четвертью окружности, мы получим довольно изящную кривую. Первым внимание на неё обратил древнегреческий ученый Архимед, имя которого она и носит. Он изучал её и вывел уравнение этой спирали (Рис.7). 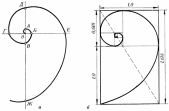 Рисунок 7. Спираль Архимеда. В настоящее время спираль Архимеда широко используется в технике. 4 Ряд Фибоначчи С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр: Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Это отношение обозначается символом Ф. Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему. Фибоначчи так же занимался решением практических нужд торговли: с помощью какого наименьшего количества гирь можно взвесить товар? Фибоначчи доказывает, что оптимальной является такая система гирь: 1, 2, 4, 8, 16... 5 Золотые пропорции в природе В биологических исследованиях было показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем. Было установлено, что числовой ряд чисел Фибоначчи характеризует структурную организацию многих живых систем. Например, винтовое листорасположение на ветке составляет дробь (число оборотов на стебле/число листьев в цикле, напр. 2/5; 3/8; 5/13), соответствующую рядам Фибоначчи. Хорошо известна "золотая" пропорция пяти лепестковых цветков яблони, груши и многих других растений. Носители генетического кода - молекулы ДНК и РНК - имеют структуру двойной спирали; ее размеры почти полностью соответствуют числам ряда Фибоначчи. Гете подчеркивал тенденцию природы к спиральности. Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Гете называл спираль "кривой жизни". Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках "упакованы" по логарифмическим ("золотым") спиралям, завивающимся навстречу друг другу, причем числа "правых "и "левых" спиралей всегда относятся друг к другу, как соседние числа Фибоначчи. Рассмотрим побег цикория (Рис.8). От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс.  Рисунок.8 Побег цикория. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения. У многих бабочек соотношение размеров грудной и брюшной части тела отвечает золотой пропорции. Сложив крылья, ночная бабочка образует правильный равносторонний треугольник. Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2,3,5,8. Стрекоза также создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста. В ящерице длина ее хвоста так относится к длине остального тела, как 62 к 38 (Рис.9). 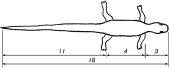 Рисунок 9. Ящерица. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Цейзинг измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. 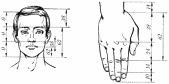 Рисунок 10. Золотые пропорции в теле человека. Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской.  Переходя к примерам золотого сечения в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды». Портрет Монны Лизы (Джоконды) (Рис.12) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника.  Рисунок 12. Портрет Монны Лизы (Джоконды) 8 Золотое сечение в архитектуре Ярким примером применения золотого сечения в архитектуре является церковь Покрова Богородицы на Нерли, возведенная в 1165 году (Рис.13).  Рисунок 13. Церковь Покрова Богородицы на Нерли. Еще одним примером, являются всемирно известные египетские пирамиды Хеопса (Рис.14).  Рисунок 14. Пирамиды Хеопса. Широко известны медицинские свойства пирамид, особенно золотого сечения. По некоторым наиболее распространенным мнениям, комната, в которой находится такая пирамида, кажется больше, а воздух - прозрачнее. Сны начинают запоминаться лучше. Заключение Иоанну Кеплеру, жившему пять веков назад, принадлежит высказывание: "Геометрия обладает двумя великими сокровищами. Первое - это теорема Пифагора, второе - деления отрезка в крайнем и среднем отношении" Необходимо сказать, что золотое сечение имеет большое применение в нашей жизни. Благодаря золотому сечению был открыт пояс астероидов между Марсом и Юпитером – по пропорции там должна находиться ещё одна планета. На летательных аппаратах с электромагнитными источниками энергии создаются прямоугольные ячейки с пропорцией золотого сечения. Итак, можно сделать выводы: во-первых, золотое сечение - это один из основных основополагающих принципов природы; во-вторых, человеческое представление о красивом явно сформировалось под влиянием того, какой порядок и гармонию человек видит в природе. Список использованных источников 1. Волошинов А.В. Математика и искусство. М., 1992. 2. Воробьев Н.Н. "Числа Фибоначчи" - М.: Наука 1964 3. Гарднер М. Математические головоломки и развлечения. М., 1994. 4. Журнал "Наука и техника" 5. Мурадова Р. Обобщающий урок по теме «Золотое сечение».// Математика (Приложение к газете «Первое сентября»).- 1999. № 1. 6. Прохоров А.И. Золотая спираль // Квант. 1984. № 9. 7. Информация из интернета: http://www.trinitas.ru/rus/doc/0232/004a/02321037.htm http://www.trinitas.ru/rus/002/a0232004.htm http://tolouaz.h17.ru/Path-ZS/Metaphisica-2.htm |
