клетеник. 38. Общее уравнение плоскости. Уравнение плоскости, проходящей через данную точку и имеющей данный нормальный вектор

• Название: 38. Общее уравнение плоскости. Уравнение плоскости, проходящей через данную точку и имеющей данный нормальный вектор
• Анкор: клетеник
• Дата: 27.11.2022
• Размер: 44.5 Kb.
• Имя файла: kletenik_38.doc
• Тип: Документы; #814196

§ 38. Общее уравнение плоскости. Уравнение плоскости,

проходящей через данную точку и имеющей данный

нормальный вектор
В декартовых координатах каждая плоскость определяется уравнением первой степени и каждое уравнение первой степени определяет плоскость.

Всякий (не равный нулю) вектор, перпендикулярный к данной плоскости, называется её нормальным вектором. Уравнение

А(х — x_о) + В(у — y_о) + С(z — zz₀) = 0 (1)

определяет плоскость, проходящую через точку М₀(х₀; у₀; z₀) и имеющую нормальный вектор п = {А; В; С}.

Раскрывая в уравнении (1) скобки и обозначая число —Ах₀ — Ву₀,—Сz₀ буквой D представим его в виде:

Ах+ By + Cz + D = 0.

Это уравнение называется общим уравнением плоскости.

913. Составить уравнение плоскости, которая проходит через точку M₁(2; 1; —1) и имеет нормальный вектор n ={1, —2; 3}.

914. Составить уравнение плоскости, которая проходит через начало координат и имеет нормальный вектор п = {5; 0; —3}.

915. Точка Р (2; —1; —1) служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составить уравне­ние этой плоскости.

916. Даны две точки М₁(3; —1; 2) и М₂(4; —2; —1). Соста­вить уравнение плоскости, проходящей через точку М₁перпендику­лярно к вектору .

917. Составить уравнение плоскости, проходящей через точку M₁(3;4; —5) параллельно двум векторам a₁ = {3; 1; —1} и a₂ = {1; —2; 1}.

918. Доказать, что уравнение плоскости, проходящей через точку М₀(х₀;у₀;z₀) параллельно двум векторам

a₁ = {l₁; m₁; п₁;} и a₂ = {l₂; m₂; п₂;}

может быть представлено в следующем виде: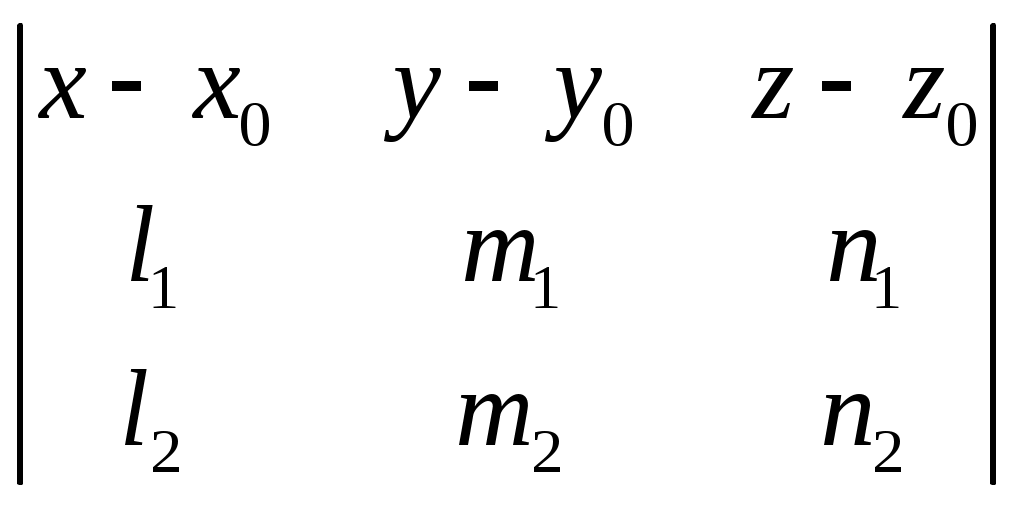

= 0

919. Составить уравнение плоскости, проходящей через точки M₁(2; — 1; 3) и М₂(3; 1; 2) параллельно вектору а = {3; — 1; —4}.

920. Доказать, что уравнение плоскости, проходящей через точки М₁(х₁;у₁;z₁) и М₂(х₂;у₂;z₂) параллельно вектору

а = {1; т;},

может быть представлено в следующем виде: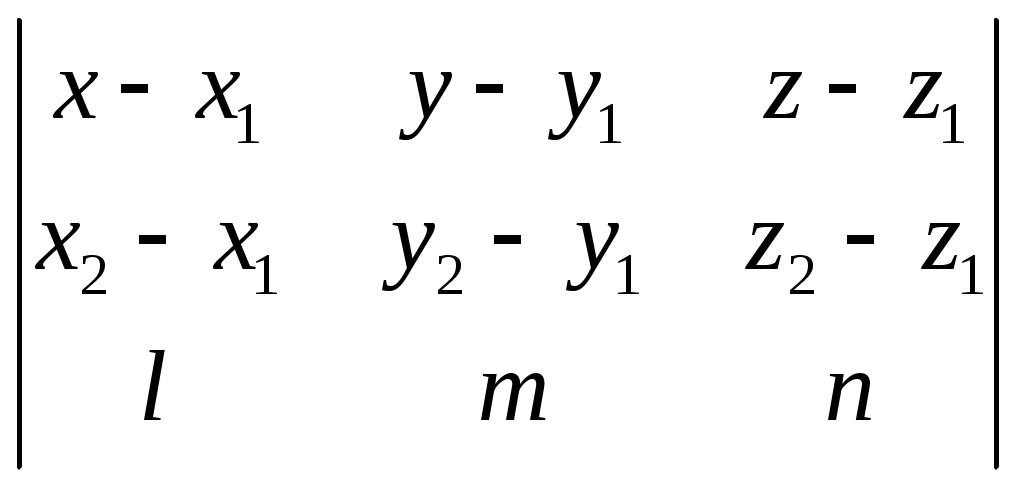

= 0

921. Составить уравнение плоскости, проходящей через три точки: М₁ (3; — 1; 2), М₂ (4; — 1; — 1) и М₃ (2; 0; 2).

922. Доказать, что уравнение плоскости, проходящей через три точки:

М₁(х₁;у₁;z₁) М₂(х₂;у₂;z₂) М₃(х₃;у₃;z₃)

может быть представлено в следующем виде: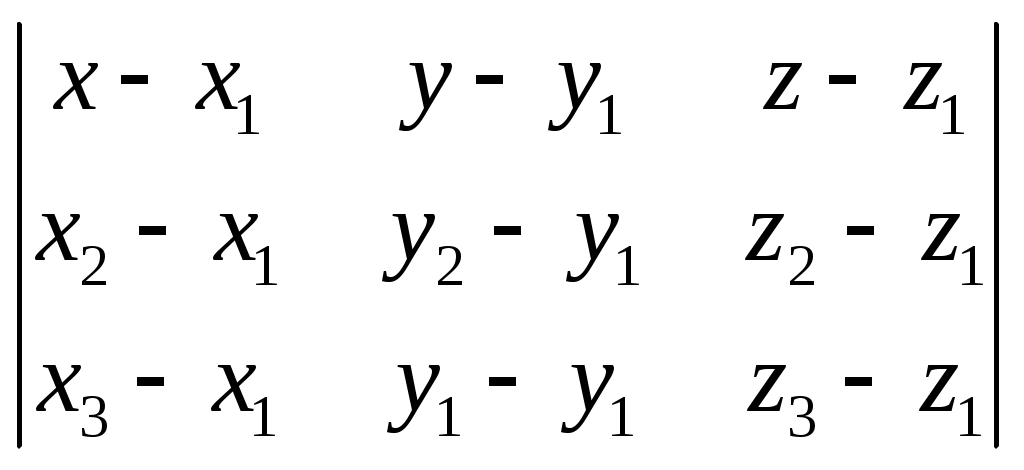

= 0

923. Определить координаты какого-нибудь нормального вектора каждой из следующих плоскостей. В каждом случае написать общее выражение координат произвольного нормального вектора:

1) 2х—у — 2z + 5 = 0; 2) х + 5у — z = 0;

3) 3х —2у —7 = 0; 4) 5у —3z = 0; 5)х + 2 = 0;

6) у — 3 = 0.

924. Установить, какие из следующих пар уравнений определяют параллельные плоскости:

1) 2х — 3у + 5z — 7 = 0, 2х — 3у + 5z + 3 = 0;

2) 4х+2у —4z + 5 = 0, 2х + у + 2z—1=0;

3) х—3z +2 = 0, 2х —6z — 7 = 0.

925. Установить, какие из следующих пар уравнений определяют перпендикулярные плоскости:

1) 3х—у — 2z — 5 = 0, х + 9у — 32 + 2 = 0;

2) 2х + 3у —2 —3 = 0, х — у — z + 5 = 0;

3) 2х —5у + z = 0, х + 22 —3 = 0.

926. Определить, при каких значениях l и m следующие пары уравнений будут определять параллельные плоскости:

1) 2х + lу + 3z — 5 = 0, mх —6у —6z + 2 = 0;

2) 3х— у + lz — 9 = 0, 2х + mу + 2z —3 = 0;

3) mx + 3у — 2z — 1=0, 2х— 5у — lz = 0.

927. Определить, при каком значении l следующие пары урав­нений будут определять перпендикулярные плоскости:

1) 3х — 5у+ lz — 3 = 0, х + 3у + 2z + 5 = 0;

2) 5х + у — 32 — 2 = 0, 2х + lу — 3z+ 1 = 0;

3) 7х — 2у — 2 = 0, lх + у — 3z — 1 = 0.

928. Определить двугранные углы, образованные пересечением следующих пар плоскостей:

1) х — у + z — 1 = 0, х + у —z + 3 = 0;

2) 3у — z = 0, 2у + z = 0;

3) 6х + 3у — 2z= 0, х + 2у + 6z — 12 = 0;

4) х + 2у + 2z — 3 = 0, 16х+12у — 15z — 1 = 0.

929. Составить уравнение плоскости, которая проходит через начало координат параллельно плоскости 5х — 3у + 2z — 3 = 0.

930. Составить уравнение плоскости, которая проходит через точку M₁(3; —2; —7) параллельно плоскости 2х — 3z + 5 = 0.

931. Составить уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям:

2х — у + 3z — 1=0, х + 2у + z = 0.

932. Составить уравнение плоскости, которая проходит через точку M₁(2; —1; 1) перпендикулярно к двум плоскостям:

2х — z + 1 = 0, у = 0.

933. Доказать, что уравнение плоскости, проходящей через точку М₀(х₀; у₀; z₀) перпендикулярно к плоскостям

А₁х + В₁у + С₁z + D₁ = 0, A₂x + В₂у + С₂z + D₂ = 0,

может быть представлено в следующем виде: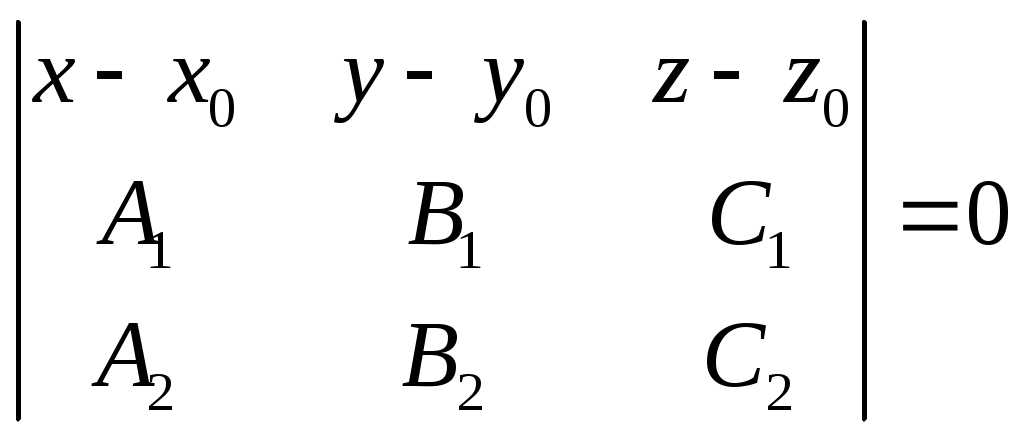

934. Составить уравнение плоскости, которая проходит через две точки М₁(1; —1; —2) и M₂(3; 1; 1) перпендикулярно к пло­скости х — 2у + 3z — 5 = 0.

935. Доказать, что уравнение плоскости, проходящей через две точки М₁(х₁; y₁; z₁) и M₂(x₂; у₂; z₂) перпендикулярно к плоскости

Ax + By + C2 + D = 0,

может быть представлено в следующем виде:

=0.

936. Установить, что три плоскости х — 2у + z— 7 = 0, 2х + у — z + 2 = 0, х—3y+2z—11 = 0 имеют одну общую точку, и вычислить еe координаты.

937. Доказать, что три плоскости 7х + 4y + 7z + 1 = 0, 2х — у — 2 + 2 = 0, х + 2у + 32 — 1 = 0 проходят через одну прямую.

938. Доказать, что три плоскости 2х — у + 3z— 5 = 0, 3х + у + 2z — 1 = 0, 4х + 3у + z + 2 = 0 пересекаются по трём различным параллельным прямым.

939. Определить, при каких значениях а и b плоскости 2х — у + 3z — 1 = 0, х + 2у — z + b = 0, х + ау —6z + 10 = 0:

1) имеют одну общую точку;

2) проходят через одну прямую;

3) пересекаются по трём различным параллельным прямым.