Контрольные вопросы по MATLAB. и Оператор
 Скачать 26.93 Kb. Скачать 26.93 Kb.
|
|
Вопросы на защиту: В чём отличия действия операторов «=», «=» и «→»? Оператор «=» предназначен для проверки равенства, подстановки переменной. Для символьного вычисления необходимо использовать оператор символьного преобразования «→», а для численного расчёта – оператор вычисления «=». Как можно уточнять действие оператора «→»? Ключевые слова и модификаторы дополнительных параметров преобразования находятся в группе инструментов «Символьные операции» на вкладке меню «Математика». Какие успешные и неуспешные исходы возможны в результате символьных преобразований? Как использовать блок решения? Блок решения имеет три части. В первой части («Начальные приближения») следует записать произвольные начальные значения неизвестных. Во второй части («Ограничения») должны быть записаны сами решаемые уравнения (здесь, как и всегда при описании уравнений, используется символ проверки равенства, а не обычный символ равенства). В третьей части («Решатель») следует вставить ключевое слово find, в скобках перечислить через запятую неизвестные, а после скобок добавить обычный символ равенства, обозначающий вычисление. После выполнения перечисленных действий в третьей части блока должно появиться найденное решение. Какие операции можно выполнять с матрицами и каким образом? Транспонирование матрицы можно выполнить, использовав оператор транспонирования  в меню «Матрицы/таблицы > Операторы с векторами/матрицами». в меню «Матрицы/таблицы > Операторы с векторами/матрицами».Для получения обратной матрицы достаточно выполнить обычное возведение в степень, при этом следует указать степень «-1». Нахождение определителя можно реализовать с помощью функции det в меню «Матрицы/таблицы > Функции с векторами/матрицами». Какие настройки можно изменять при выполнении разложения функции в ряд? Чтобы разложить функцию в окрестности точки, отличной от 0, следует указать после ключевого слова series значения переменной или переменных с помощью логического оператора равенства: 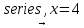 . .Чтобы возвращать определённое число членов ряда, необходимо указать это число через запятую после ключевого слова или после перечисления переменных:  Какие символьные преобразования можно выполнять с полиномами и каким способом? Выполнение преобразований происходит с использованием оператора символьного преобразования, сверху от которого следует указать дополнительные параметры преобразования: разложение полинома на множители: 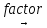 ; ;подстановка переменной:  ; следует обратить внимание на знак равенства, используемый в подстановке; ; следует обратить внимание на знак равенства, используемый в подстановке;разложение выражения по степеням полинома: 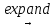 ; ;приведение подобных слагаемых по некоторой переменной:  . .Какие положительные и отрицательные стороны имеет использование математических программных пакетов при выполнении символьных вычислений (аналитических расчётов)? Основное преимущество пакета – естественный математический язык, наглядность, высокая точность вычислений, реализация многих стандартных функций вычислительной математики, возможность символьных математических преобразований. Недостатками являются ограниченные возможности операторов, трудности реализации сложных алгоритмов. Вопросы на защиту: Какие основные настройки параметров шрифта можно выполнить в системе MATLAB? Можно изменить гарнитуру, начертание и размеры шрифтов в различных компонентах системы. К каким последствиям может привести неудачная настройка режима копирования изображений? Ответ обосновать. Копирование изображения может происходить не всегда корректно и не всегда с желаемым качеством. Поэтому иногда приходится подбирать настройки, определяющие формат, в котором должно происходить копирование изображений в буфер обмена, а именно формат изображения (Metafile, Preserveinformation, Bitmap), фон изображения и размер изображения. Почему установка текущего каталога является важным шагом настройки рабочей среды MATLAB? Текущий каталог имеет важное значение для запуска M-файлов, для вызова функций и для работы с сохранёнными данными.Текущий каталог должен быть предварительно создан в доступном для редактирования месте на рабочем диске, после чего выбран в качестве текущего в системе MATLAB. Какую пользу даёт отображение номеров строк в редакторе? Отображение номеров строк при редактировании программного кода в редакторе позволяет упростить навигацию по программе в случае больших объёмов кода, облегчить поиск ошибок и совместное обсуждение программного кода. Какие варианты описания векторов и матриц существуют? Первый способ: Чтобы хранить матрицы, надо использовать двумерный массив. Предположим, что надо ввести матрицу  . .Для этого необходимо набрать >>A = [2 -3 5; 3 4 1] Второй способ: Пусть требуется написать следующую матрицу: 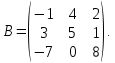 . .Начните набирать в командной строке >> B = [-1 4 2 Нажмите клавишу 3 5 1 -7 0 8] Третий способ: Например, матрицу A можно ввести при помощи команды:>> A = [[2; 3] [-3; 4] [5; 1]] Другие способы задания матриц и векторов:
Как получить часть матрицы, состоящую из значений, которые лежат в этой матрице разрозненно (например, из матрицы размера 3×3 извлечь только элементы (1,1), (3,1), (1,3), (3,3))? Для обращения к элементам матриц следует указать после имени матрицы индексы элементов в круглых скобках. Примеры:
Чем отличаются матричные и поэлементные операции? Почему важно следить за типом операции? К матричным действиям с матрицами относятся такие операции, которые используются в матричном исчислении в математике. Базовые действия с матрицами (векторами): сложение, вычитание, транспонирование, умножение матрицы на число, умножение матрицы на матрицу, возведение квадратной матрицы в степень – осуществляются в MATLAB с помощью обычных знаков арифметических операций. Условия, при которых эти операции возможны, таковы: при сложении или вычитании матриц они должны иметь одинаковые размеры; при умножении матриц число столбцов первого множителя должно совпадать с числом строк второго множителя. Невыполнение этих условий приводит к появлению сообщения об ошибке. Поэлементные действия с матрицами не являются операциями линейной алгебры, они лишь преобразуют элементы матрицы как элементы обычного двумерного массива. Кроме поэлементного преобразования матриц с помощью математических функций, в MATLAB можно выполнять поэлементные преобразования матриц с помощью арифметических операций. К таким операциям относятся операции поэлементного умножения с помощью оператора <.*>(без пробела между точкой и звездочкой), поэлементного деления <./>, обратного поэлементного деления <.\>, поэлементного возведение в степень <.^>. Операции поэлементного преобразования матриц могут выполнятся только над матрицами одинакового размера и типа. В результате получается матрица такого же размера и типа. Следует соблюдать осторожность при записи математических операций для векторов и матриц, поскольку пропущенная или, напротив, добавленная лишний раз точка может приводить к совершенно некорректным результатам или прерыванию расчётов. В файлы каких форматов можно осуществлять сохранение данных в системе MATLAB? Стандартным форматом файлов для сохранения данных является двоичный формат MAT. В интерактивном режиме можно сохранить значения переменных и в виде текстового M-файла. Почему во многих случаях перед запуском вычислительного эксперимента следует очистить рабочую область? Как это сделать? В ходе расчётов важно следить за состоянием рабочей области. Существует довольно высокая вероятность того, что при проведении серии вычислительных экспериментов данные, полученные в ходе предыдущего эксперимента, повлияют на расчёты в рамках следующего эксперимента. Ещё одна потенциально опасная ситуация – нехватка памяти в ходе расчётов. Для того, чтобы предупредить возникновение таких ситуаций, можно использовать команду clear. Для очистки всей рабочей области следует выполнить команду clear без параметров или же команду clear all. Добавлять эту команду обычно необходимо в самое начало цепочки команд очередного вычислительного эксперимента. Согласно документации, команда clear all является более ресурсоёмкой, поскольку уничтожает не только переменные в рабочей области, но и все загруженные в память определения функций, классов, глобальных переменных и некоторую другую информацию. Уничтожение отдельных переменных можно выполнить, перечислив через пробел их имена в команде clear, например следующим образом: clear a mat1 B1. Такое уничтожение желательно делать, когда в ходе расчёта обрабатываются большие объёмы данных, и при этом необходимость в каких-то переменных отпадает. В чём состоят преимущества режима вычислений на основе М-файлов от интерактивного режима в командном окне? Решение большинства задач научных и инженерных расчётов требует выполнения длинных цепочек вычислений и преобразований данных, зачастую с циклическими и ветвящимися алгоритмами. Очевидно, что в подобных случаях командный режим MATLAB является крайне неудобным и неэффективным в плане трудоёмкости решения задач. Более правильной альтернативой служит описание сценариев (скриптов) на языке MATLAB в виде M-файлов. Где отображаются ошибки в случае их возникновения в процессе вычислений? В случае возникновения ошибок, сообщения о них будут появляться в командном окне. Вопросы на защиту: Какой ключевой подход лежит в основе расчёта и визуализации функций от одной переменной? Чтобы построить график, нужно знать координаты точек этого графика. Нанеся эти точки на координатную плоскость, можно соединить их линиями, тем самым получив желаемую визуализацию функции. Поэтому исходные данные для команд построения графиков должны являться таблицами чисел. Какой ключевой подход лежит в основе расчёта и визуализации функций от двух переменных? Чтобы понять принцип вычисления функций от двух переменных, необходимо представить себе, что это происходит для таблицы, каждый столбец которой соответствует определенному значению одного параметра функции, а каждая строка – другого. При построении графиков первому из параметров будет соответствовать ось абсцисс, а второму – ось ординат. При этом увеличение ординаты происходит в сторону увеличения номера строки. Можно ли построить график функции от одной переменной, если первым аргументом функции plot() будет являться вектор-столбец, а вторым – вектор-строка? Можно при условии, что вектора будут одинаковой длины. Почему перед построением графика рекомендуется выполнять открытие нового графического окна? Всегда ли это необходимо делать? Если перед вызовом функции построения графика существовали открытые графические окна, график будет отражен в том из них, которое было активно последним. В результате может произойти удаление имевшегося содержимого такого окна, что желательно далеко не всегда. Поэтому лучше предварить построение графика явным созданием графического окна. Почему рекомендуется подписывать оси и названия графиков? Какие средства MATLAB для этого предназначены? В подавляющем большинстве случаев корректная интерпретация графиков, их обсуждение с другими людьми, публикация в отчётах и статьях, представление в докладах будут затруднены при отсутствии обозначений осей координат. В зависимости от ситуации на графиках могут потребоваться и другие обозначения и комментарии, и MATLAB позволяет их добавить. Но в первую очередь должны быть однозначно обозначены именно координатные оси. Для этого следует использовать функции xlabel(), ylabel(), zlabel(). Каков принцип действия функции meshgrid()? Может ли она быть использована для вычисления и визуализации функций от одной переменной? Функция [X,Y]=meshgrid(x,y) формирует массивы X и Y, которые определяют координаты узлов прямоугольника, задаваемого векторами x и y. Этот прямоугольник задает область определения функции от двух переменных, которую можно построить в виде 3D-поверхности. Функция не может быть использована для визуализации функций от одной переменной. Можно ли строить графики функций от одной переменной, не передавая графическим функциям значения по оси абсцисс? Можно ли строить графики функций от двух переменных, не передавая графическим функциям значения по осям абсцисс и ординат? 1. Можно, вдоль оси абсцисс будут показаны значения в диапазоне, определяемом количеством элементов в векторе у. 2. Нельзя. Каким образом в одном графическом окне можно построить несколько графиков в разных системах координат? Если в одном графическом окне необходимо изобразить несколько графиков разных типов на нескольких координатных плоскостях, следует воспользоваться функцией subplot(). При её работе предполагается, что графическое окно разбивается на ячейки в виде сетки, а очередное построение графика будет происходить в одну из этих ячеек. Зачем необходимо добавлять комментарии в программный код? Каким образом это сделать в программе на языке MATLAB? Комментарии в MATLAB можно добавлять после символа «%». Они позволяют упростить понимание кода и дальнейшее его сопровождение. Вопросы на защиту: 1. Какие системные ресурсы являются ключевыми для большинства программ? Почему это так? Решение вычислительных задач зачастую является довольно ресурсоёмким процессом. В первую очередь это касается таких ресурсов как процессорное время и оперативная память. В зависимости от конкретной задачи повышенные потребности в системных ресурсах могут проявляться в заметном увеличении времени расчётов и (или) аварийном завершении вычислений из-за нехватки памяти. 2. Как в системе MATLAB происходит динамическое увеличение размера матрицы? Каковы побочные эффекты такой процедуры в плане использования системных ресурсов? Одним из способов уменьшения критичности данной проблемы является использование операторов цикла, например, следующим образом (слева указаны номера строк): x=0:0.1:99.9; y=0:0.05:49.95; for i=1:length(y) for j=1:length(x) Z(i,j)=sin(x(j))*cos(y(i)); end end Вычисление результата не требует вспомогательных матриц, то есть экономия памяти составит 15,3 МБ. Но ценой использования такого подхода является замедление работы программы. Работа с матрицей в операторах цикла в подавляющем большинстве случаев происходит медленнее, чем оперирование матрицами целиком. 3. Что такое разреженные матрицы? Как их создать и как с ними работать? В каких случаях использование разреженных матриц является эффективным? Разрежённая матрица — это матрица с преимущественно нулевыми элементами. Функция spconvert используется для создания разреженных матриц из простых разреженных форматов, легко производимых вне средств MATLAB: · S = spconvert(D) – преобразует матрицу D со строками, содержащими [i.j.r], где i – индекс ряда, j – индекс строки, г – численное значение, в соответствующую разреженную матрицу 4. Какие способы предварительного выделения памяти существуют в MATLAB()? Всегда ли они позволяют получить эффективный в плане использования системных ресурсов код? Выделить память под матрицу можно несколькими способами: − до манипуляций с матрицей задать какое-либо значение элементу с максимальными индексами по каждой из размерностей «Z(length(y), length(x))=0;»; − изменять переменные цикла, используемые как индексы элементов матриц, начиная с максимально возможных значений «for i=length(y):-1:1» и «for j=length(x):-1:1»; − создавать предварительно матрицу с помощью подходящей функции создания матриц специального вида, например, матриц нулей, матриц единиц, единичных матриц и тому подобных «Z=zeros(length(y),length(x));». Когда мы заранее знаем конечный размер матрицы, то все вычисления происходят для уже существующих ячеек памяти, и никакого многоэтапного процесса увеличения размера матрицы не требуется. 5. Поясните и проиллюстрируйте с помощью расчётов, как связаны данные во втором и третьем столбцах таблицы 1? Однако для многих задач такая точность представления чисел (15 знаков после запятой) является излишней. Зачастую можно ограничиться меньшей точностью без заметного ущерба решению задачи. А в некоторых задачах вообще хватает работы с целочисленными значениями. Поэтому при разработке программы можно использовать функции, изменяющие тип значений переменных. Можно заметить, что переход к расчётам с менее затратными для памяти типами данных позволит не только сократить потребности в системных ресурсах, но и в каких-то случаях повысить точность расчётов или же увеличить скорость работы программы. 6. В каких случаях переход к расчётам с менее затратными для памяти типами данных может позволить сократить потребности в системных ресурсах, повысить точность расчётов или жеувеличить скорость работы программы? Когда в задачах не нужна особая точность или когда в задачах можно ограничиться работой с целочисленными типами данных. 7. Какими способами в MATLAB можно оценить время работы программного кода? Время работы программы или её части можно определить с помощью функций tic() и toc(). Первая начинает отсчёт времени, а вторая замеряет прошедшее после начала отсчёта время. 8. Каково назначение профилировщика? Пояснить по материалам отчёта, какую информацию можно получить в результате профилирования и как её можно использовать. Он позволяет собирать статистическую информацию о выполняемых сценариях и функциях и представлять её в виде отчёта с разной степенью подробности и с выделением фрагментов кода, критичных с точки зрения эффективности их работы. Из подробного отчёта профилировщика можно быстро узнать время, затраченное на выполнение каждой из строчек кода, количество вызовов каждой из строчек, подсказку о возможности совершенствования некоторых строк для уменьшения времени работы кода, а также некоторую другую информацию. Профилирование крупных программ позволяет довольно быстро находить участки медленно работающего или неэффективно написанного кода, исправлять их и получать программный код, работающий на порядки быстрее своего начального варианта. 9. Что такое фрагментация памяти и какими способами можно её уменьшить или исключить? Фрагментация - это наличие большого числа несмежных участков свободной памяти очень маленького размера (фрагментов). Настолько маленького, что ни одна из вновь поступающих программ не может поместиться ни в одном из участков, хотя суммарный объем фрагментов может составить значительную величину, намного превышающую требуемый объем памяти. Clear all, Close all, pack |
