Системы координат, применяемые в динамике полета
 Скачать 2.85 Mb. Скачать 2.85 Mb.
|
1 2 Система уравнений движения ЛА является сложной нелинейной системой дифференциальных уравнений. Основным методом исследования таких уравнений является из интегрирование с помощью ЦВМ. В то же время при проектировании системы управления имеется настоятельная необходимость аналитического представления динамических и кинематических характеристик ЛА. Поэтому используют различные методы упрощения уравнений движения, что делает доступным аналитические методы исследования динамики полета. Одним из таких упрощений является линеаризация этих уравнений относительно малых отклонений параметров движения. Параметры возмущенного движения обычно определяют методами численного интегрирования с помощью ЦВМ как известные функции времени: Параметры возмущенного движения отличаются от параметров невозмущенного движения на некоторую малую величину: 1. С целью упрощения получаемых линеаризованных уравнений, учитывая, что в невозмущённом движении углы 2. Будем считать, что изменения массы в возмущенном и в невозмущенном движениях одинаковы и являются известными функциями времени. 3. Предполагаем также, что в невозмущенном движении кинематические параметры бокового движения 4. При упрощении геометрических соотношений между отклонениями С учётом этих предположений, а также выражений (17) будем считать, что силы и моменты, входящие в правые части уравнений (1) – (16), зависят от следующих параметров [5]: 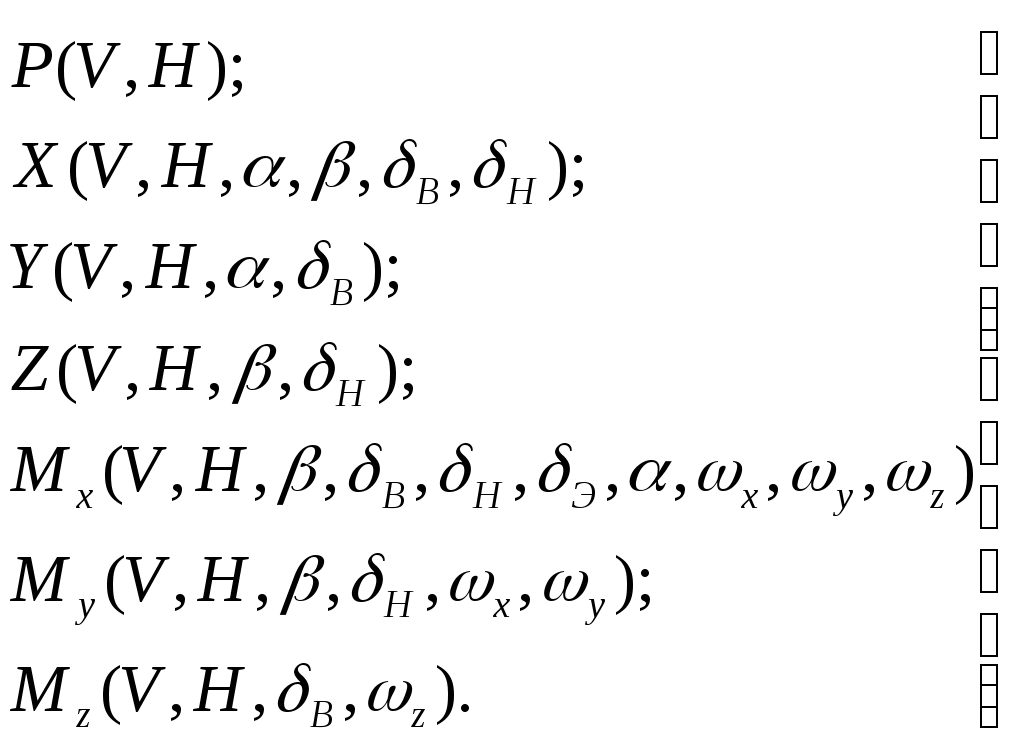 (19) (19)Проведем линеаризацию напримере уравнения (1): Придадим параметрам V, H, 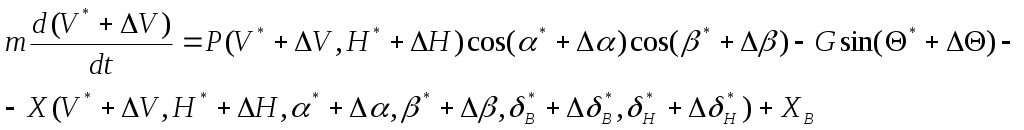 Разложим все функции в последнем уравнении в ряд Тейлора по степеням приращений 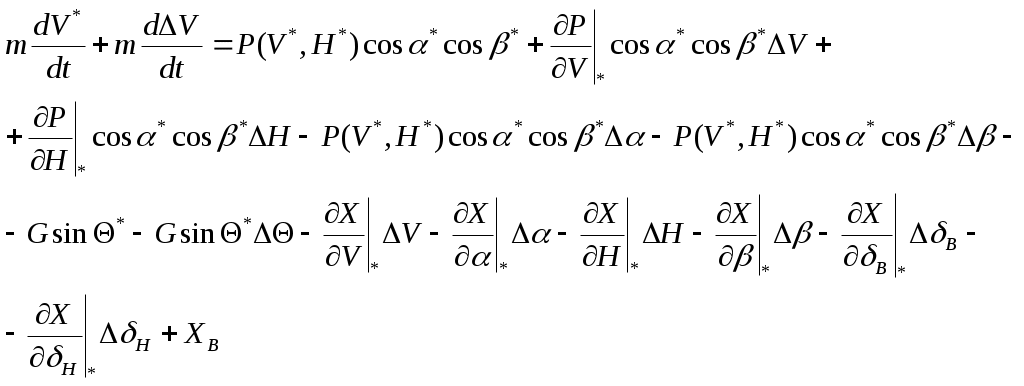 Для невозмущённых слагаемых в левой и правой частях уравнение (1) справедливо как тождество, поэтому линеаризованное уравнение возмущенного движения принимает вид 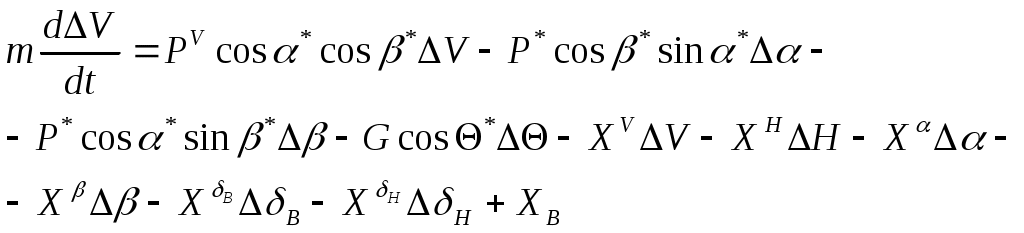 Так как в силу ранее принятых допущений произведения Опуская при записи индекс "*": 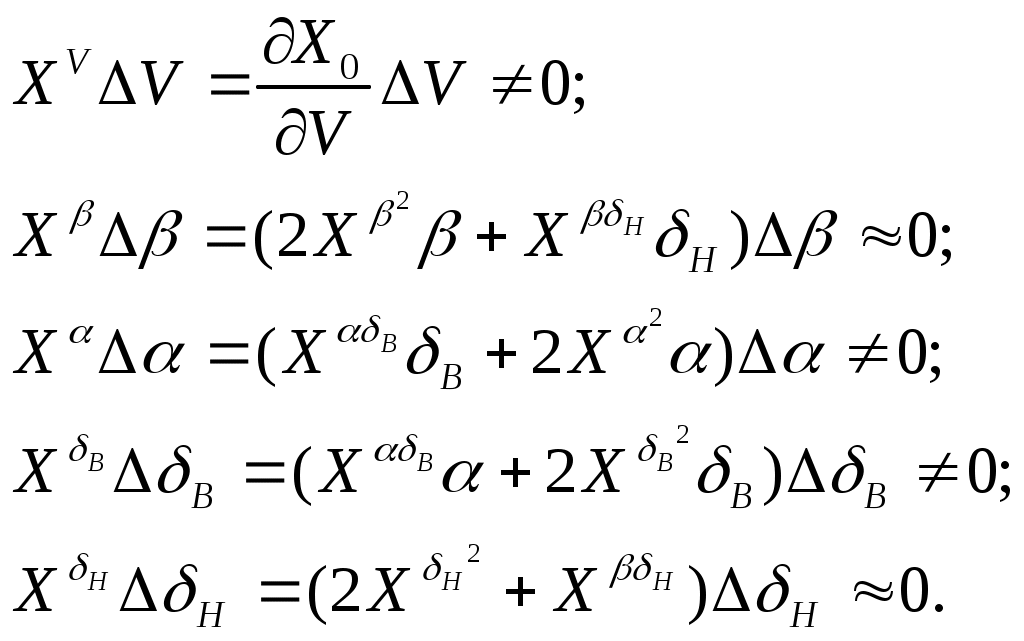 Таким образом, необходимо найти выражения для Известно [5, 4], что a – скорость звука, зависящая от высот полета; S – характерное сечение: В [5, 4] дается физическое толкование и математические выражения для всех аэродинамических сил и моментов. Тогда Обозначив Коэффициенты Аналогично вычисляются и другие производные. Тогда окончательно первое уравнение с ил получим в следующем виде: При линеаризации уравнения (2) отбрасывается член Уравнение (3) после линеаризации примет такой вид: В этом уравнении отброшены члены, содержащие произведения малых величин: Пример линеаризации четвертого уравнения Уравнение возмущенного движения примет следующий вид: На основании (19) можно раскрыть вариацию 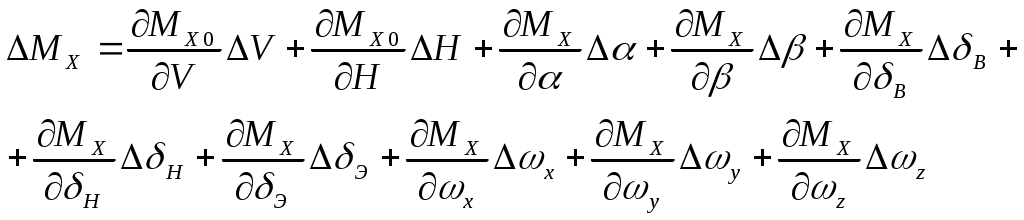 Величины Запишем линеаризованное уравнение (4): Аналогично линеаризуем уравнение (5) и (6): 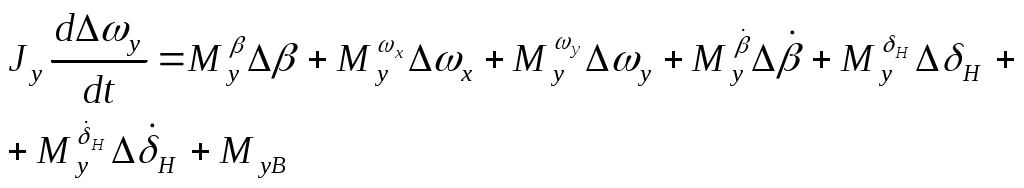 (5л) (5л)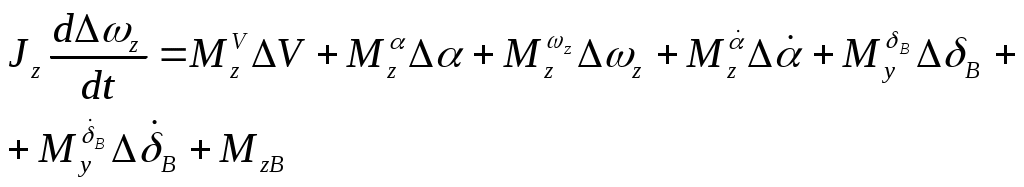 (6л) (6л)Разложение в ряд Тейлора уравнений (7), (8), и (9) относительно малых приращений параметров возмущенной траектории дает следующий результат: Линеаризуем геометрическое уравнение связи углов (10): После разложения в ряд Тейлора данное уравнение дает следующее соотношение между вариациями параметров: 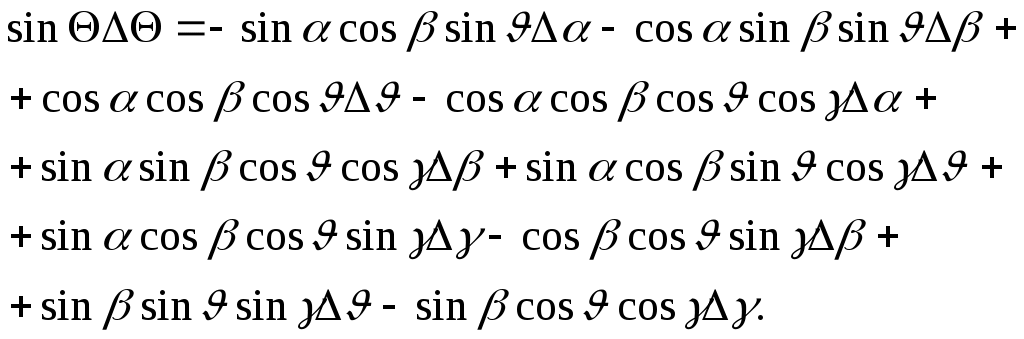 Отсюда с учетом допущений, сделанных в п.п. I – 4 данного параграфа, получаем: Уравнения (11) и (12) приводятся соответственно к виду Аналогично получаем линеаризованные кинематические уравнения (13)-(15) движения центра масс ЛА в земной системе координат: Уравнение (16) – линейно. Таким образом, получена линеаризованная система дифференциальных уравнений пространственного движения ЛА (1л) – (16л). Анализ динамических свойств ЛА как объекта управления осуществляется в динамике полета на основе именно этих уравнений. В качестве дальнейших шагов в упрощении линеаризованных уравнений движения ЛА применяют принцип «замороженных коэффициентов», что позволяет свести исходную систему к системе линейных уравнений с постоянными коэффициентами. И, наконец, проводят разделение уравнений движения на три независимые группы, которые характеризуют движение ЛА по каналу тангажа, курса и крена. Эти вопросы в данном пособии не рассматриваются. Полная система линеаризованных уравнений имеет вид: 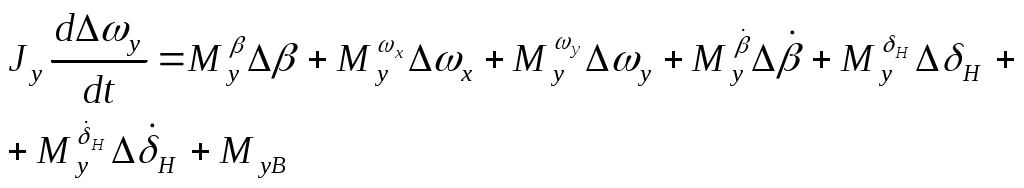 (5л) (5л)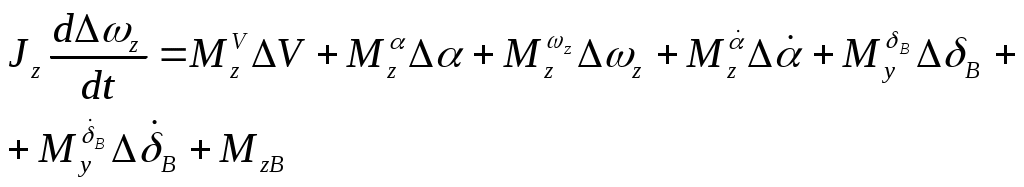 (6л) (6л)ЛИТЕРАТУРА Горбатенко С. А. и др. Расчет и анализ движения летательных аппаратов. – М.: Машиностроение, 1971. Горбатенко С. А. и др. Механика полета. Общие сведения. Уравнения движения. – М.: Машиностроение, 1969. Дмитриевский А. А. Внешняя баллистика. – М.: Машиностроение, 1972. Дмитриевский А. А. и др. Движение ракет (Введение в теорию полета ракет). – М.: изд. ВИМО, 1968. Лебедев А. А., Чернобровкин Л. С. Динамика полета беспилотных летательных аппаратов. – М.: Машиностроение, 1973. Микеладзе В. Г., Титов В. М. Основные геометрические и аэродинамические характеристики самолетов и ракет. – М.: Машиностроение, 1978. 1 2 |
