Системы координат, применяемые в динамике полета
 Скачать 2.85 Mb. Скачать 2.85 Mb.
|
1 2 Введение. При проектировании систем стабилизации и управления летательных аппаратов важным этапом является выявление динамических свойств летательного аппарата (ЛА) как объекта управления. Имеется обширная отечественная и зарубежная литература, посвященная построению математической модели динамики движения летательного аппарата. Настоящие методические указания облегчают работу с этой литературой, дают рациональные приемы вывода уравнений движения ЛА и их линеаризации. § 1. Системы координат, применяемые в динамике полета. Задачи динамики полета самолетов и ракет рассматриваются обычно в топоцентрической системе отсчета. Начало топоцентрической системы координат помещается в пункте наблюдения, в частности, на поверхности земного шара. Эта система используется в тех случаях, когда рассматривается движение по отношению к поверхности Земли. I. Земная система координат. Частный случай топоцентрической системы координат – земная система координат. Земных координат несколько. За начало земной системы прямоугольных координат можно принимать центр масс Земли, точку старта или другую неподвижную относительно Земли точку. Выберем земную систему координат следующим образом (рис. 1). 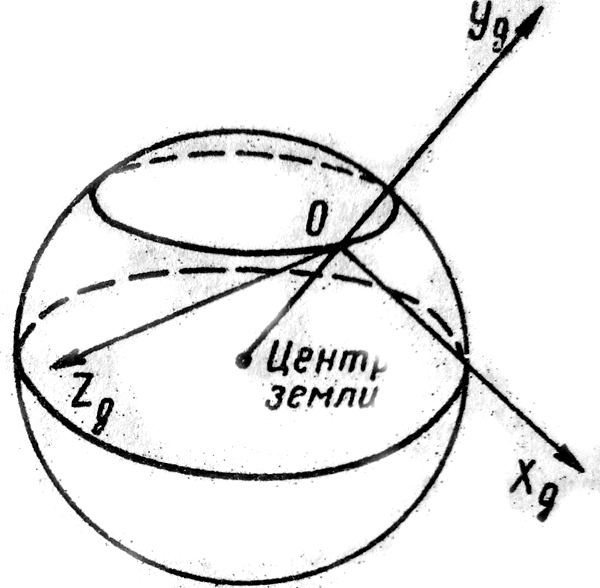 Рис. 1. Земная система координат Ось OYg – прямая, соединяющая центр Земли с точкой старта на её поверхности. Ось OXg перпендикулярна оси OYg и лежит в вертикальной плоскости прицеливания или начального движения ЛА в момент старта. Ось OZg дополняет систему до правой. Такая система координат называется нормальной земной системой координат OXgYgZg. Часто начало координат нормальной земной системы помещают в центре масс ЛА, а направление её осей совпадает с начальным направлением этих осей в момент старта. Таким образом, определяется нормальная система координат OXgYgZg, а её оси в данном случае совпадают также с осями стартовой системы OXcYcZc. В дальнейшем нормальную систему будем обозначать индексом g. Задав оси системы координат, можно выбрать базис, в котором любой вектор запишется так: где II. Связанная система координат Начало связанной системы координат (рис. 2) помещают в центре масс ЛА, который будем считать неподвижным относительно корпуса ЛА. Ось OX направлена вдоль строительной оси корпуса ЛА вперед. Ось OY располагают в той плоскости симметрии ЛА, которая в момент пуска совпадает с плоскостью стрельбы. Ось OY перпендикулярна оси OX и направлена вверх. Ось OZ дополняет систему до правой. Связанная система координат неподвижна относительно корпуса ЛА. Обозначать её будем индексом I. 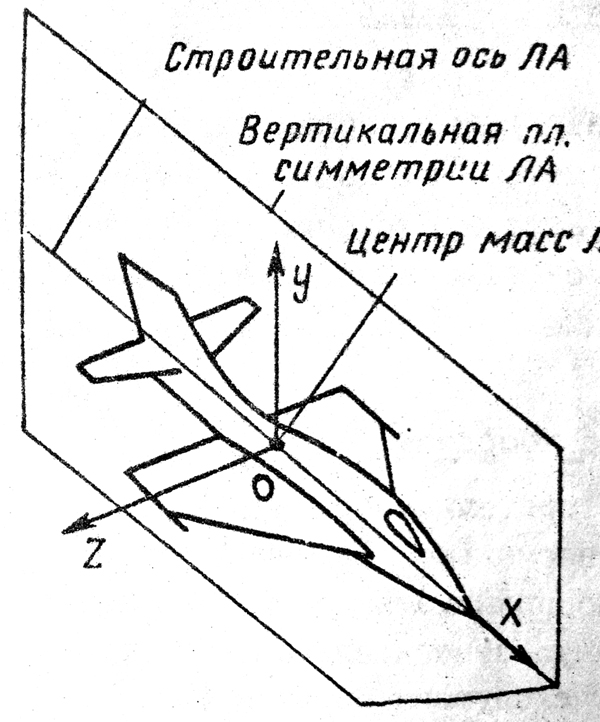 Рис. 2. Связная система координат III. Скоростная система координат В скоростной системе координат (рис. 3) ось OXa совпадает с направлением вектора скорости полёта центра масс ЛА и закреплена в центре масс, ось OYa перпендикулярна ей, лежит в вертикальной плоскости симметрии ЛА и направлена вверх. Ось OZa перпендикулярна осям OXa и OYa и дополняет их до правой тройки. Скоростую систему будем обозначать индексом a. IV. Траекторная система координат В траекторной системе координат (рис. 4) ось OXk, как и в скоростной, совпадает с направлением вектора скорости, ось OYk направлена перпендикулярно ей и лежит в местной вертикальной плоскости, ось OZk перпендикулярна первым двум, лежит в горизонтальной плоскости и направлена в сторону правого крыла. Траекторную систему обозначим индексом k. 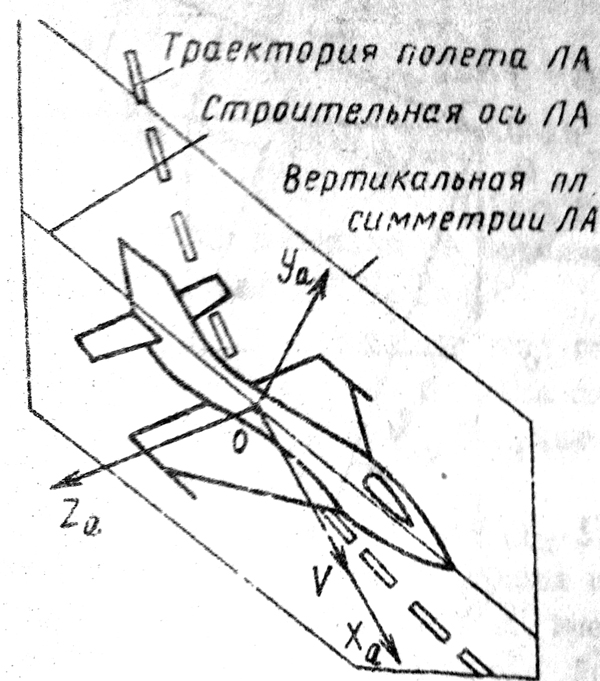 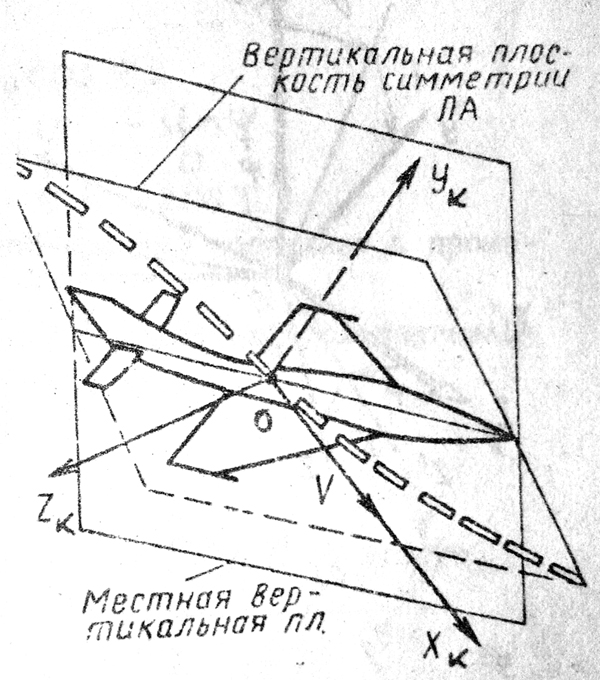 Рис. 3. Скоростная система координат Рис. 4. Траекторная система координат § 2. Связь между системами координат Определенные в § 1 системы координат являются ортогональными, поэтому переход из системы координат A в систему координат B характеризуется ортогональным преобразованием Для ортогональных матриц справедливо: 1. Как видно из рис. 5, связанная и нормальная системы связаны между собой через углы Эйлера. Обычно принимается следующий порядок поворота координатных осей. 1) Поворот вокруг оси OYg на угол 2) Поворот на угол 3) Поворот на угол 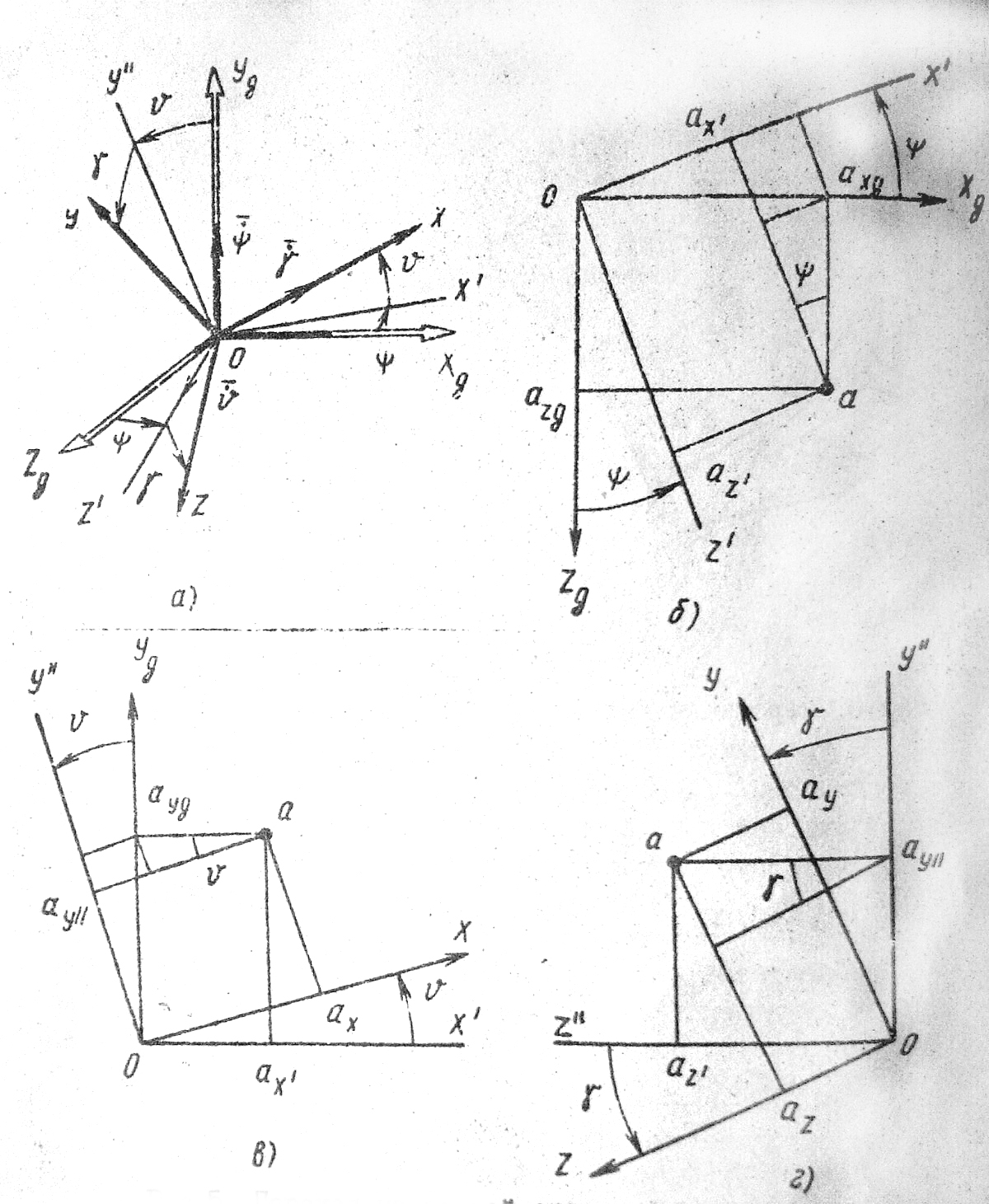 Рис. 5. Переход из земной системы координат в связанную. Найдем матрицу T(1,g) перехода из нормальной системы координат в связанную (рис. 5а). Первый поворот происходит в плоскости OXgYg на угол Таким образом, 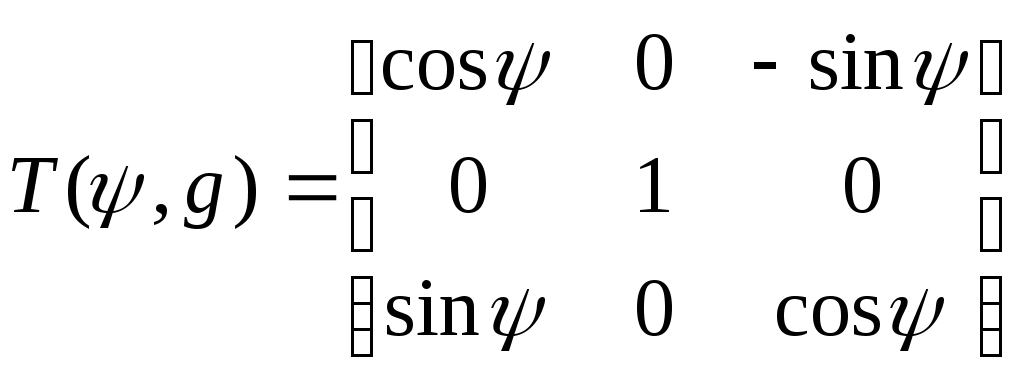 – это матрица перехода из нормальной системы координат в промежуточную систему OX'YgZ'. На рис. 5в иллюстрируется второй поворот на угол тангажа Таким образом, матрица перехода из системы OX'YgZ' во вторую промежуточную систему OXY''Z' имеет вид 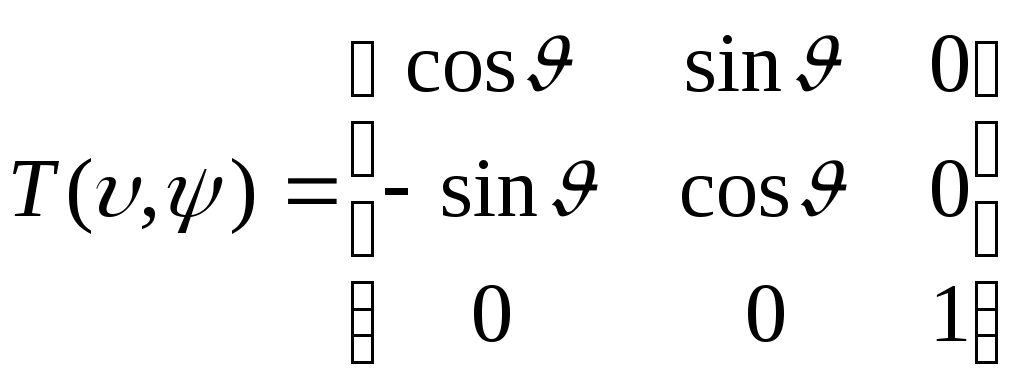 . .И, наконец, поворот на угол крена Матрица перехода из системы OXY''Z' в систему OXYZ имеет вид: 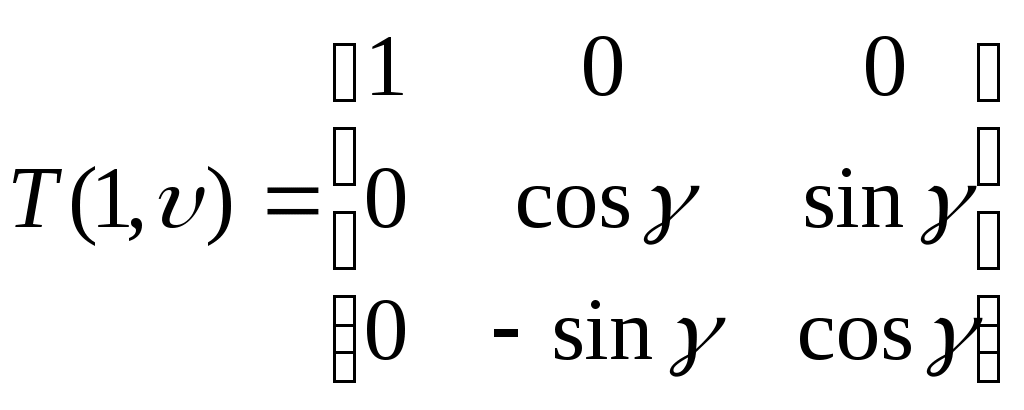 Найдем искомую матрицу: 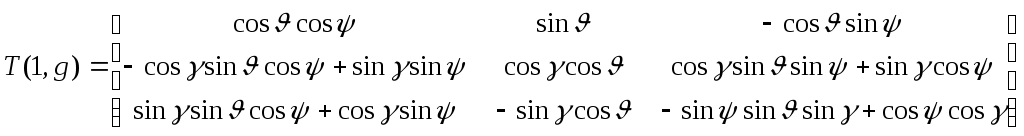 2. Скоростная и нормальная системы координат (рис. 6) связаны между собой через три угла Эйлера, которые перечислены в порядке последовательности поворотов: 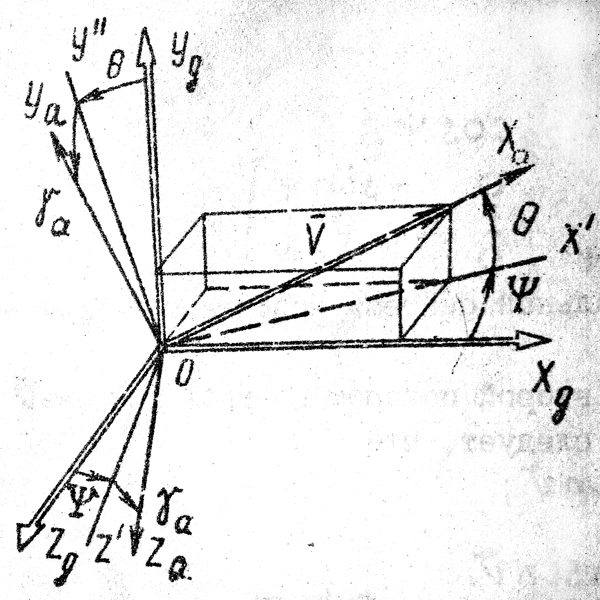 Рис. 6. Переход из нормальной системы координат в скоростную Нетрудно видеть, что матрицу перехода из нормальной системы координат в скоростную T(a,g) можно получить из известной уже матрицы T(1,g) путём соответственной замены углов 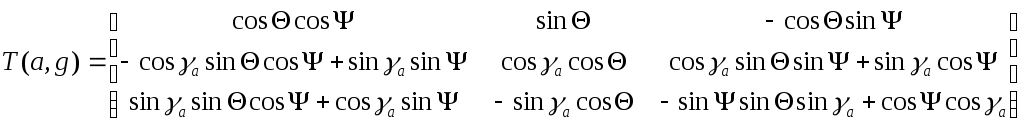 3. Траекторную систему координат можно получить из нормальной с помощью двух последовательных поворотов на углы Матрицу перехода из нормальной в траекторную систему координат T(k,g) можно получить из матрицы T(a,g), положив в ней 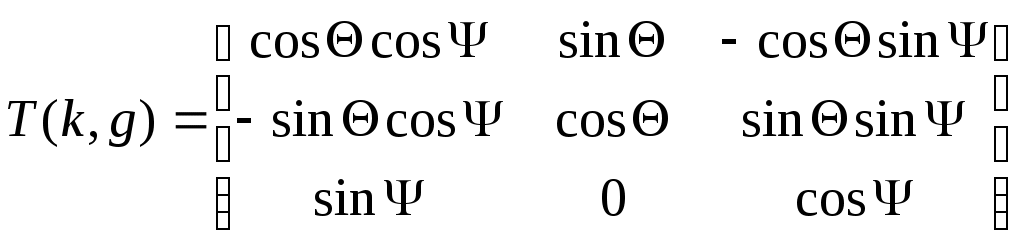 А матрицу перехода с траекторной системы к скоростной T(a,k) получим как матрицу третьего поворота на угол 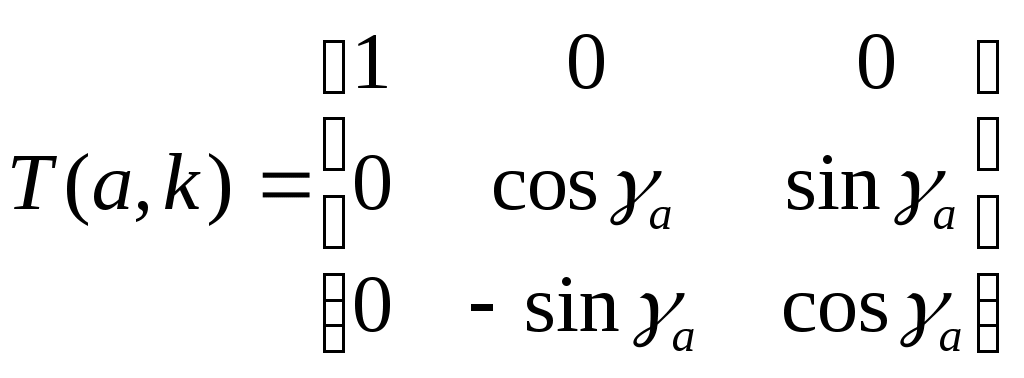 4. Связанная система координат может быть получена из скоростной системы координат с помощью двух последовательных поворотов – на углы 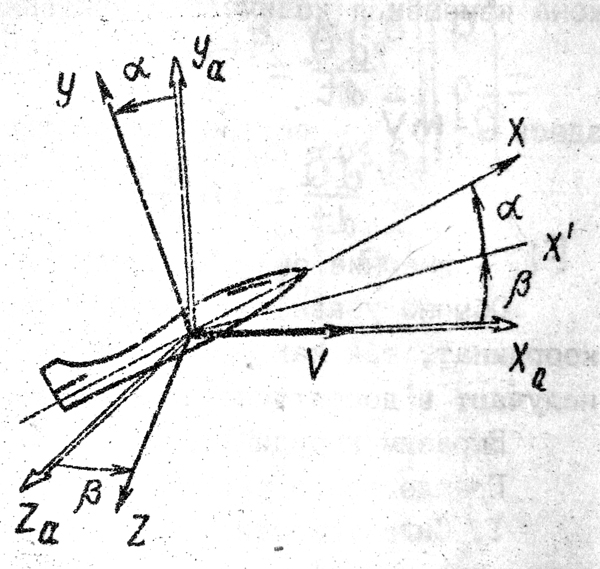 Рис. 7. Переход из скоростной системы в связанную Матрицу T(1,a) перехода из скоростной системы координат в связанную, запишем так же, как и матрицу T(k,g) перехода из нормальной системы в траекторную, заменив в последней углы 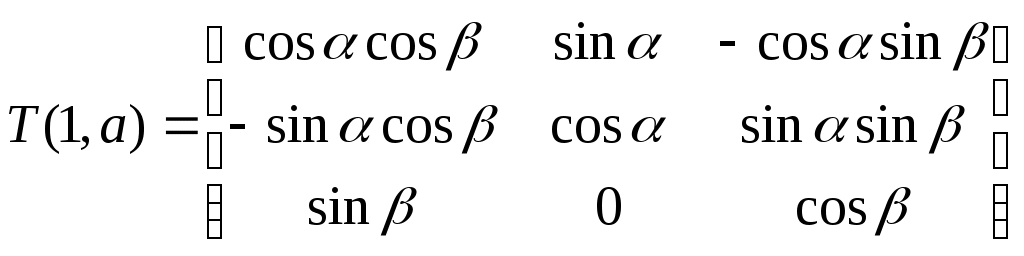 Подробная классификация систем координат и матриц перехода из одной системы в другую дана в [2]. В рекомендуемой литературе [1]-[5] все определения и обозначения даны в соответствии с ГОСТ 1075-41. Для облегчения перехода от системы обозначений ГОСТ 1075-41 к принятой в настоящее время системе ГОСТ 20058-74 следует пользоваться. § 3. Дифференциальные уравнения движения летательного аппарата При выводе уравнений движения ЛА делает следующие допущения: 1. ЛА рассматривается как абсолютно твёрдое тело переменной массы, имеющие 6 степеней свободы. 2. Моменты инерции ЛА постоянны. 3. ЛА имеет вертикальную плоскость симметрии. 3. Не учитываются влияние ветра, сферичность и вращение земли. Уравнения движения центра масс ЛА получим основании закона изменения количества движения центра масс: Здесь Fi – внешние силы, действующие на ЛА. Обычно уравнения сил проецируют на оси траекторной системы координат, так как в это случае Vx=V, Vy=Vz=0 и уравнения получают в достаточно простом виде. Выразим координаты всех сил в базисе траекторной системы. Прежде всего рассмотрим эти силы. 1. Сила тяжести. Поскольку эта сила направлена по местной вертикали, её обычно задают в базисе нормальной системы координат: 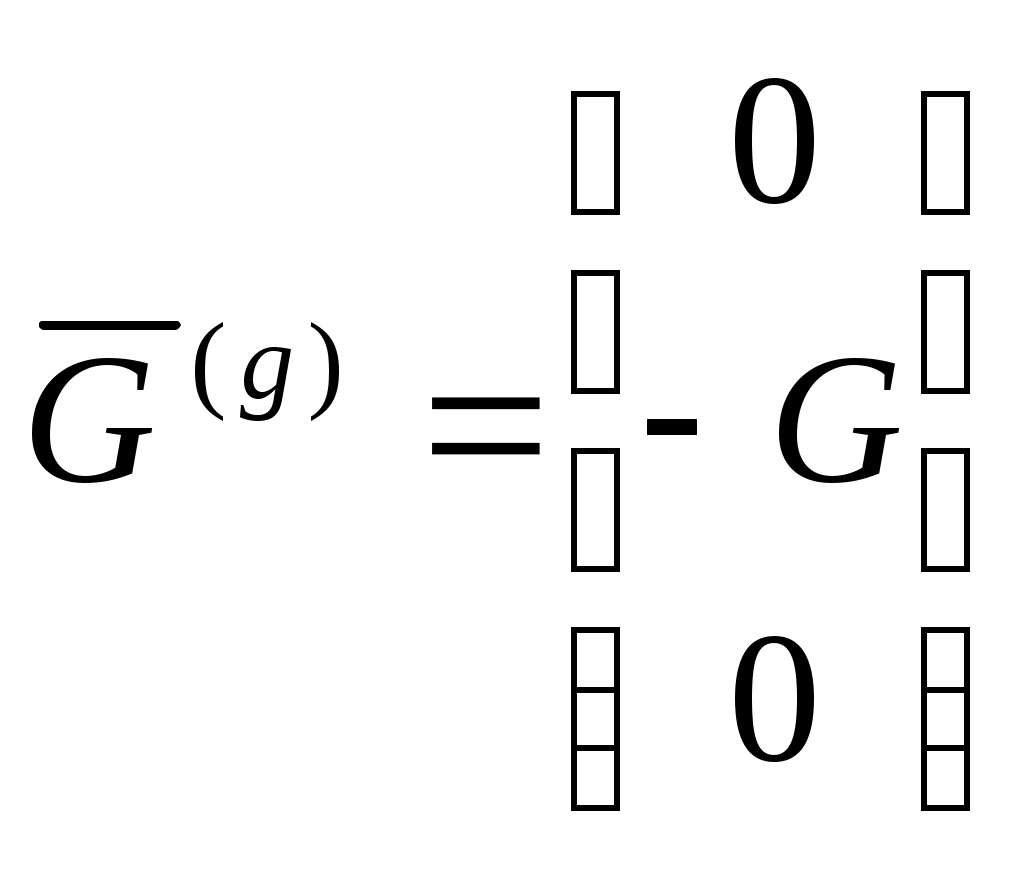 2. Сила тяги двигателя приложена в центре масс двигателя и направлена по оси OX связанной системы. Она задается в базисе связанной системы координат: 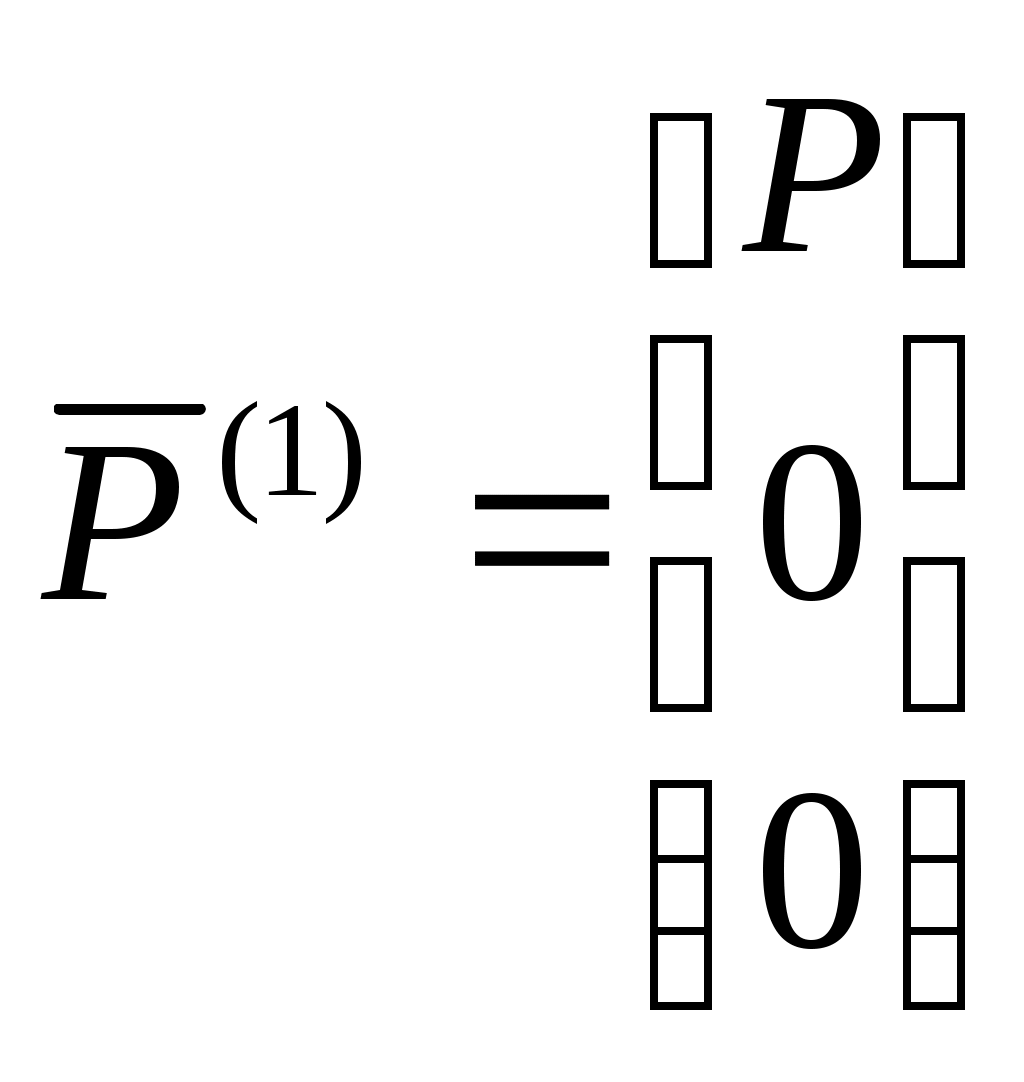 3. Равнодействующая аэродинамических сил обычно записывается в базисе скоростной системы: 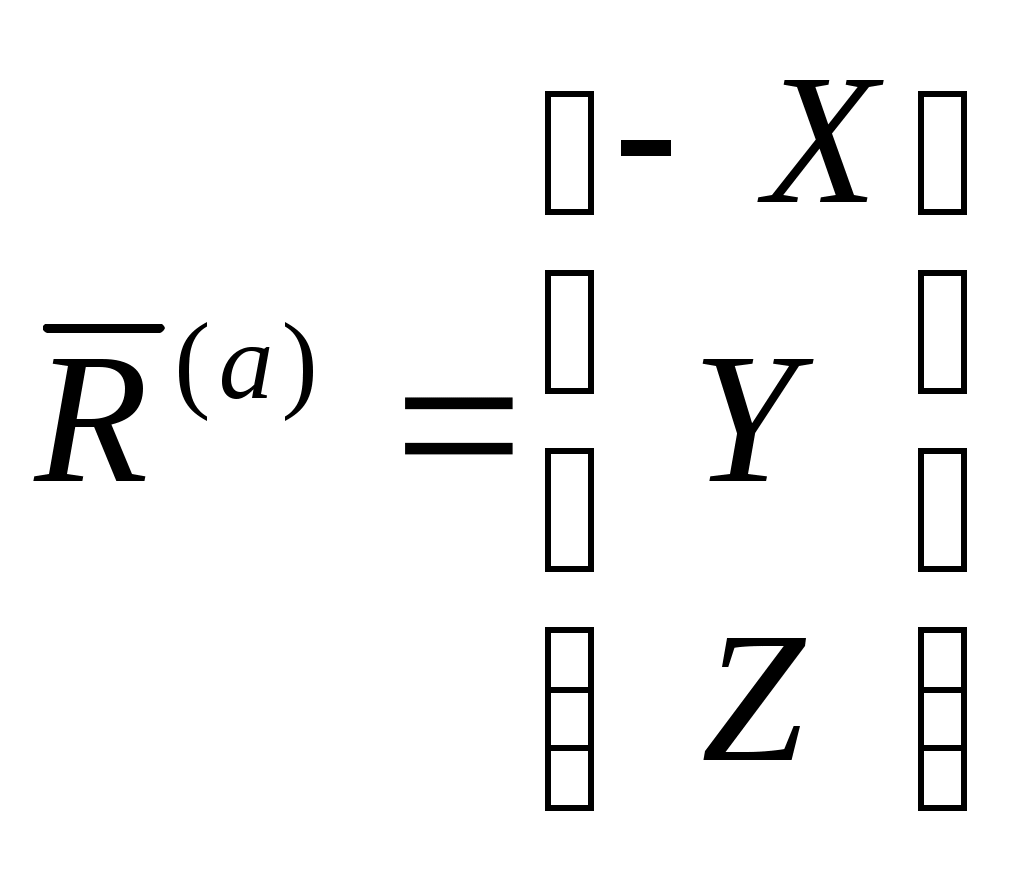 где X – сила лобового сопротивления; Y – подъемная сила; Z – боковая сила. Запишем эти силы в проекциях на оси траекторной системы: 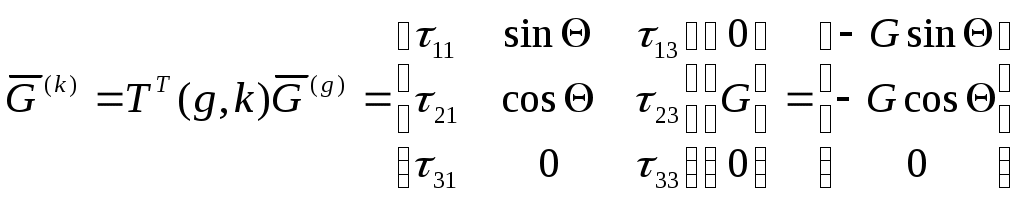 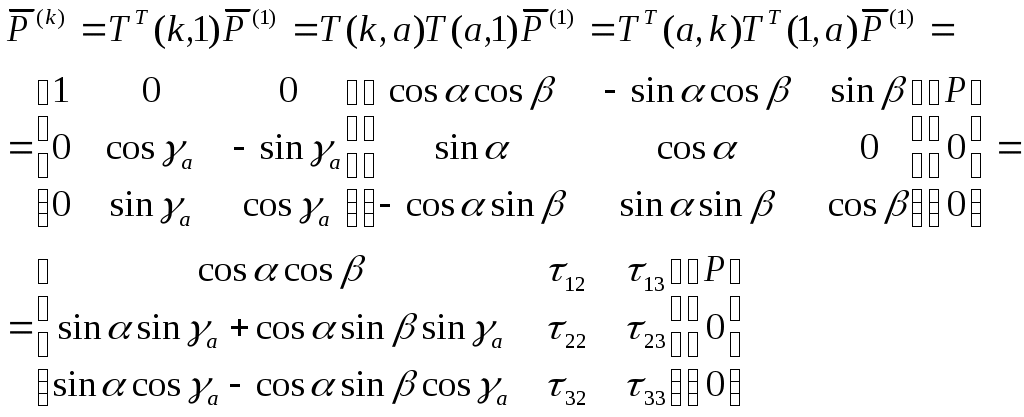 Окончательно 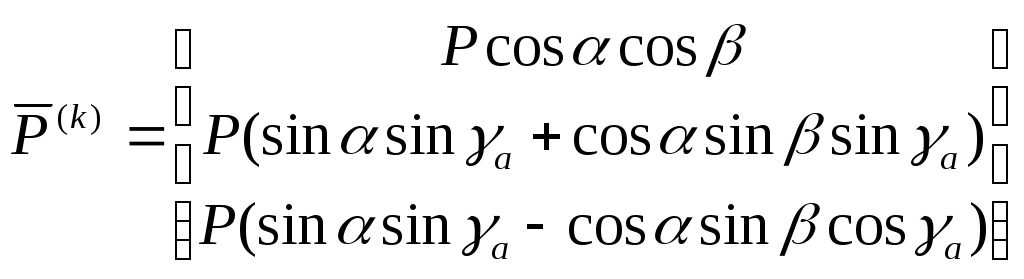 Аэродинамические силы выразятся так: 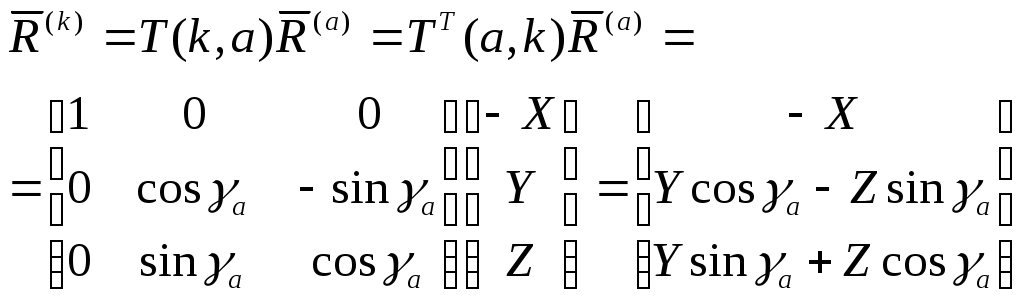 Поскольку проекции вектора скорости в скоростной и траекторной системах координат совпадают, то запишем левую часть уравнения сил в базисе траекторной системы: 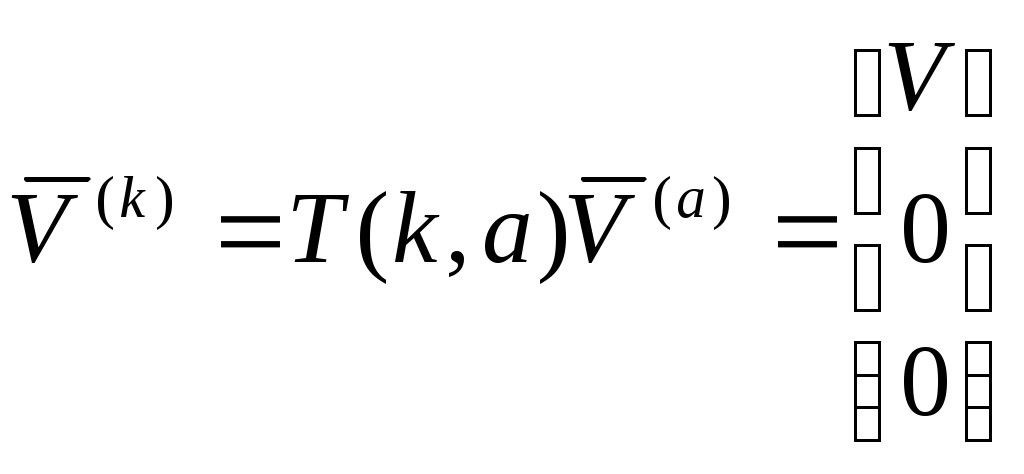 Дифференцируем где 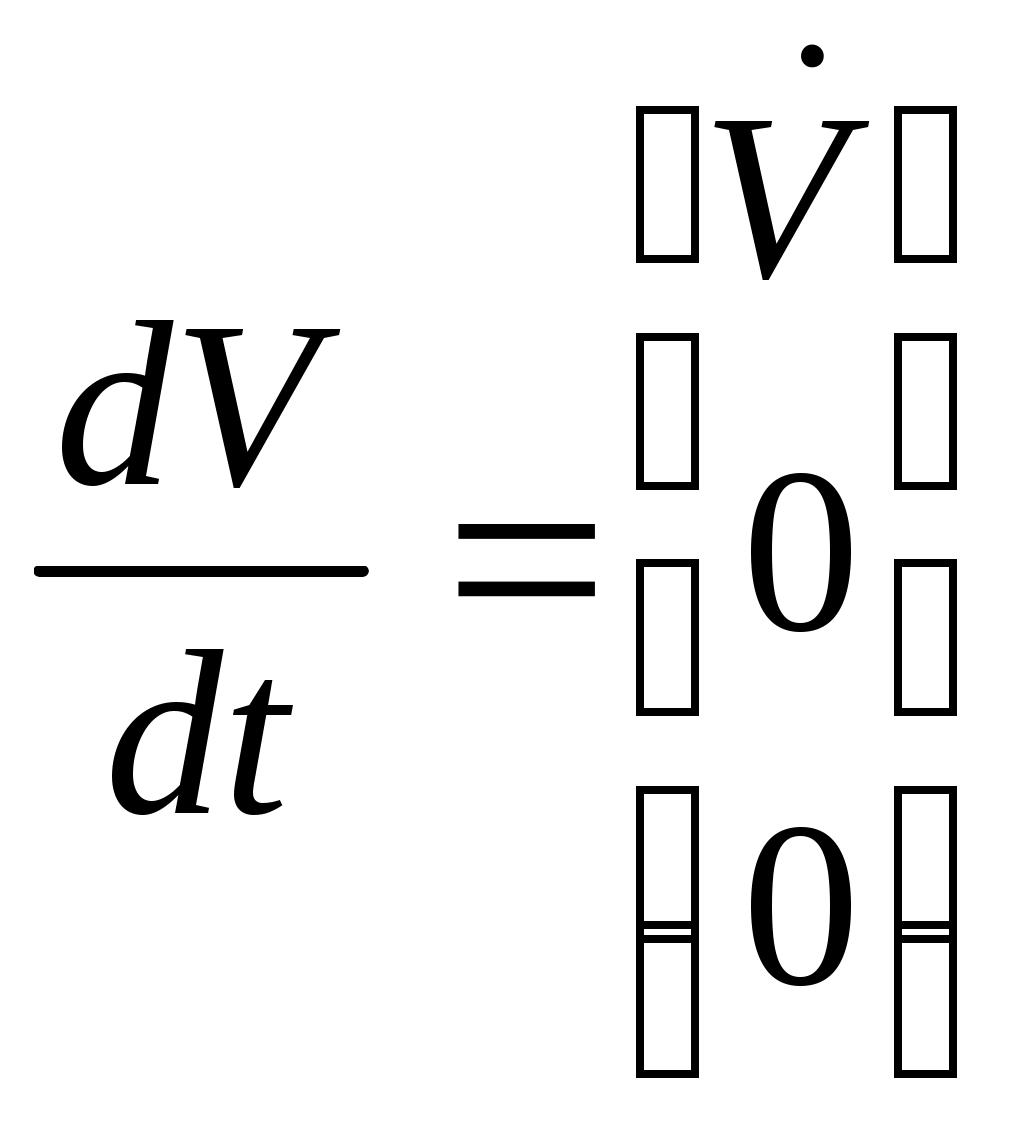 – локальная производная по времени, взятая в предположении неподвижого базиса; – локальная производная по времени, взятая в предположении неподвижого базиса; 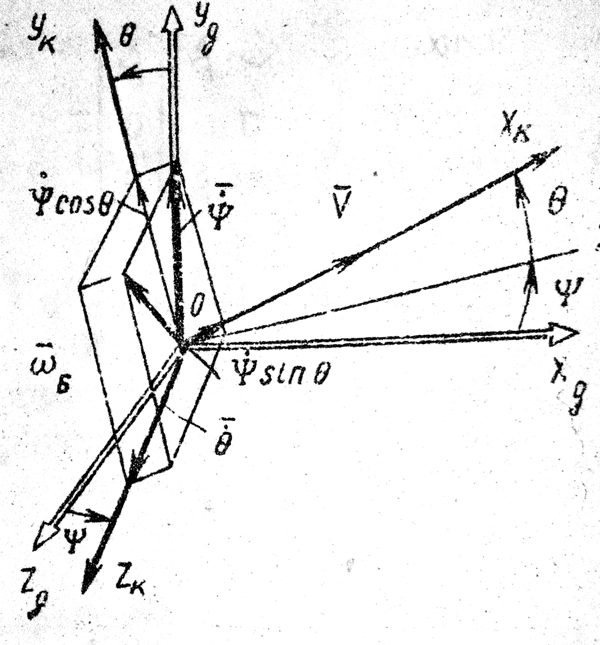 Рис. 8. Вращение базиса траекторной системы координат в нормальной. Обратимся к рис. 8. Нетрудно видеть, что вектор угловой скорости траекторной системы координат 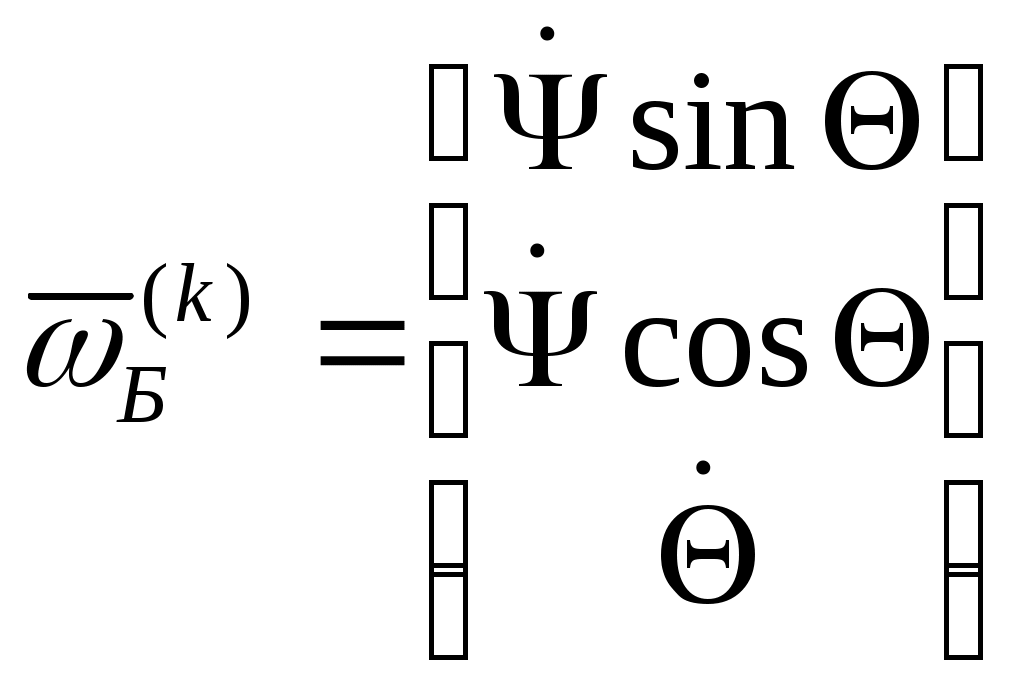 Тогда векторное произведение 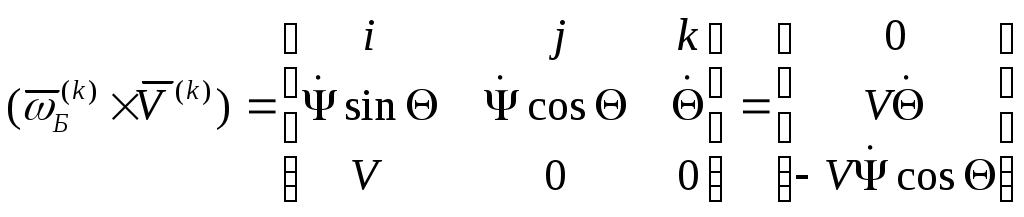 Таким образом, получили уравнения сил в проекциях на оси траекторной системы координат: Уравнение моментов, характеризующее вращение ЛА вокруг центра масс, получим на основании теоремы об изменении кинетического момента: где Здесь 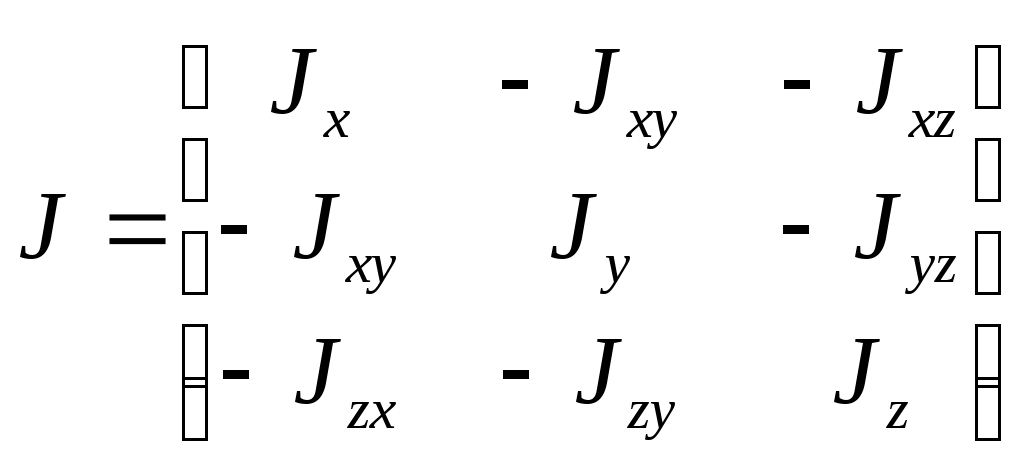 – тензор инерции (здесь главными являются оси связанной системы координат); – тензор инерции (здесь главными являются оси связанной системы координат);Для ЛА, имеющих две взаимно перпендикулярные плоскости симметрии, 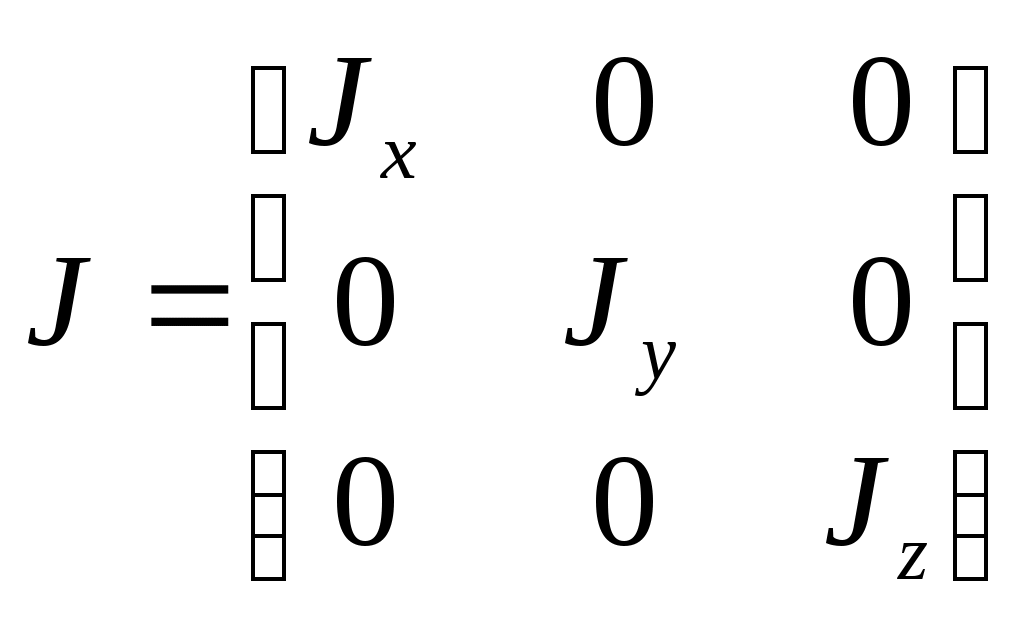 . .Для самолетов 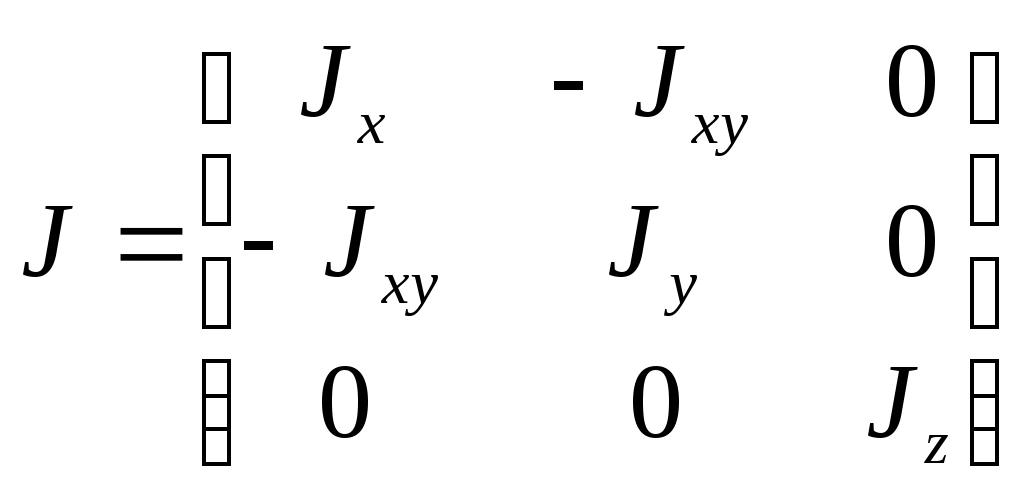 . .Уравнение моментов в аэродинамике проецируют на оси связанной системы координат. Положим, что ЛА имеет две плоскости симметрии, т.е. 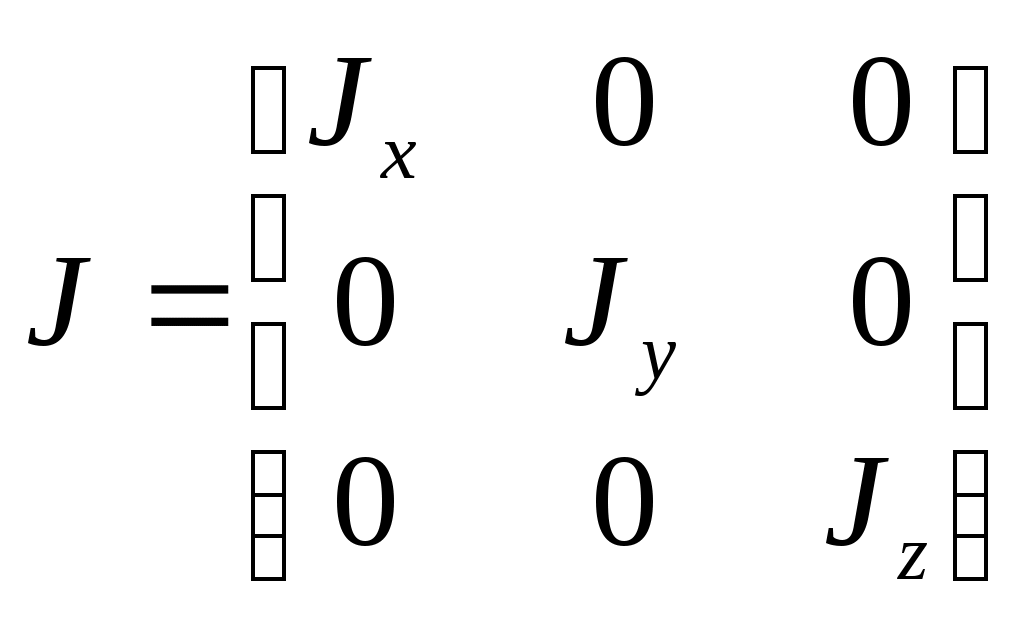 . .Запишем вектор угловой скорости в проекциях на оси связанной системы: 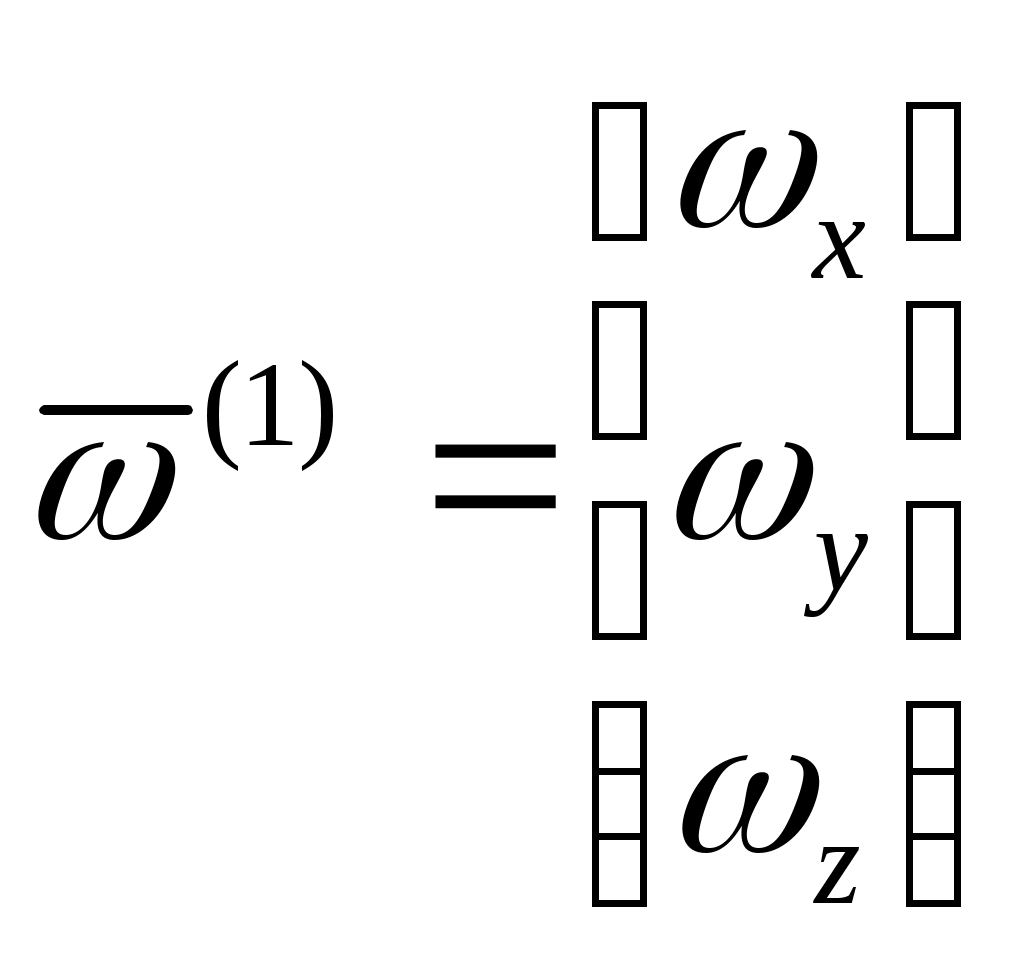 . .Тогда 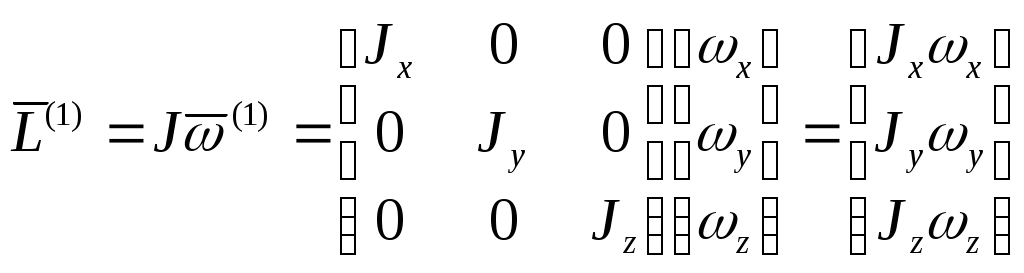 Найдём полную производную 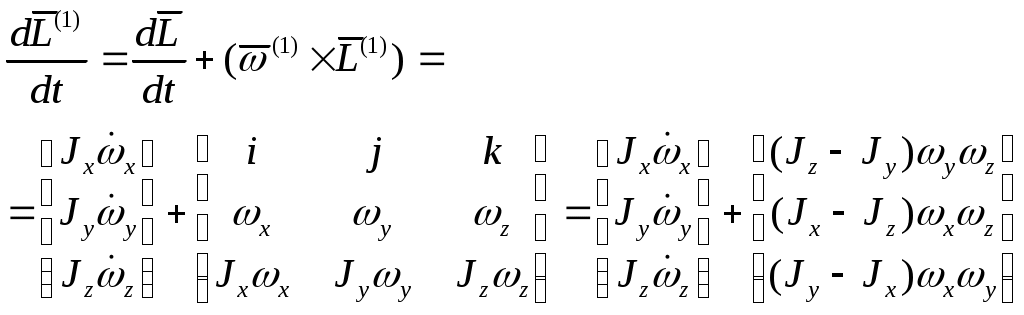 Внешние моменты, действующие на ЛА в проекциях на связанные оси, запишем в следующем виде: 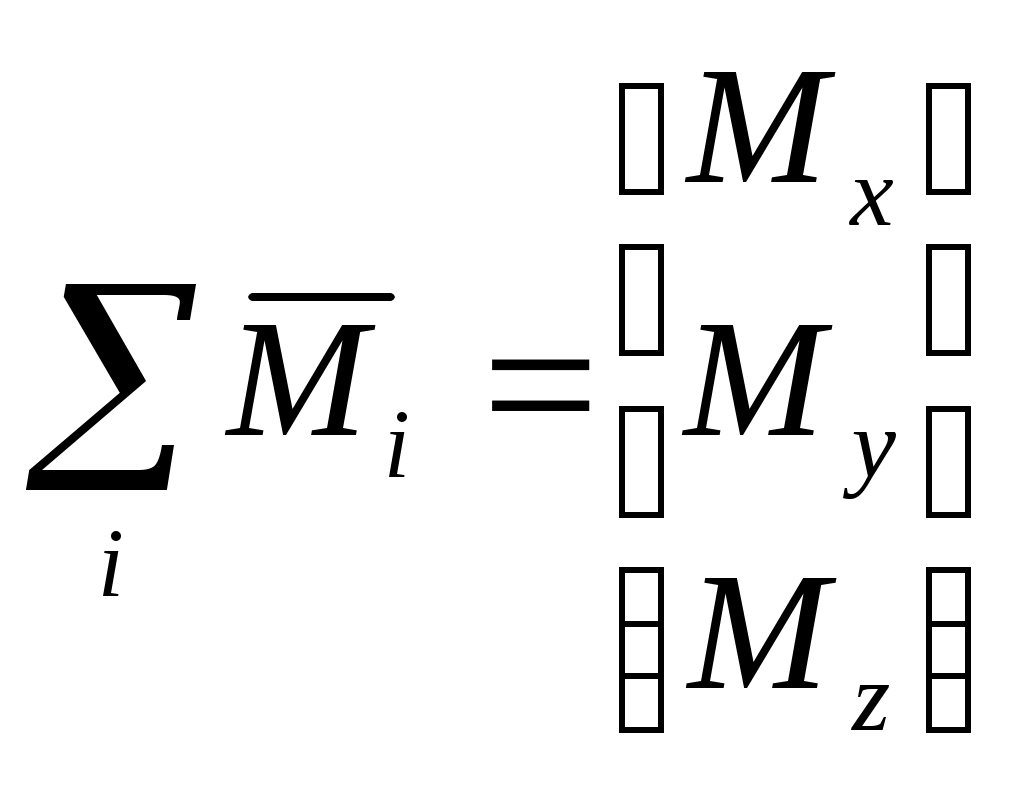 Таким образом, имеем: Для ЛА с двумя плоскостями симметрии, как правило, выполняется соотношение Теперь необходимо составить кинематические уравнения, характеризующие вращения ЛА относительно осей нормальной системы координат. В уравнениях (4) – (6) заданы проекции угловой скорости относительно связанных осей: 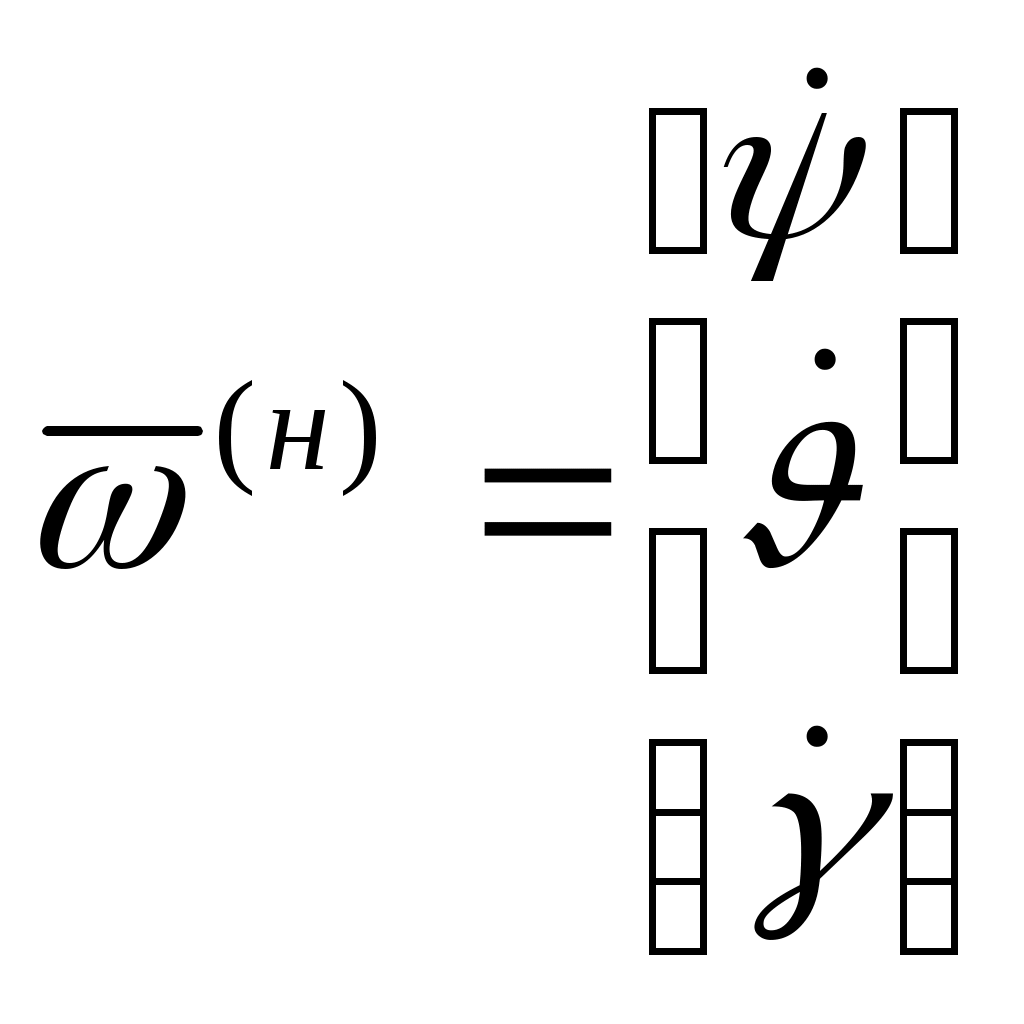 Из рис. 5 видно, что Отсюда запишем матрицу перехода от непрямоугольной системы к связанной: 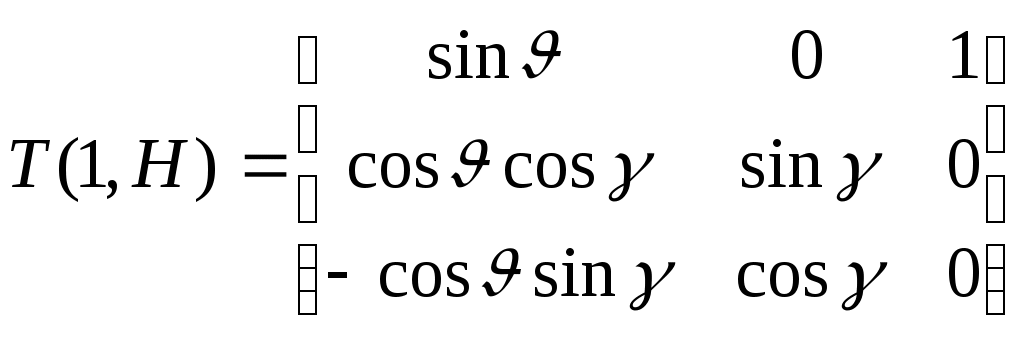 Обычно требуется провести обратное преобразование T(H,1), которое находят по обычным правилам вычисления обратных матриц: Нетрудно видеть, что определитель Запишем взаимную матрицу 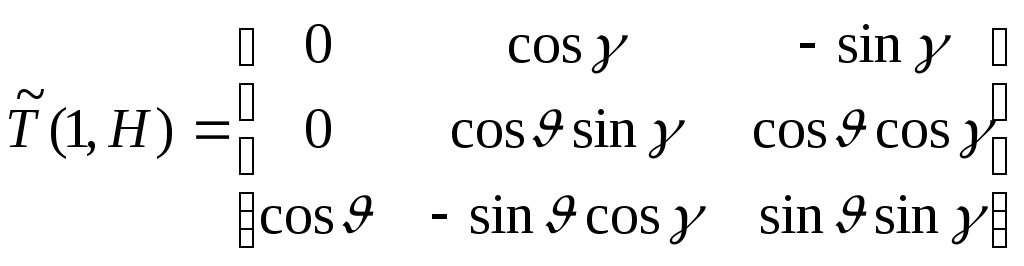 . .Таким образом, связь между проекциями угловой скорости в разных базисах выражается следующими уравнениями: Поскольку уравнения движения центра масс (1), (2), (3) записаны в траекторных осях, уравнения вращательного движения вокруг центра масс (4) – (9) – в связанных осях, а аэродинамические силы и моменты в правых частях уравнений (1) – (6) зависят от углов атаки Матрица T(a,g) нами получена выше. Найдем 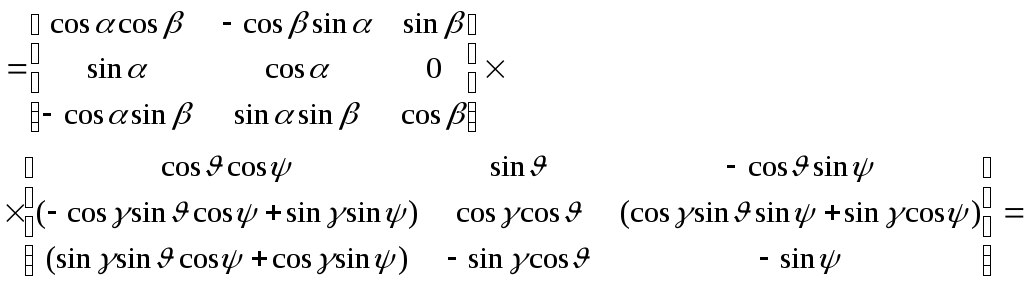  В силу свойств ортогональных матриц, связывающих их элементы равенствами, остаются независимыми три равенства, составляемые из элементов матриц Дополним эту систему уравнениями, задающими проекции линейной скорости ЛА в нормальных осях координат. Используем при этом матрицу перехода от нормальной к траекторной системе: 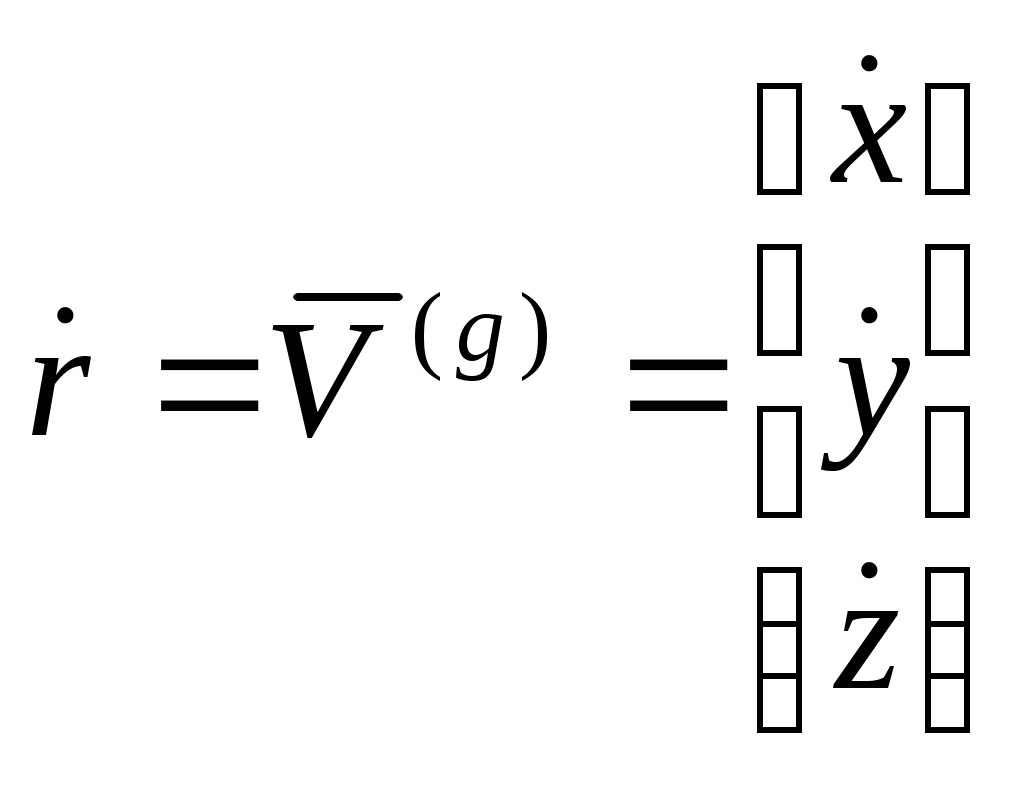 ; ; 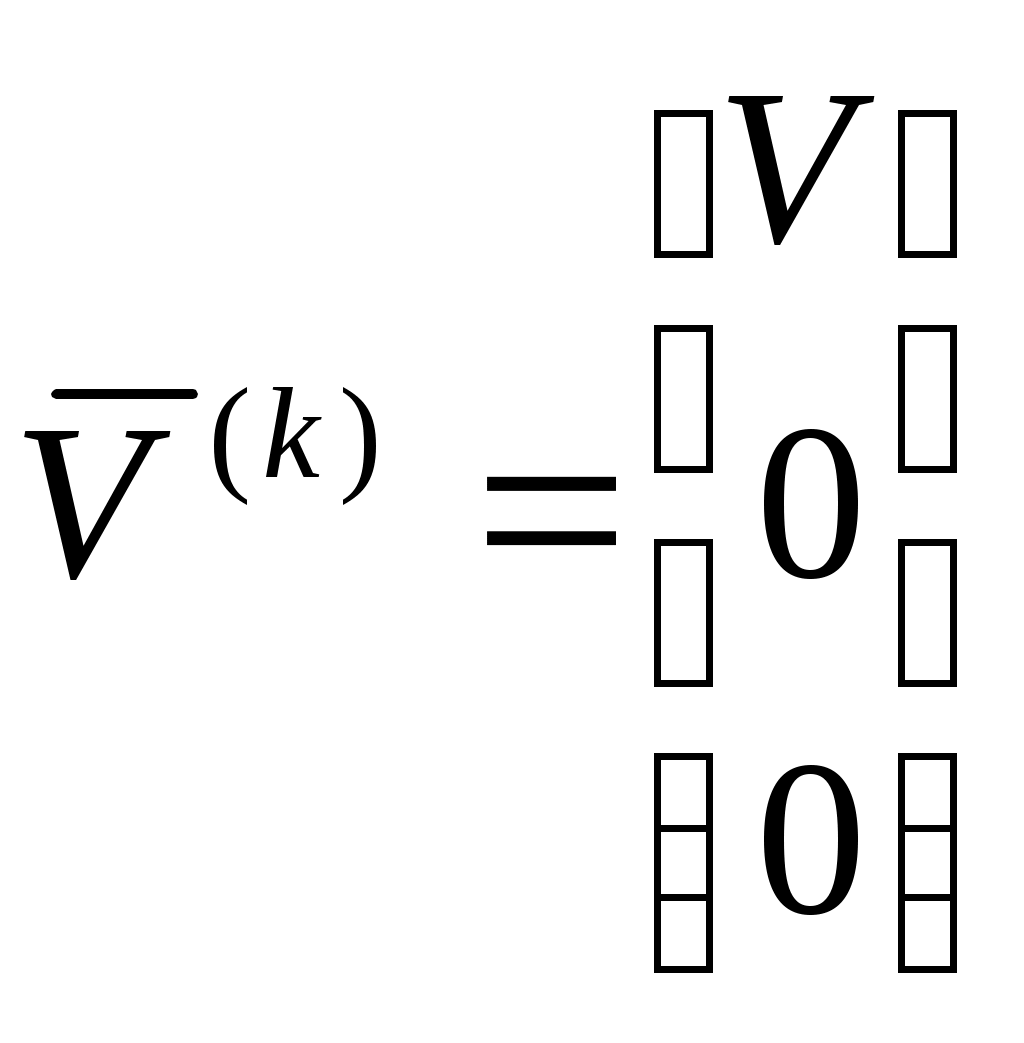 ; ; 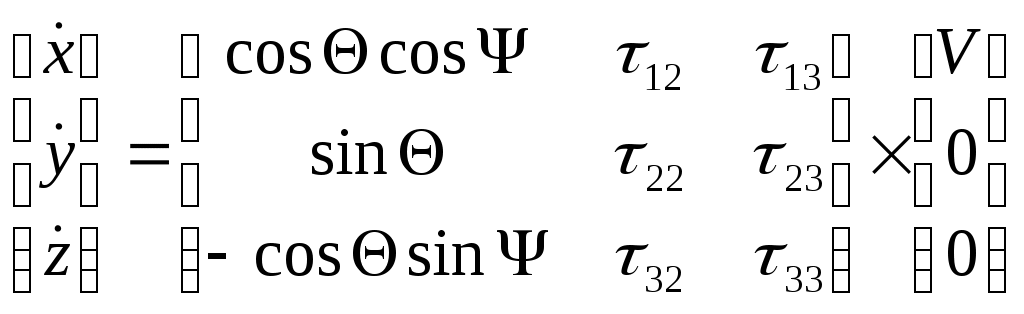 Итак, уравнения движения центра масс в нормальных осях выразятся так: Дадим последнее уравнение – уравнение тяги двигателя: Поскольку Земля имеет сферическую форму, необходимо задать функцию высоты от текущих координат ЛА в нормальной системе координат H=H(x,y,z). Если сферичностью пренебречь, что допустимо для траекторий движения ЛА широкого класса, то можно считать, что Из аэродинамики известно [5], что аэродинамические силы и моменты, входящие в уравнения (1) – (6), могут быть вычислены по формулам: 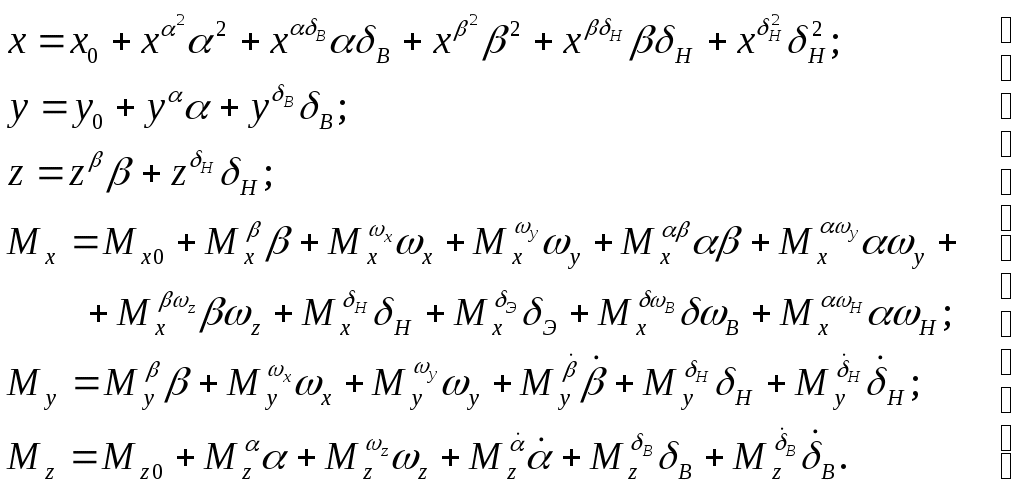 (17) (17)Здесь x0 – значение x при y0 – значение y при Mx0 – значение Mx при Mx0 – значение Mx при Полученная система уравнений (1) – (16) содержит 13 дифференциальных уравнений первого порядка и три геометрических соотношения. В случае неуправляемого полета или полета с зафиксированными органами управления данная система является замкнутой, т. е. число неизвестных переменных В случае управляемого полета данная система уравнений не является замкнутой, так как проекции аэродинамических сил и моментов в правых частях уравнений будут зависеть от углов отклонения органов управления: Если задать отклонения органов управления как известные функции времени, то при заданных начальных условиях и номинальных значениях параметров аппарата будет определена единственная траектория движения ЛА, которую назовем траекторией невозмущенного движения. На самом деле в реальном полете отклонение органов управления осуществляется от программного устройства через автопилот. И вообще бортовая система управления должна обеспечивать вполне определенную функциональную связь между отклонениями органов управления и текущими значениями параметров полета: 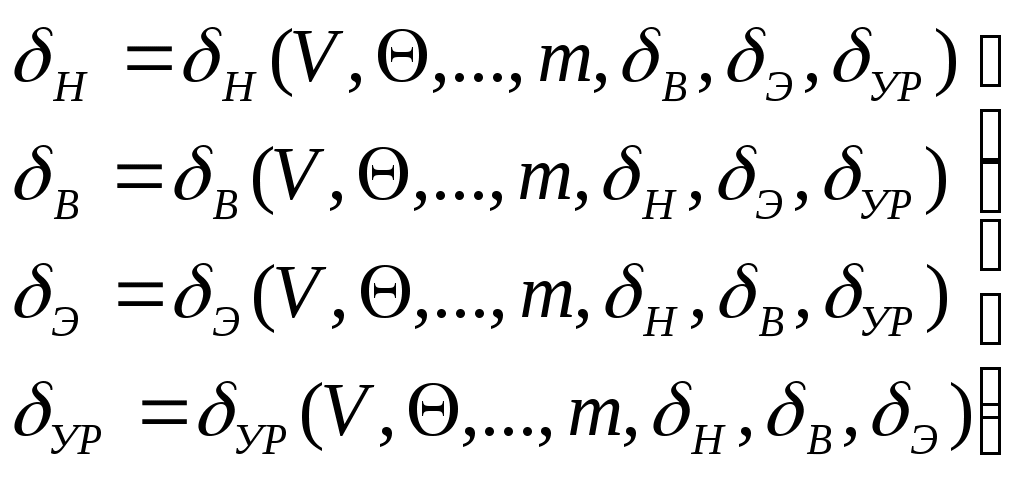 (18) (18)С учётом этого требования система уравнений (1) – (16), (18) становится замкнутой и для управляемого полета. В действительном полете начальные условия всегда отличаются от заданных, на ЛА действуют в случае аэродинамические силы, связанные с турбулентностью атмосферы, система управления отрабатывает требуемую функциональную связь (18) параметров полета, с некоторыми, вообще говоря, случайными ошибками. Поэтому параметры полета всегда отличаются от их теоретического значения, а реальную траекторию называют траекторией возбужденного движения. 1 2 |
