Решебник. Свойства определителей
 Скачать 86 Kb. Скачать 86 Kb.
|
|
§ 4. Свойства определителей Свойство 1. Величина определителя не изменится, если все его строки заменить столбцами, причём каждую строку заменить столбцом с тем же номером, т. е. 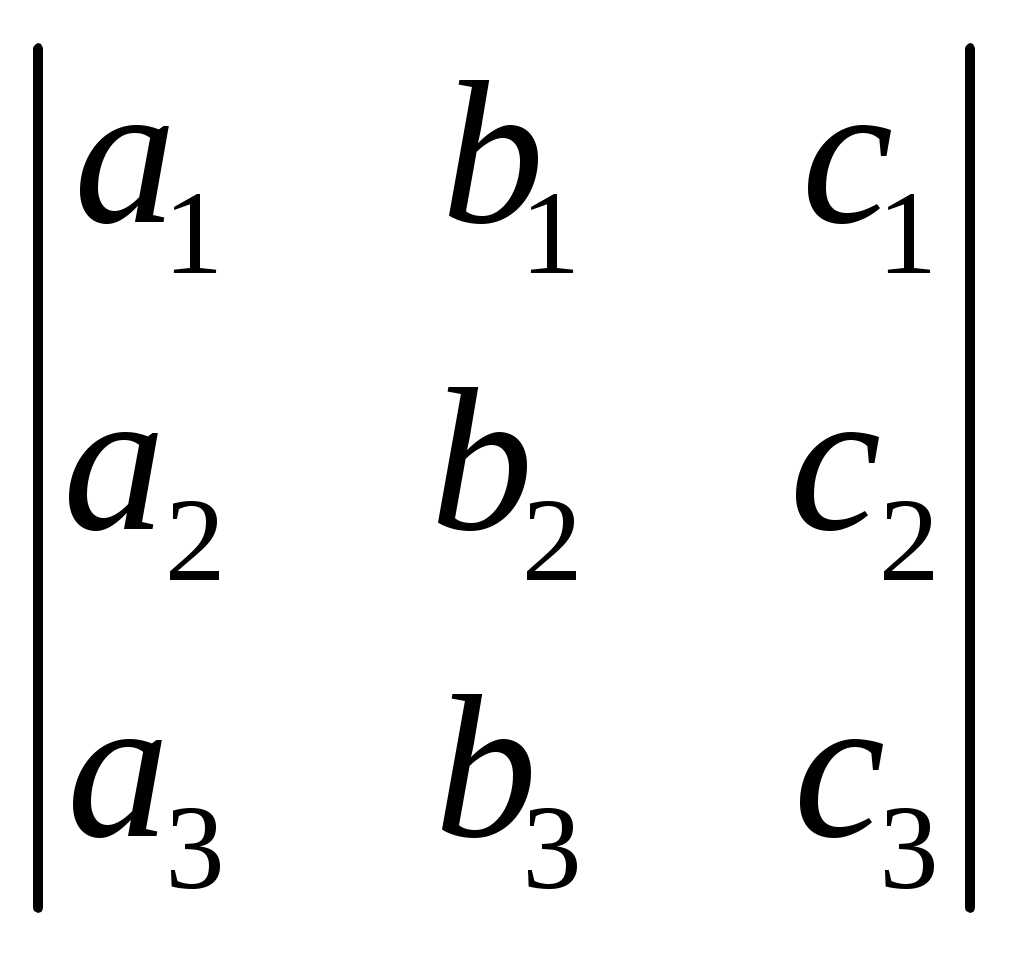 = = 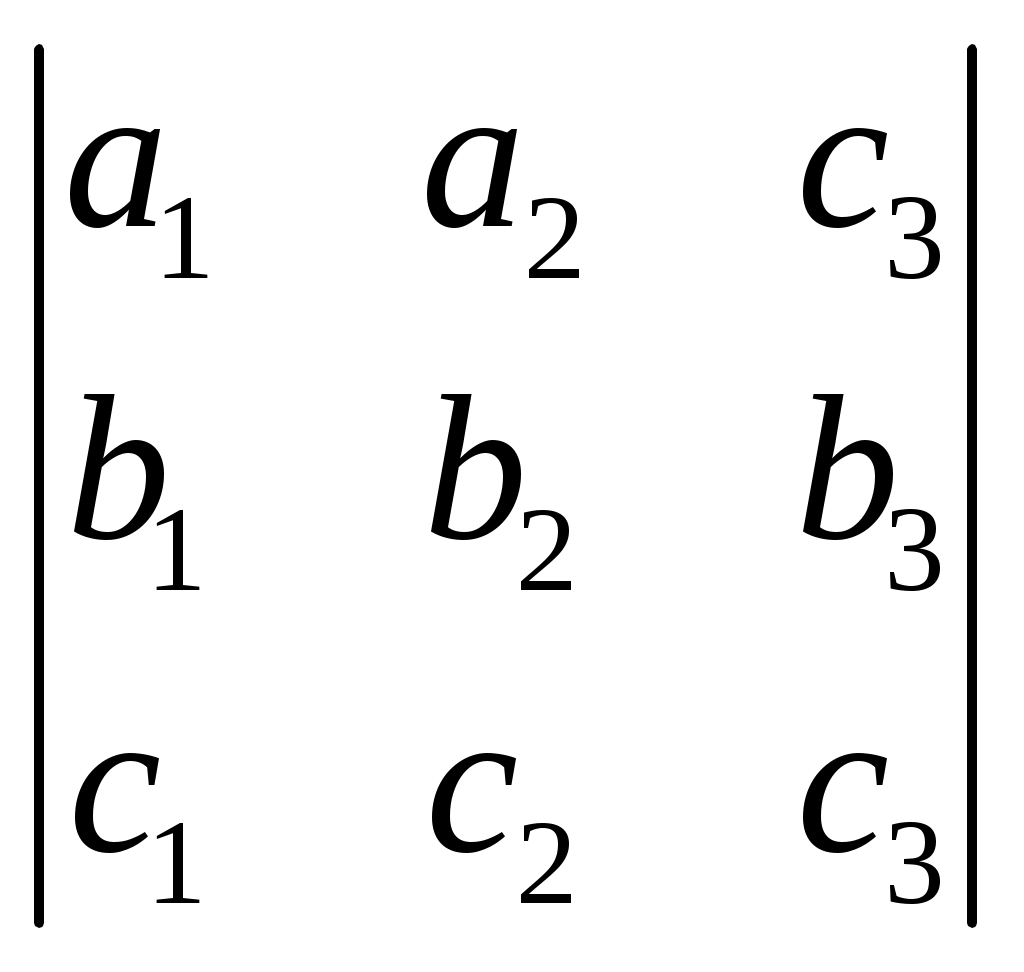 . .Свойство 2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на — 1. Например, 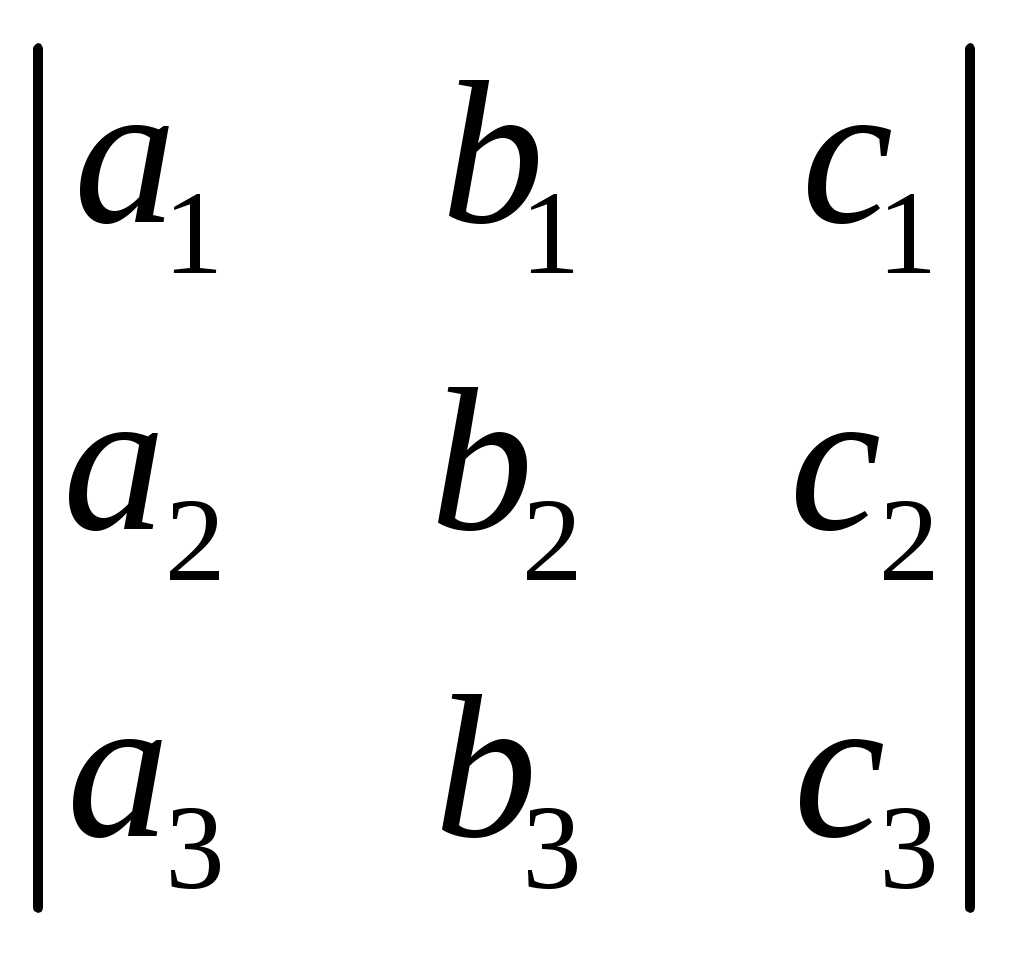 = — = —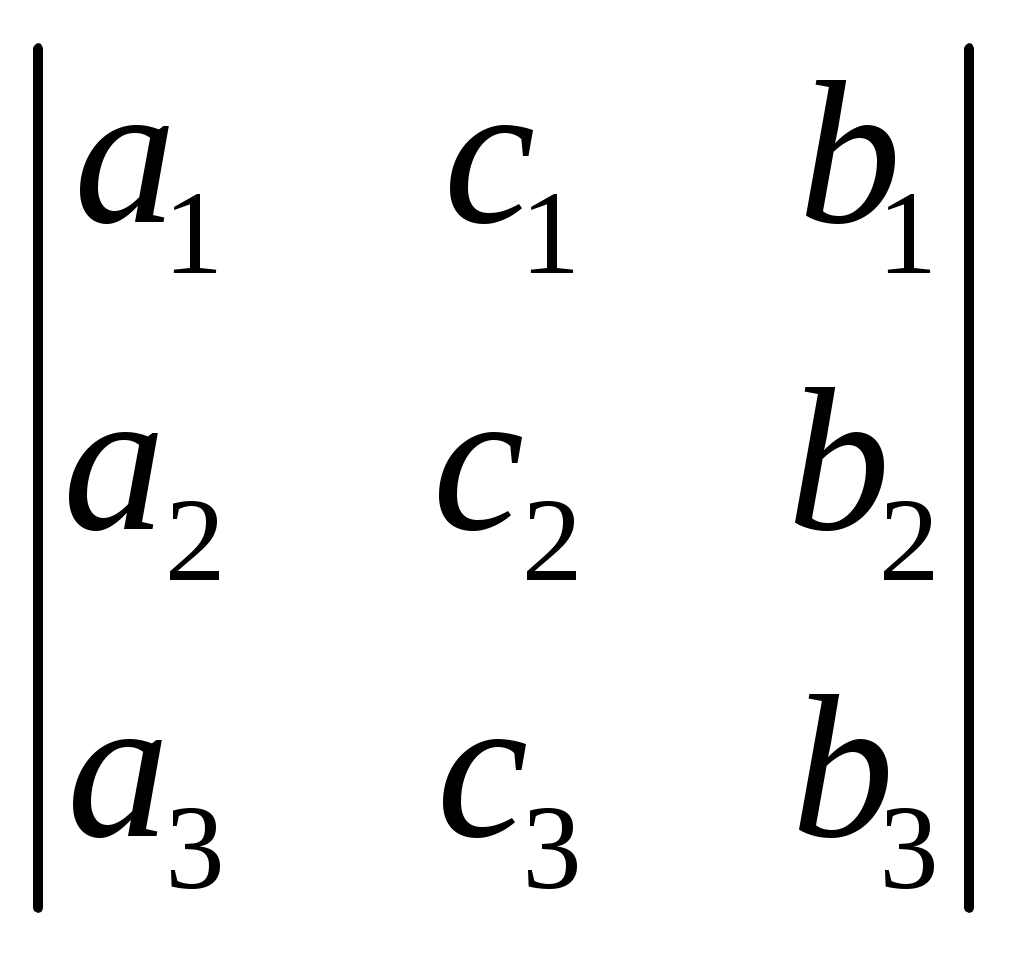 . .Свойство 3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю. Свойство 4. Умножение всех элементов одного столбца или одной строки определителя на любое число kравносильно умножению определителя на это число k. Например, 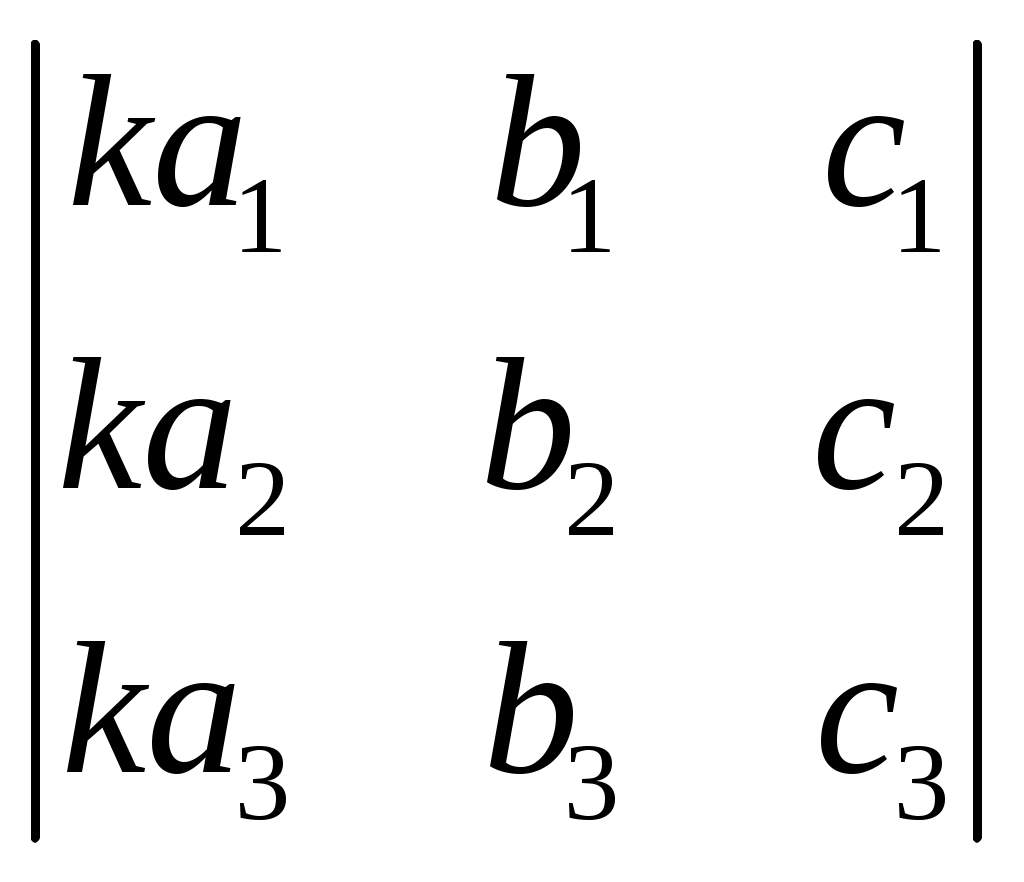 = k = k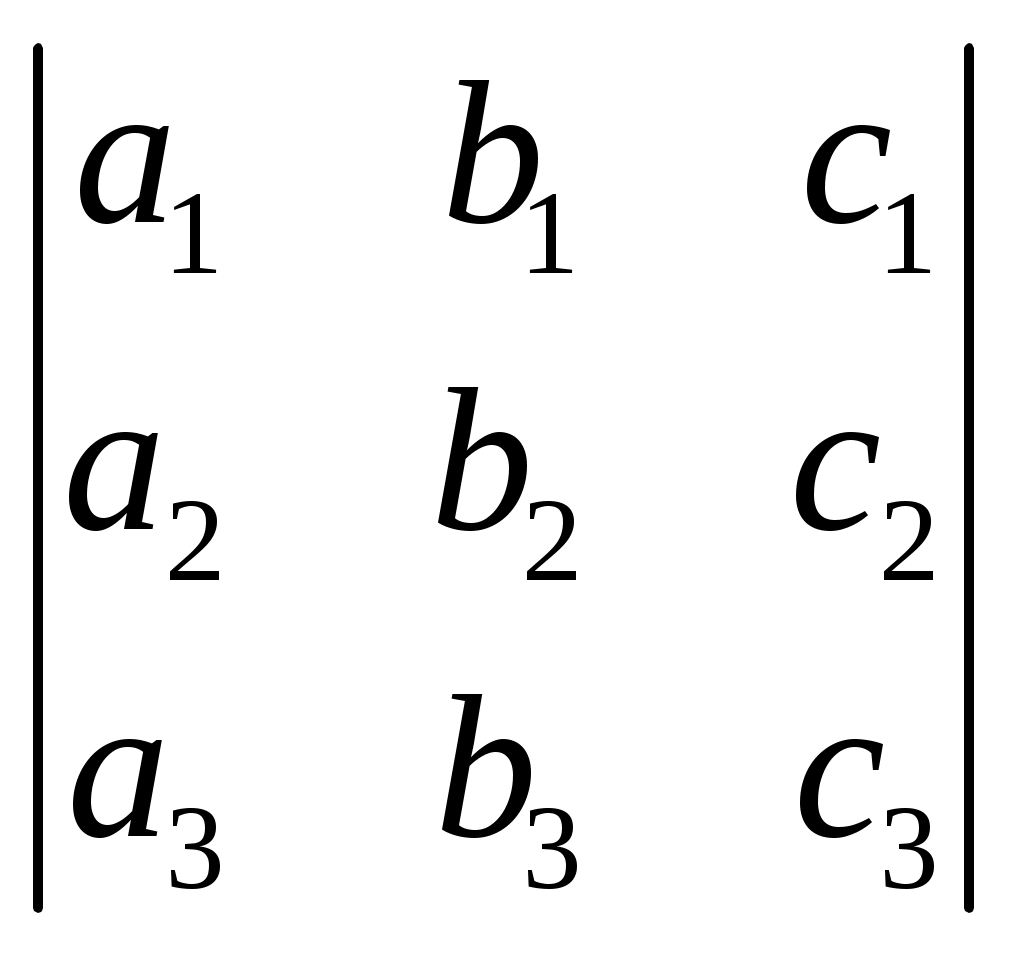 . .Свойство 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случай предыдущего (при k = 0). Свойство 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю. Свойство 7. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце, или соответственно в n-й строке, имеет первые из упомянутых cлагаемых, а другой — вторые; элементы, стоящие на остальных местах, у всех трёх определителей одни и те же. Например, 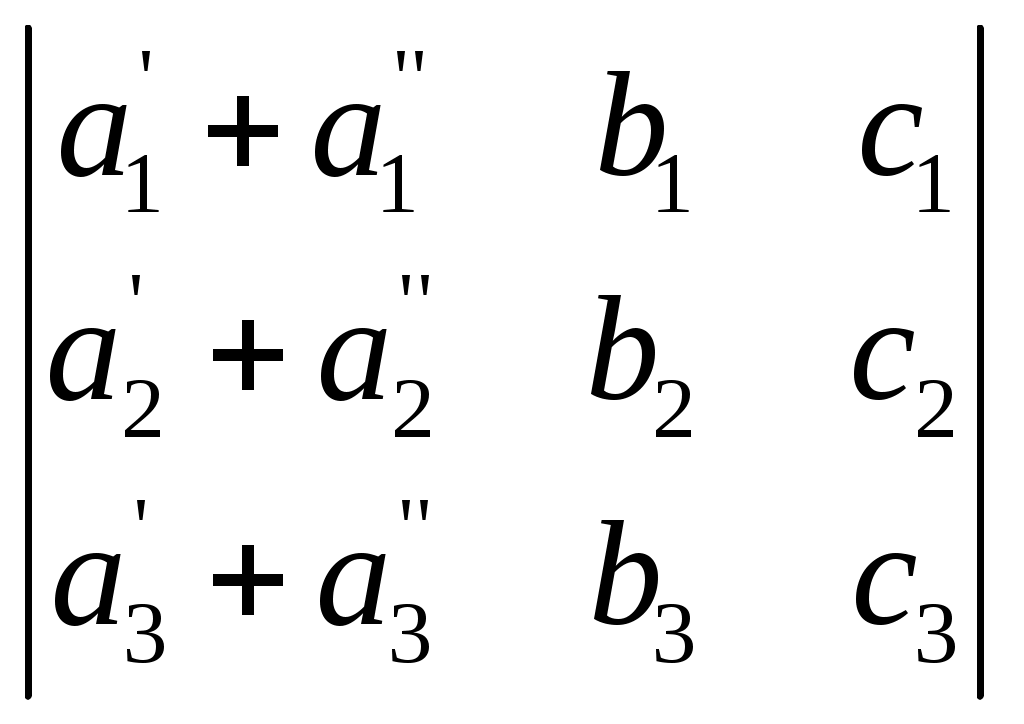 = = 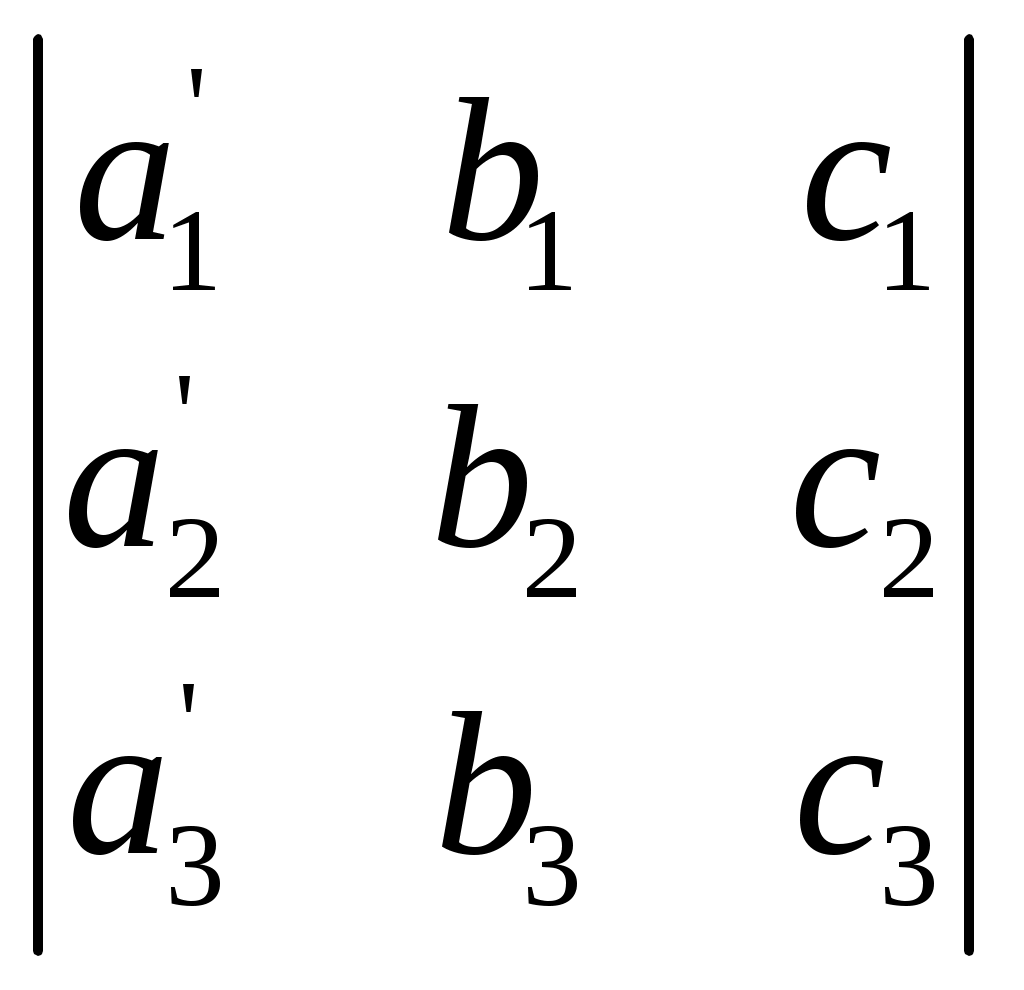 .+ .+ 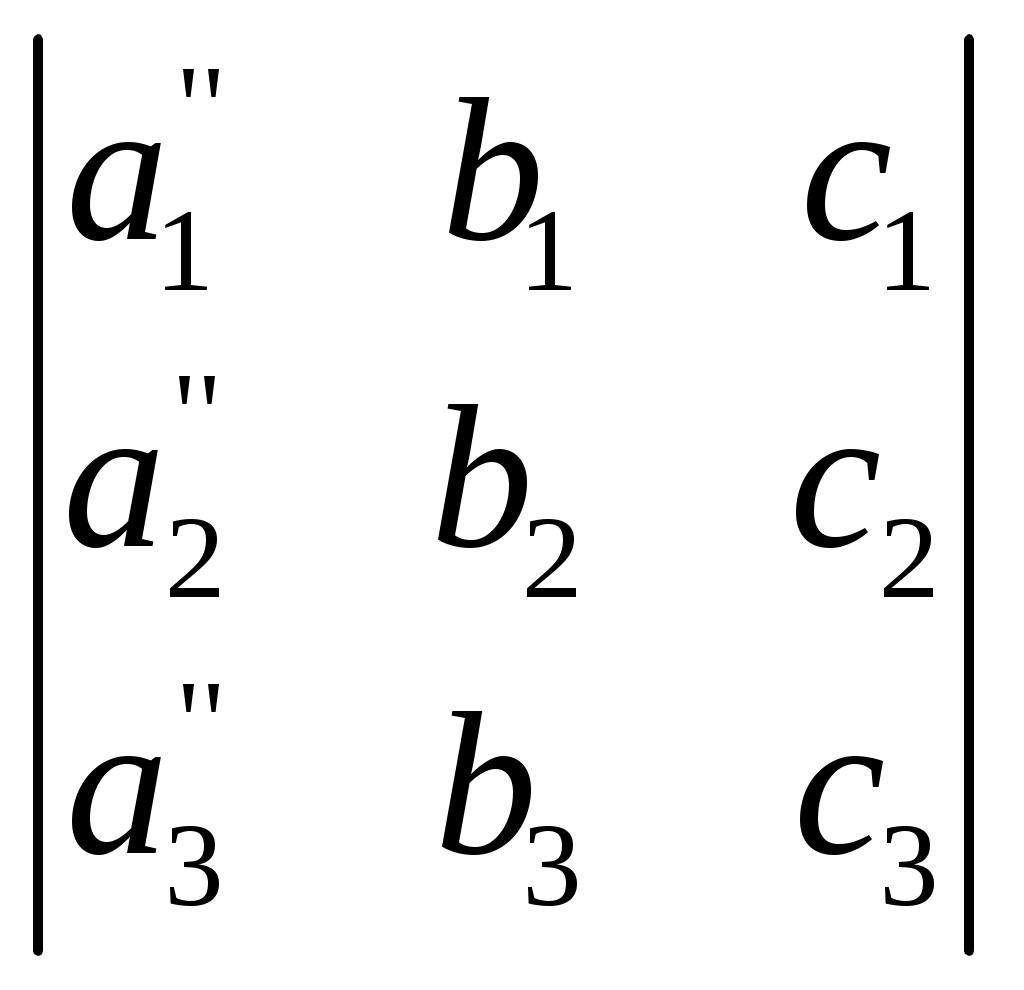 Свойство 8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится. Например, 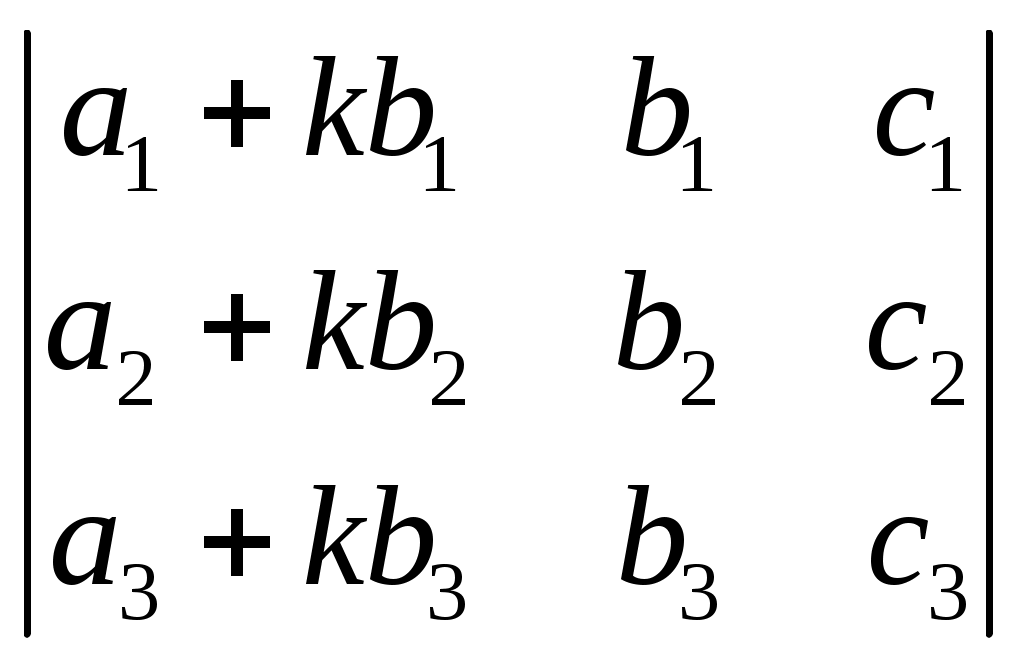 = = 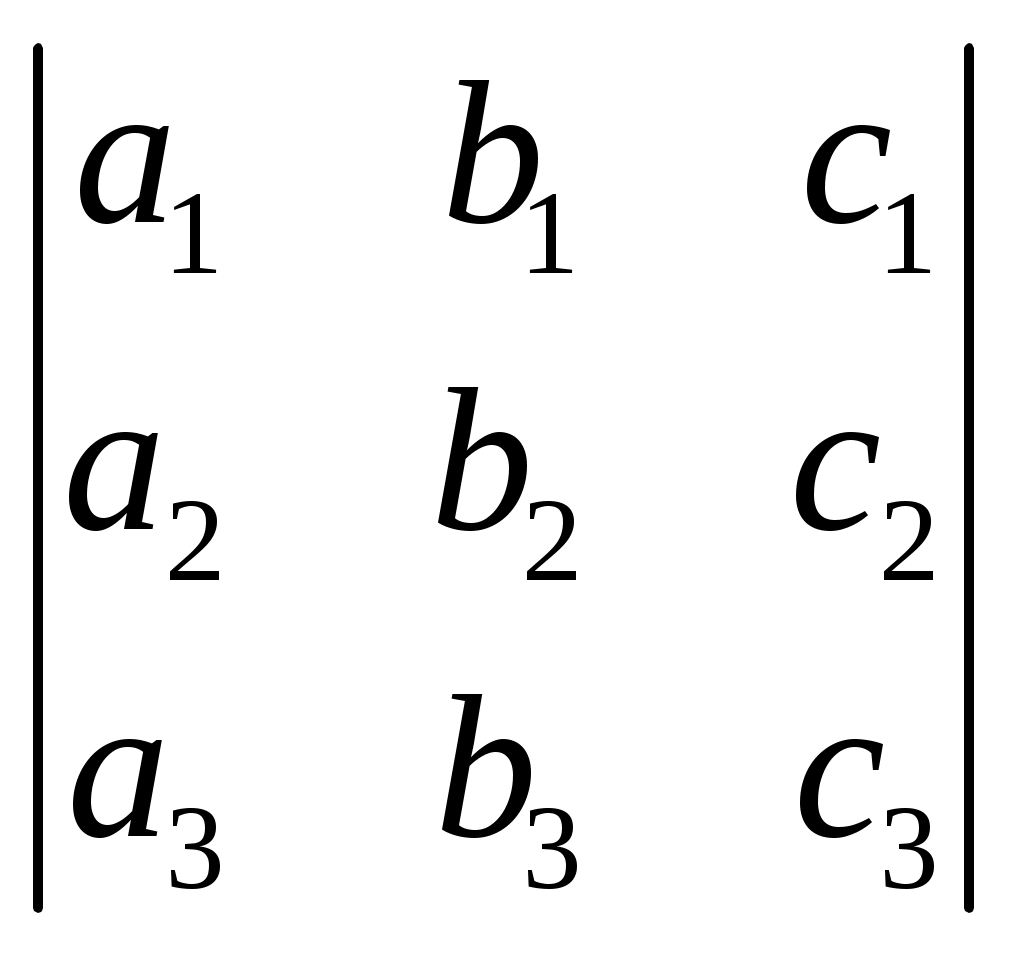 . .Дальнейшие свойства определителей связаны с понятием алгебраического дополнения и минора. Минором некоторого элемента называется определитель, получаемый из данного путём вычёркивания строки и столбца, на пересечении которых расположен этот элемент. Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число чётное, и с обратным знаком, если это число нечётное. Алгебраическое дополнение элемента мы будем обозначать большой буквой того же наименования и тем же номером, что и буква, которой обозначен сам элемент. Свойство 9. Определитель = 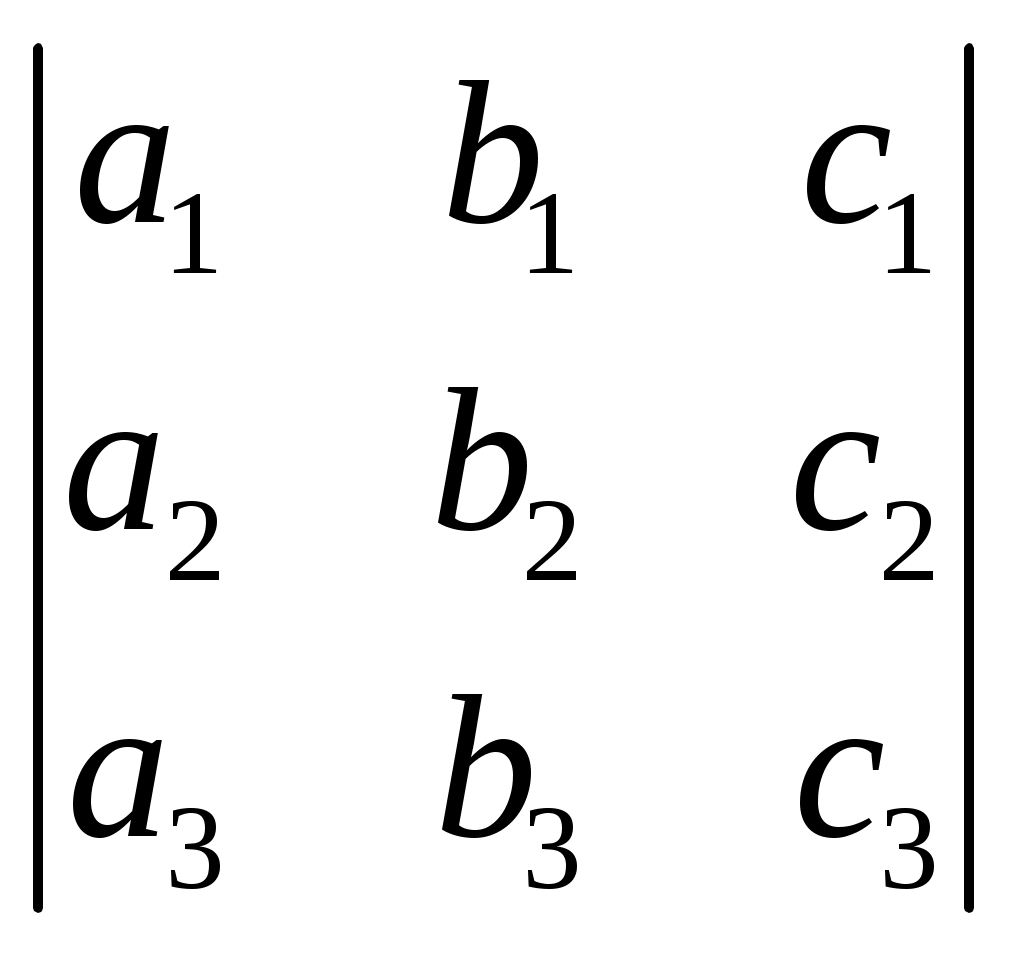 равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения. Иначе говоря, имеют место следующие равенства: = a1A1 + a2A2 + a3A3, = a1A1 + b1B1 + c1C1, = b1B1 + b2B2 + b2B2, = a2A2 + b2B2 + c2C2, = c1C1 + c2C2 + c3C3, = a3A3 + b2B2 + c3C3. В задачах 1217—1222 требуется, не раскрывая определителей, доказать справедливость равенств. 1217. 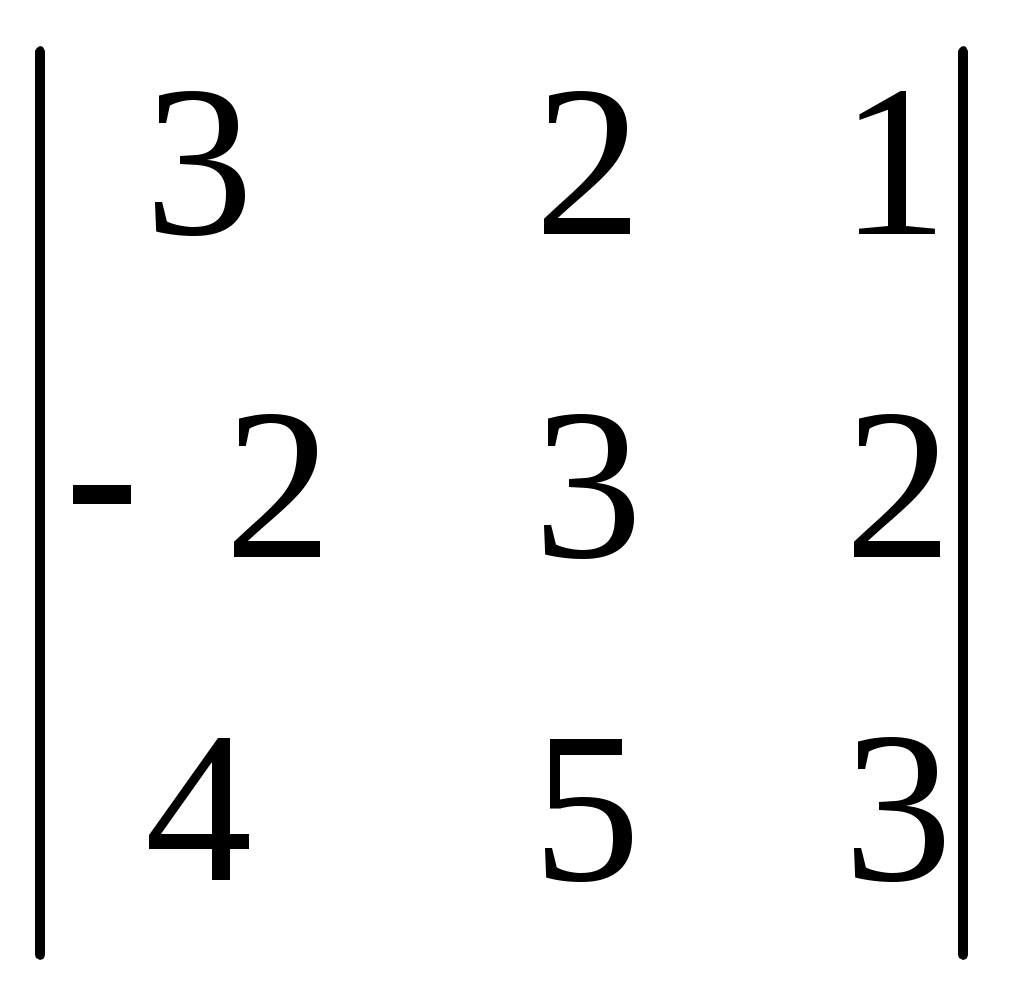 = = . .Указание, Воспользоваться свойством 8. 1218.  = =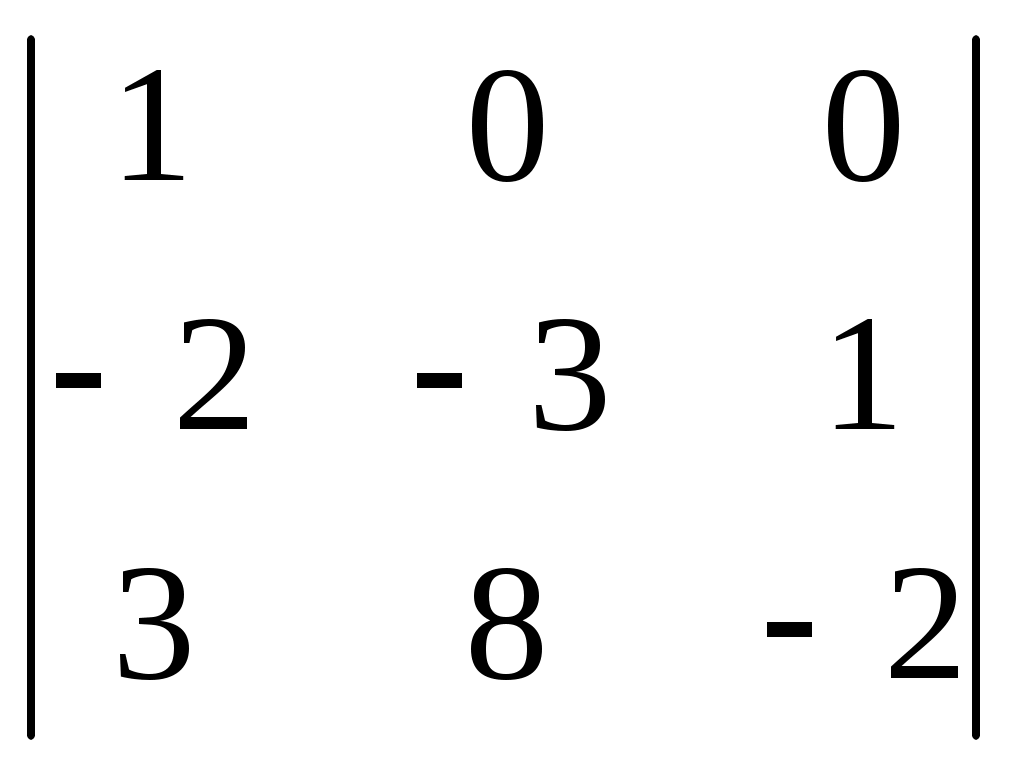 . .У к а з а н и е. Воспользоваться свойством 8. 1219. 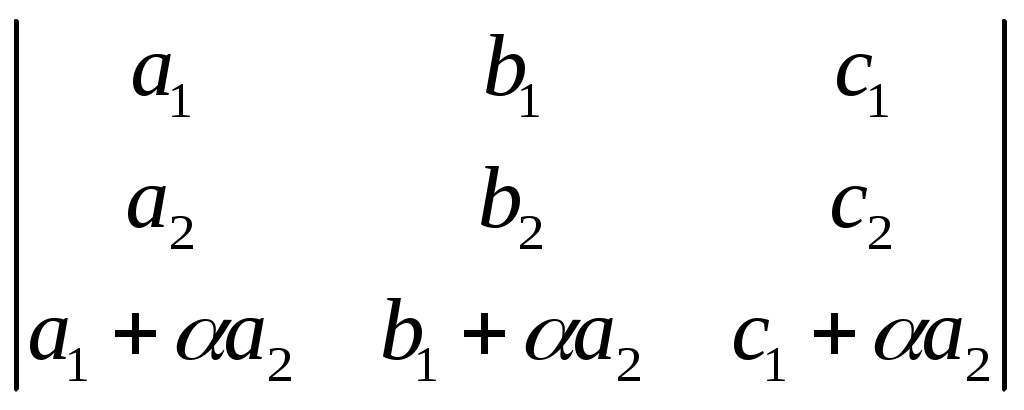 =0 =0Указание. Воспользоваться свойствами 7, 3, 6. 1220. 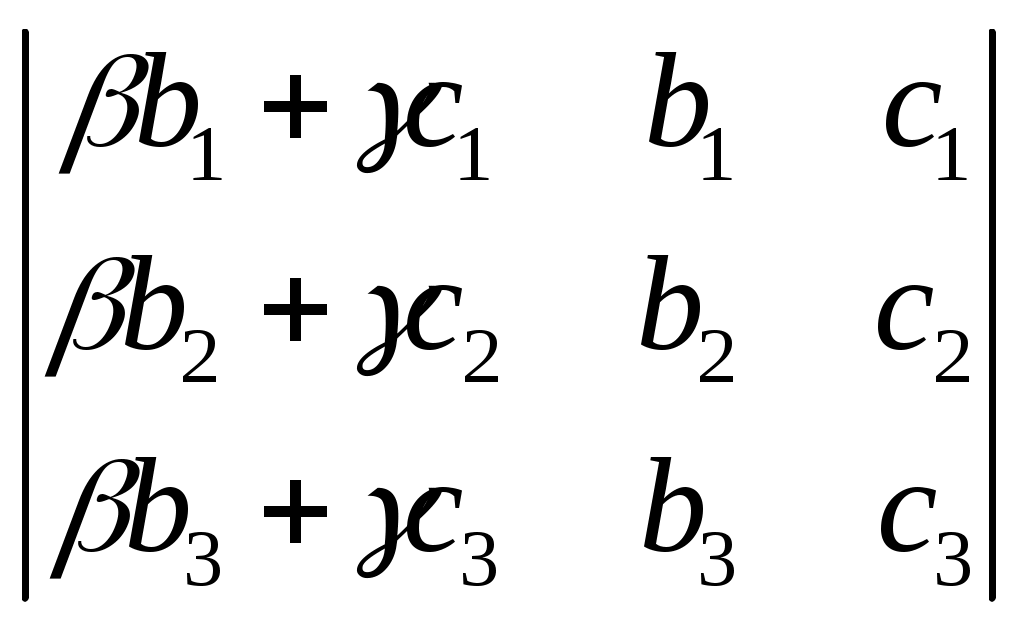 =0 =0У к а з а н и е. Воспользоваться свойствами 7 и 6. 1221. 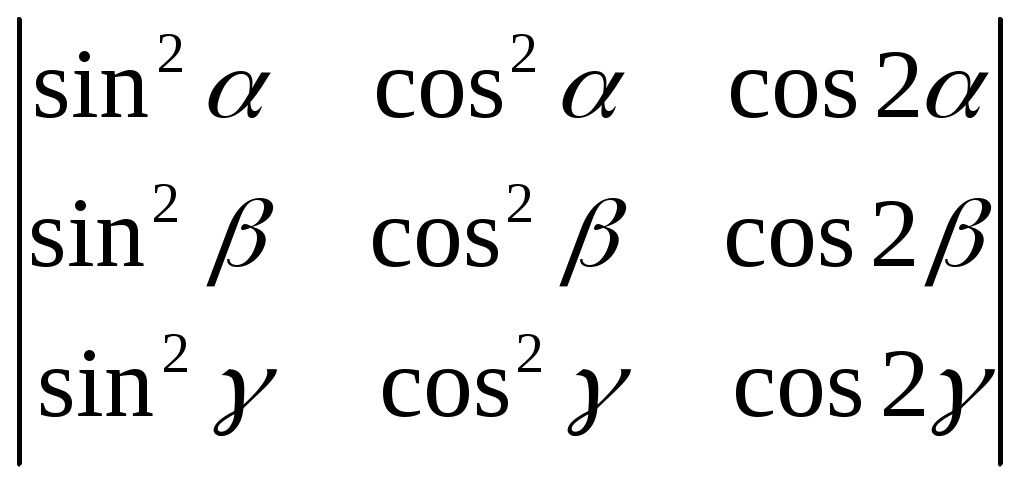 =0 1222. =0 1222. 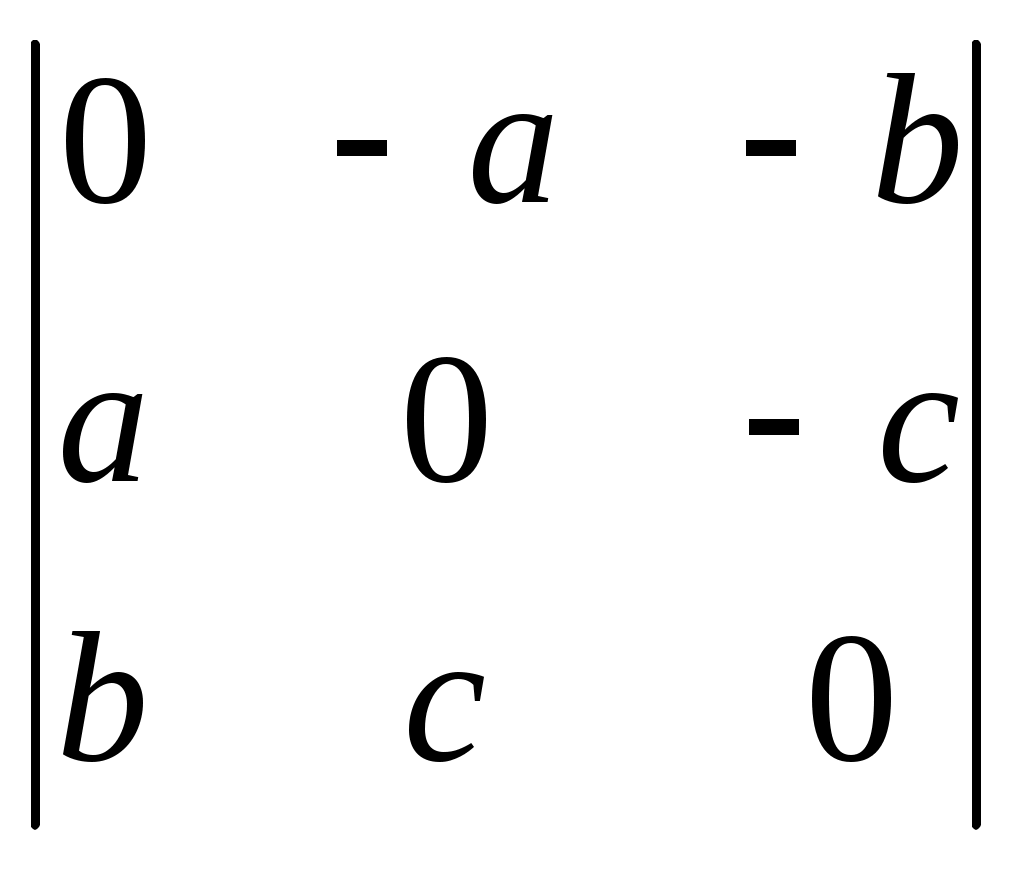 =0 =0В задачах 1223—1227 требуется вычислить определители, пользуясь одним свойством 9. 1223. 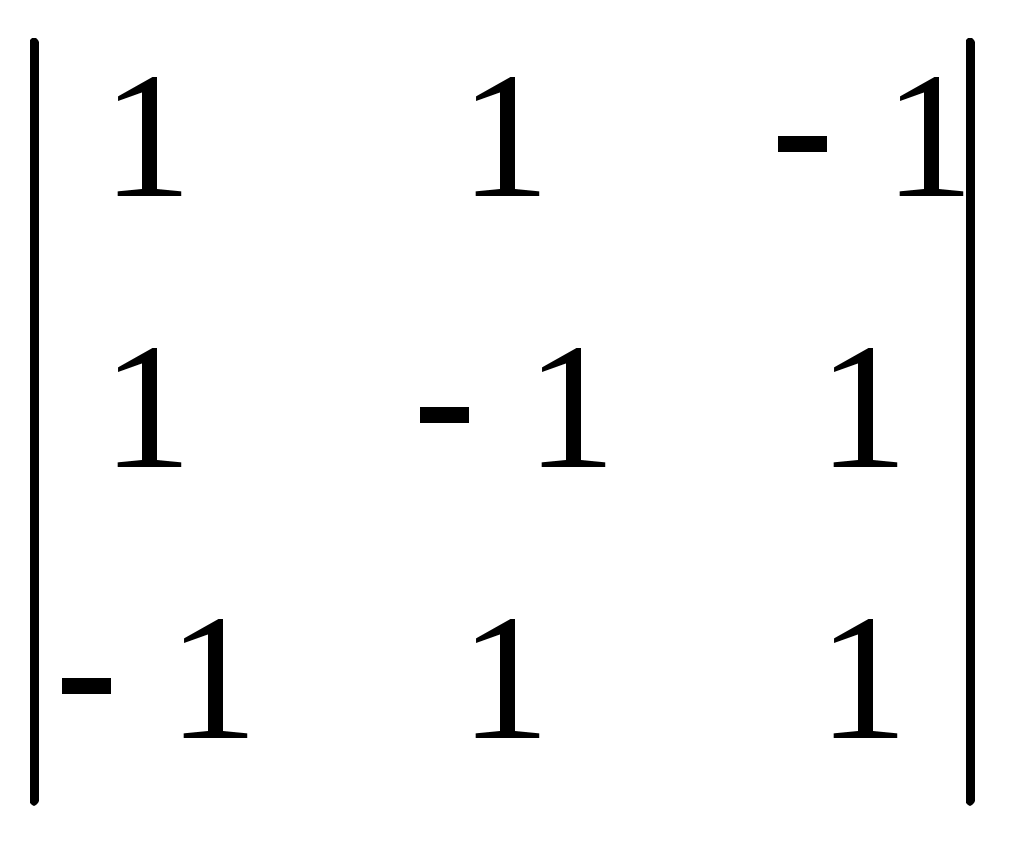 . 1224. . 1224.  . .1225. 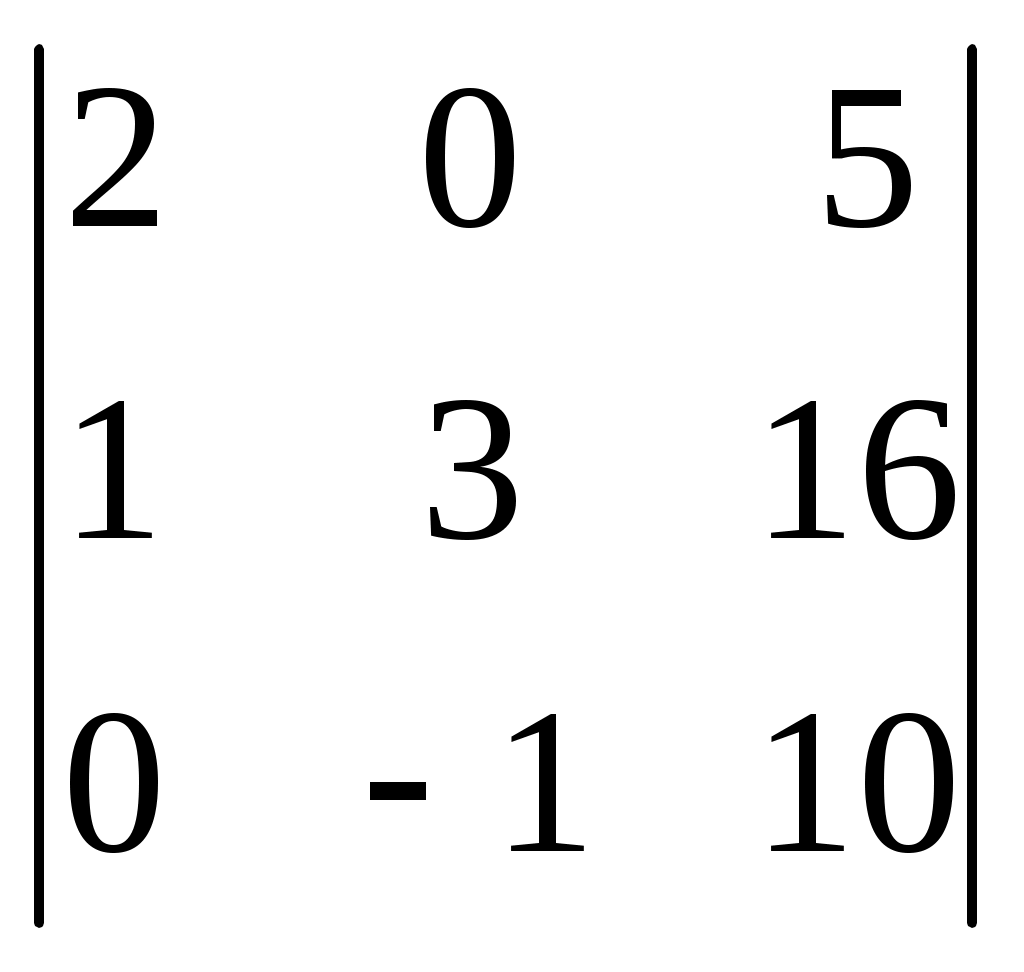 . 1226. . 1226. 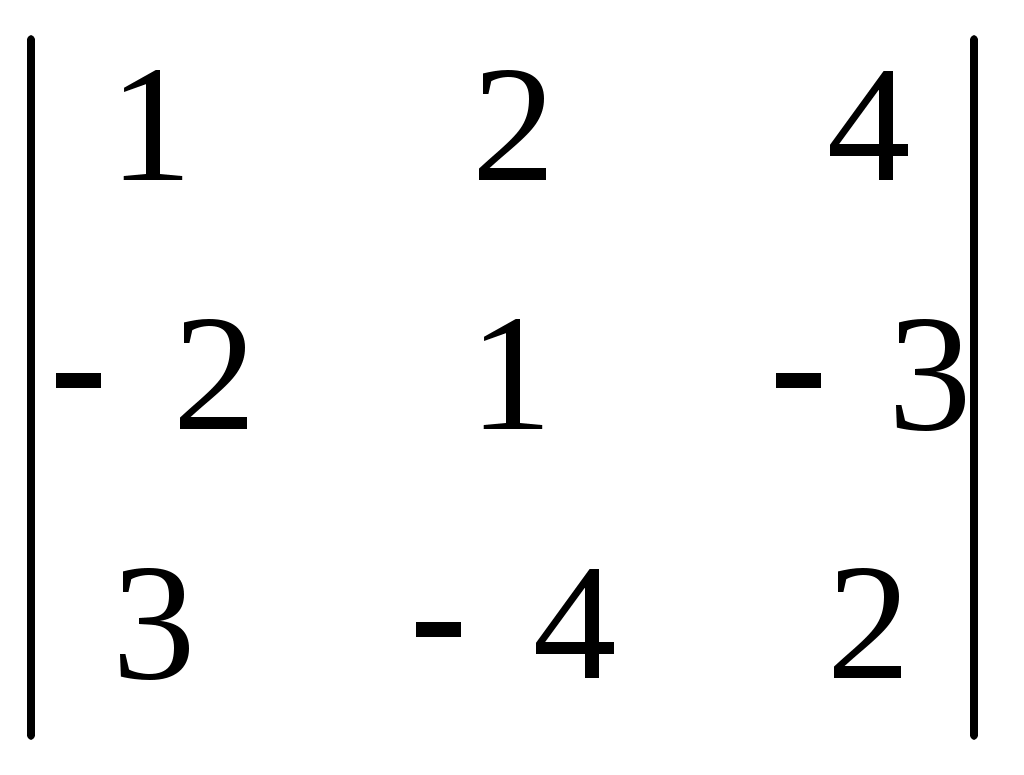 . .1227. 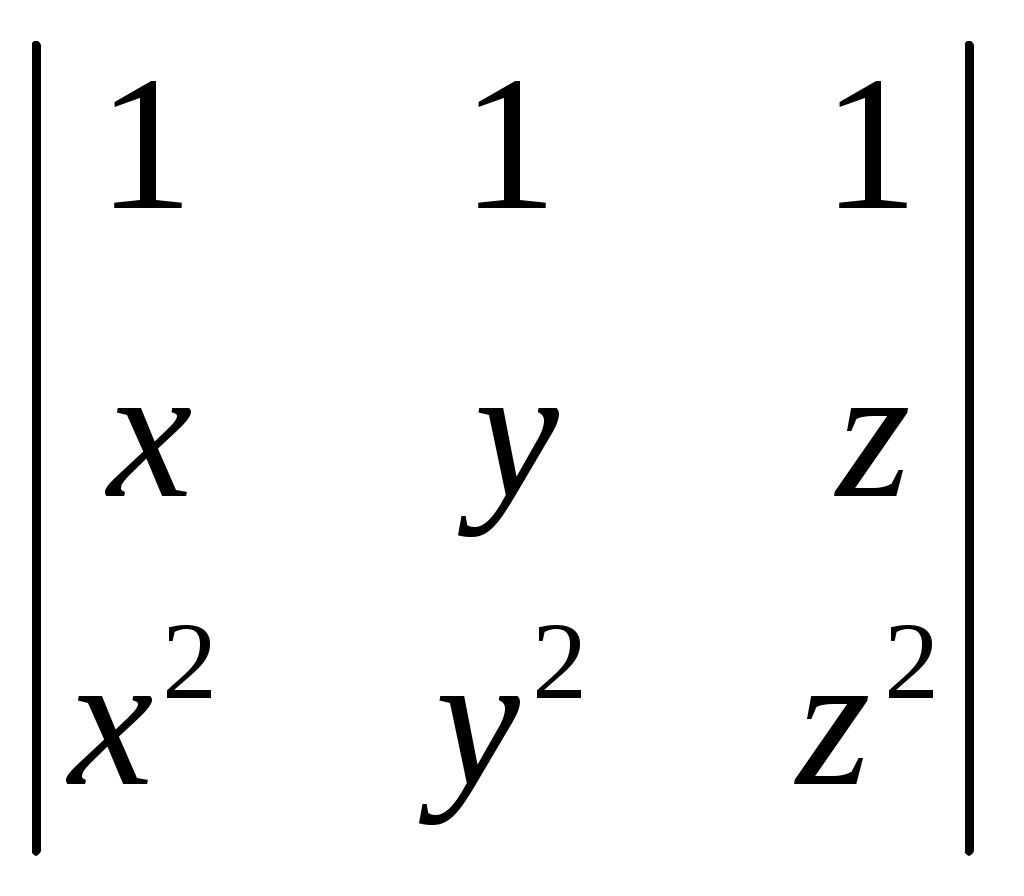 . .1228. Определители, данные в задачах 1223—1227, пользуясь свойством 8, преобразовать так, чтобы в каком-либо столбце (или строке) определителя два элемента стали равными нулю, а затем вычислить каждый из них, воспользовавшись свойством 9. В задачах 1229—1232 требуется вычислить определители. 1229.  . 1230. . 1230. 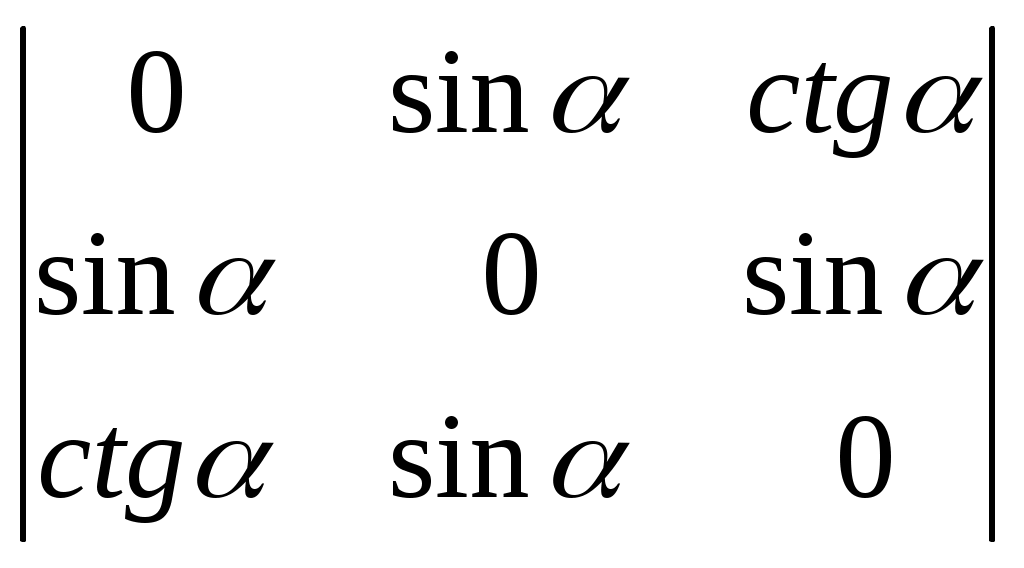 1231. 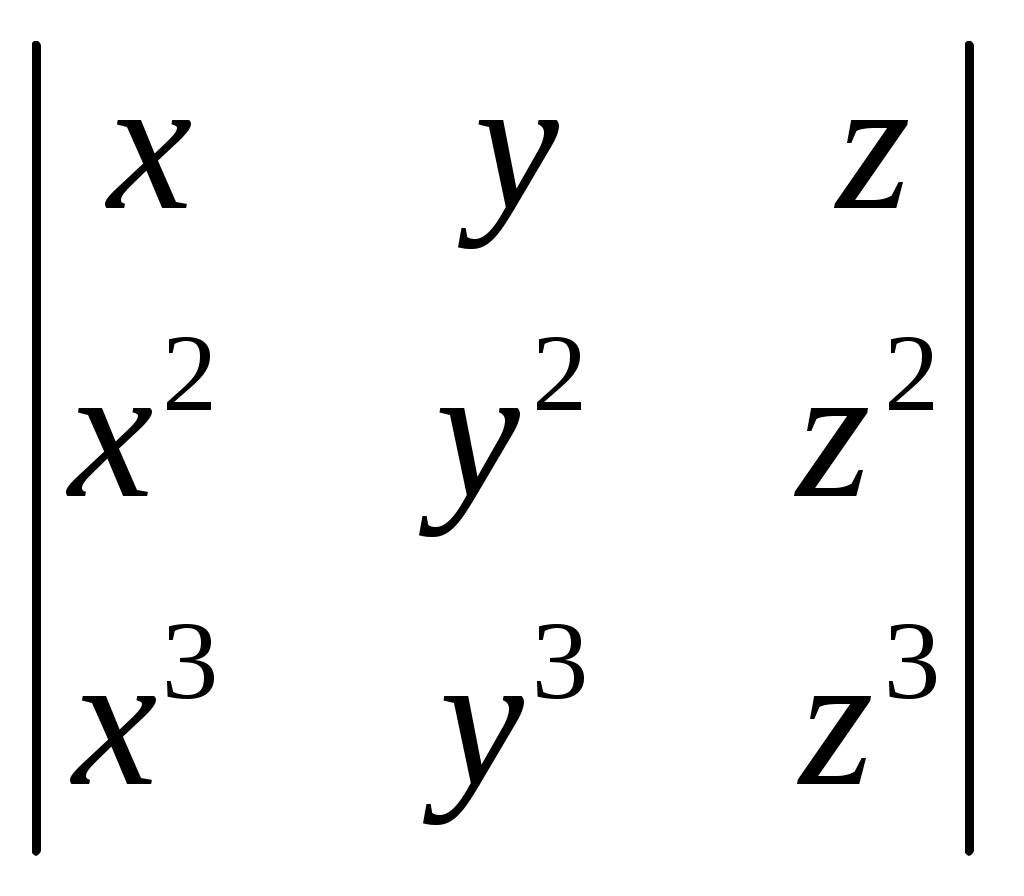 . 1232. . 1232.  . .1233. Доказать справедливость равенств: 1) 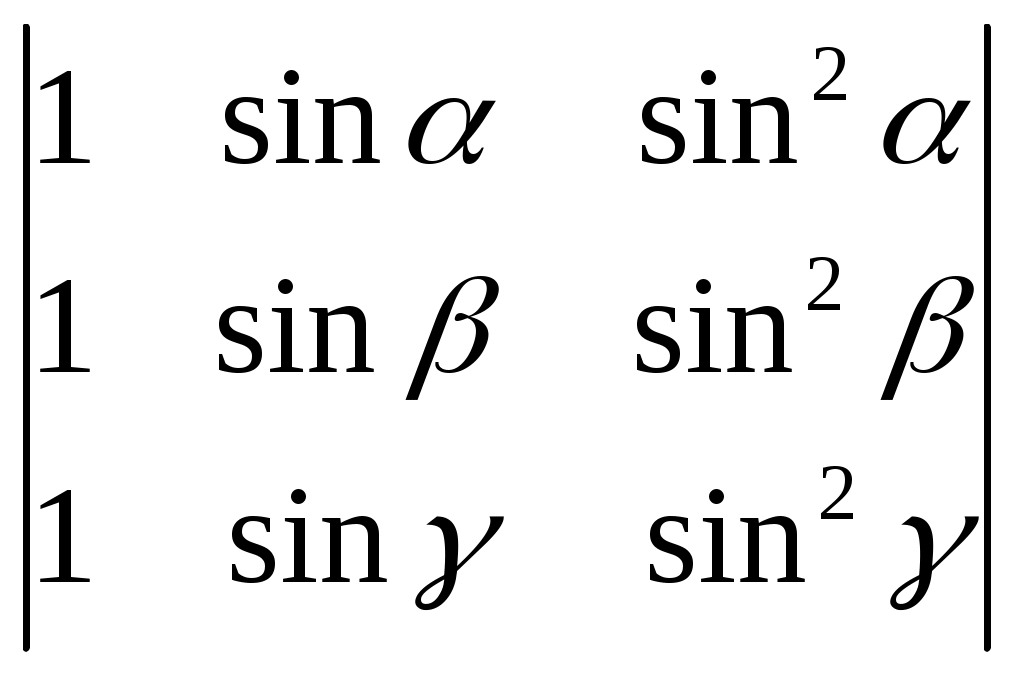 = (sin α — sin β) (sin β — sin γ)(sin γ — sin α); = (sin α — sin β) (sin β — sin γ)(sin γ — sin α);2) 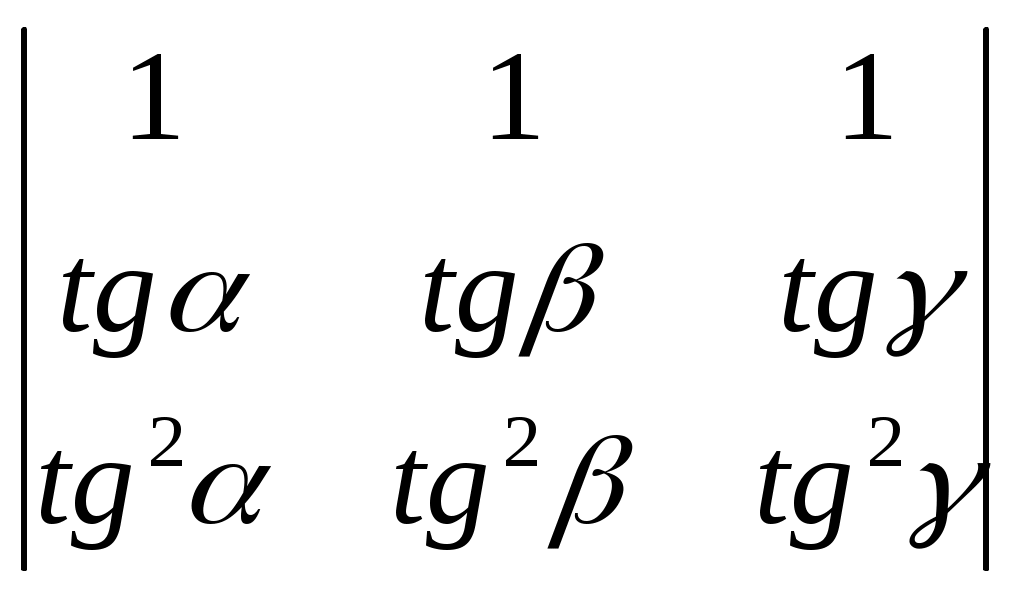 = = 1234. Решить уравнения: 1) 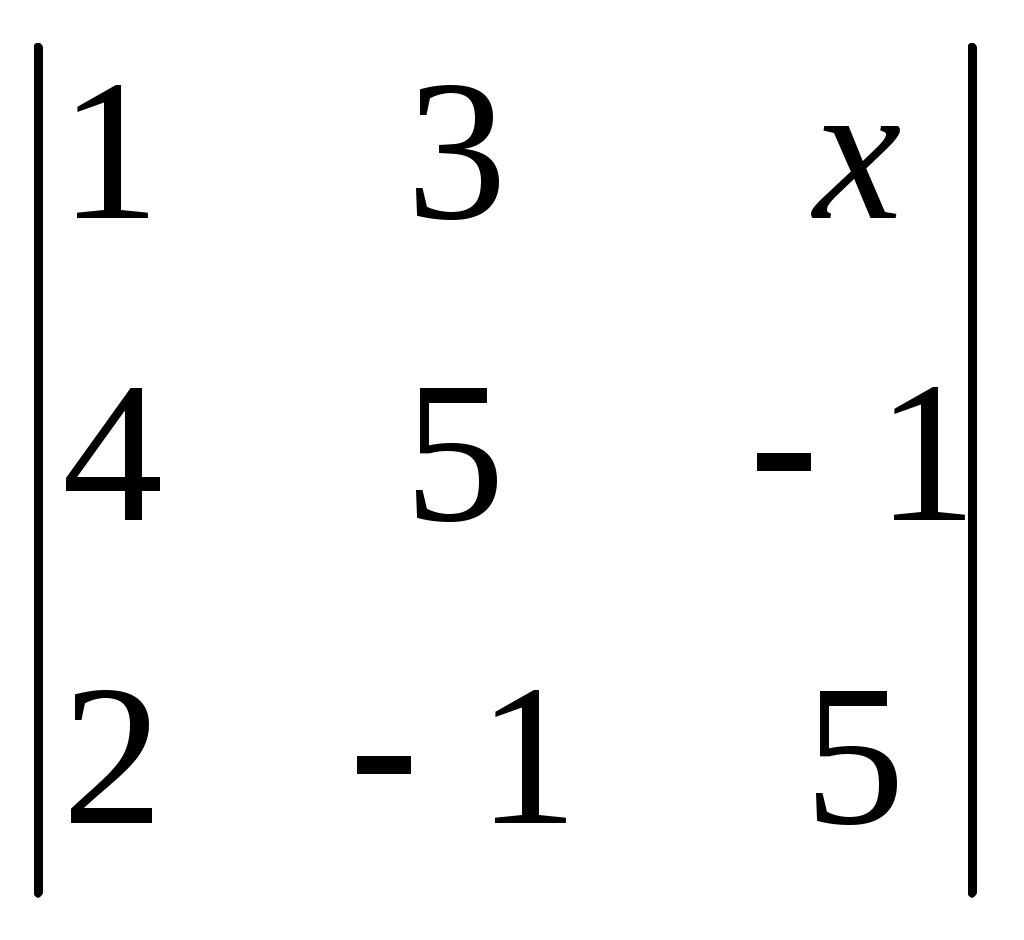 = 0 2) = 0 2) 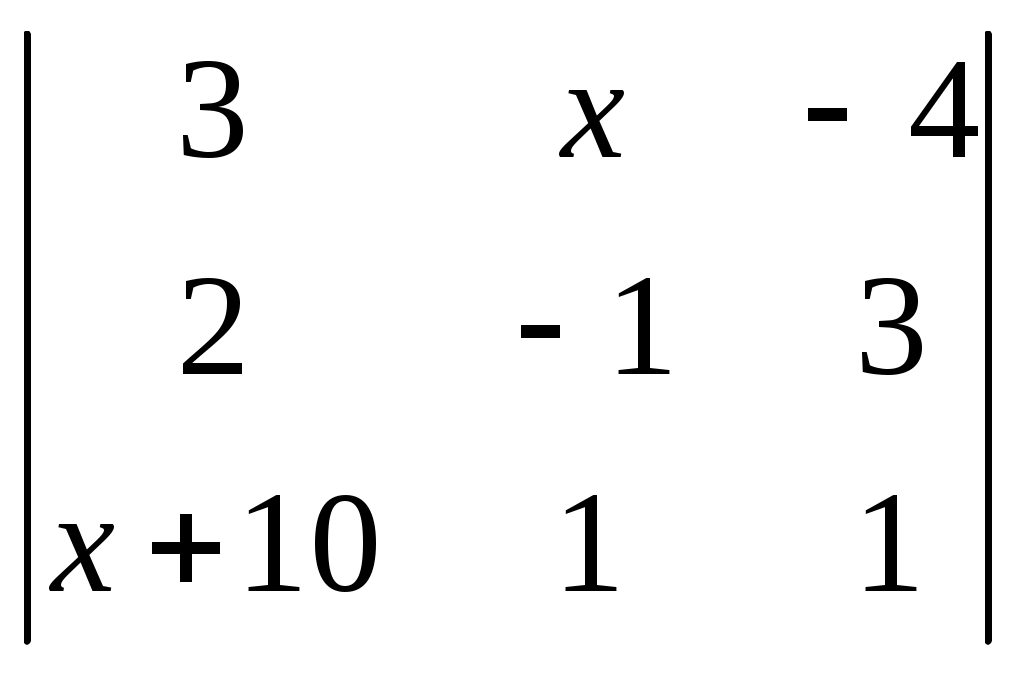 = 0 = 01235. Решить неравенства: 1) 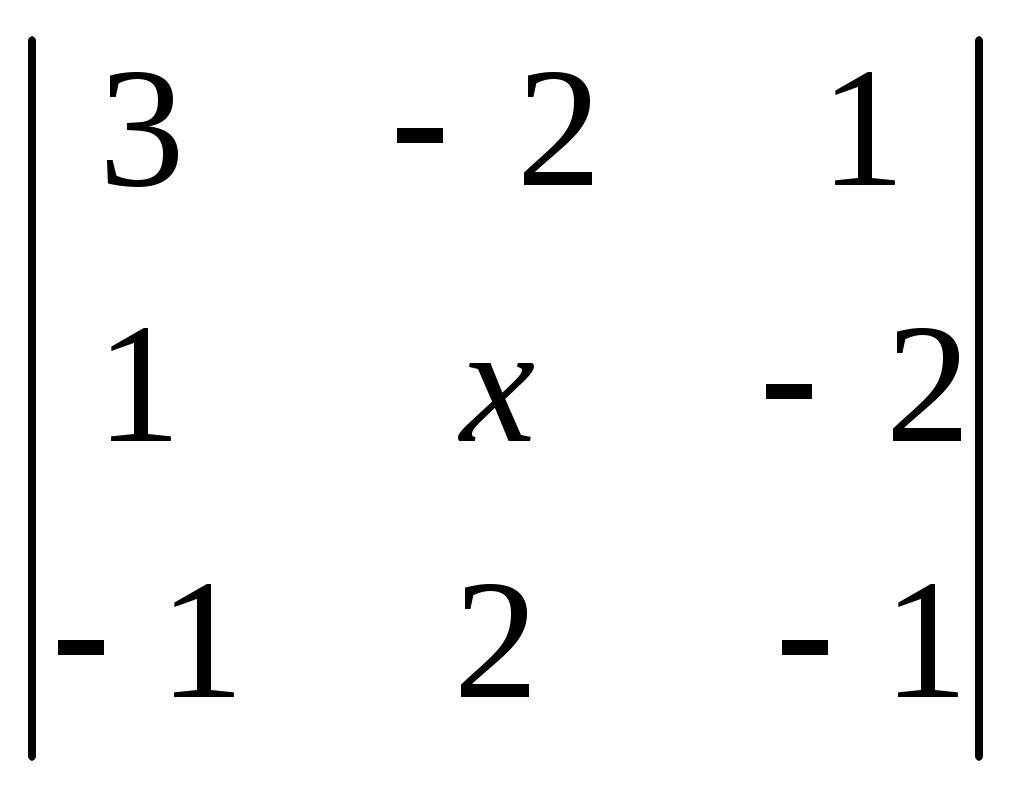 < 1 2) < 1 2) 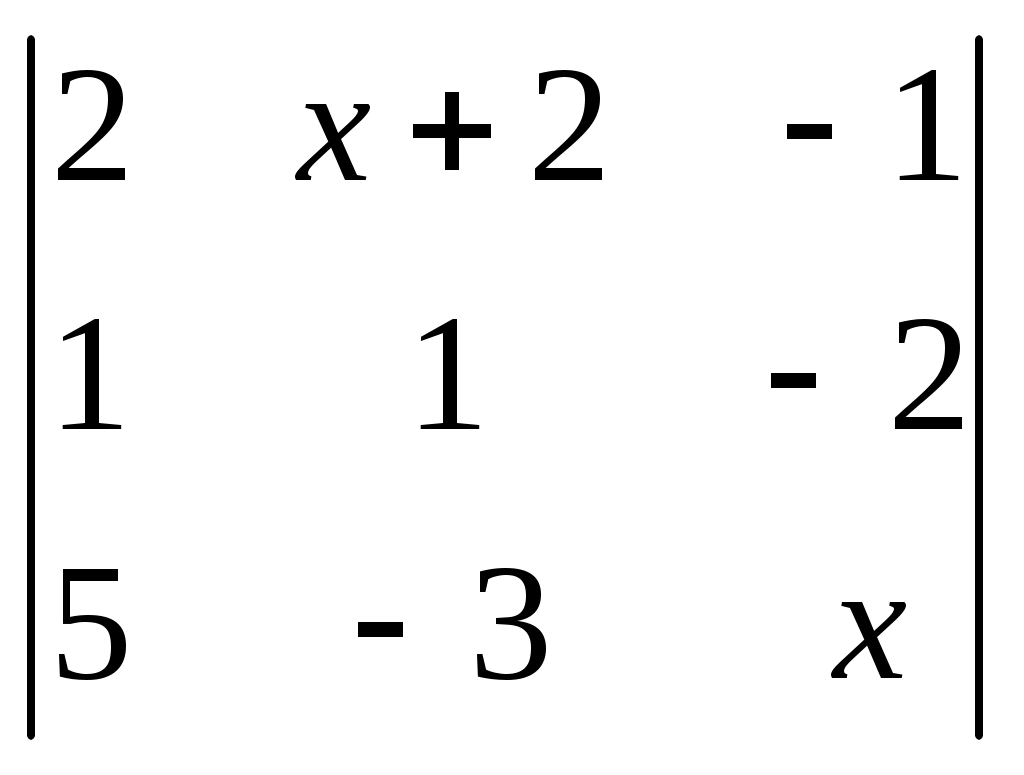 > 0 > 0 |
