ПЛАН УРОКА (1). План урока тема урока Определители 2 го и 3 го порядков. Свойства определителей
 Скачать 310 Kb. Скачать 310 Kb.
|
|
ПЛАН УРОКА Тема урока Определители 2го и 3го порядков. Свойства определителей. Решение систем двух (трех) уравнений по формулам Крамера. Цели урока: ОБРАЗОВАТЕЛЬНЫЕ: ознакомить с определителями квадратных матриц 2-го, 3-го порядка; ознакомить с определением систем линейных уравнений и научить решать системы линейных уравнений методом Крамера . РАЗВИВАЮЩИЕ: развивать навыки умения вычислять определители 2-го, 3-го порядка, развивать интерес к предмету, активизировать мыслительную деятельность; ВОСПИТАТЕЛЬНЫЕ: развитие умения применять полученные знания в профессиональной деятельности; Тип урока теоретическое занятие Методы обучения словесные План урока 1. Организационный момент: а) взаимное приветствие; б) фиксирование присутствия студентов; в) постановка цели занятия перед студентами; г) готовность и настрой студентов на работу в течение урока. 2. Проверка домашнего задания. 3. Изложение нового материала 4. Закрепление и совершенствование знаний. 5. Итоги урока. 6. Домашнее задание. Ход урока. Проверка домашнего задания. Фронтальная проверка домашнего задания. (задания вызвавшие затруднения вынести на доску и разобрать.) Изложения нового материала: 1. Понятие определителей. 2. Методы вычисления определителей 2-го,3-го порядка 3. Решение систем линейных уравнений методом Крамера. Закрепление и совершенствование знаний 1. Решение задач. [ 2]- №№ 1.32-1.36, [ 5]- №№ - 3-10,[ 2]- №№ 72-76 2. Самостоятельная работа . Итоги урока Оценка работы группы и отдельных студентов. Аргументация выставленных отметок, замечания по уроку. Домашнее задание: [ 2]- № 1.29-1.31, [ 5]- №№ - 17-20. [ 2]- 2.10, 2.11, 2.14, 2.16 . Теоретический материал к уроку Тема: Определители 2го и 3го порядков. Свойства определителей. Решение систем двух (трех) уравнений по формулам Крамера. Первые упоминания об определителях относятся к концу 17-го века, когда немецкий математик Лейбниц изучал линейные уравнения с многими неизвестными. Далее в конце 18-го века швейцарский математик Крамер указал общий закон составления определителей и привел формулы для решения систем линейных уравнений с n неизвестными с помощью определителей. В настоящее время нет почти ни одной отрасли математики, в которой не имели бы приложений определители. Они встречаются в алгебре, в аналитической геометрии, в механике, в теории функций, в линейном программирования и т.д. Определитель n-го порядка представляет собой квадратную таблицу, состоящую из n строк и n столбцов, и обозначается символом: 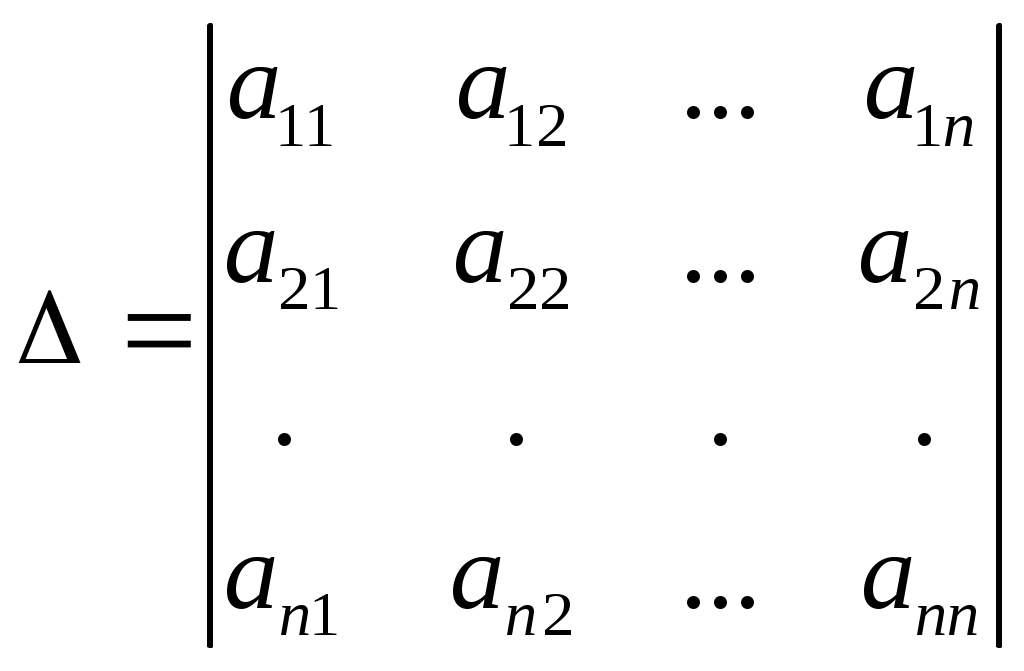 числа Диагональ определителя, состоящая из элементов с одинаковыми индексами, называется главной, а вторая называется побочной. Определителем n-го порядка называется число, являющееся алгебраической суммой n! членов, каждый из которых есть произведение n элементов, взятых по одному из каждой строки и из каждого столбца, причем знак всякого члена определяется входящими в его состав элементами. Определение 1. Определителем первого порядка называется элемент Определение 2. Определителем 2-го порядка называется число, которое вычисляется по формуле: Определение 3. Определителем третьего порядка называется число, которое вычисляется по формуле: 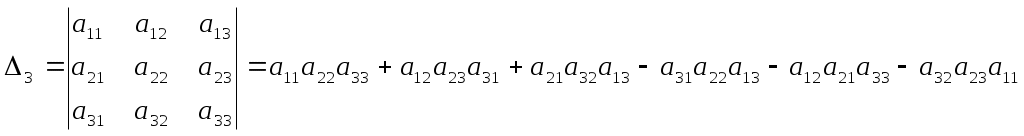 Для запоминания формулы используется правило Сарруса (правило «треугольников»): Пример 1. Вычислить определитель: Пример 2. Вычислить определитель: 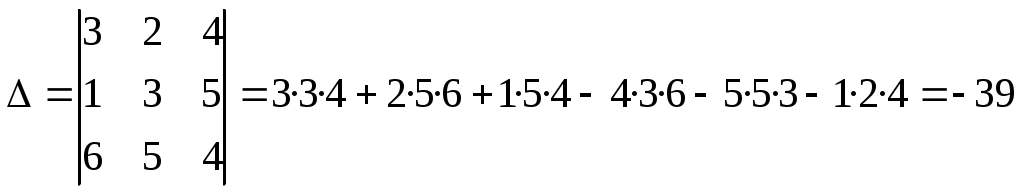 Правило Крамера. Составим определитель из коэффициентов при неизвестных системы (1), который называется определителем системы или главным определителем: 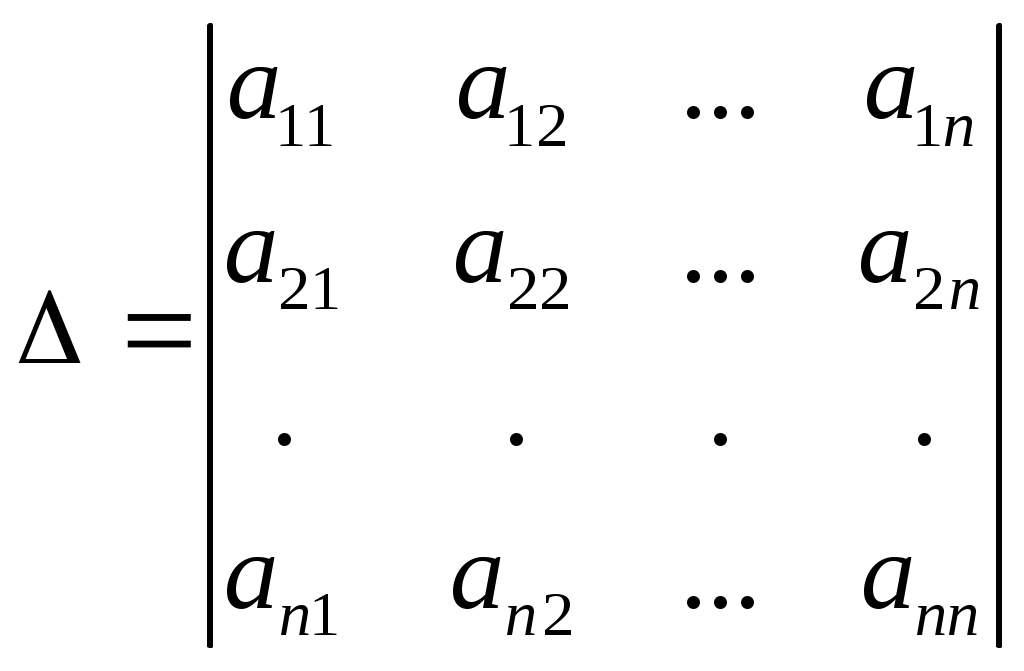 (2) (2)Если главный определитель где Пример 1. Решить систему по правилу Крамера. 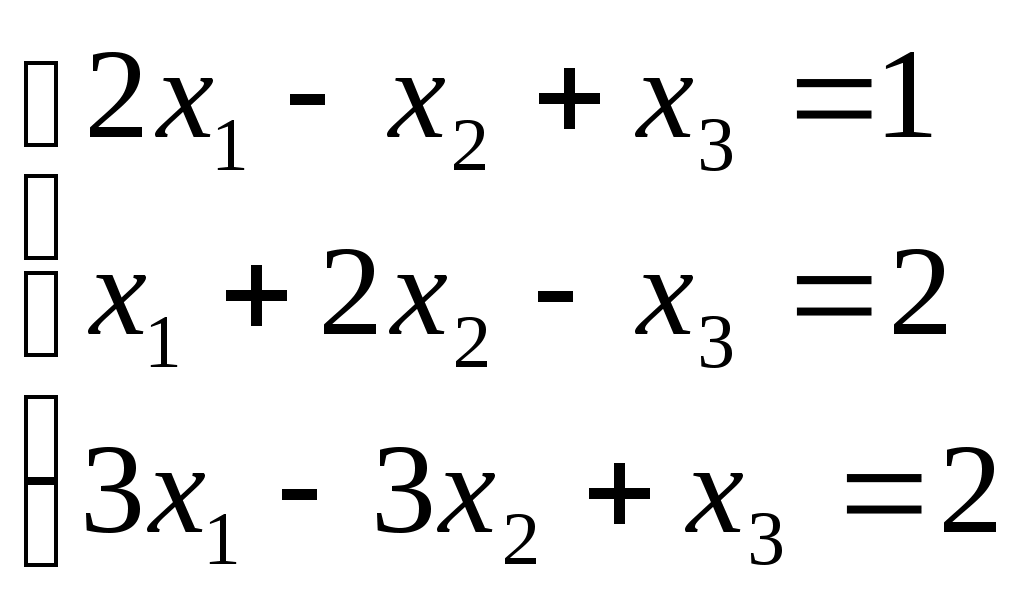 Решение:  . .Вычислим 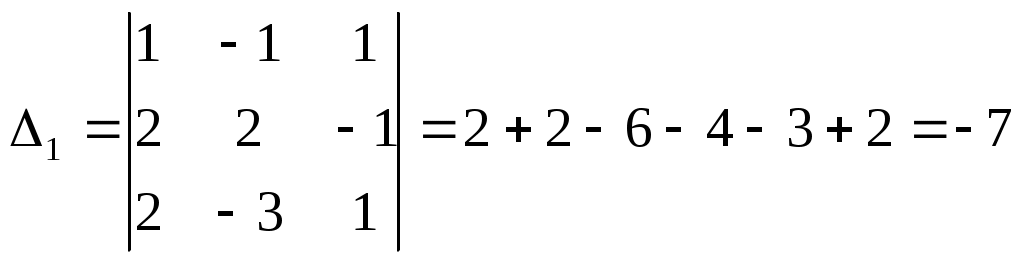 . .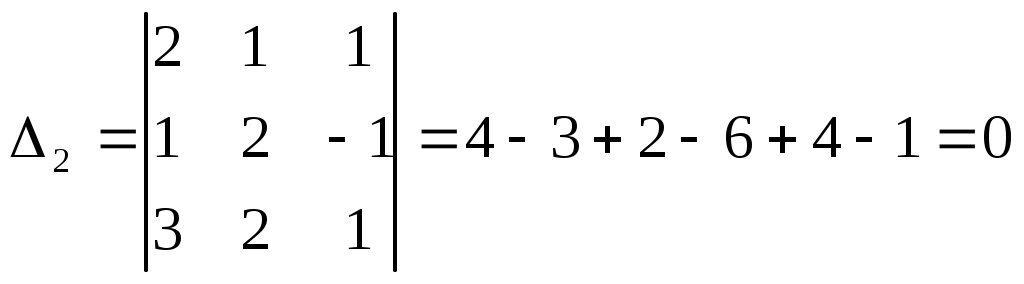 . .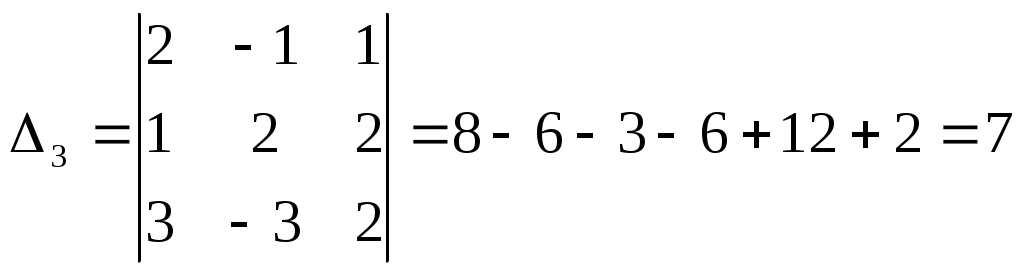 . .Тогда по формулам Крамера: 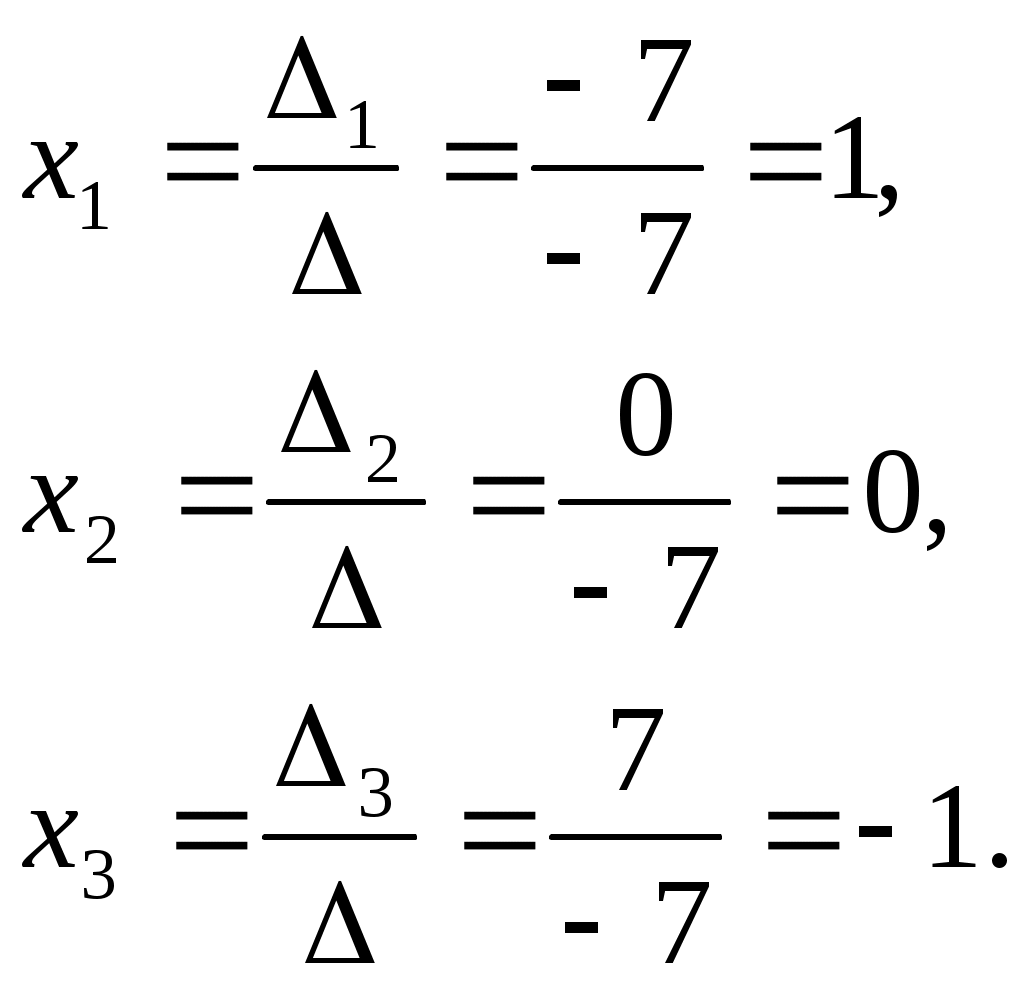 Ответ: Задачи для решения к уроку Вычислить определители третьего порядка: 1.32.  . 1.33. . 1.33.  . 1.34. . 1.34.  . .Доказать тождества: 1.35. 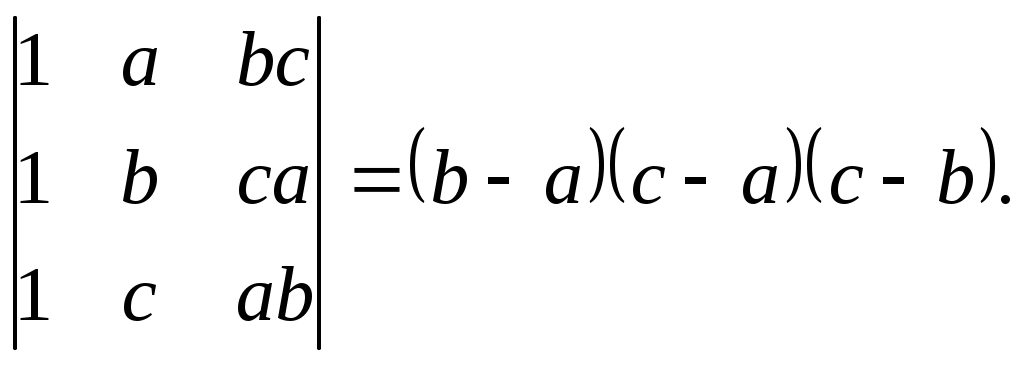 . 1.36. . 1.36. 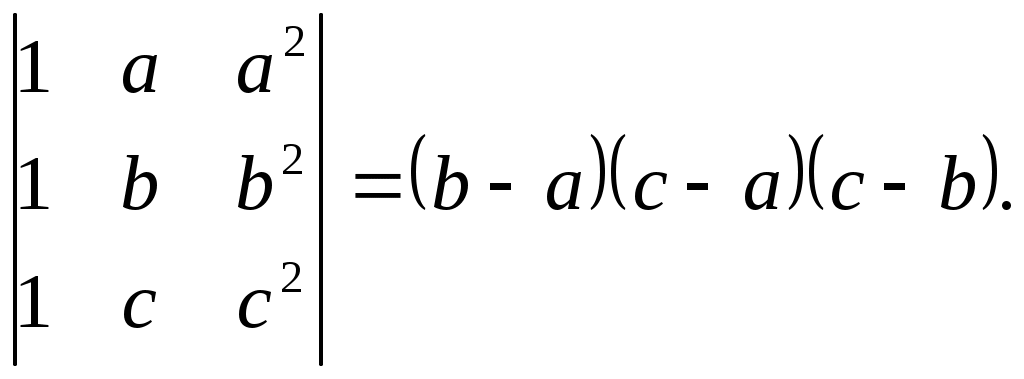 Вычислите следующие определители: № 3.  № 4. № 4.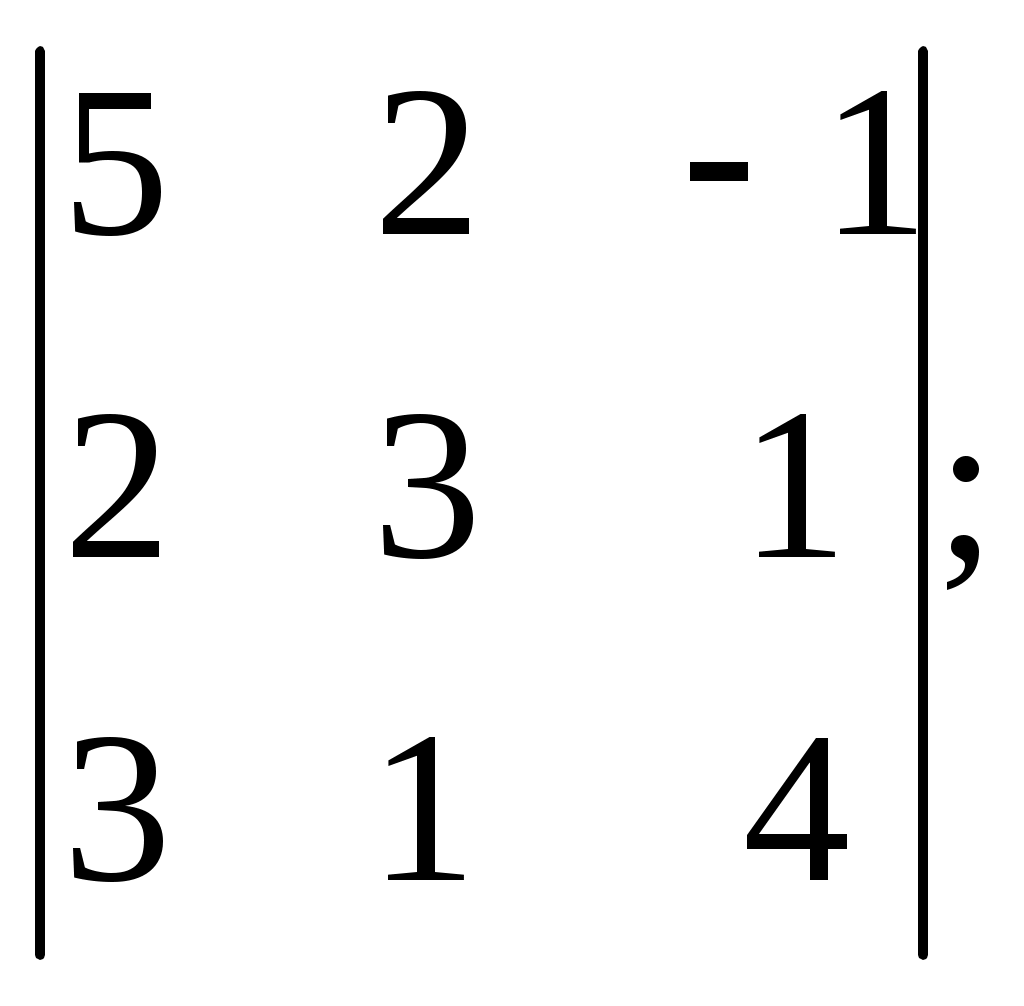 № 5. № 5.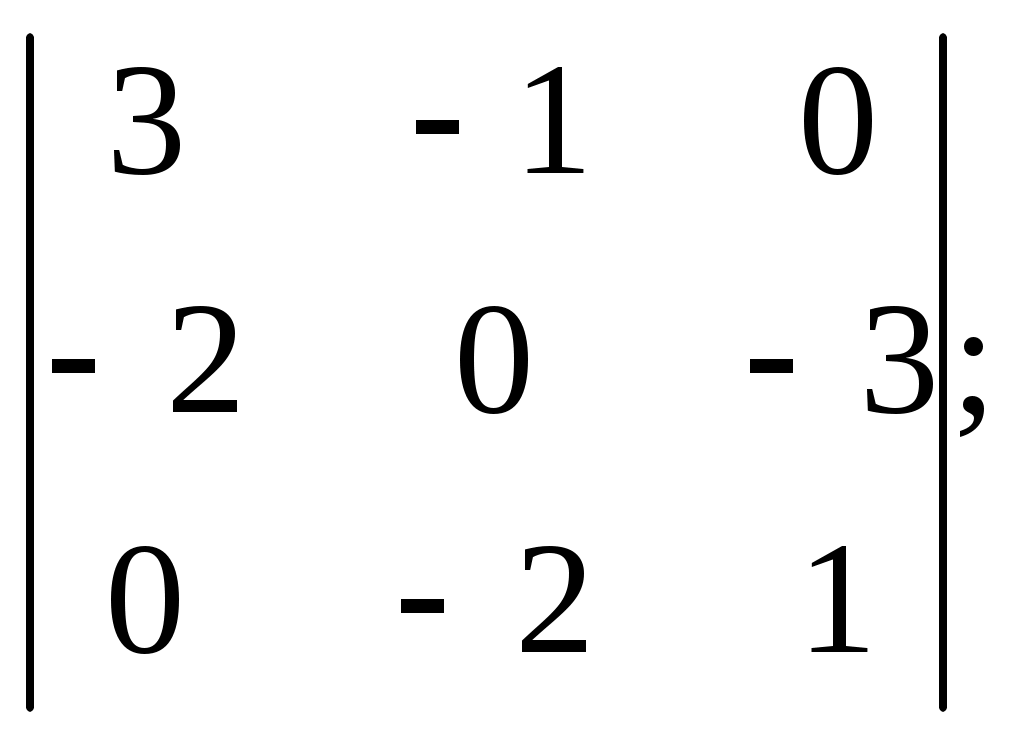 № 6. № 6.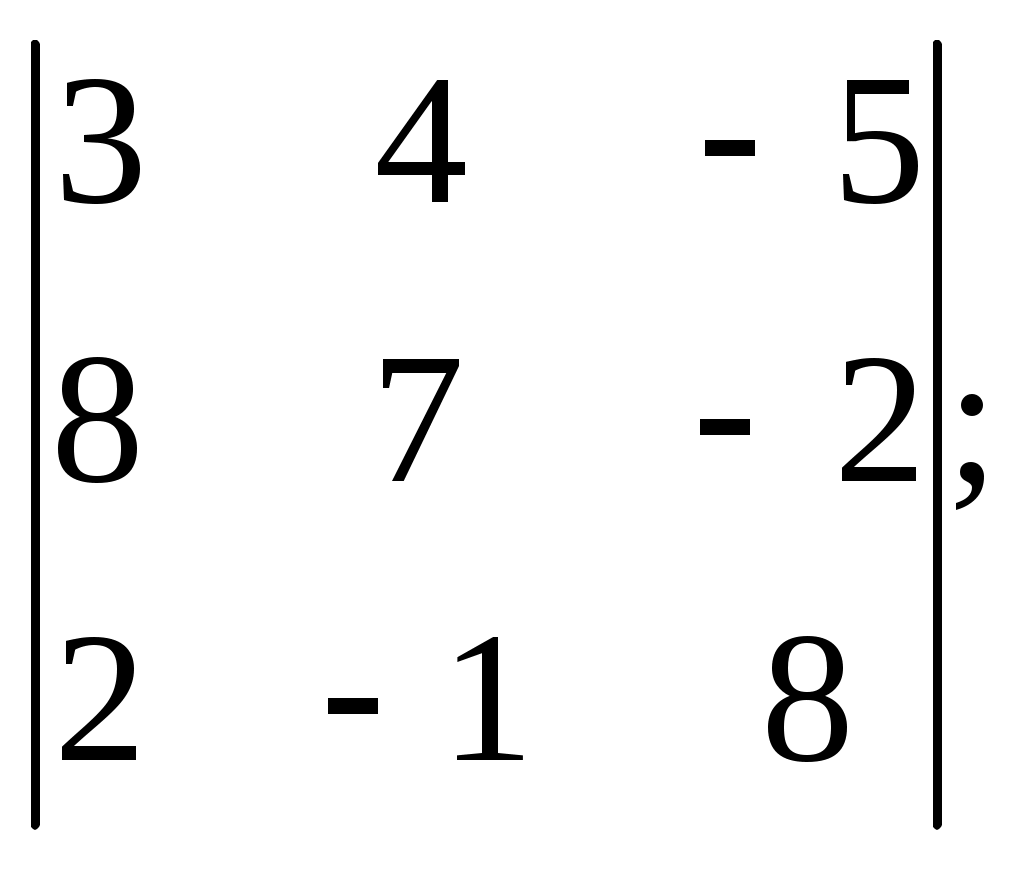 № 7.  № 8. № 8. № 9. № 9. № 10. № 10.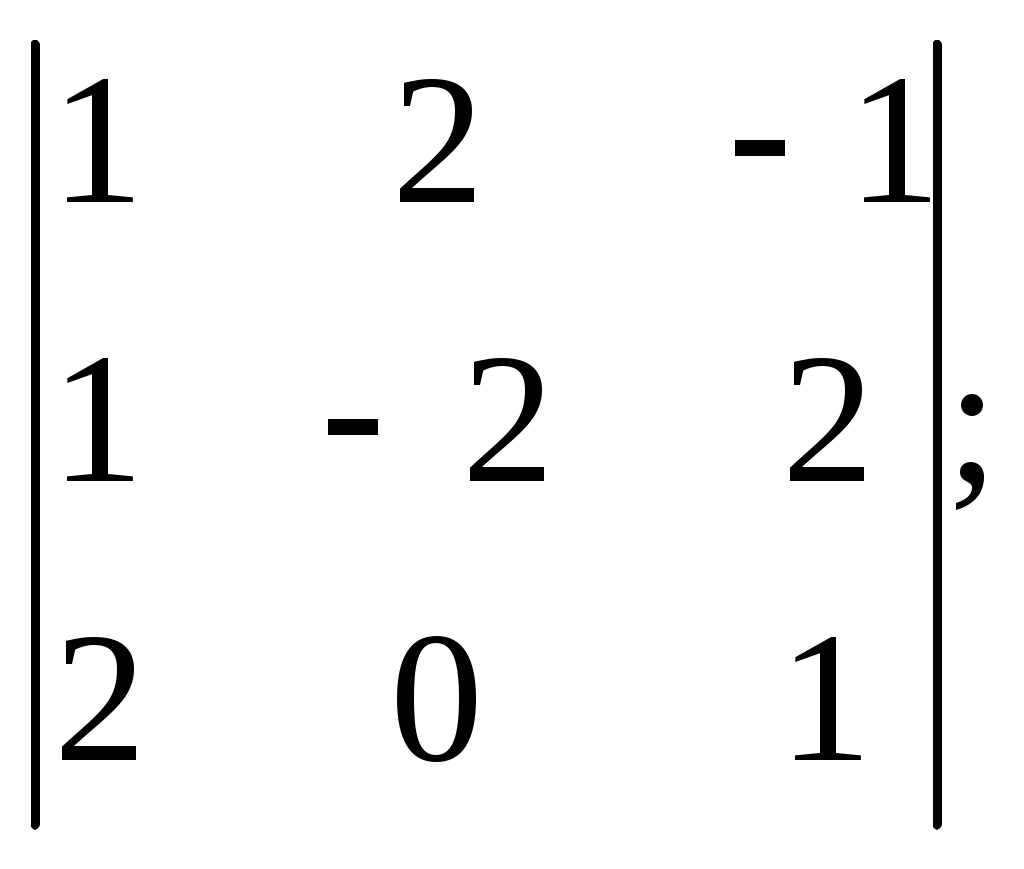 Решить системы уравнений, методом Крамера. № 72. 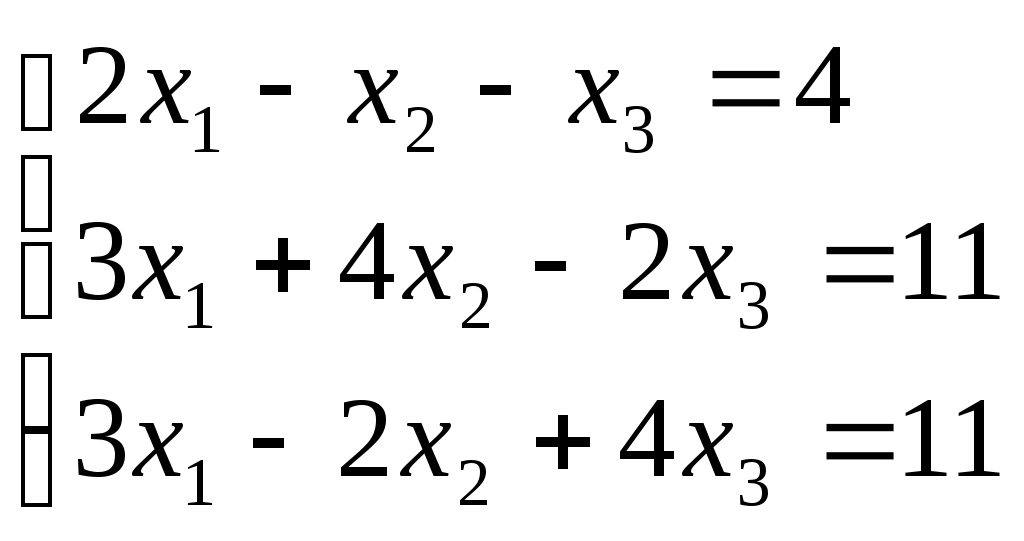 № 73. № 73. 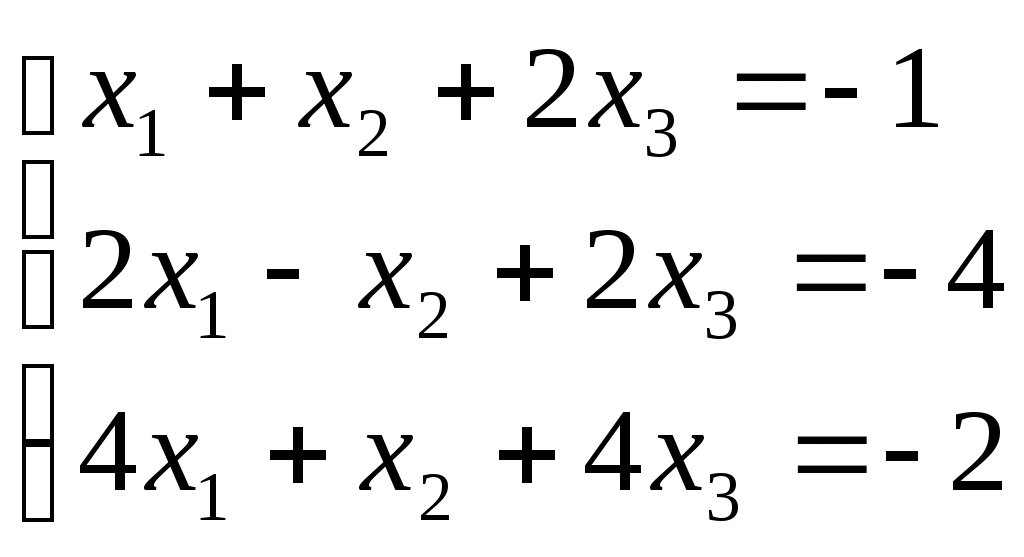 № 74. 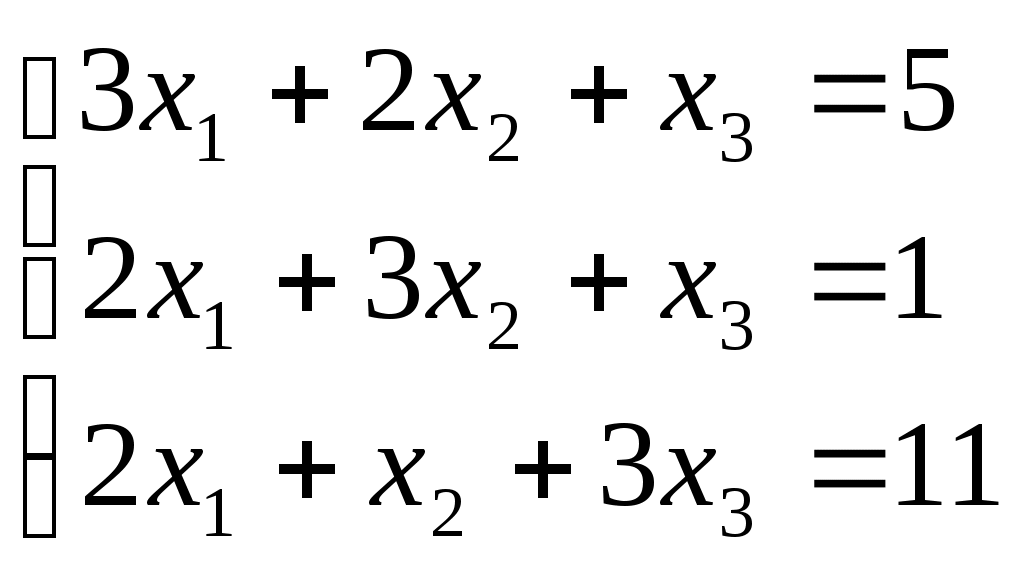 № 75. № 75. 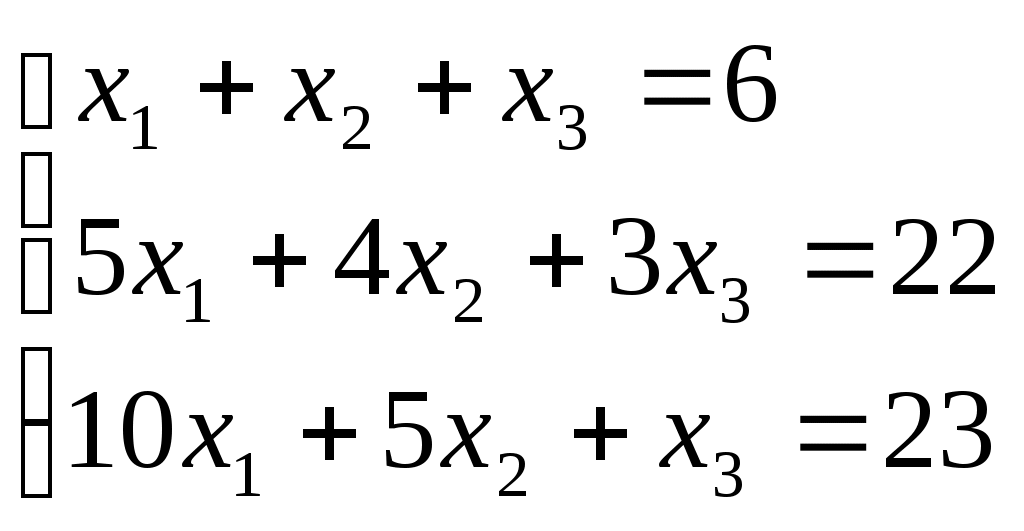 № 76. № 76. 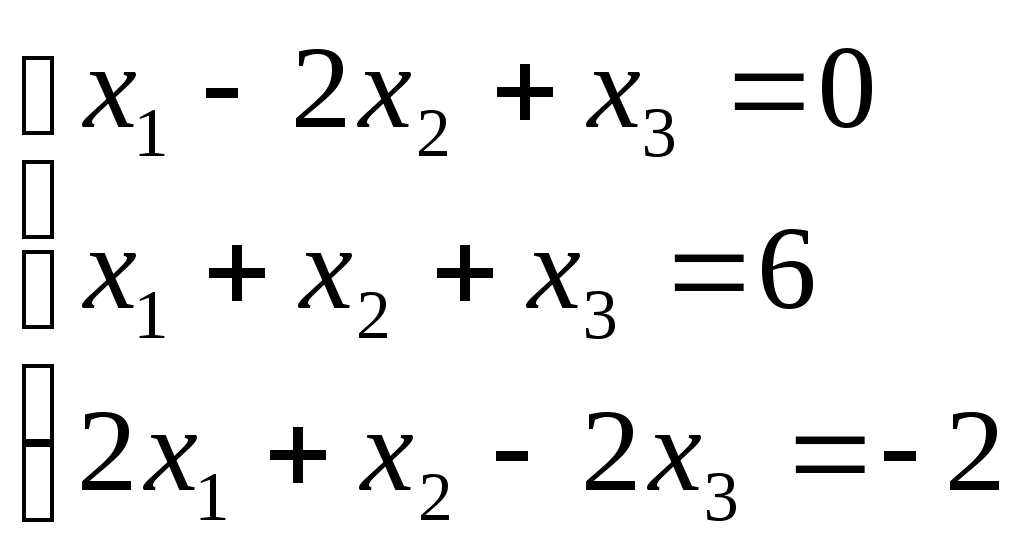 Домашнее задание к уроку № Вычислить определители второго порядка : 1.29. Вычислить определители третьего порядка: № 17. 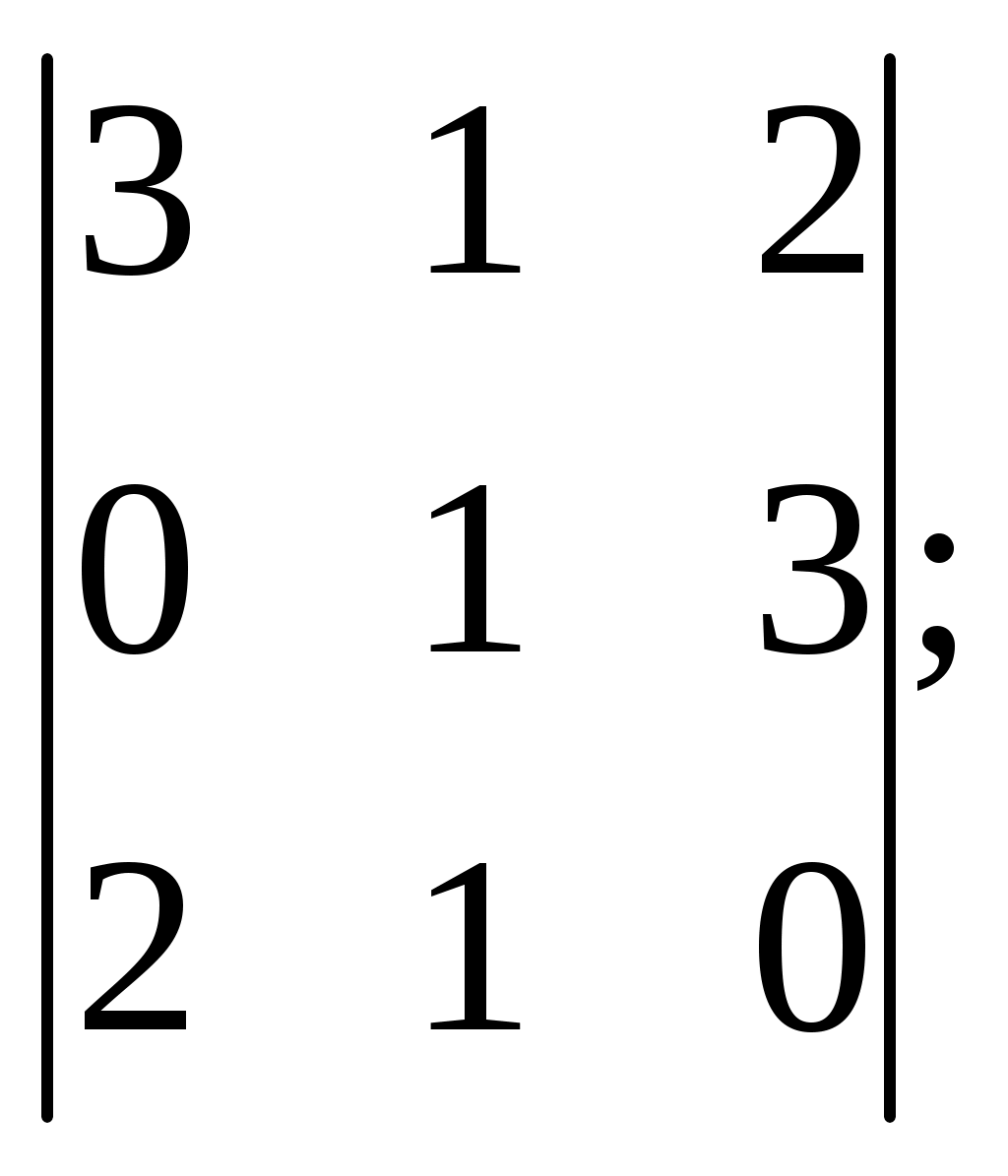 № 18. № 18. № 19. № 19.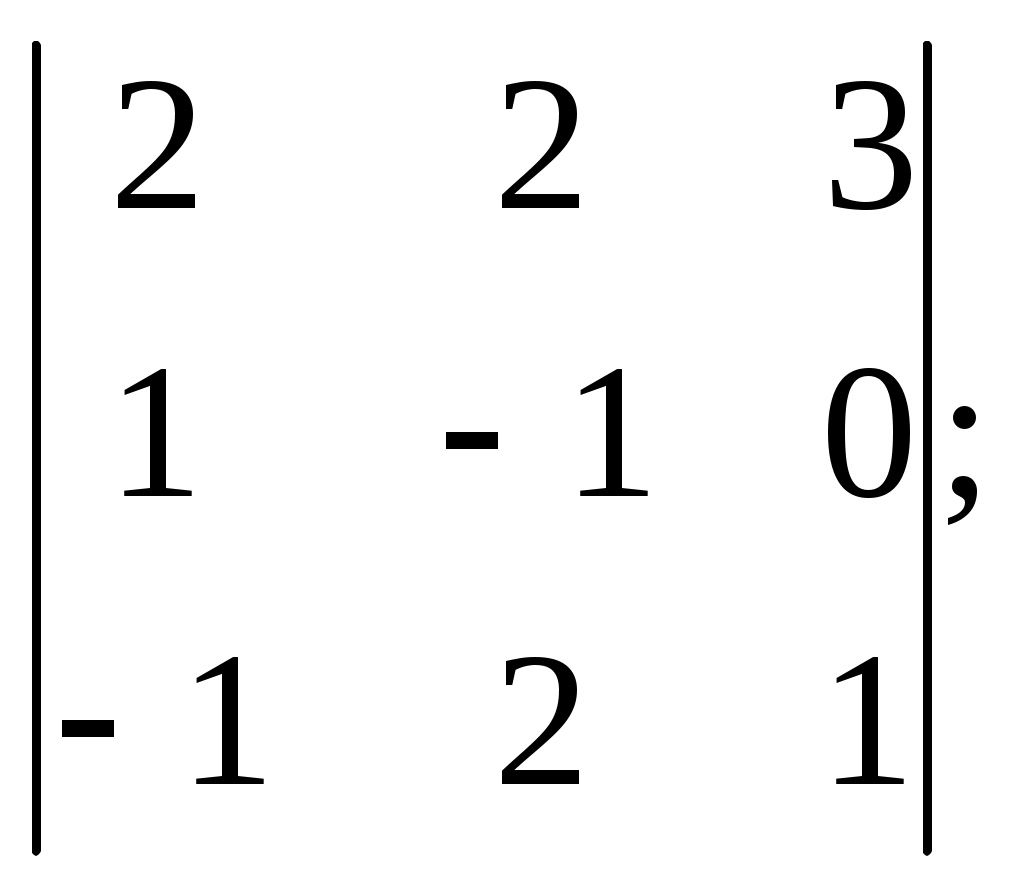 № 20. № 20. Решить системы уравнений методом Крамера . 2.10 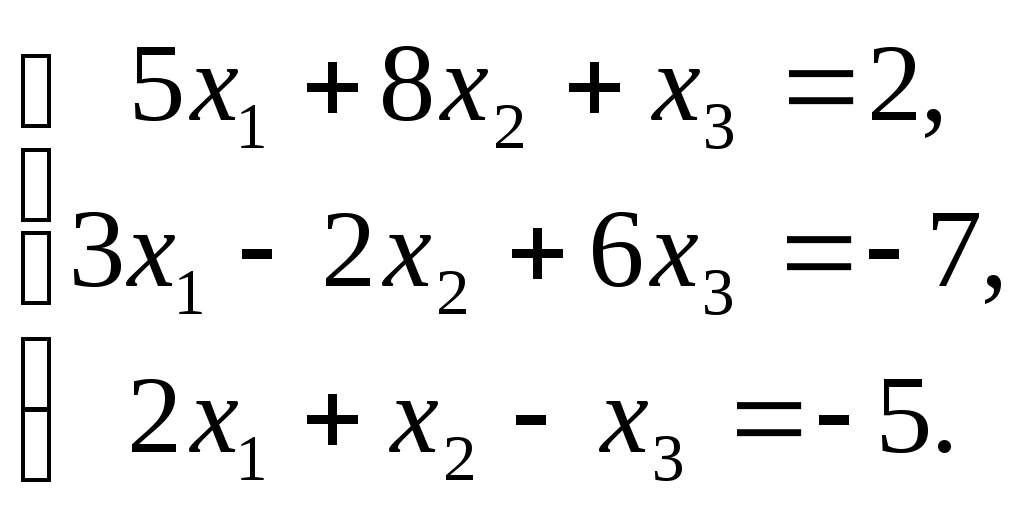 2.11 2.11 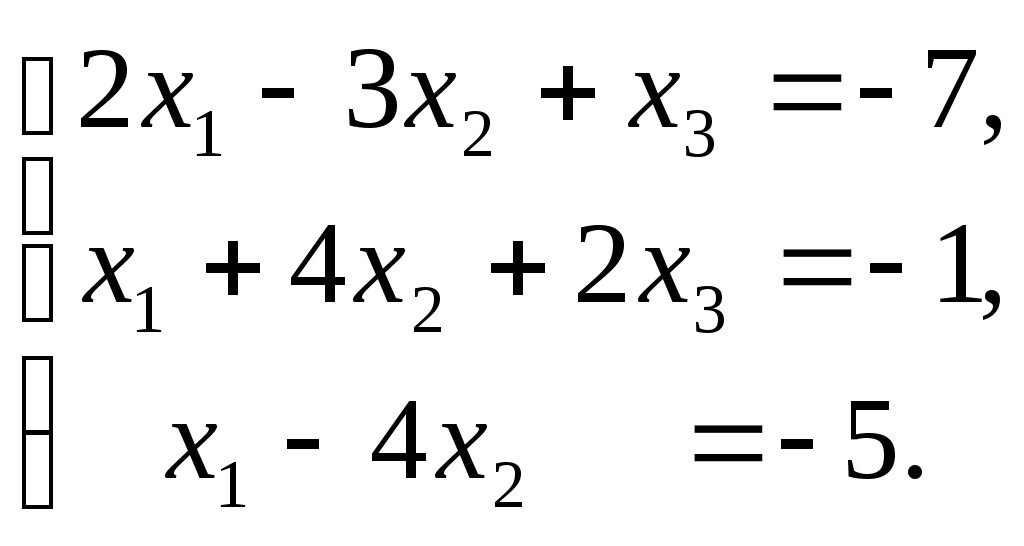 2.14  2.16 2.16 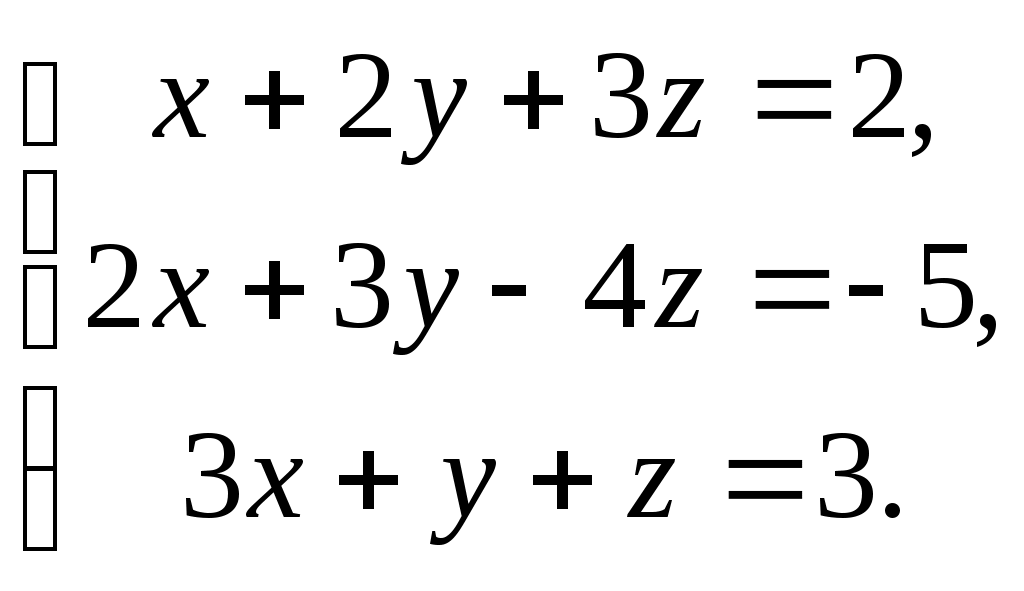 Самостоятельная работа к уроку Вариант №1. Решить систему уравнений : 1. 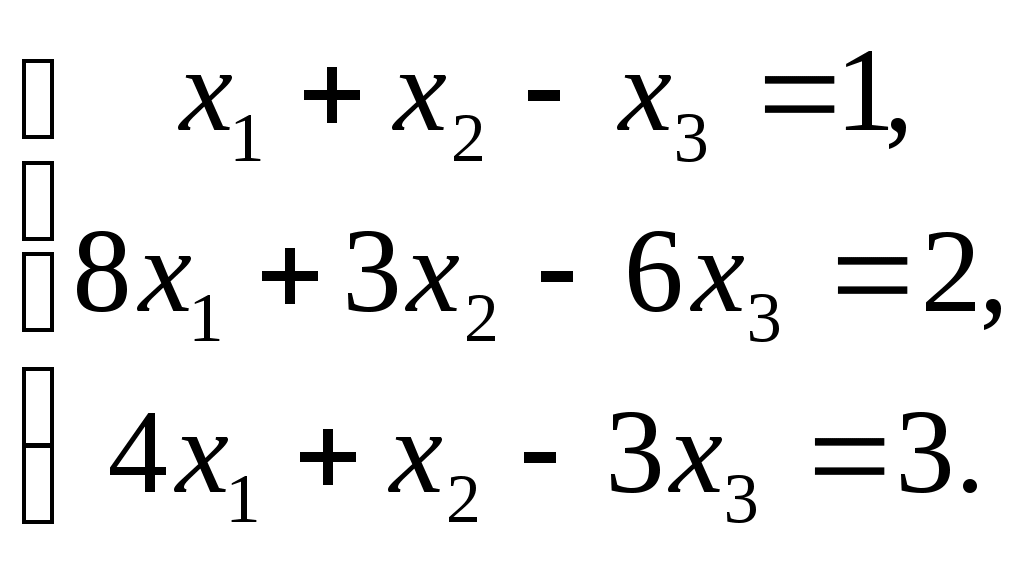 2. 2. 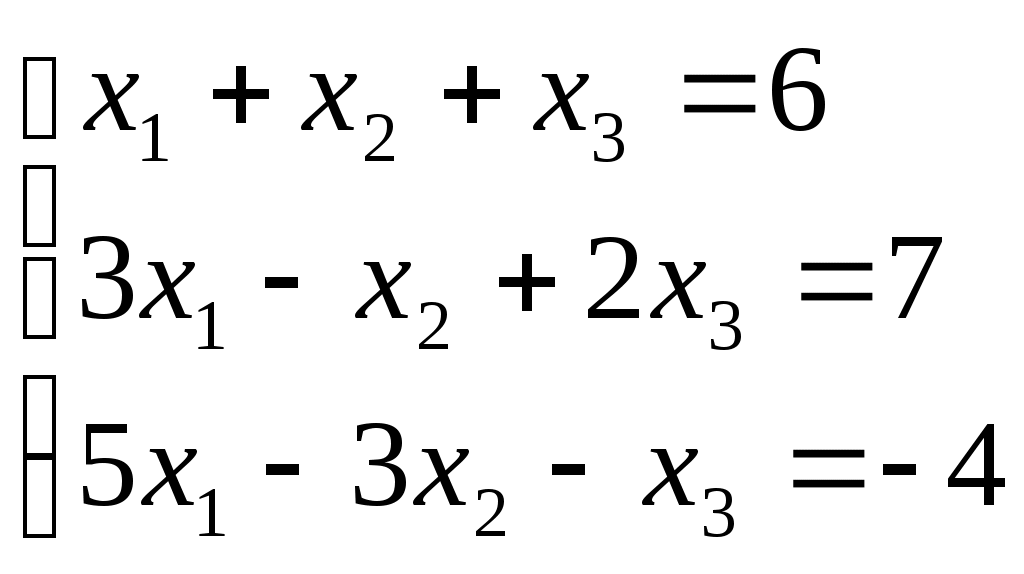 Вариант №2. Решить систему уравнений : 1. 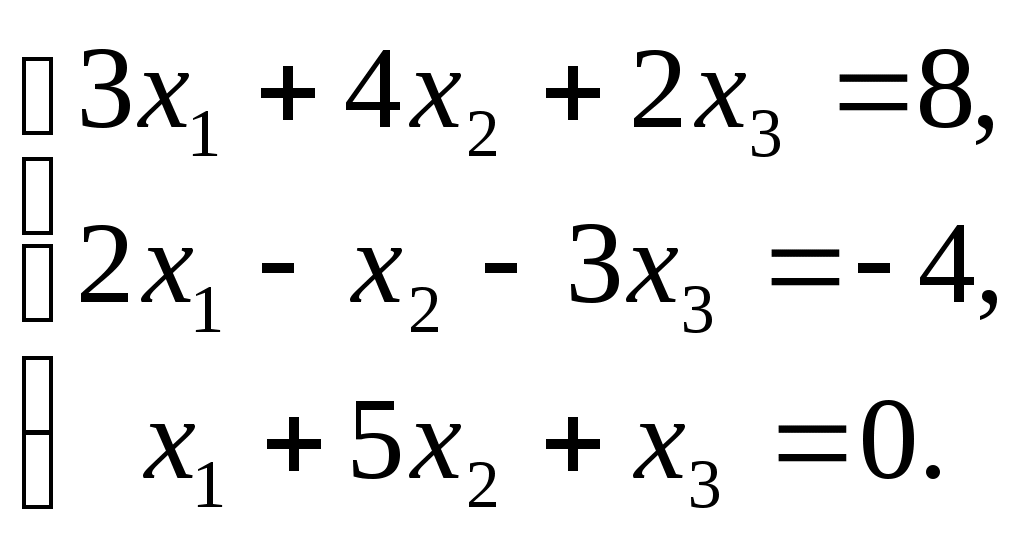 2. 2. 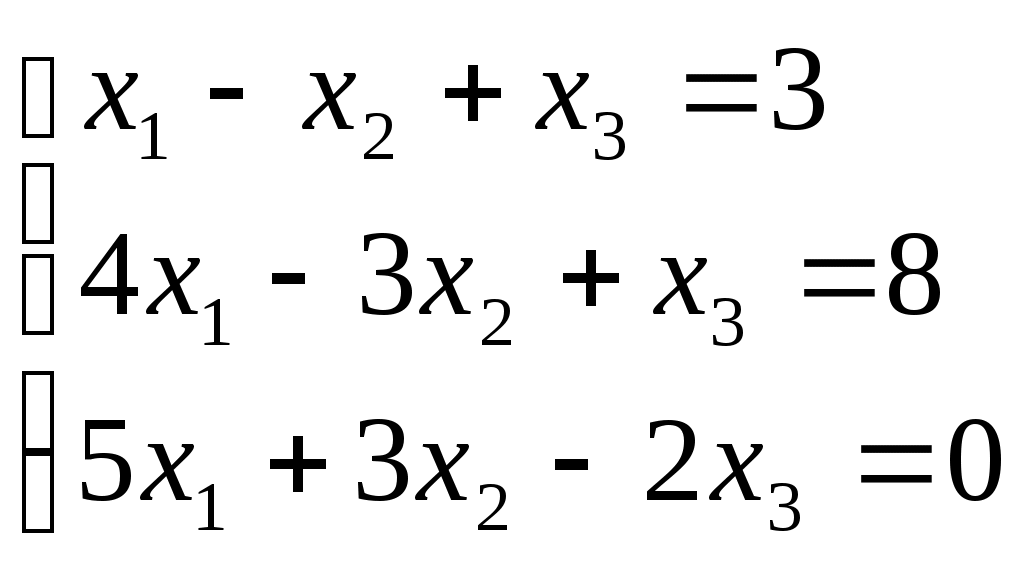 Вариант №3. Решить систему уравнений : 1. 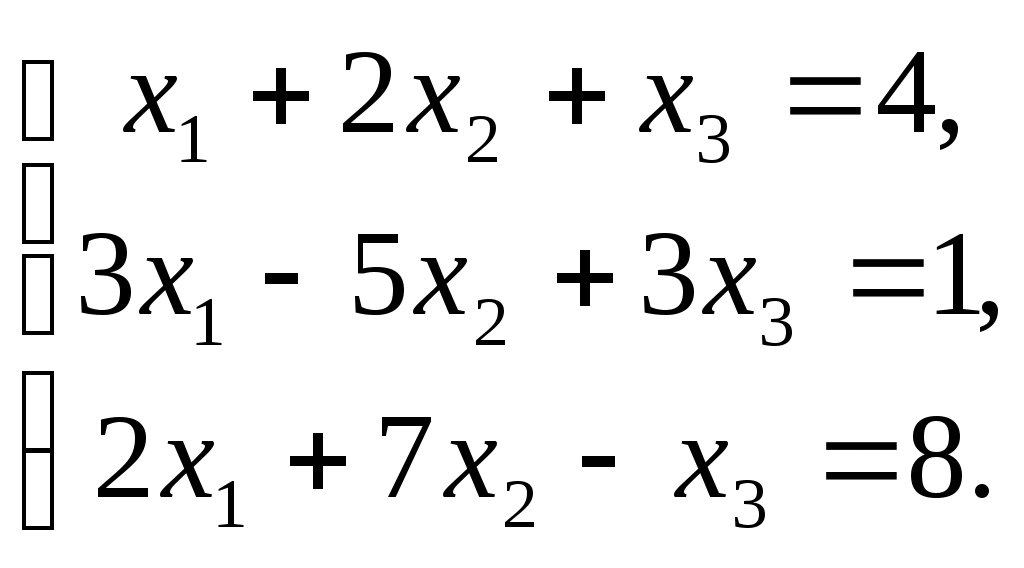 2. 2. 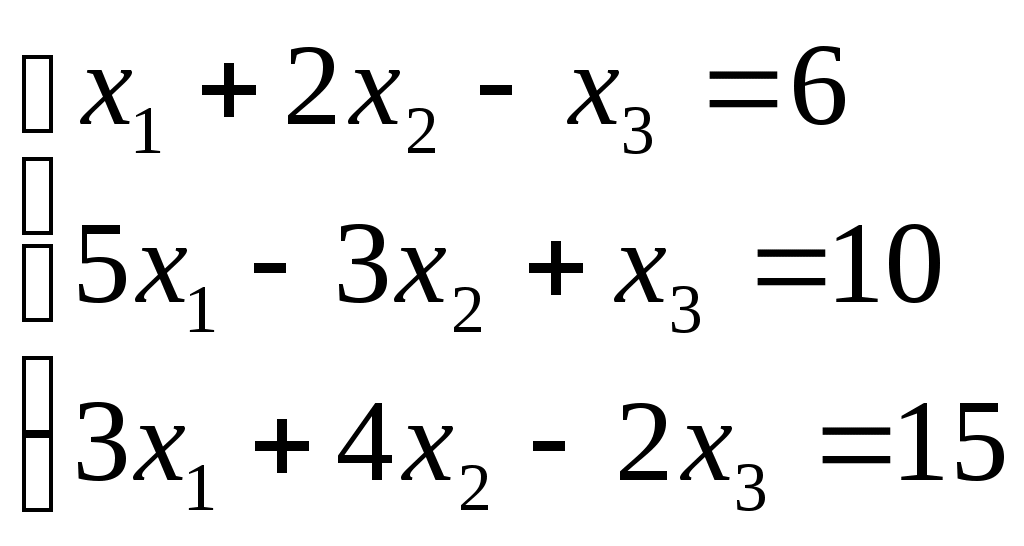 Вариант №4. Решить систему уравнений : 1. 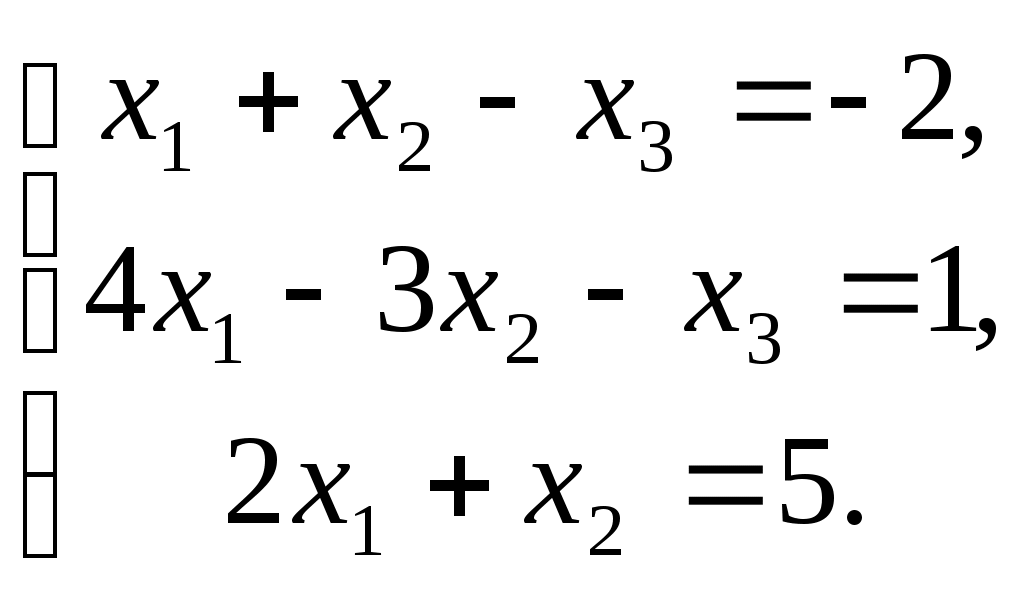 2. 2.  Вариант №5. Решить систему уравнений : 1. 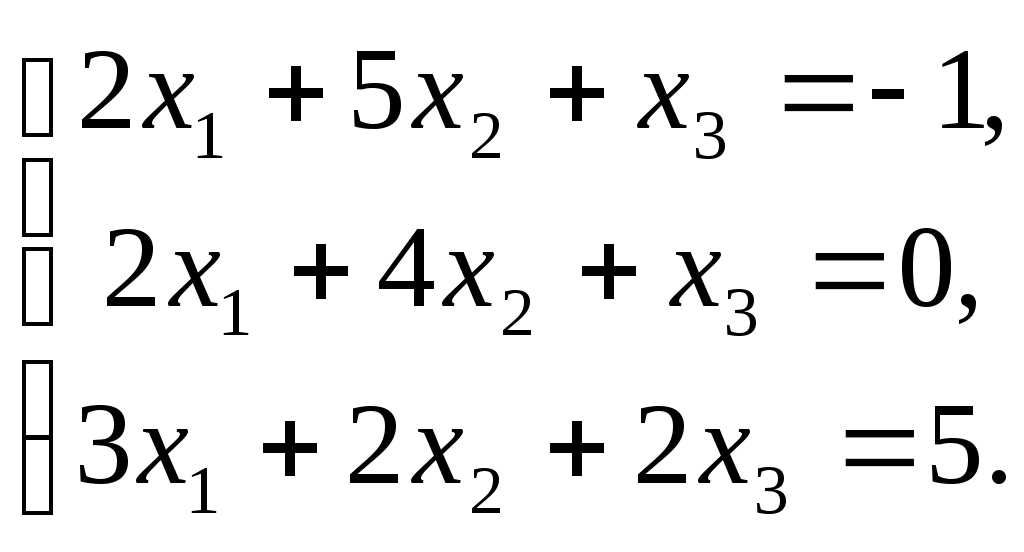 2. 2.  Вариант №6. Решить систему уравнений : 1.  2. 2. 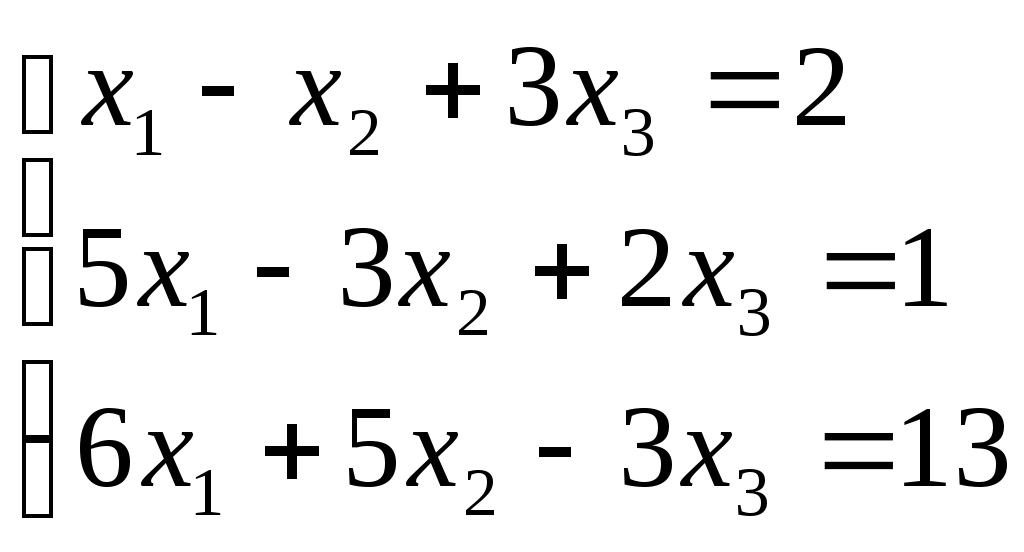 Вариант №7. Решить систему уравнений : 1. 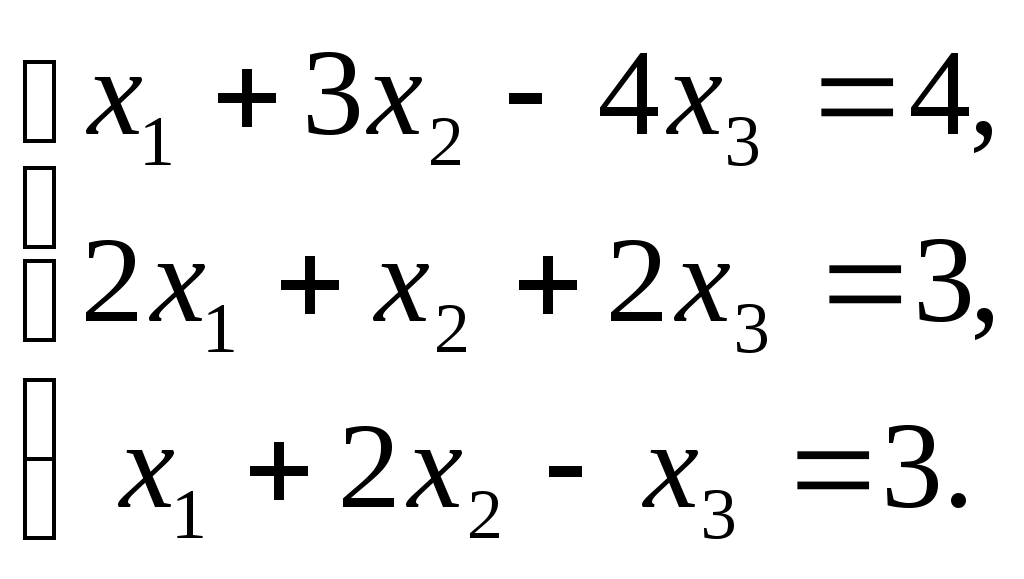 2. 2. 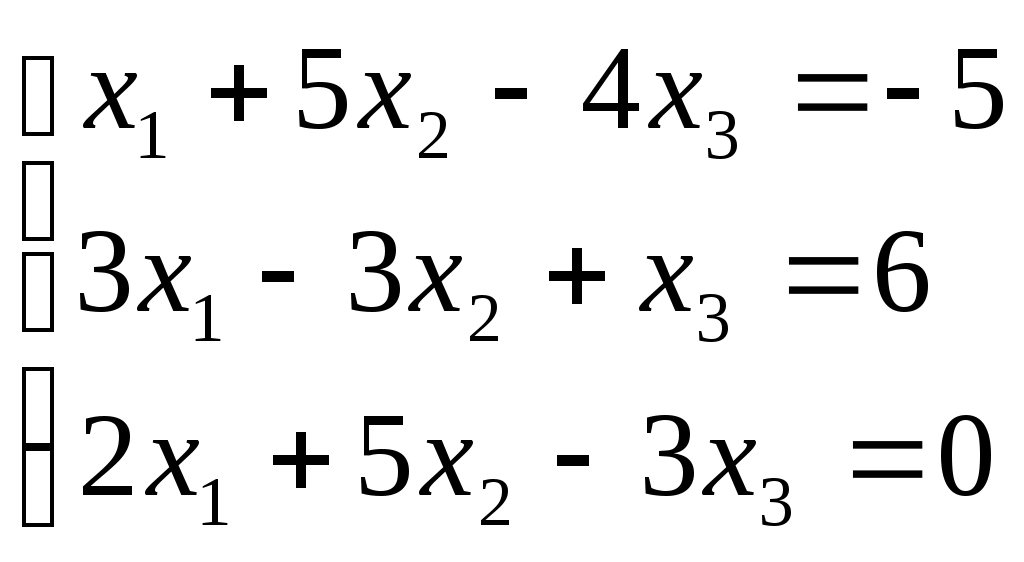 Вариант №8. Решить систему уравнений : 1. 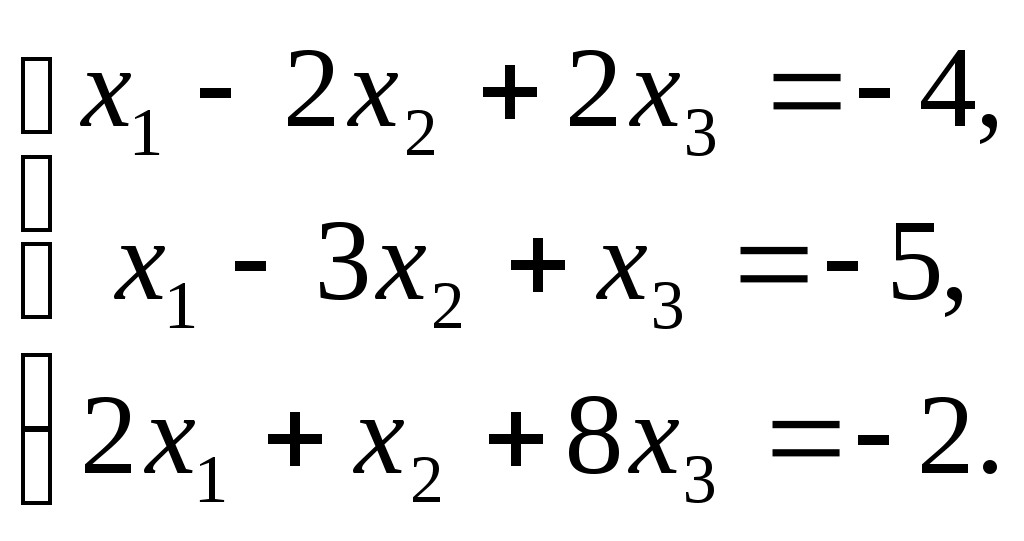 2. 2. 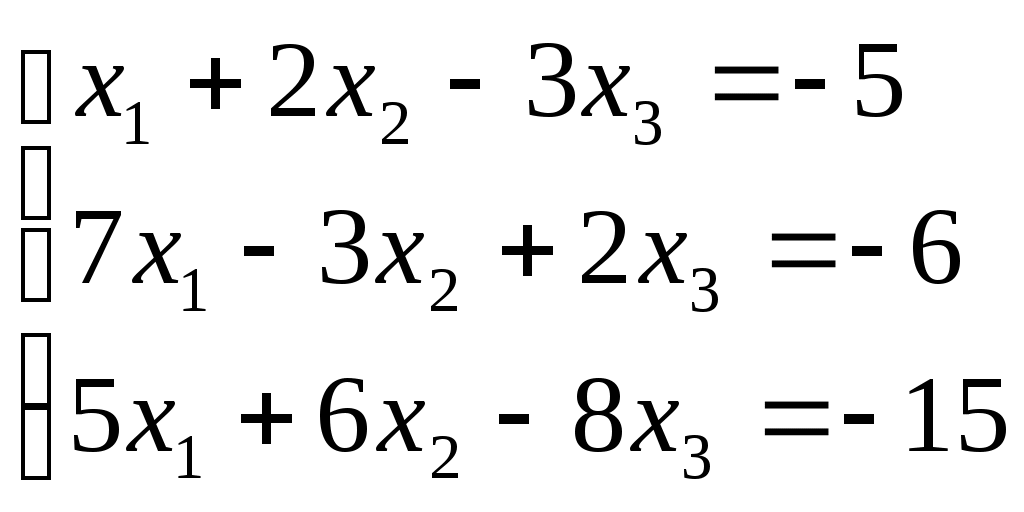 Вариант №9. Решить систему уравнений : 1. 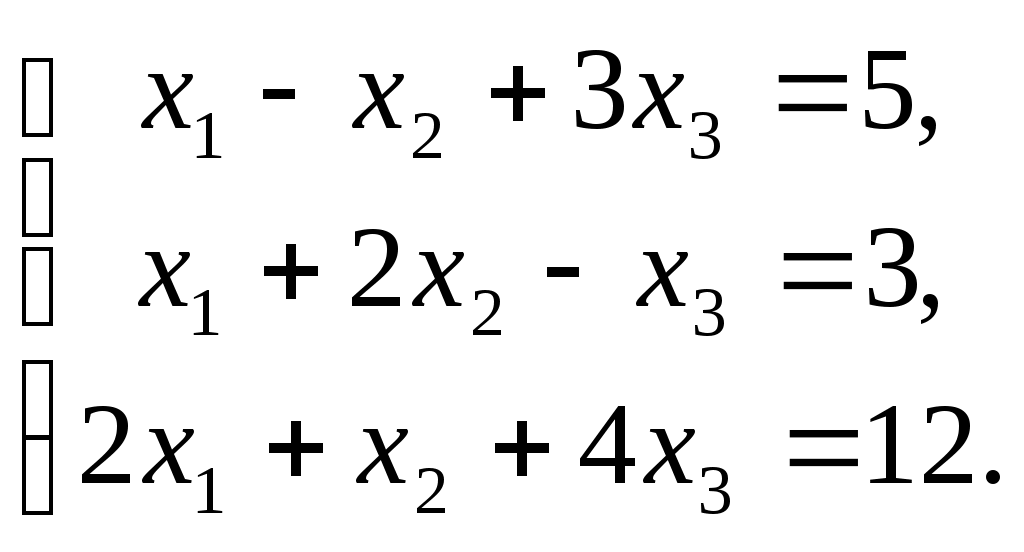 2. 2. 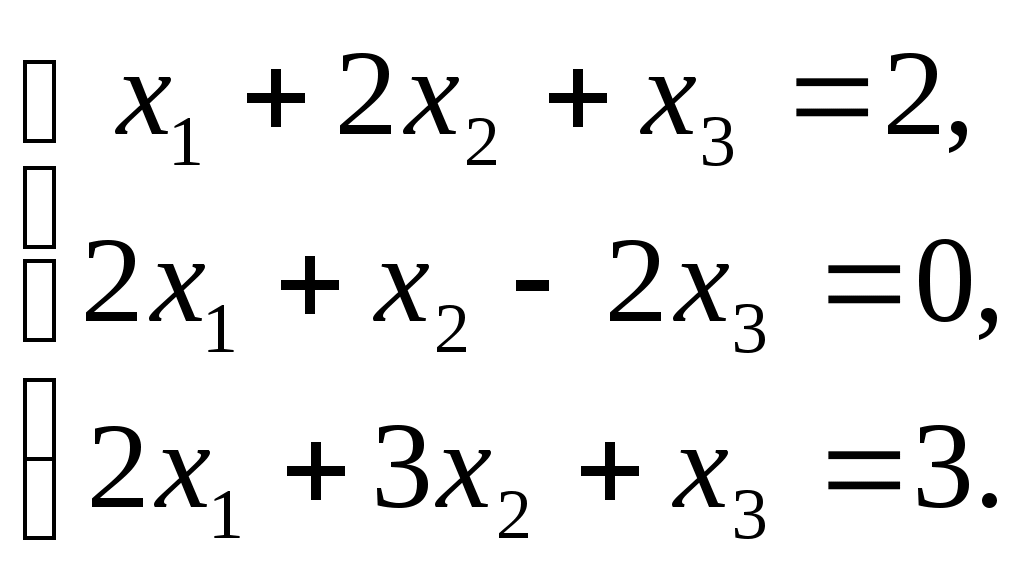 Вариант №10. Решить систему уравнений : 1. 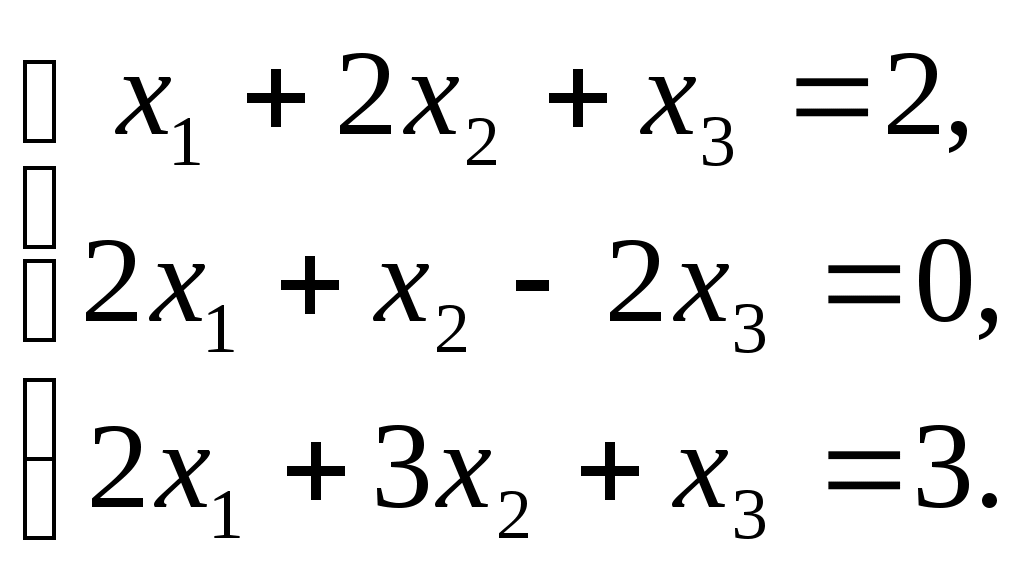 2. 2. 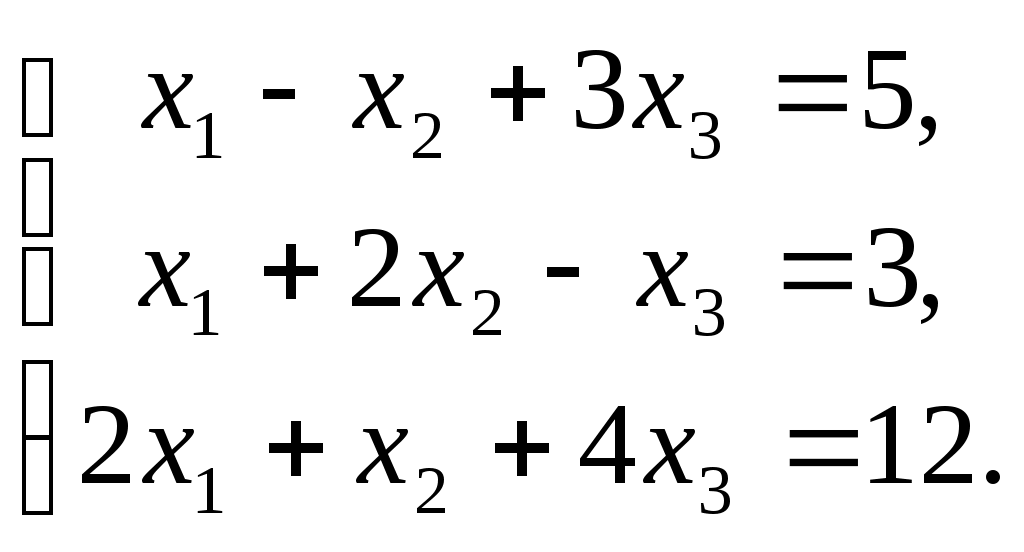 Вариант №11. Решить систему уравнений : 1. 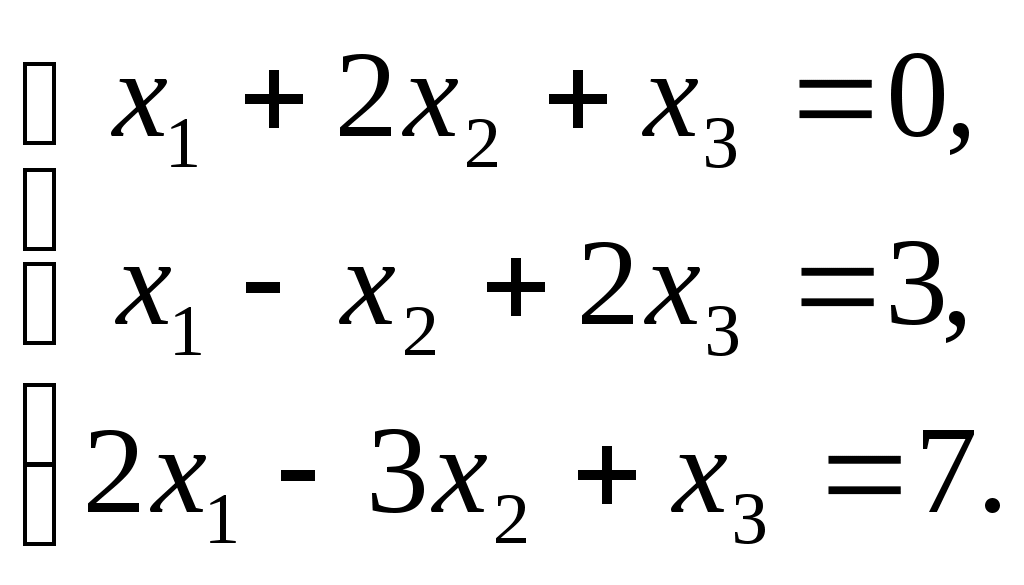 2. 2. 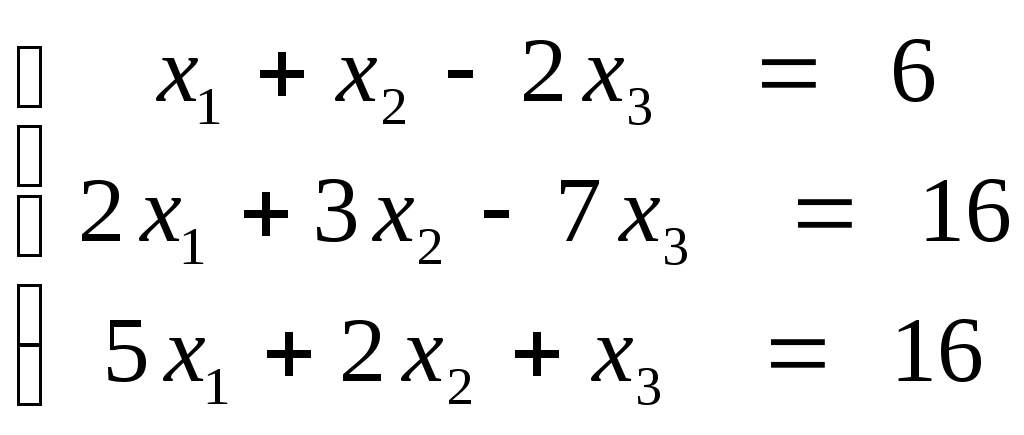 Вариант №12. Решить систему уравнений : 1. 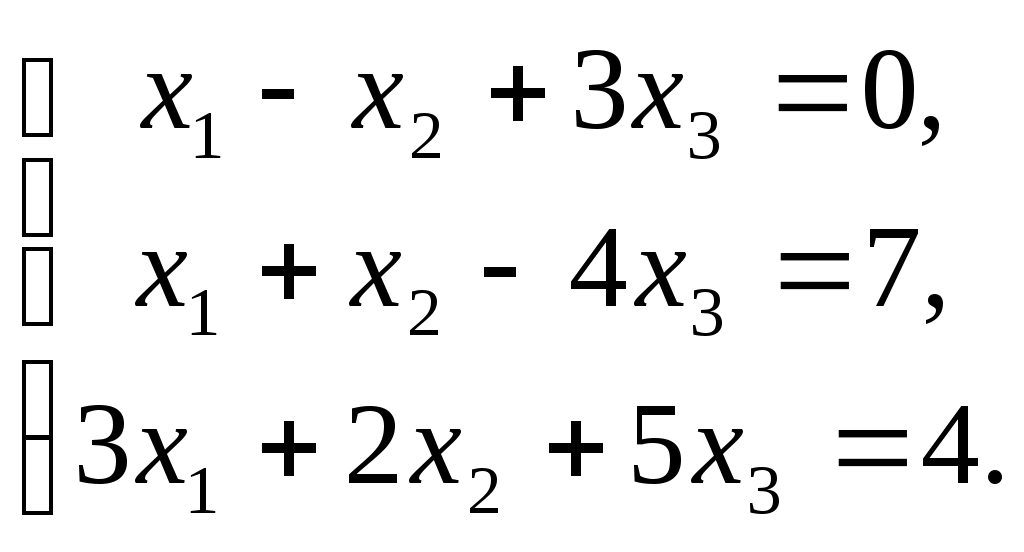 2. 2. 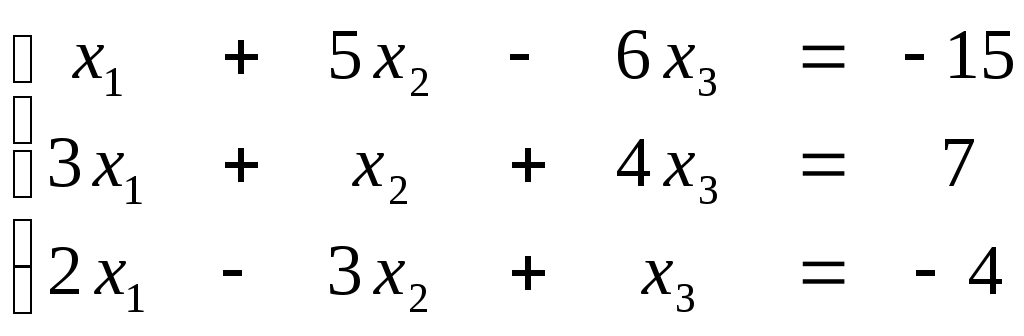 Вариант №13. Решить систему уравнений : 1. 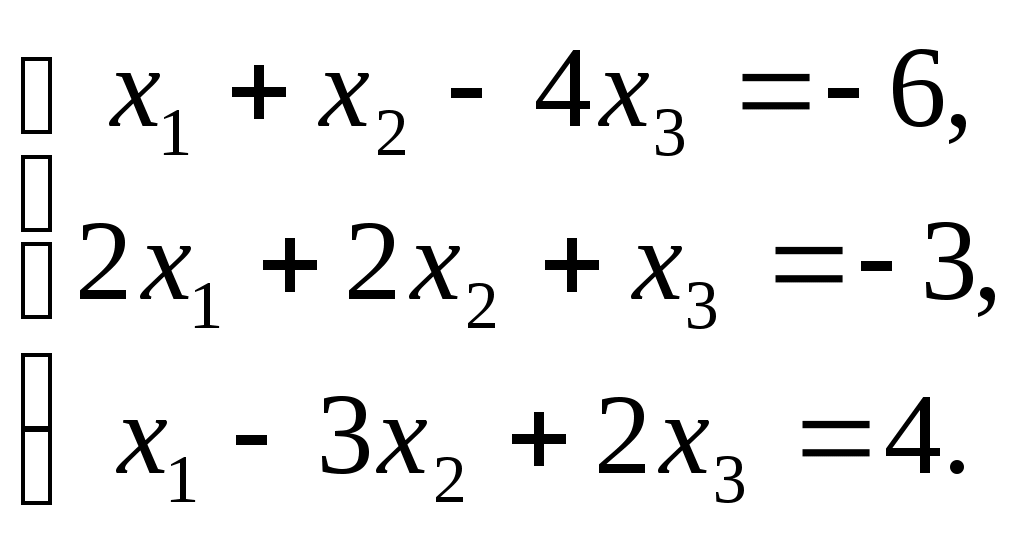 2. 2. 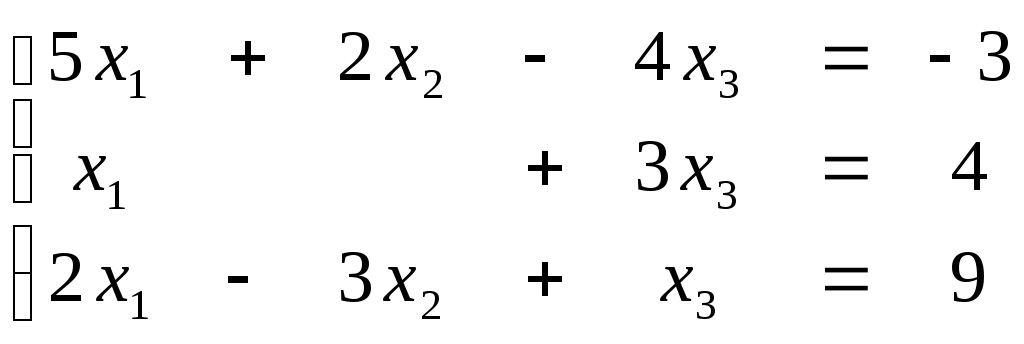 Вариант №14. Решить систему уравнений : 1. 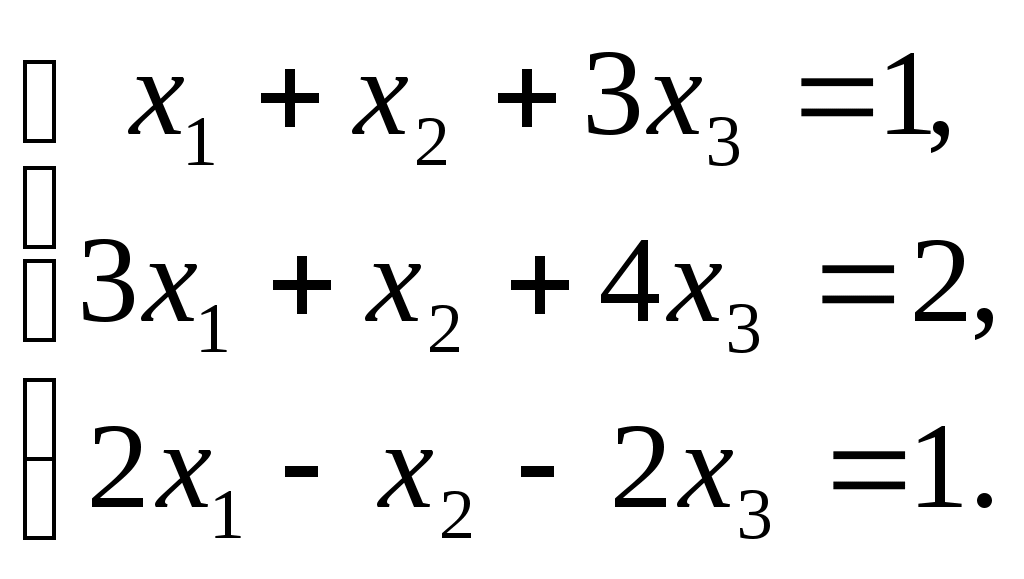 2. 2. 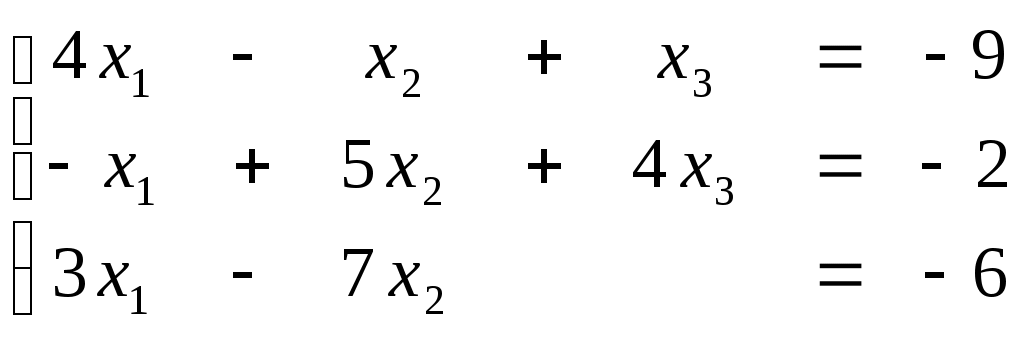 Вариант №15. Решить систему уравнений : 1. 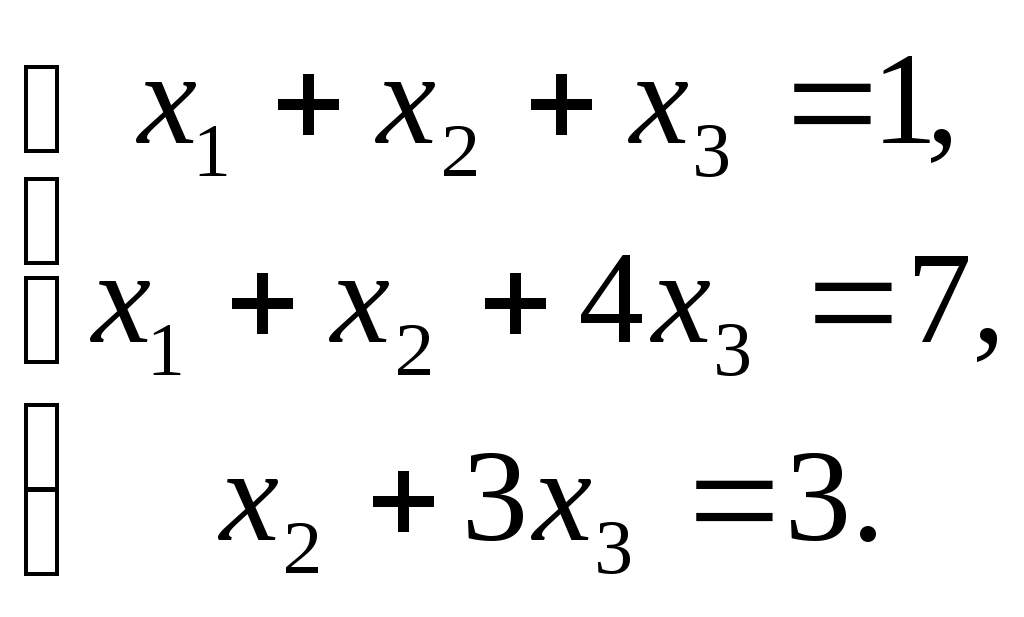 2. 2. 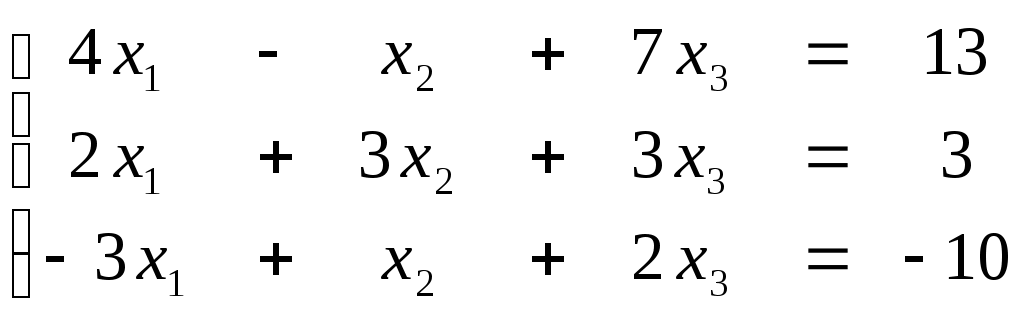 Вариант №16. Решите систему уравнений : 1. 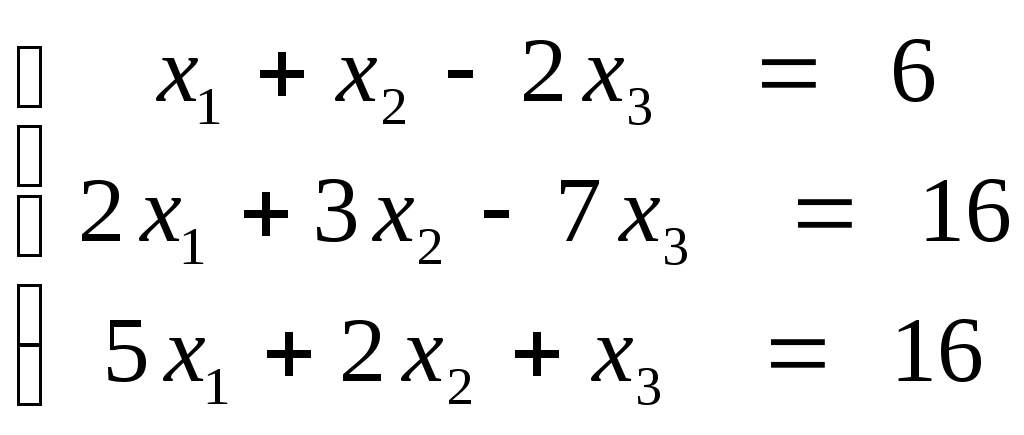 2. 2.  Вариант №17. Решите систему уравнений : 1. 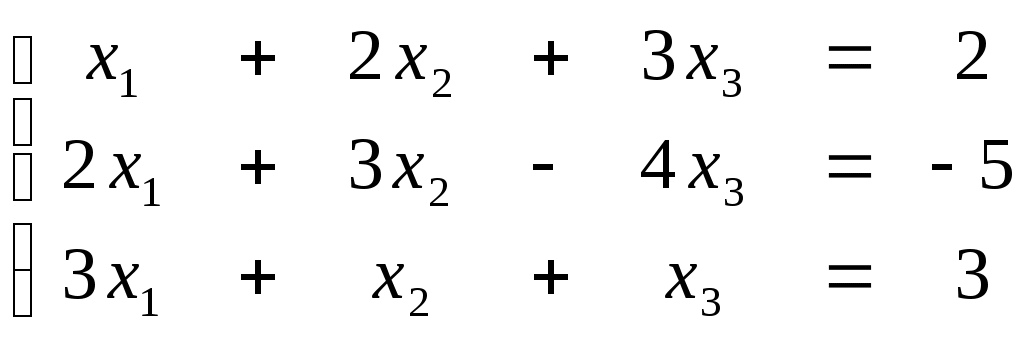 2. 2. 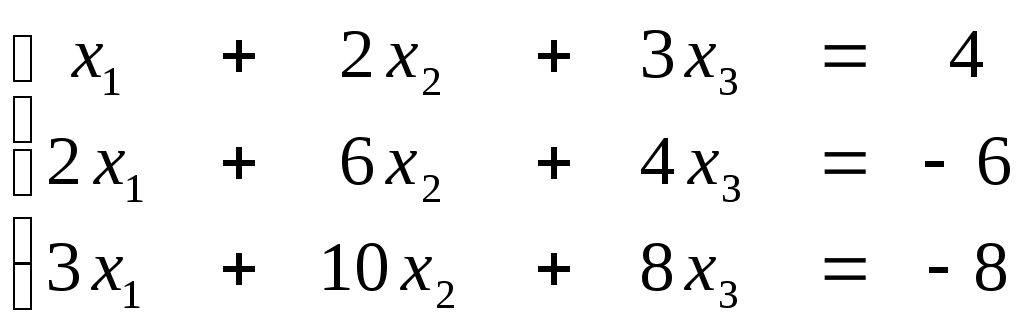 Вариант №18. Решите систему уравнений : 1. 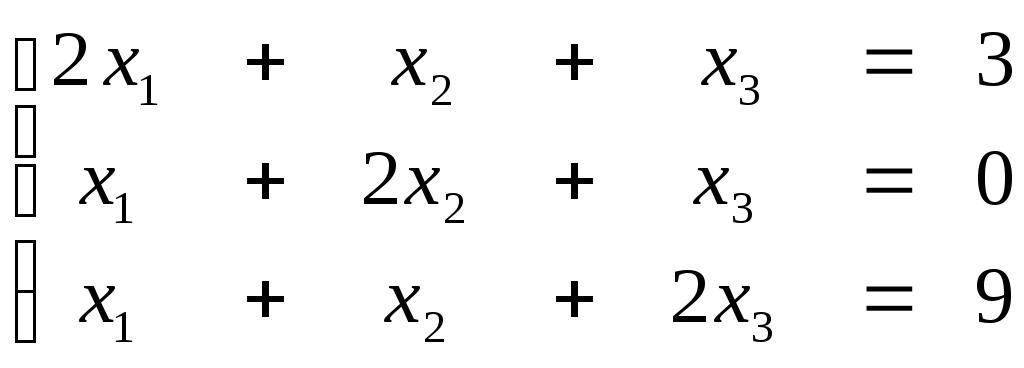 2. 2. 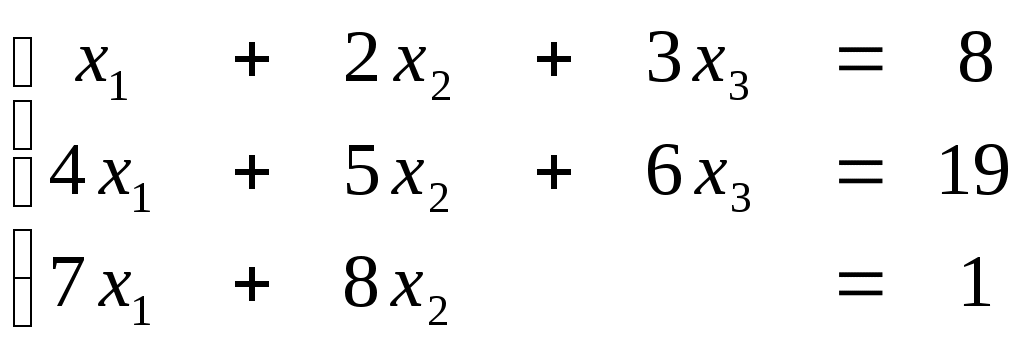 Вариант №19. Решите систему уравнений : 1. 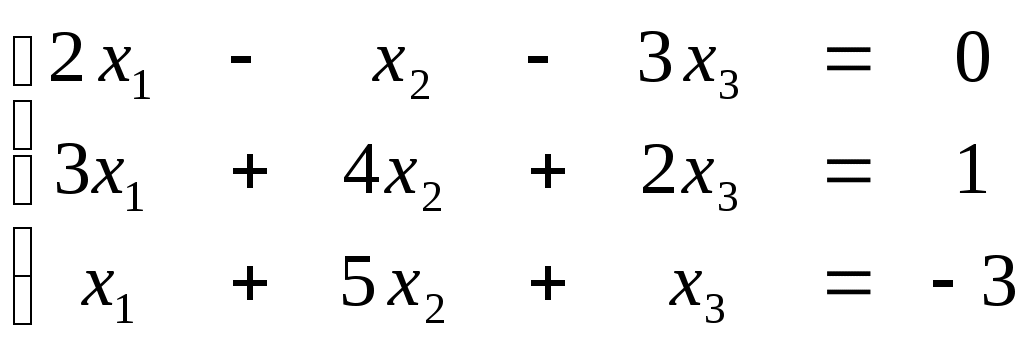 2. 2. 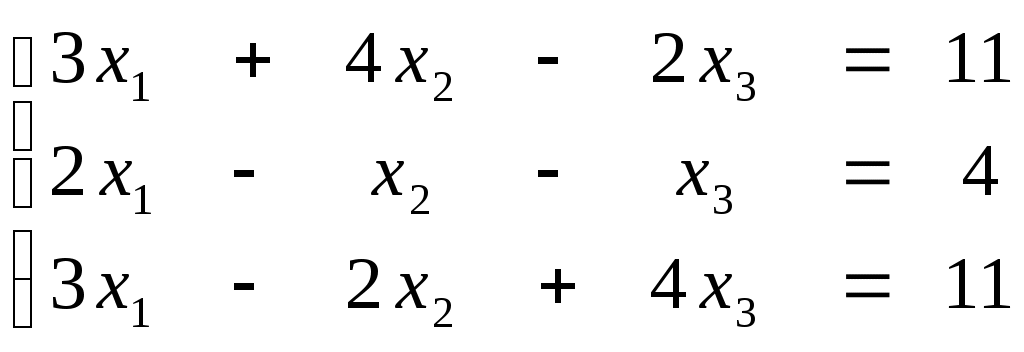 Вариант №20. Решите систему уравнений : 1. 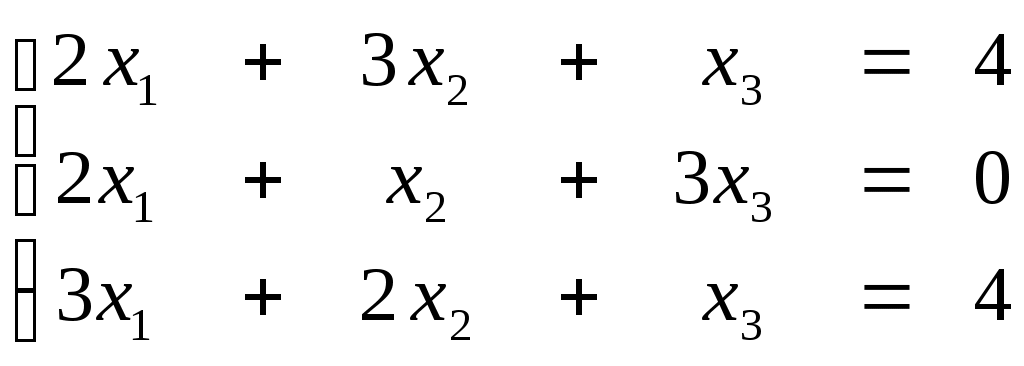 2. 2. 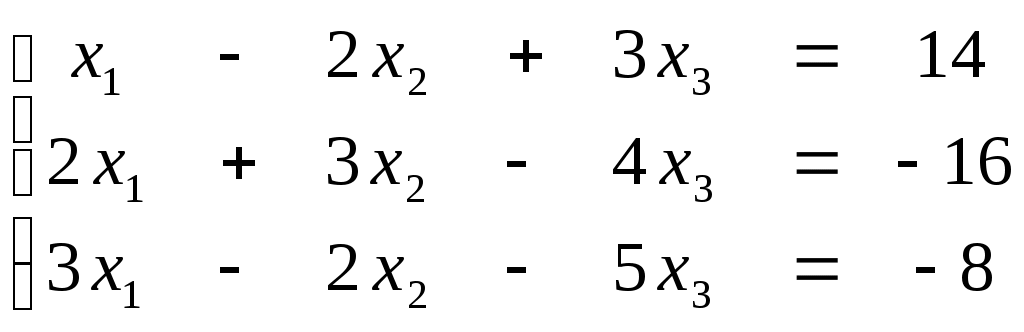 Вариант №21. Решите систему уравнений : 1.  2. 2. 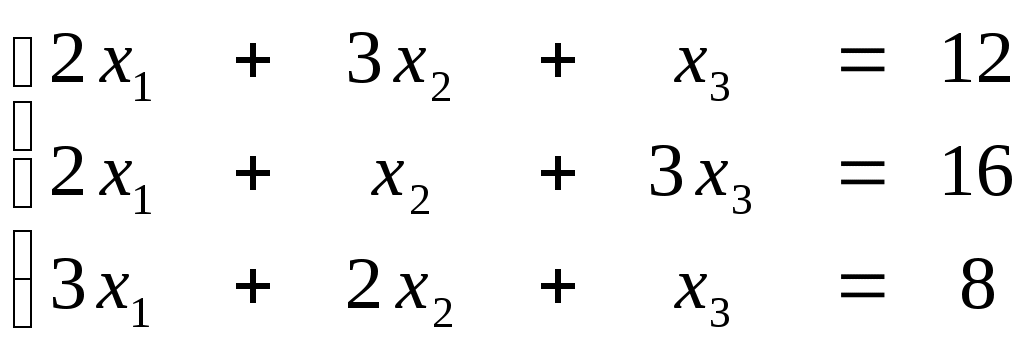 Вариант №22. Решите систему уравнений : 1. 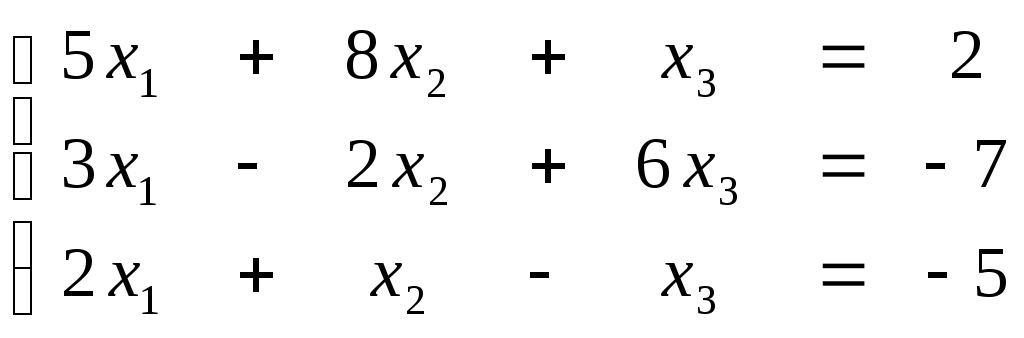 2. 2. 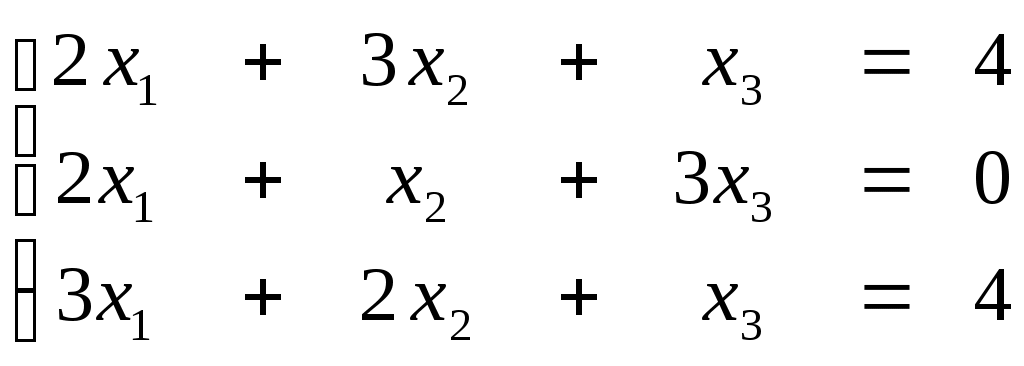 Вариант №23. Решите систему уравнений : 1. 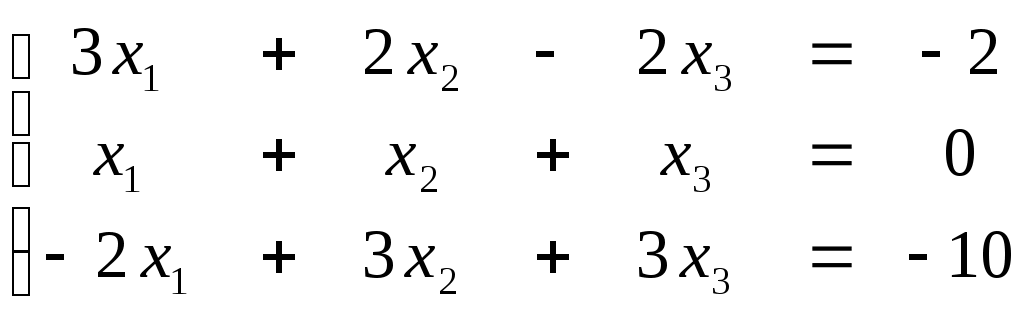 2. 2. 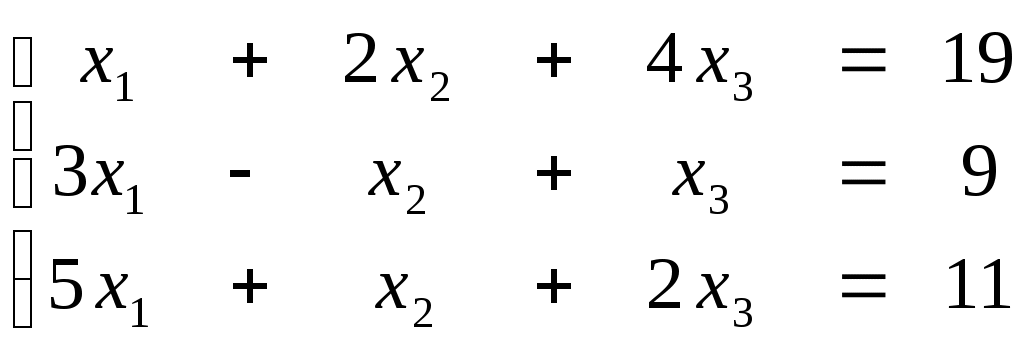 Вариант №24. Решите систему уравнений : 1. 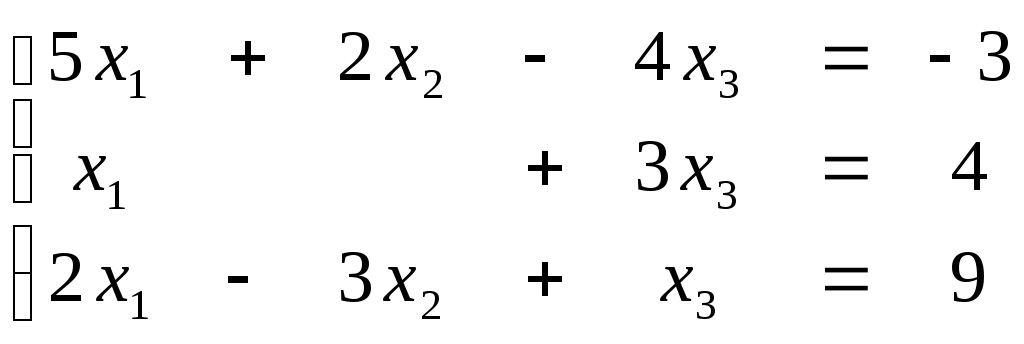 2. 2. 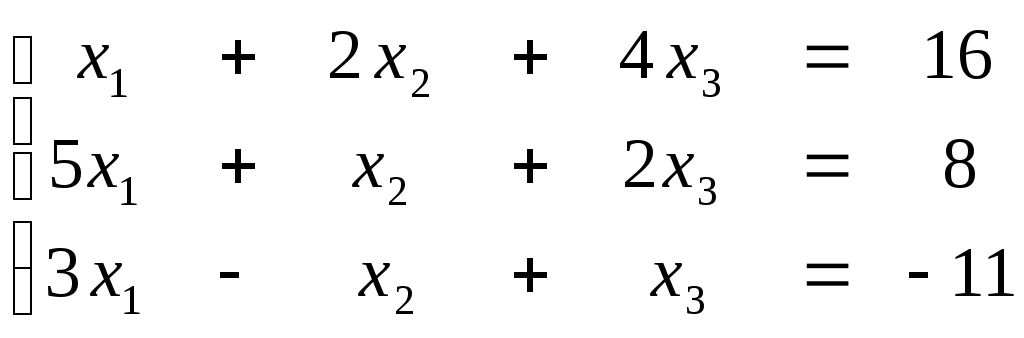 Вариант №25. Решите систему уравнений : 1. 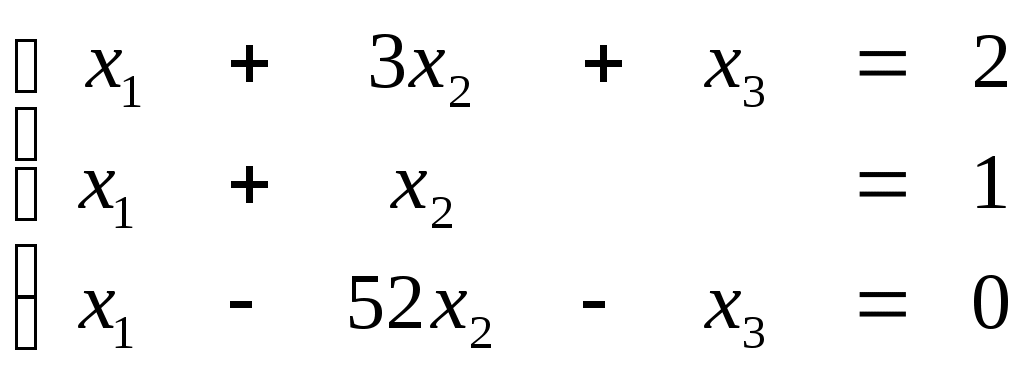 2. 2. 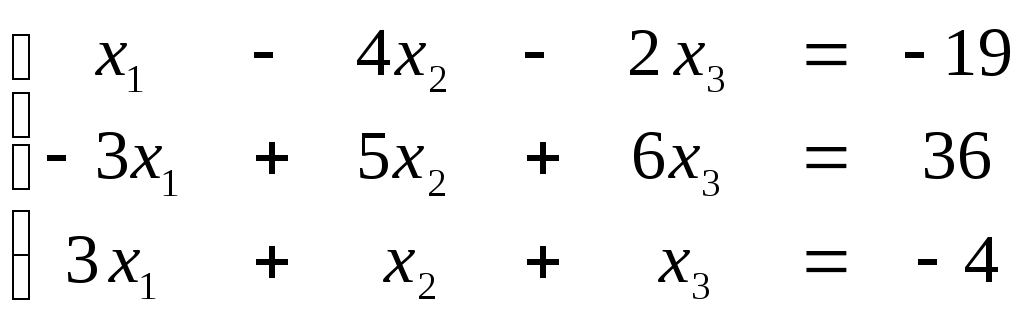 Вариант №26. Решите систему уравнений : 1. 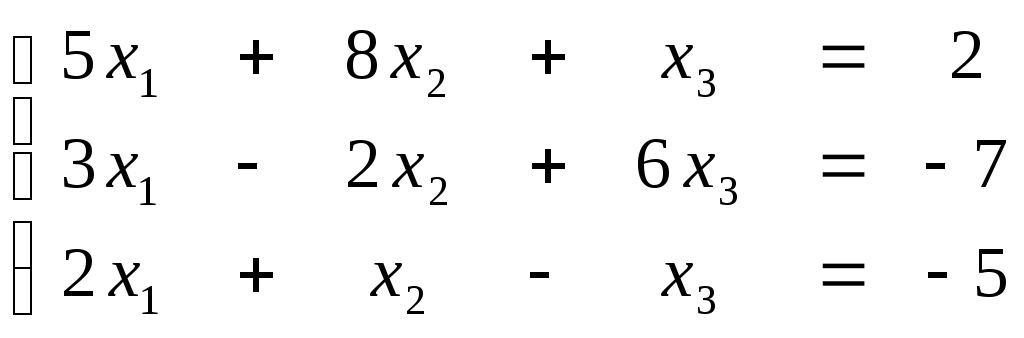 2. 2. 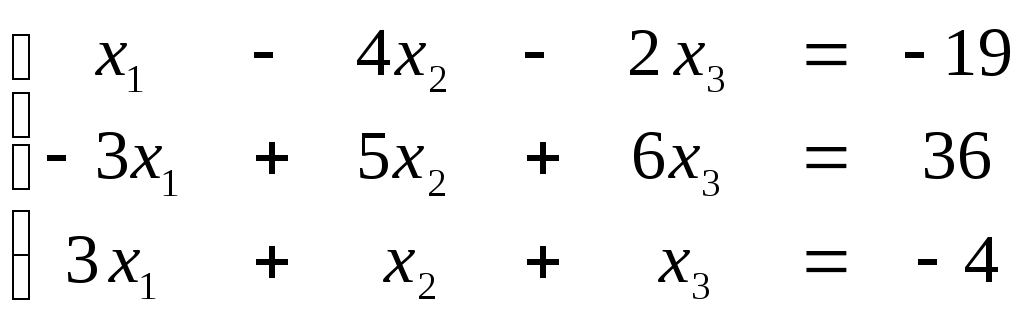 Вариант №27. Решите систему уравнений : 1. 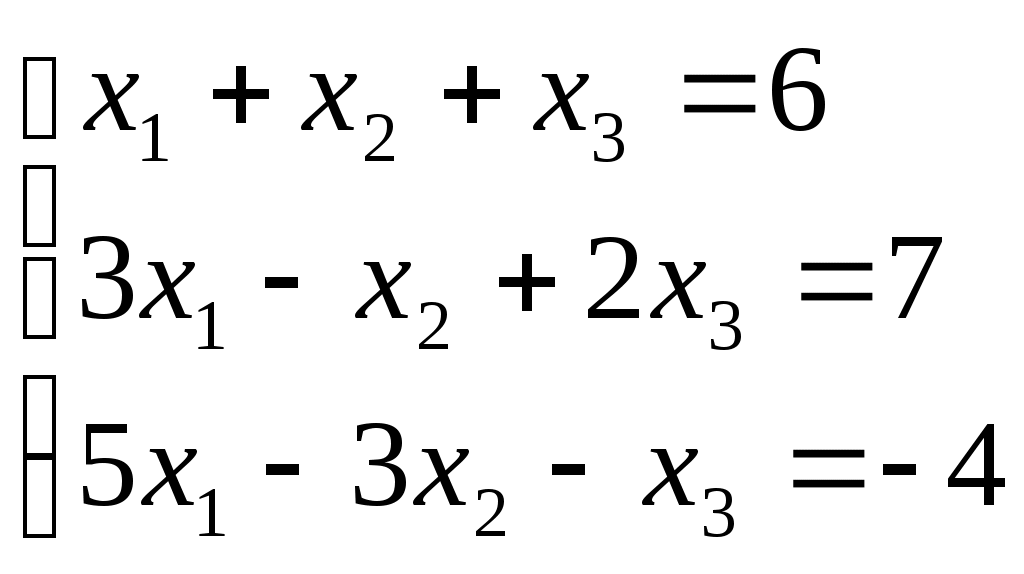 2. 2. 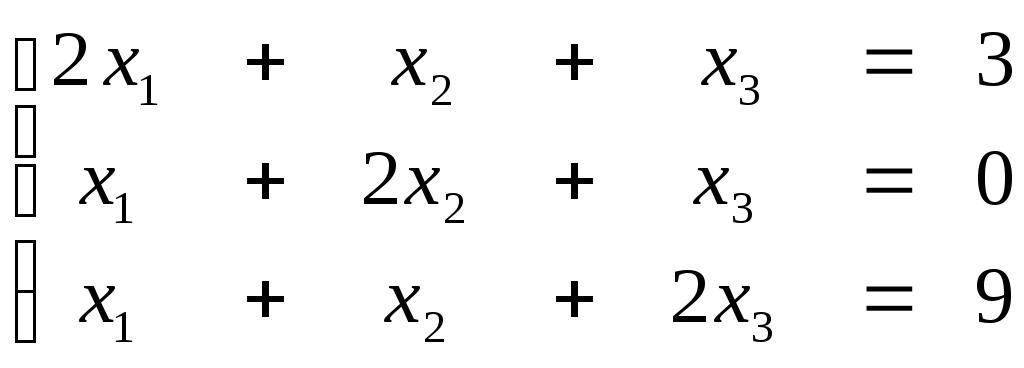 Вариант №28. Решите систему уравнений : 1. 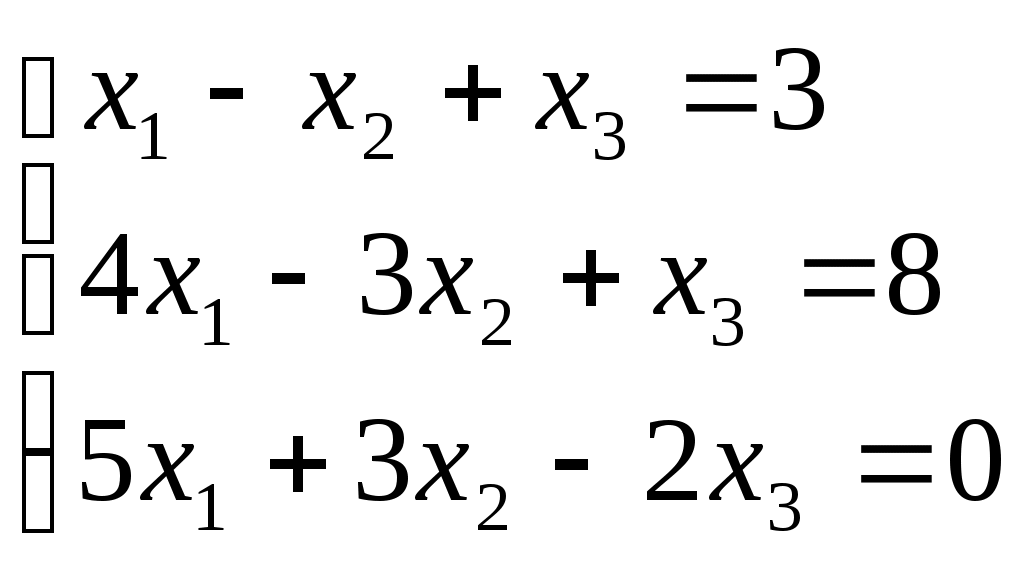 2. 2. 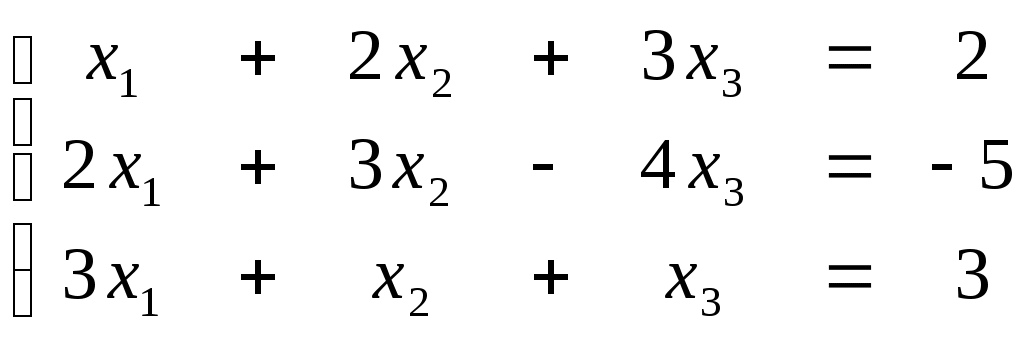 Вариант №29. Решите систему уравнений : 1. 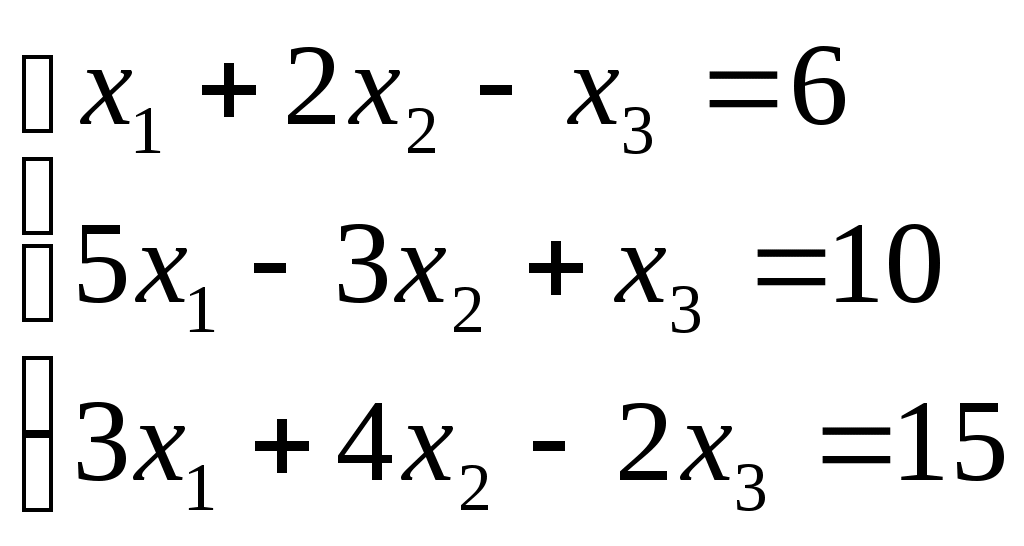 2. 2. 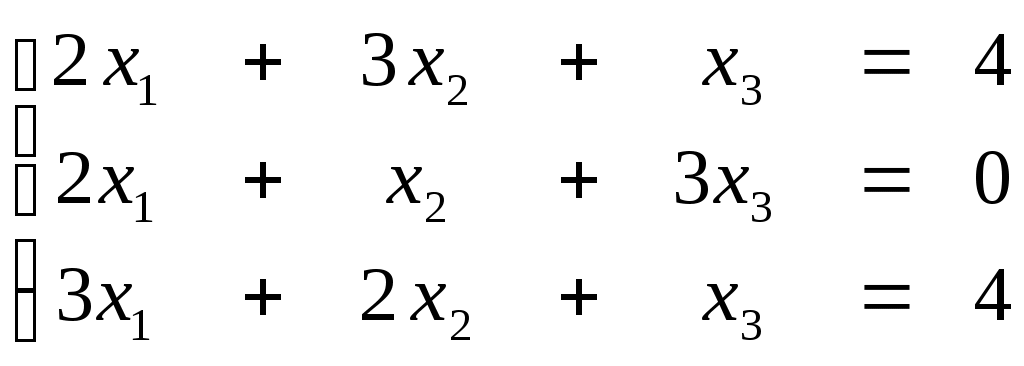 Вариант №30. Решите систему уравнений : 1.  2. 2. 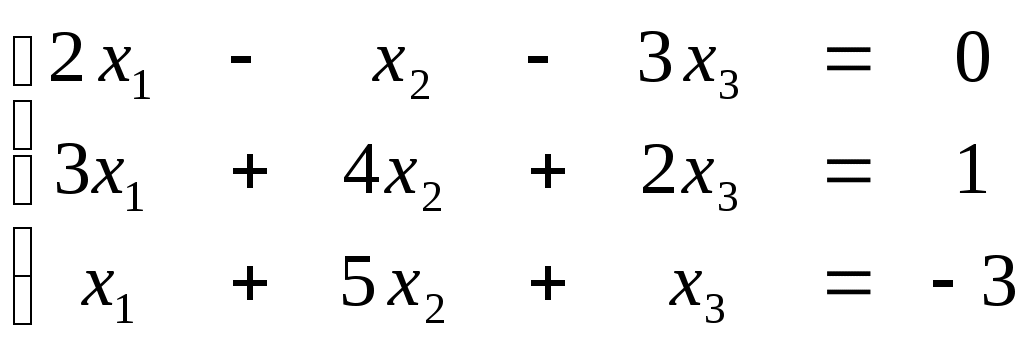 |
