1 Методи та механізми 2014. 1. 1 Основні послуги при застосуванні, уніфікація та стандартизація криптографічних перетворень
 Скачать 1.75 Mb. Скачать 1.75 Mb.
|
. Сутність і стан розробки алгоритму NTRU. В алгоритмі НШ NTRU всі операції здійснюються в фактор - кільці. Криптографічна стійкість алгоритму заснована на складності розв’язання задачі знаходження короткого вектора у заданій решітці. Показано, що крипто стійкість NTRU-167 (параметр N = 167) приблизно відповідає RSA-512, а стійкість NTRU-263 та NTRU-503 приблизно відповідає RSA-1024 та RSA-2048 відповідно. Основними складовими алгоритму крипто перетворення в фактор - кільці є вибір загально - системних параметрів, генерування асиметричних пар ключівПараметри алгоритму NTRU та ключі[ 217, 20-21]. Основні математичні поняття, що потрібні для розуміння алгоритму NTRU. Загальними параметрами алгоритму NTRU є: N – степінь фактор - кільця (усіченого кільця поліномів), причому елементи кільця подаються у вигляді поліномів степеня N – 1; модулі фактор - кільця - q та p, причому більший модуль – ціле число q, що використовується при обчисленні кільця поліномів. Модуль q не повинен мати спільних дільників з меншим модулем p. У якості загально - системних параметрів стандарту Х.9.98 q використовується степінь числа 2(211= 2048), а в якості другого модуля p=3. Параметр N використовується для визначення набору кільця поліномів, у якому виконуються криптографічні перетворення. Набор поліномів являє собою множину R усіх поліномів, степінь яких менше ніж N, яка позначається як R=Z [X]/(XN-1) (1.142) Кільце R (1.142) ще не є усіченим, усічення виникає при зведенні коефіцієнтів поліномів за модулем q. Тому результат обчислення для Z/q Z дає фактор - кільце, яке будемо позначати як Rq = (Z/ q Z) [X]/(XN- 1) (1.143 3.48) У таблиці 1.11 наведені параметри основного алгоритму разом з поясненням кожного з них [217]. У таблиці 1.12 наведені значення параметрів для різних рівнів безпеки, які рекомендує NTRU Cryptosystem. Алгоритм NTRU фактично носить імовірнісний характер, тобто існує невелика ймовірність помилки при розшифруванні. Але при відповідному виборі параметрів, імовірність помилки розшифрування може дорівнювати 10–25 або менше. Параметри, що рекомендовані NTRU Cryptosystem для використання в комерційних застосуваннях, наведені в таблиці 1.12. Таблиця 1.11 Загально - системні параметри та ключі NTRU
Таблиця 1.12 Рекомендованізначення розмірів параметрів для різних рівнів безпеки NTRU
Генерування асиметричних пар ключів[217,20-21]. Генерування асиметричної пари здійсню отримувач, наприклад абонент B. Він вибирає (генерує), згідно з вимогами табл. 1.11 два випадкових поліноми f і g, що визначені в кільці R. Причому поліноми f і g повинні мати мультиплікативно зворотні поліноми в кільці за модулем загальних параметрів р і q. Позначимо такі мультиплікативно зворотні значення для полінома f 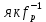 (F p)та (F p)та 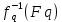 відповідно. Вони мають бути розраховані точно тільки для обраного f. відповідно. Вони мають бути розраховані точно тільки для обраного f.Особистий ключ fмає обчислюватись згідно з рекомендаціями [217] у кільці поліномів (Z/ q Z) [X]/(XN- 1) у вигляді f = (1 +pF) modq, (1.144) де р = 3 – загальний (доменний параметр), F – випадковий поліном, алгоритм генерування якого визначено в стандарті Х9.98. Далі Вобчислює свій відкритий ключ у вигляді многочлена h у кільці поліномів (Z/ q Z) [X]/(XN- 1) згідно з правилом: h =  * g) mod q, (1.145) * g) mod q, (1.145)де g випадково обраний, згідно з вимогами табл. 1.11 поліном у кільці Rq. Поліноми f і g, повинні мати конкретну кількість коефіцієнтів, 0, +1 і –1 згідно табл. 1.11. Особистий (таємний) ключ f разом із зворотними  Fp) та Fp) та 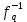 (Fq) єтаємними ключовими даними, а h – відкритим ключем. Значення N, p і q є параметрами алгоритму шифрування NTRU. Асиметричною парою ключів є (f, h) – пара особистого і відкритого ключів, що є поліномами степені N–1. (Fq) єтаємними ключовими даними, а h – відкритим ключем. Значення N, p і q є параметрами алгоритму шифрування NTRU. Асиметричною парою ключів є (f, h) – пара особистого і відкритого ключів, що є поліномами степені N–1.Алгоритм зашифрування[ ]. Нехайm повідомлення, яке потрібно зашифрувати. Воно подається у вигляді поліномів не вище N - 1 степені. Нехай абонент А бажає направлено зашифрувати для абонента В повідомлення m. Для цього А повинен знати справжні загальні параметри N, p і q та відкритий ключ абонента В – hb. Далі абонент А генерує «випадково» згідно з табл. 1.11 rа(ключ сеансу). Абонент А зашифрування виконує шляхом обчислення значення блоку - криптограми С c=(rа*hb + m) mod q (1.146) Алгоритм розшифрування[ 217 ]. При розшифруванні криптограми с абонент В повинен мати справжні загальні параметри N, p і q. Розшифрування здійснюється засобом згортки особистого ключа fbта криптограми с як поліномів N–1 степеня в кільці (Z/ q Z) [X]/(XN- 1) a= fb*с mod q. (1.147) Для отримання кандидата в розшифроване повідомлення m’ коефіцієнти полінома азводяться за модулем в інтервалі [А, А+q-1], а також по модулю. Попередні оцінки алгоритму НШ в фактор - кільці. Існує значне число крипто аналітичних атак вирішення задачі повного розкриття, основними з них можуть бути такі[ ]: атака з адаптивно підібраним текстом; атаки, що пов’язані з некоректним вибором загальних параметрів; атаки, що пов’язані з помилками при генеруванні ключів і параметрів; атаки, що пов’язані з використанням при криптоаналізі алгоритмі, що реалізуються на квантових комп’ютерах тощо. Одним з основних методів вирішення задачі повного розкриття є пошук найближчого вектору (найкоротшого) на основі зведення решітки метод LLL (Lenstra, Lenstra and Lovasz) [217, 65, 66]. Алгоритм дозволяє знайти достатньо невеликий вектор за поліноміальний час, але у загальному випадку алгоритм не дозволяє знайти найкоротший вектор. Існує багато удосконалень методу[66, 217]. Але складність цих методів для вирішення задачі пошуку найменшого вектора в загальних решітках є експоненційною. Складною також задачею є пошук найкоротшого вектора в решітці великого розміру. Нині найкращим із методів криптоаналізу фактор - кільця вважається метод LLL зведення в решітках. Для того щоб перевірити на практиці захищеність системи NTRUEncrypt за допомогою метода LLL було розв’язано багато задач знаходження найкоротшого вектора для решіток різних розмірностей. За результатами цих експериментів було отримано графічне представлення часу, потрібного для знаходження необхідного вектора для заданої решітки. У табл. 1.13 наведені оцінки часу криптоаналізу відносно NTRUEncrypt, RSA та EC-DSA криптосистем для різних рівнів безпеки [217]. Як основний критерій рівня безпеки використовується довжина ключа блокового симетричного шифру. Таблиця 1.13 - Оцінки часу криптоаналізу відносно NTRUEncrypt, RSA та EC-DSA криптосистем для різних рівнів безпеки
У табл. 1.14 наведені результати порівняння розмірів ключів для NTRU, RSA та еліптичних кривих (EC). Таблиця 1.14Порівняння розмірів ключів для NTRU та інших асиметричних алгоритмів
У табл. 1.14використано такі позначення: LPub – довжина відкритого ключа, в бітах; - LPri — довжина особистого ключа, в бітах. Наскільки це можливо, детальніше результати оцінки криптографічної стійкості алгоритму Х9.98 подані у розділі 6 цієї монографії. У підсумку необхідно відзначити, що метод, який лежить в основі NTRU, відомий і досліджується протягом 20 років, тобто він дійсно пройшов випробовування часом. У табл. 1.15 наведено результати оцінки швидкостей NTRU, RSA та EC на процесорі з частотою 2 ГГц. Таблиця1.15 Порівняння швидкостей NTRU, RSA та ЕС
Аналіз даних таблиці 1.15 дозволяє зробити висновок, що основною перевагою NTRU є суттєво підвищена, у порівнянні з RSA, DSA та EC, швидкодія НШ. 1.6.8 Асиметричне крипто перетворення на основі бінарного відображення точок еліптичних кривих Проблемність застосування асиметричних крипто перетворень. Серед методів НШ необхідно відзначити метод, що ґрунтується на парному відображенні (спарюванні) точок еліптичних кривих [20-21, 35, 15,]. Математичні питання бінарного відображення точок еліптичних кривих розглянуті [267,20-21, 46-47]. Коротко розглянемо проблемні питання криптографії, які стали передумовою появи методу криптографічного перетворення, що ґрунтується на парному відображенні точок еліптичних кривих. Стан і проблемні питання застосування симетричної та асиметричної криптографії. При застосуванні інфраструктури відкритих ключів (ІВК), що грунтується на сертифікатах відкритих ключів, обов’язковими складовими є такі[ 20-21 ]: - уповноважений на реєстрацію (УР); - уповноважений на сертифікацію (УС); - база сертифікатів (директорія); - сервіс анулювання та блокування (CRL) тощо. Практичне застосування ІВК та аналіз ряду джерел дозволили виділити відносно ІВК такі проблемні питання та протиріччя [22]: 1) значні матеріально технічні витрати на створення, впровадження, застосування та супроводження ІВК; 2) значна законодавча та нормативно-правова підтримка; 3) обов’язковість акредитації, експертизи, контролю та управління ІВК на державному рівні; 4)певною мірою психологічна неприйнятність ІВК, непрозорість тощо; 5) певна складність нарощування, об’єднання, розширення, модифікування ІВК тощо; 6) необхідність стандартизації та регламентації діяльності; 7) значна вартість обслуговування та надання послуг, тому така діяльність не завжди є комерційно вигідною тощо . Указані недоліки значною мірою можуть бути усунуті при застосуванні криптографії на ідентифікаторах, яка у свою чергу реалізується на основі застосування спарювання точок еліптичних кривих. Вступ в асиметричну криптографію на ідентифікаторахПо суті основним завданням асиметричної криптографії, що базується на ідентифікаторах, є виключення необхідності виготовлення й обслуговування сертифікатів відкритих ключів. Важливою перевагою такого підходу є можливість застосування замість відкритого ключа (сертифіката) особистої ідентифікаційної інформації. В якості ідентифікаційної інформації може бути адреса електронної пошти, ІР-адреса на мережному рівні тощо. Така адреса може бути подана у вигляді бінарного ідентифікатора ID 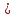 {1,0}. Обовязк4овим елементом такої системи є уповноважений на генерацію (УГ). Він повинен мати свій головний(майстер) ключ, що використовується для генерування особистих ключів користувачів. Але, так як особистий ключ має бути пересланий від УГ користувачеві, то усі користувачі повинні мати з УГ захищений канал зв’язку на індивідуальних ключах. Майстер-ключ УГ за важливістю є таким же, як і особистий ключ уповноваженого на сертифікацію ІВК (центра сертифікації). {1,0}. Обовязк4овим елементом такої системи є уповноважений на генерацію (УГ). Він повинен мати свій головний(майстер) ключ, що використовується для генерування особистих ключів користувачів. Але, так як особистий ключ має бути пересланий від УГ користувачеві, то усі користувачі повинні мати з УГ захищений канал зв’язку на індивідуальних ключах. Майстер-ключ УГ за важливістю є таким же, як і особистий ключ уповноваженого на сертифікацію ІВК (центра сертифікації). Аналіз показує, що відносно системи на базі ідентифікаторів обов’язковим є виконання таких вимог (Рис 1.13): користувач (відправник) А має бути повністю впевнений у правильності ідентифікатора того хто отримує, тобто сторони В; уповноважений на генерування повинен встановити (передати) особистий (таємний) ключ тільки стороні отримання В. 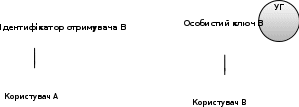 Рис. 1.13. Приклад функціонування асиметричної криптосистеми на ідентифікаторів Криптографія на базі ідентифікаторів головним чином заснована на криптографічному примітиві – бінарних відображеннях (спарюванні) точок на еліптичних кривих [20-21]. Математичні основи спарювання точок на еліптичних кривий були відомі ще з 1972 року. Бінарне відображення має дуже важливу властивість, яка має назву білінійність [14-16, 20-21 ]. Якраз на базі білінійності ґрунтується його нове криптографічне застосування. На практиці доведено, що застосування криптографії на ідентифікаторах дозволяє: 1) спростити ІВК за рахунок відмови від використання сертифікатів, так як немає необхідності в обслуговуванні, управлінні, створенні, видаленні та розподіленні сертифікатів 2) зменшити число складних компонентів (директорій) ІВК. 3) автоматично скасувати (анулювати) компрометовані ключі. Сутність методу НШ на ідентифікаторах. Одним з перших методів шифрування на базі ідентифікаторів запропонований у 2001 році авторами роботи [20-21] (Boneh-Franklin). Вказаний метод є реалізацією протоколу направленого шифрування на ідентифікаторах. Безпека протоколу шифрування базується на складності вирішенні білінійної проблеми Діффі-Геллмана (BDHP) [ 20-21, 46-47]. Направлене шифрування на ідентифікаторах. Ідея направленого шифрування базується на основній властивості скалярного відображення – його білінійності. Вона полягає в тому, що для деяких точок еліптичної кривої B і D, а також цілих чисел a та с, справедливим є співвідношення: 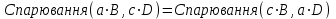 (1.148) (1.148)Для пояснення розглянемо, згідно з рис. 1.13 протокол направленого шифрування на ідентифікаторах з використання білінійного відображення точок еліптичних кривих. Нехай відправником є користувач А і він здійснює зашифрування для користувача В. Будемо вважати, що користувачі мають доступ до справжніх загальних параметрів, що ними використовуються. Реалізуючи зашифрування, зробимо спробу повторити протокол направленого шифрування. Спочатку користувач А генерує випадкове число r і, знаючи загальну для користувачів базову точку G на еліптичній кривій, обчислює відкритий ключ сеансу: 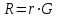 . (1.149) . (1.149)Випадкове число r по суті є особистим (таємним) ключем сеансу, воно має вибиратись із умови 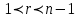 , де n – порядок базової точки. У результаті виконання обчислень згідно (1.149) одержується значення точки R на еліптичній кривій - відкритий ключ сеансу , де n – порядок базової точки. У результаті виконання обчислень згідно (1.149) одержується значення точки R на еліптичній кривій - відкритий ключ сеансуДалі користувач А має виробити ключ зашифрування, використовуючи властивість бінарного відображення (1.148). Для цього він вибирає для (1.148)такі параметри: а=r, B=IDb, c=s, D=G(1.150) а також обчислює таємний ключ сеансу для направленого зашифрування  , (1.151) , (1.151) причому 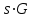 в інфраструктурі він отримує як загальний параметр. в інфраструктурі він отримує як загальний параметр.За умови узгодження між користувачами алгоритму симетричного шифрування (зашифрування, розшифрування) повідомлення М користувач А може здійснити використовуючи таємне значення k. Значення k у явному вигляді використовувати не можна. Тому необхідно використати відповідним чином узгоджену функцію вироблення ключа (ФВК) [ 20-21,202], наприклад, функцію гешування. За вказаних умов таємний ключ сеансу Кс симетричного шифрування виробляється як К с=ФВК(k) (1.152) На останок користувач здійснює зашифрування повідомлення М та отримує криптограму: C = E (Kc, M), (1.153) яку разом з відкритим ключем сеансу R передає користувачеві В. Направлене розшифрування на ідентифікаторах. Розшифрування криптограми C здійснюється користувачем В. Для цього користувач В робить запит УГ та отримує від нього по захищеному каналу особистий ключ розшифрування s. Використовуючи цей ключ, користувач В обчислює параметр спарювання k за правилом  , (1.154) , (1.154)а потім обчислює таємний ключ сеансу Кс згідно (1.152). На останок використовуючи узгоджений алгоритм розшифрування D, користувач В здійснює розшифрування криптограми і отримує відкрите повідомлення: M= D (Kc, C) (1.155) Наведений алгоритм шифрування забезпечує такі переваги: - забезпечується направлене зашифрування на отримувача; - при застосуванні симетричного крипто перетворення забезпечується середня або висока швидкодія шифрування; - немає необхідності використовувати систему ІВК/ Проблемними питаннями застосування крипто перетворень на ідентифікаторах є: необхідність довіри УГ; необхідність конфіденційного каналу зв’язку абонентів з УГ. Більш детальний аналіз крипто перетворень на ідентифікаторах наведено в 6 розділі. Викладений вище матеріал носить допоміжний характер і призначений для початкового ознайомлення. 1.7 Сутність, вимоги, класифікація та стандартизація криптосистем типу ЦП | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
