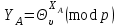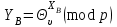1 Методи та механізми 2014. 1. 1 Основні послуги при застосуванні, уніфікація та стандартизація криптографічних перетворень
 Скачать 1.75 Mb. Скачать 1.75 Mb.
|
Таблиця 1.7 Алгоритми і параметри NTRU, що рекомендуються
1.6.3 Етапи створення та стандартизації криптоперетворень направленого шифрування Першою у 80-ті роки минулого була побудована та знайшло застосування асиметричне крипто перетворення у вигляді криптосистеми з відкритими ключами, що нині відома як RSA [149, 389, 2--23] система. Розробниками RSA системи вважають Рона Рівеста, Аді Шаміра і Леонарда Адлемана. Але у підручнику «Фізика квантової інформації» авторів Д. Бауместер, А. Екерт, А. Цайлингер на с. 37–38 [8] стверджується, що в Англії RSA-подібний алгоритм було винайдено на декілька років раніше. Основною особливістю RSA криптосистеми є її асиметричність, коли ключ зашифрування Кз не співпадає з ключем розшифрування Кр, тобто виконується вимога (1.116) у вигляді [ 20-23 ]: 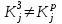 , (1.117) , (1.117)а знайти один ключ при відомому другому для відповідних значень загальносистемних параметрів можна не нижче ніж з субекспоненційною складністю. Хоч на сьогодні RSA криптосистема піддається нападам і щодо неї робляться різні прогнози, але вона проіснувала майже 35 років і дозволяє реалізувати НШ. Система RSA дозволяє якісно реалізувати криптографічними методами таку основну функцію, як неспростовність отримувача, а також відправника.. При чому, причетність отримувача може бути забезпечена за рахунок здійснення НШ з використанням відкритого ключа отримувача, а розшифрування засобом використання особистого (таємного) ключа отримувача. Основною вимогою до асиметричних криптосистем є забезпечення стійкості від існуючих атак. Але при аналізі першою вимогою ставиться забезпечення стійкості від атаки повне розкриття, коли при успішному її здійсненні криптоаналітик узнає(компрометує) особистий ключ власника. Для порівняльного аналізу в таблиці 1.8 та 1.9 наведено результати практичних досягнень в області криптоаналізу методом повного розкриття існуючих асиметричних криптосистем із зазначенням довжини ключа, часу, який був витрачений на здійснення криптоаналізу, та року, коли було здійснено криптоаналіз. Одиницею виміру є тимчасова складність в MIPS-Year та просторова складність у вигляді обсягу пам’яті, що була використана в процесі здійснення криптоаналізу [21-23]. Одиницею виміру є тимчасова складність в MIPS-Year та просторова складність у вигляді обсягу пам’яті, що була використана в процесі здійснення криптоаналізу. Таблиця 1.8 - Стан розв’язування задач факторизації RSA модуля N
Таблиця 1.9 - Досягнення у здійсненні криптоаналізу відносно асиметричних криптосистем
Дані, що наведені в табл. 1.9 підтверджують, що асиметричні крипто перетворення скоріше є ймовірно стійкими. Це пояснюється тим, що розвиток спеціальних розділів математики та збільшення потужності крипто аналітичних систем дозволяють компрометувати їх з часом. Як правило, виходом із такої ситуації є збільшення розмірів загальних параметрів і ключів або заміна більш стійкими крипто перетвореннями [20-23, 119, 121]. У цілому наведені в таблиці 1.9 дані відображають етапи створення та розвитку асиметричних криптосистем. Детально ці питання розглядаються в 6 розділі цієї монографії. На рис. 1.12 наведено повний перелік та деякою мірою класифікація асиметричних криптосистем, стійкість яких ґрунтується на складності розв’язання теоретико - числових задач [6,7,17, 21-23]      Рис. 1.12 Класифікація асиметричних криптосистем, стійкість яких ґрунтується на складності розв’язання теоретико - числових задач. У цілому наведені в таблиці 1.9 дані відображають етапи створення та розвитку асиметричних криптосистем. Детально ці питання розглядаються в 6 розділі. Особливістю криптоперетворень типу НШ є такі: пряме криптографічне перетворення виконується з використанням відкритого ключа 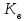 ; ;зворотне криптографічне перетворення виконується з використанням особистого ключа 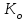 ; ;ключова пара (Ко, Кв) має бути випадковою та вибиратись із повної множини дозволених для використання ключових пар, причому 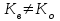 (1. 127) (1. 127)Відомий ряд методів побудування криптографічних систем направленого шифрування. Основними з них, на наш погляд, є такі: 1) Метод складання рюкзака [20-21]. Необхідно вкласти в рюкзак предмети з різною вагою, але щоб вага рюкзака залишалася постійною. Це нестійка система. 2) У 1978 р. була опублікована стаття, у якій був запропонований алгоритм RSA направленого шифрування. Він закріплений у міжнародному стандарті ISO 11166-1, 2. Окрім того, в США він закріплений у стандарті ANSI Х9.31. 3) У 1985 р. Ель-Гамаль запропонував новий механізм НШ в скінченному полі. В подальшому алгоритм, що є основою механізму, був досліджений та знайшов реалізацію, а а також запатентовані. На сьогодні рекомендовано до застосування стандарти Х9.30 та в міжнародних стандартах ISO/IEC 11770-3. 4) У подальшому були запропоновані й досліджені НШ за методом Ель - Гамаля в групі точок еліптичних. Вони знайшли реалізацію в ДСТУ ISO/IEC 15946-3 у вигляді механізмів та криптографічних протоколів, в тому числі НШ. Також тозроблені механізми та протоколи НШ в групі точок гіпер еліптичних кривих та на основі спарювання точок еліптичних кривих [20-21, 228,] тощо. 5) У квітні 2011 року Американським комітетом (Accredited Standards Committee) X9 NTRU (NTRUEncrypt) був затверджений у вигляді стандарту ANSI X9.98 [217], що грунтується на перетвореннях в фактор - кільці. Як показав аналіз NTRUEncrypt є найшвидшим алгоритмом асиметричного шифрування, він забезпечує в певних умовах швидкодію на два - три порядки вище, ніж RSA та при використанні перетворень в скінченних полях і групі точок еліптичних кривих. За надійністю та принципом дії алгоритм схожий з RSA, проте набагато простіший і не вимагає великих обчислювальних потужностей. Але головним є те, що він є стійким проти існуючих крипто аналітичних, наприклад складність атаки повного розкриття носить експоненційний характер[20-21, 217]. Таким чином, алгоритм NTRU, що поданий у стандарті США Х9.98, є досить перспективним, але вимагає, на наш погляд, подальших досліджень. Проведемо аналіз названих криптоперетворень НШ на предмет їх порівняння та обґрунтування перспективних. 1.6.4 Сутність та аналіз крипто перетворення в кільці. Алгоритм направленого шифрування. Крипто перетворення в кільці (RSA криптоалгоритм) є блоковим, у ньому повідомлення М розбивається на блоки Мi з довжиною блоку 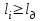 (2048 бітів мінімум), а згідно вимог [ 20-21,222] 2048, 3072 і більше бітів. Направлене зашифрування здійснюється поблочно , причому блок - криптограма обчислюється у вигляді (2048 бітів мінімум), а згідно вимог [ 20-21,222] 2048, 3072 і більше бітів. Направлене зашифрування здійснюється поблочно , причому блок - криптограма обчислюється у вигляді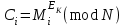 , (1.128) , (1.128)де 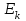 – є відкритий ключ прямого перетворення, N – модуль перетворення, причому – є відкритий ключ прямого перетворення, N – модуль перетворення, причому 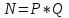 , (1.129) , (1.129)де у свою чергу P, Q – великі прості сильні числа[ ]. Розшифрування блока криптограми здійснюється за правилом: 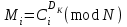 , (1. 130) , (1. 130)де Dк – є особистий ключ розшифрування. Асиметрична ключова пара 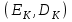 пов’язана між собою рівнянням: пов’язана між собою рівнянням: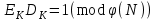 , (1.131) , (1.131)де 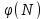 є функцією Ойлера від модуля N: є функцією Ойлера від модуля N: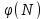 = = 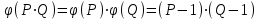 . .Якщо порівняння (1.131) має єдиний розв’язок, тобто існує єдина пара 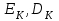 , то такий шифр є однозначним і за таких умов RSA криптосистема забезпечує однозначне направлене шифрування. , то такий шифр є однозначним і за таких умов RSA криптосистема забезпечує однозначне направлене шифрування.Система RSA належить до криптосистем з відкритими ключами. У цій системі ключі ЕkDk, причому один з них має бути особистим, а другий – відкритим. Наприклад, Еk – особистий, а Dk – відкритий, якщо вони використовуються для ЕЦП, і навпаки – якщо використовуються для направленого шифрування. Усі параметри (N, P, Q) також поділяються на два класи: N – відкритий, P, Q – конфіденційні (секретні). Сутність забезпечення моделі взаємної недовіри полягае в тому, що кожен користувач генерує ключі сам собі. Особистий ключ він залишає в себе і забезпечує його сувору конфіденційність. Відкритий ключ розсилає всім користувачам, з якими він позв’язаний. Користувач також забезпечує цілісність і дійсність відкритих ключів. Еk, Dk мають вибиратися з повної множини випадково, порівняно ймовір- но і незалежно, мають забезпечувати однозначну оборотність прямого і зворотного перетворення Попередня оцінка стійкості. У системі RSA криптоаналіз, метою якого є визначення особистого (таємного) ключа, наприклад, Ек ключа ключової пари ( 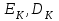 ), де Dк – відкритий ключ, може бути здійснений таким чином: ), де Dк – відкритий ключ, може бути здійснений таким чином:Зловмисник отримує системні параметри (однакові для обох користувачів) 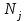 та відкритий ключ Ек. та відкритий ключ Ек. Використовуючи спеціальну криптоаналітичну систему, здійснюється факторизація модуля 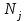 , у результаті чого він визначає прості числа , у результаті чого він визначає прості числа 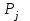 та та 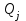 . .Розраховується значення функції Ойлера: 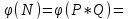 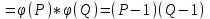 . .Використовуючи методику, наведену вище, здійснюється розв’язання рівняння 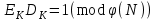 . .Взагалі, найбільш простим методом криптоаналізу є підбір ключової пари ( 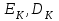 ), тобто при відомих ), тобто при відомих 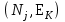 визначається Dк. визначається Dк.Проведені дослідження підтвердили, що необхідний рівень стійкості в RSA забезпечується в тому разі, якщо прості числа є сильними. Згідно із сучасними поглядами, найбільш перспективними методами криптоаналізу є методи, що базуються на пп. 1-4, розглянутих вище. При цьому найбільш складна задача факторизації модуля N вимагає найбільших ресурсів і суттєво залежить від методу, що використовується. На сьогодні відомо й апробовано такі методи факторизації[20-23, 121]: спробного поділу; 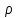 -Полларда і -Полларда і 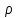 -1 Полларда; -1 Полларда;Ленстра, з використанням еліптичних кривих; квадратичне решето; загальне та спеціальні решета числового поля тощо. Найбільш перспективним, з точки зору мінімізації складності факторизації модуля, є метод, що реалізований у вигляді загального решета та спеціального решета числового поля. У таблицях 1.8 та 1.9 наведені узагальнені результати , які отримано вченими різних країн при розв’язуванні задач факторизації. Більш детально, в міру необхідності результати дослідження та оцінки RSA наведено в 6 розділі цієї монографії. 1.6.5 Сутність та аналіз крипто перетворення в скінченному полі Використання загальних параметрів та генерування асиметричної ключової пари.. Нехай F(p). просте скінченне поле(Галуа). Спочатку третя довірена сторона генерує загальні параметри 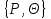 , де , де 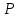 – просте, як правило, «сильне» просте число, а – просте, як правило, «сильне» просте число, а 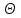 – первісний елемент. Далі всі користувачі генерують випадково за принципом «сам – собі» – первісний елемент. Далі всі користувачі генерують випадково за принципом «сам – собі» 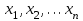 – особисті ключі, та зберігають їх як таємні, причому – особисті ключі, та зберігають їх як таємні, причому 1 < хі < Р–1 (1.132 Потім кожен користувач обчислює відкритий ключ, використовуючи загально системні параметри 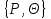 , тобто обчислює : , тобто обчислює :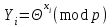 (1. 133) (1. 133)Приклад генерування ключів для двох користувачів наведено в табл. 1.10. Таблиця 1.10 Генерування асиметричної пари ключів у скінченному полі
Відкритий ключ сертифікують, тобто виготовляють сертифікат відкритого ключа: 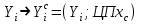 , (1.134) , (1.134)де 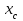 – особистий ключ сертифікації третьої довіреної сторони. – особистий ключ сертифікації третьої довіреної сторони.Створюється база всіх сертифікатів і до неї додається разом із загальними параметрами:ключ сертифікації центра: 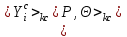 (1.135) (1.135)Алгоритм зашифрування. Нехай потрібно направлено зашифрувати повідомлення М, Повідомлення розбивається на блоки довжиною l 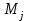 . Алгоритм зашифрування здійснюється таким чином. . Алгоритм зашифрування здійснюється таким чином. Генерується особистий ключ сеансу зашифрування: gричому 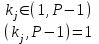 , (1.136) , (1.136)2. Обчислюється відкритий ключ сеансу: 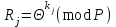 (1.137) (1.137)3. Обчислюється відкритий ключ направленого зашифрування: 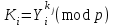 , (1.138) , (1.138)де 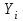 – відкритий ключ одержувача. – відкритий ключ одержувача.4. При зашифруванні користувач А, використовуючи свій ключ сеансу ka,,– відкритий ключ одержувача В - 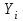 , і зрозуміло, загальні параметри , і зрозуміло, загальні параметри 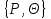 , обчислює блок-криптограму Сi, а також відкритий ключ сеансу , обчислює блок-криптограму Сi, а також відкритий ключ сеансу 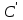 : :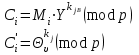 , (1.139) , (1.139)де 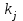 – особистий ключ сеансу того, хто зашифровує. – особистий ключ сеансу того, хто зашифровує.Далі користувач А передає пару 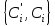 користувачу В . користувачу В .Алгоритм розшифрування. Розшифрування користувачем - отримувачем здійснюється таким чином. 1. Користувач В знає загальні параметри  , що є ідентичними параметрам користувача А. , що є ідентичними параметрам користувача А.2. Знаючи свій особистий ключ ХВ, користувач В направлено розшифровує криптограму 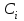 , поділивши , поділивши 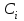 на на 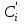 , тобто , тобто 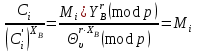 . (1.140) . (1.140)3. Якщо помилок у криптограмі 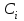 та відкритому ключі сеансу та відкритому ключі сеансу 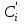 немає, і особистий ключ ХВ застосовується правильно, то користувач В отримує відкритий блок – повідомлення немає, і особистий ключ ХВ застосовується правильно, то користувач В отримує відкритий блок – повідомлення 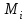 . .Таким чином, криптографічне перетворення в скінченному полі є зворотним і однозначним. Відносно стійкості перетворення в скінченному полі, то потрібно відмітити, що складність криптоаналізу методом повного розкриття зводиться до дискретного логарифмування в скінченному полі[20-23,121]. У таблиці 1.9 наведені узагальнені результати , які отримано вченими різних країн при розв’язуванні задач дискретного логарифмування. Більш детально, в міру необхідності, результати дослідження та оцінки крипто перетворення в скінченному полі, а також проблемні питання, наведено в 6 розділі цієї монографії. 1.6.6 Сутність та аналіз крипто перетворення НШ у групі точок еліптичної кривої Дослідження та практичне застосування показали, що основним недоліком криптоперетворень НШ у полі Галуа є субекспоненційний характер складності атаки дискретного логарифмування при спробі визначити особистий ключ. Зазначене протиріччя може бути обійдене при застосуванні НШ Ель - Гамаля криптографічних перетворень у групі точок еліптичної кривої[20-23, 48-49, 237,264, 345]. Перед вивченням цього матеріалу рекомендується, принаймні ознайомитися, з математичним апаратом еліптичних кривих [20-21, 239,267, 36-38]. Перелік і сутність загальних параметрів. До загальних параметрів еліптичної кривої над скінченним полем належить кортеж (а, в, G, n, P, u, h), (1.141) де 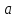 та та 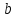 – параметри еліптичної кривої, які визначають рівняння еліптичної кривої – параметри еліптичної кривої, які визначають рівняння еліптичної кривої 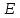 , що використовується, , що використовується, 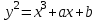 ; ; 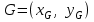 – базова точка порядку – базова точка порядку  з координатами з координатами 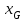 та та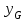 ; ;  – порядок базової точки – порядок базової точки 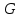 за умови, що за умови, що 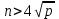 та та  – просте число; – просте число;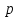 – розмір поля, який визначає базове кінцеве поле – розмір поля, який визначає базове кінцеве поле 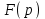 , де , де 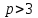 має бути простим числом; має бути простим числом; u =  – порядок еліптичної кривої; – порядок еліптичної кривої;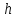 – коефіцієнт взаємозв’язку порядку кривої – коефіцієнт взаємозв’язку порядку кривої 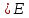 та порядку базової точки та порядку базової точки  , причому , причому 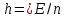 . .До загальних параметрів еліптичної кривої над полем Галуа F(2m) належить кортеж (а, в, G, n, (f(x), m),u, h), ( 1.142) де 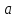 та та 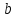 – параметри еліптичної кривої, які визначають рівняння еліптичної кривої – параметри еліптичної кривої, які визначають рівняння еліптичної кривої 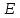 , що використовується, , що використовується, 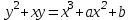 ; ; 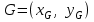 – базова точка порядку – базова точка порядку  з координатами з координатами 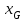 та та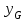 ; ;  – порядок базової точки – порядок базової точки 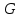 за умови, що за умови, що 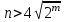 та та  – просте число; – просте число; (f(x), m) – примітивний поліном та його степінь; u = 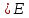 – порядок еліптичної кривої; – порядок еліптичної кривої;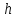 – коефіцієнт взаємозв’язку порядку кривої – коефіцієнт взаємозв’язку порядку кривої 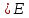 та порядку базової точки та порядку базової точки  , причому , причому 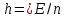 . .Криву, тобто її параметри, ні в якому разі не можна вибирати з переліку значень, що не рекомендуються або заборонені. До загальних параметрів еліптичної кривої над полем Галуа F(рm) належить кортеж (а, в, G, n, рm,u, h), (1.143) де 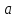 та та 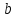 – параметри еліптичної кривої, які визначають рівняння еліптичної кривої – параметри еліптичної кривої, які визначають рівняння еліптичної кривої 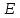 , що використовується, , що використовується, 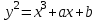 ; ;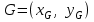 – базова точка порядку – базова точка порядку  з координатами з координатами 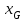 та та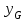 ; ; – порядок базової точки – порядок базової точки 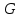 за умови, що за умови, що 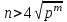 та та  – просте число; – просте число;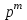 – розмір поля, який визначає базове кінцеве поле – розмір поля, який визначає базове кінцеве поле 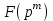 , де , де 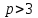 має бути простим числом; має бути простим числом;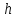 – коефіцієнт (кофактор) взаємозв’язку порядку кривої u – коефіцієнт (кофактор) взаємозв’язку порядку кривої u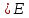 та порядку базової точки та порядку базової точки  , причому , причому 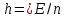 . .Криву, тобто її параметри, ні в якому разі не можна вибирати з переліку значень, що не рекомендуються або заборонені. Усі параметри еліптичної кривої мають генеруватися випадково. Генерування асиметричної ключової пари. Ключова пара 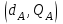 , (1.134) , (1.134)де 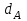 – особистий ключ, – особистий ключ, 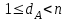 генерується випадково, а відкритий ключ генерується випадково, а відкритий ключ 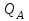 обчислюється способом виконання скалярного множення обчислюється способом виконання скалярного множення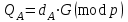 , (1.135) , (1.135)де G – базова точка на еліптичній кривій порядку n, а QA – відкритий ключ, що є точкою на еліптичній кривій з координатами (ха, уа). Також існує тривимірне подання ЕК, що називається проективною геометрією (базисом). У проективній геометрії кожна точка задається трьома координатами – X, Y, Z. Основною операцією в групі точок ЕК є скалярне множення вигляду (1.135) для скінченного простого поля F(p), а для розширення F(2 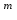 ): ): 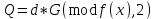 . (1.136) . (1.136)Стійкість атаки проти загрози повного розкриття визначається складністю розв’язання рівнянь (1.135) і (1.136) відносно особистого ключа d. Складність розв’язування цього рівняння набагато вища, ніж у кільці та скінченному полі. У скінченному полі – субекспоненційна, а в групі точок еліптичних кривих – експоненційна складність. Направлене зашифрування блоків інформації. При зашифруванні повідомлення М, розбивається на блоки 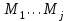 , довжина яка задовольняє вимоги , довжина яка задовольняє вимоги 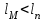 , тобто менше довжини модуля ln, , тобто менше довжини модуля ln, 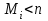 . Зашифрування здійснюється за правилом: . Зашифрування здійснюється за правилом: 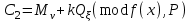 , ( 1.137) , ( 1.137)де k – ключ сеансу (сеансовий), 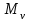 подається у вигляді точок еліптичної кривої, а подається у вигляді точок еліптичної кривої, а 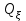 – відкритий ключ отримувача. – відкритий ключ отримувача.Також обчислюється відкритий ключ сеансу 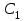 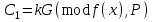 , (1.138) , (1.138)де G – базова точка на еліптичній кривій. Далі відправник передає користувачеві (одержувачу) 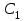 - відкритий ключ сеансу та - відкритий ключ сеансу та 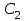 – криптограма. – криптограма.Направлене розшифрування криптограми. Розшифрування криптограми 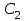 здійснюється за умови, що: здійснюється за умови, що:одержувач 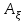 володіє особистим ключем володіє особистим ключем 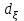 ; ;знає загальні параметри відповідної еліптичної кривої; отримав і має достовірні значення пари (С1, С2) Розшифрування виконується таким чином. Користувач 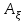 бере бере  , що має бути точкою на еліптичній кривій і визначає , що має бути точкою на еліптичній кривій і визначає 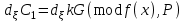 . (1.139) . (1.139)Потім отриману точку 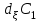 він віднімає від криптограми С2, тобто обчислює він віднімає від криптограми С2, тобто обчислює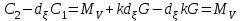 . (1.140) . (1.140)Із (1.140) слідує, що криптографічне перетворення в групі точок еліптичної кривої є зворотним і однозначним. Попередня оцінка криптографічної стійкості. Попередню оцінку криптографічної стійкості розглянемо на прикладі атаки «повне розкриття»[ 6, 20-23]. Для цього розглянемо проблему розв’язання дискретного логарифма в групі точок еліптичної кривої. Нехай є точки ЕК 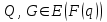 , необхідно розв’язати порівняння (1.135 3.32) чи (1.136 3.33) відносно d. Для загального випадку еліптичної кривої над полем F(pm) порівняння має вигляд , необхідно розв’язати порівняння (1.135 3.32) чи (1.136 3.33) відносно d. Для загального випадку еліптичної кривої над полем F(pm) порівняння має вигляд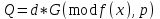 (1.141) (1.141) Деякі проблемні питання НШ в групі точок еліптичної кривої. По перше проблемність полягає в тому, що 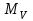 має бути точкою на ЕК. Тобто перед зашифруванням блоки інформації необхідно подати у вигляді точок еліптичної кривої. Ця задача хоча і є поліноміально складною, але за складністю має такий самий порядок, що й шифрування, що . зменшує швидкодію НШ. По друге недоліком загального алгоритму є те, що він має дуже велику складність, так як для кожного блоку потрібно генерувати k і виконувати скалярне множення, обчислюючи kG та має бути точкою на ЕК. Тобто перед зашифруванням блоки інформації необхідно подати у вигляді точок еліптичної кривої. Ця задача хоча і є поліноміально складною, але за складністю має такий самий порядок, що й шифрування, що . зменшує швидкодію НШ. По друге недоліком загального алгоритму є те, що він має дуже велику складність, так як для кожного блоку потрібно генерувати k і виконувати скалярне множення, обчислюючи kG та 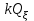 . .Більш детально, в міру необхідності, результати дослідження та оцінки крипто перетворення в групі точок еліптичної кривої, а також проблемні питання, наведено в 6 розділі цієї монографії. 1.6.7 Сутність та аналіз крипто перетворення НШ у фактор - кільцях Всередині 1990-х років групою математиків (Джефрі Ховстейн, Джилл Піфер та Джозеф Сильверман) було розроблено новий метод НШ в фактор - кільці. В подальшому він отримав назву NTRU [217, 20-21]. Вперше офіційно крипто перетворення в фактор - кільці було представлено на конференції CRYPTO 96. У подальшому метод, а потім і алгоритм НШ в фактор - кільці було доопрацьовано, наприклад, збільшено розміри параметрів алгоритму з метою підвищення криптографічної стійкості. У подальшому автори роботи [217] довели, що найбільш ефективним методом криптоаналізу цієї системи є атака за допомогою зведення в алгебраїчній решітці. У квітні 2011 року Американським комітетом X9 NTRU був затверджений у вигляді стандарту ANSI X9.98 [217]. Основними його перевагами при застосуванні для НШ стало можливість забезпечення високого рівня стійкості та значного зменшення у порівнянні з відомими складності НШ. Нині спостерігається суттєвий інтерес до крипто перетворень в фактор - кільцях та розширюється його застосування. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||