1 Методи та механізми 2014. 1. 1 Основні послуги при застосуванні, уніфікація та стандартизація криптографічних перетворень
 Скачать 1.75 Mb. Скачать 1.75 Mb.
|
|
5) Атака на основі підібраного шифро тексту. На відміну від попередніх атак, при здійсненні цієї атаки криптоаналітик може вибирати шифр-тексти Сi= Ек(Мi) та він має засіб з уведеним у нього секретним ключем К. Його завданням дешифрувати вибрані шифр-тексти, тобто отримати Мi. Особливістю цієї атаки є те, що криптоаналітик має засіб розшифрування з введеним в нього ключем, але ключ йому не доступний ніяким чином. Визначений таким чином ключ (ключі) криптоаналітик може використати для розшифрування інших шифр-текстів, які отримані із застосуванням цього ключа (цих ключів). У даному випадку атака здійснюється таким чином. Задано: С1, М1 = D к (C1); C2, M 2 = D к (C2); …, Ci, Mi = D к (Мi), (1.51) причому криптоаналітик може вибирати D1,. D2, …, Di. Необхідно визначити: ключ К, що міститься в засобі в недоступній формі. Розглянута атака в основному може бути застосованою відносно криптосистем з відкритим ключем, а також, за деякими обмеженнями, й щодо симетричних криптосистем. 6) Атака на основі підібраного ключа. При здійснені такої атаки ключ може підбиратись, якщо він зв’язаний з іншими ключами, вибирається з обмеженої множини, має певні відомі крипто аналітику властивості або генерується засобами, що мають погані властивості нерозрізнюваності(випадковості) та корельовані між собою тощо. Прикладом таких ключів можуть бути зв’язані між собою таємні (особисті) ключі [20,21, 118], циклові ключі блокових симетричних шифрів тощо. 7) Грабіжницький «аналіз». У даному випадку ключ (ключі) отримуються на основі використання агентури, шпіонажу, шантажу власників ключів, їх підкупу, застосування тортур тощо. Якщо врахувати велику обчислювальну складність атак крипто аналітичних атак 1)–6), то як свідчить практика метод грабіжницького аналізу є найбільш ефективний і реальний. Необхідно відмітити, що існує значне число класифікацій загроз та атак, як правило вони є розширеними або суттєво розширеними. В подальшому вони розглядаються більш детально починаючи з класифікації тощо. Наведена вище класифікація скоріше всього тільки характеризує умови проведення атак. Визначення обчислювально стійкого крипто перетворення (крипто системи) та умов її реалізації. Згідно (1.17), під обчислювально стійкими криптосистемами (шифрами) будемо вважати такі, щодо яких складність криптоаналізу має експоненційний характер і значення безпечного часу набагато більше часу цінності інформації, тобто 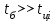 На практиці обчислювально стійкі криптосистеми (шифри) називають шифрами з гарантованою крипто стійкістю. В якості прикладів таких шифрів можна назвати блокові та потокові симетричні шифри. Визначимо модель та розглянемо умови реалізації обчислювально стійкого крипто перетворення (криптосистеми) на прикладі застосування симетричних шифрів. Особливістю обчислювально стійких криптосистемах, на відміну від безумовно стійких, замість ключової послідовності Кi, що використовується в безумовно стійких шифрах, використовується гама шифрування Г i. Зашифрування здійснюється складанням символів повідомлення 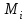 та гами зашифрування та гами зашифрування 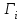 за модулем m та має вигляд: за модулем m та має вигляд: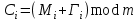 (1.52) (1.52)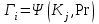 , (1.53) , (1.53)Функція (1.53) визначає правило генерування гами 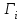 , , 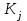 – вихідний (початковий, робочий, діючий) ключ, причому гама шифрування генерується у відповідності з цим ключем та діючими параметрами – вихідний (початковий, робочий, діючий) ключ, причому гама шифрування генерується у відповідності з цим ключем та діючими параметрами 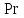 шифру (блочного чи поточного). шифру (блочного чи поточного). Розшифровування шифр-тексту здійснюється відніманням символів криптограми 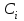 від символів гами розшифрування від символів гами розшифрування 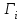 за модулем m та має вигляд: за модулем m та має вигляд: 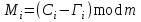 (1.54) (1.54)Аналіз показав, що в якості основних умов забезпечення обчислювальної стійкості є такі [20,21, 118, 147]. Гама 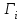 має генеруватись спеціальними засобами – генераторами гами. має генеруватись спеціальними засобами – генераторами гами.Символи гами 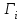 мають генеруватись випадково, рівно ймовірно, незалежно та одно рідно. мають генеруватись випадково, рівно ймовірно, незалежно та одно рідно. Період повторення гами 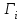 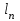 має бути не менше допустимої величини lд, тобто має бути не менше допустимої величини lд, тобто 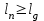 (1.55) (1.55)Закон формування гами повинен забезпечувати непередбачуваність гами. Ця вимога означає, що складність обернення рівняння (1.53), тобто знаходження ключа 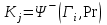 (1.56) (1.56)повинне мати експоненційний характер. В якості показника оцінки складності гами можна використовувати поняття її структурної скритності, наприклад, у вигляді[20, 21, 23]: 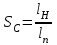 , (1.57) , (1.57)де lн – число символів гами, які потрібно знати для розкриття тих, що залишились, тобто lп – lн. Згідно (1.57) гама 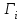 буде повністю непередбачувано, якщо буде повністю непередбачувано, якщо 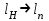 , а значить Sc , а значить Sc 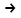 1. 1.Відновлюваність гами 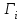 у просторі й часі, тобто наявність можливості генерувати ідентичні гами на різних станціях та в різний час. у просторі й часі, тобто наявність можливості генерувати ідентичні гами на різних станціях та в різний час.Забезпечення допустимих значень ймовірностей появи колізій, тобто ідентичних відрізків гами. Допустима складність (швидкодія) генерування гами у просторі й часі тощо. Необхідно відмітити, що у більшості випадків здійснюють шифрування(зашифрування, розшифрування) за модулем 2. Тоді правила шифрування (1.52 і (1.54) мають такий вигляд: 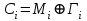 , (1.58) , (1.58)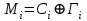 . (1.59) . (1.59)Для оцінки стійкості обчислювально стійкої криптосистеми можна використовувати показники та кортеж параметрів (Nk, H(К), 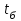 , γ, Ру, l0), що введені в п. 1.3.1. , γ, Ру, l0), що введені в п. 1.3.1. 1.3.4 Умови реалізації ймовірно стійких криптоперетворень Імовірно стійкі крипто перетворення (криптосистеми) типу шифрування називають направленими шифрами(НШ) [20, 21, 192,228]. Основною особливістю НШ є те, що ключ зашифрування Кз не співпадає (не повинен співпадати) з ключем розшифрування 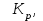 тобто тобто 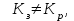 (1.60) (1.60)По суті за умови (1.60) ключ прямого перетворення 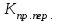 не повинен співпадати з ключем зворотного перетворення не повинен співпадати з ключем зворотного перетворення 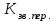 , тобто , тобто 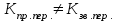 (1.61) (1.61)В асиметричній криптосистемі один із ключів асиметричної пари є таємним (особистим), а інший відкритим - його називають особистим. Основними умовами, які повинні бути обов’язково виконаними для реалізації ймовірно стійких криптоперетворень (криптосистем,шифрів) є наступні. Криптоперетворення направленого шифрування (зашифрування, розшифрування) здійснюється на основі асиметричного алгоритму з використанням асиметричної пари ключа. Асиметрична пара ключа складається, як мінімум, з особистого Ко (таємного) та відкритого Кв ключів. Направлене зашифрування здійснюється з використанням відкритого ключа Кв. 3) Направлене розшифрування використовується з використанням особистого ключа Ко. 4)Особистий Ко та відкритий Кв ключі є взаємозалежними, але існують алгоритми визначення одного із ключів за відомим іншим. 5) При направленому (асиметричному) шифрування мають застосовуватись загальні параметри криптографічних перетворень, але такі, що складність відомих атак має бути не нижче за субекспоненційну. 6) Асиметричне криптографічне перетворення направленого шифрування має дозволяти реалізацію моделі взаємної недовіри та взаємного захисту. 7) Асиметрична ключова пара (Ко , Кв), як правило, має генеруватись власником цієї пари ключів, тобто особистого ключа Ко. 8) Усі алгоритми та засоби криптографічних перетворень мають контролюватись і забезпечувати цілісність та справжність загальних параметрів та ключів. У відповідності з вимогами закону України « Про ЕЦП та електронні довірчі послуги» , а також по суті в основному відповідно з Регламентами 12 та 14[329,210], асиметричні крипто перетворення та реалізовані на їх основі криптосистеми і криптографічні протоколи , є основою якісного надання електронних довірчих послуг. Для надання вказаних електронних довірчих послуг в якості третьої довіреної сторони використовуються інфраструктури відкритого ключа. Незважаючи на короткий історичний період, вони мають теоретичну та практичну історію появи, розроблення, створення та розвитку. Перші роботи в цьому напрямку стали актуальними після винаходу асиметричних криптографічних перетворень в в кільці[20,21,129,389]. Нині розроблено та застосовується значне число асиметричних криптографічних систем. Їх принциповою особливістю є те, що при виконанні криптографічних перетворень у них використовується одна або навіть декілька асиметричних пар ключів [20-23]. Розглядається та досліджуються декілька перспективних методів , що пов’язані перш за все із застосуванням криптографічних перетворень на ідентифікаторах зі спарюванням точок еліптичних кривих, на гіпереліптичних кривих, криптоперетворень в фактор кільцях, гібридні крипто перетворення на ідентифікаторах та алгебраїчних решітках тощо[217,20,15-17]. Можливість та умови застосування вказаних криптоперетворень вивчені теоретично, створені та випробовуються дослідні версії, розроблено рекомендації та обговорюється необхідність створення регіональних і міжнародних стандартів. Починаючи з 1992 року тільки у 2010 році значну дорогу пробили собі криптографічні перетворення типу шифрування, що ґрунтуються на перетвореннях в фактор - кільцях (урізаних кільцях поліномів). Нині вони закріплені в стандарті ANSI США Х9.98 [217, 20-21,53]. У таблиці 1.1 наведено характеристики, загально - системні чи загальні параметри, а також асиметричні ключі основні асиметричні крипто перетворення, що застосовуються або можуть застосовуватись для таких криптографічних перетворень, як направлене шифрування, як (електронний) цифровий підпис, узгодження та встановлення ключів [20, 202]. Як випливає з таблиці 1.1, у якості особистого (таємного) використовується ключ Di, із асиметричної пари ключа (Di, Ei), а у якості відкритого (сертифікат) Ei ключ. Для асиметричного криптографічного перетворення у скінченному полі (Галуа) у якості особистого ключа використовується ціле число Хi, а у якості відкритого (сертифікат) ключа направленого шифрування - елемент поля Yi. Таблиця 1.1 Асиметричні криптографічні перетворення для реалізації направленого шифрування
Для асиметричного криптографічного перетворення НШ в групі точок еліптичних кривих у якості особистого ключа використовується ціле число di , а у якості відкритого ключа (сертифікату) направленого шифрування використовується точка еліптичної кривої Qi При застосуванні криптографічного перетворення на гіпереліптичних кривих як сертифікат відкритого ключа використовується якобіан D2, а як особистий ключ – якобіан D1. При застосуванні криптографічного перетворення зі спарюванням точок еліптичних кривих як сертифікат відкритого ключа направленого шифрування використовується ключ QiD, а як особистий ключ – diD. Для асиметричного криптографічного перетворення у фактор - кільці в якості особистого ключа використовується поліном f степені N, а у якості відкритого (сертифікат) ключа направленого шифрування - елемент поля h. Особливий інтерес нині становлять ІВК, що ґрунтуються якраз на криптографічних перетвореннях у фактор - кільці [217,20,21]. Основною перевагою цього алгоритму є те, що він працює набагато швидше за звичайні алгоритми направленого шифрування з відкритим ключем, наприклад таких як RSA чи еліптичні криві. 1.3.5 Сутність, класифікація та аналіз симетричних криптоперетворень Сутність симетричних криптографічних перетворень. Сутністю , або основною особливістю симетричних криптоперетворень (шифрів) є те, що ключ зашифрування Кз ,як правило, співпадає з ключем розшифрування 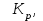 тобто [20] тобто [20]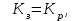 (1.62) (1.62)або один може бути обчисленим при знанні іншого не вище ніж с поліноміальною складністю. При цьому зашифрування здійснюється згідно (1.4), яке формально можна подати у вигляді 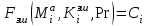 а розшифрування криптограми Сі згідно (1.5), тобто а розшифрування криптограми Сі згідно (1.5), тобто 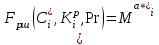 , , Для наведених перетворень якраз і виконується умова (1.62). Надалі в цьому пункті розглядаються симетричні криптографічні перетворення інформації. Як уже вказувалось криптографічну систему називають симетричною [147, 20,21], якщо ключ прямого перетворення 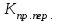 збігається з ключем збігається з ключем 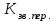 зворотного перетворення чи обчислюється один з одного з не вище ніж поліноміальною складністю. зворотного перетворення чи обчислюється один з одного з не вище ніж поліноміальною складністю. Класифікація симетричних криптографічних перетворень. Симетричні крипто перетворення поділяються на блокові шифри, потокові шифри та функції гешування (геш-функції) (рис. 1.6). Відповідно поняттю криптосистеми блокові шифри, потокові шифри та функції гешування якраз і є криптосистемами. Основною метою їх застосування є надання користувачам послуг конфіденційності, цілісності та доступності.  Рис. 1.6. Класифікація та призначення симетричних криптоперетворень У цілому необхідно відмітити, що побудування та аналіз блокових і потокових шифрів і функцій гешування пов’язане з використанням елементарних |
