1 Методи та механізми 2014. 1. 1 Основні послуги при застосуванні, уніфікація та стандартизація криптографічних перетворень
 Скачать 1.75 Mb. Скачать 1.75 Mb.
|
|
безумовно стійкі або теоретично не дешифровані, тобто такі, щодо яких криптоаналітик ніколи не зможе виконати криптоаналіз як практично, так і теоретично; 2) обчислювально стійкі, щодо яких можна виконати криптоаналіз, але при вибраних у шифрі параметрах і ключах на нинішньому етапі розвитку криптоаналізу, доступних ресурсів недостатньо для вирішення задачі криптоаналізу в допустимі часові інтервали; 3) ймовірно стійкі, доведення стійкості щодо яких зводиться до розв’язання математичної або математичних задач, складність розв’язання яких не доведена та може бути з часом зменшена, наприклад, зведена з експоненційно складної до субекспоненційно складної. 4) обчислювально нестійкі, у таких шифрах складність криптоаналізу на межі можливостей криптоаналітика, або при проектуванні у них вимушено чи через некомпетентність закладені слабкості. Зрозуміло, що така класифікація відображає певні погляди, які можна пояснити перш за все їх практичною спрямованістю при побудуванні та аналізі криптосистем. Тому одним із можливих варіантів класифікації шифрів за стійкістю є спосіб, коли для оцінки стійкості використовується критерій безпечного часу, що наводиться нижче[ 20 ]. Безумовно стійкими або теоретично не дешифрованими є криптосистеми (шифри), у яких при виконанні вимог щодо вибору параметрів та механізмів управління ключами, згідно сучасних поглядів, забезпечується умова: 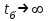 (1.16) (1.16) Обчислювально стійкими є криптосистеми (шифри), щодо яких складність криптоаналізу з певними параметрами оцінюється як експоненційно складна, і значення безпечного часу набагато більше часу цінності інформації, тобто 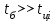 (1.17) (1.17)Ймовірно стійкі криптосистеми (шифри), щодо яких складність криптоаналізу оцінюється як експоненційно або субекспоненційно складна,причому доведення стійкості щодо яких зводиться до розв’язання математичних задач, складність розв’язання яких не доведена і значення безпечного часу набагато більше часу цінності інформації, тобто 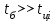 (1.18) (1.18) Обчислювально нестійкі криптосистеми (шифри), у яких складність криптоаналізу на межі можливостей криптоаналітика, або у які при проектуванні вимушено чи через некомпетентність закладені слабкості, а значення безпечного одного порядку або менше часу цінності інформації, тобто 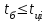 (1.19) (1.19) На наш погляд, запропонована класифікація дозволяє практично оцінити та порівняти крипто перетворення, криптосистеми та криптографічні алгоритми різної природи. Умови та приклади реалізації криптосистем з безумовним рівнем стійкості. Дотримуючись формалізованого підходу, розглянемо загальні умови та вимоги щодо побудування криптосистем з безумовною, обчислювальною (гарантованою), ймовірно стійкою та обчислювально нестійкою стійкістю криптосистеми. Розгляд та умови реалізації криптосистем розпочнемо у відповідності з рівнями гарантій стійкості. 1.3. 2 Умови реалізації безумовної стійкості в симетричних криптосистемах Визначення умов реалізації криптосистем безумовної стійкості є непростим і неоднозначним. Але на формальному рівні їх можна визначити, висунувши вимоги до практичної реалізації. В [147] на достатньо формальному рівні визначені необхідні та достатні умови забезпечення безумовної стійкості. Для захисту особливо критичної інформації в частині забезпечення високого рівня конфіденційності можуть використовуватися криптографічні перетворення, що забезпечують безумовну стійкість. Теорема 1.3[147]. Необхідною і достатньою умовою забезпечення безумовної стійкості симетричного крипто перетворення є умова, що: 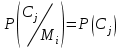 , (1.20) , (1.20) тобто ймовірність появи Сjкриптограми на виході засобу симетричного крипто перетворення шифратора не повинна залежати від того, яке Мі повідомлення з’явилося на виході джерела повідомлення. Інакше, ймовірність появлення криптограми має бути однаковою для всіх ключів і для всіх повідомлень. Це означає, що будь-яке повідомлення може зашифровуватись у будь-яку криптограму з однаковою ймовірністю. Доведення. Визначимо апостеріорну ймовірність 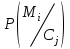 , яку може обчислити порушник (криптоаналітик), знаючи апріорні ймовірності , яку може обчислити порушник (криптоаналітик), знаючи апріорні ймовірності 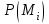 , , 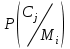 та та 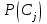 , використовуючи відому теорему теорії ймовірності та математичної статистики, у нашому випадку співвідношення (1.7): , використовуючи відому теорему теорії ймовірності та математичної статистики, у нашому випадку співвідношення (1.7):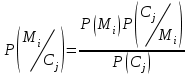 . (1.21) . (1.21)Нехай криптоаналітик перебуває щодо ІТС в умовах згідно з рис. 1.4. Ясно, що він не отримає ніякої інформації відносно джерела інформації (буде мати нульові знання), в умовах якщо 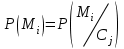 , (1.22) , (1.22)Дійсно, у цьому випадку згідно (1.10) 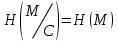 (2.23) (2.23) Підставивши (1.22) у (1.23), отримаємо, що 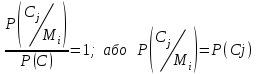 (2.24) (2.24)Таким чином, теорему 1.3.1 доведено для загальних умов. Приклади реалізації безумовно стійкої криптосистеми. Криптографічні системи, і зрозуміло криптографічні перетворення, для яких виконується ця умова і є безумовно стійкими [147, 20-21]. Прикладом реалізації такої системи є система Вернама. У цій системі здійснюється потокове шифрування, тобто символи криптограми в шифраторі зашифруються згідно з правилом: 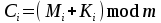 , (1.25) , (1.25)де Мi– i-й символ повідомлення, 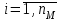 , а Кі – і-й символ ключа, Сі – i-й символ криптограми, m – розмір алфавіту, що використовується. , а Кі – і-й символ ключа, Сі – i-й символ криптограми, m – розмір алфавіту, що використовується.Відмінною рисою системи Вернама є те, що символи ключа Кi мають генеруватись (породжуватися) випадково, рівно ймовірно та незалежно. У такій системі символів ключа (довжина ключа) має бути не менше довжини повідомлення, тобто 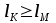 . (1.26) . (1.26)Розшифрування в системі Вернама здійснюється згідно з правилом: 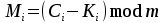 . (1.27) . (1.27)Аналіз (1.25) і (1.27) показує, що для зашифрування і розшифрування потрібно використовувати однакову випадкову послідовність (ключ). Показано, що для криптографічної системи, яка розглядається, умовна ентропія 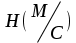 буде мати вигляд [7]: буде мати вигляд [7]: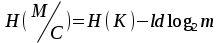 , (1.28) , (1.28)де l – довжина криптограми, d – надмірність алфавіту повідомлень. Визначимо умову, за якої реалізується безумовна стійкість, тобто знайдемо число символів криптограми, за якого не можна здійснити криптоаналіз. Задача криптоаналізу згідно (1.10) може бути розв’язана тоді, коли 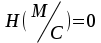 . .Тоді, підставивши це значення в з (1.28) отримаємо, що 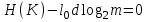 . (1.29) . (1.29)Далі, розв’язавши рівняння (1.29), отримаємо вираз для оцінки відстані єдності l0 для джерела ключів з ентропією 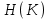 та збитковістю мови d алфавіту з основою m та збитковістю мови d алфавіту з основою m 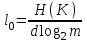 . (1.30) . (1.30)В (1.30) l0фізично означає мінімальну кількість символів криптограми, при правильному отриманні яких можна сподіватися на успішний криптоаналіз. Якщо l Також відомо, що, успіх криптоаналітика у розв’язанні задачі криптоаналізу залежить від обсягу криптограм, який він отримав. В звичайних умовах криптоаналітик перебуває у невизначеності (1.12), тобто 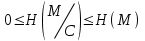 . Найкращий випадок для криптоаналітика буде, якщо . Найкращий випадок для криптоаналітика буде, якщо 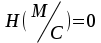 . .Для врахування умови (1.12) рекомендується використовувати поняття функції ненадійності Шеннона [7], що має такий вигляд: 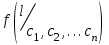 , (1.31) , (1.31)де l – загальний обсяг символів криптограми, який необхідно перехопити для розв’язання задачі криптоаналізу, а також враховуючи, що при l0 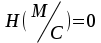 , можна скласти і розв’язати систему лінійних рівнянь і вона матиме один розв’язок. При цьому розв’язання самої задачі криптоаналізу може мати деяку довільну складність, в ому числі і не реалізуємо на практиці, тобто бути дуже складним, але воно існує за даних умов і воно єдине. , можна скласти і розв’язати систему лінійних рівнянь і вона матиме один розв’язок. При цьому розв’язання самої задачі криптоаналізу може мати деяку довільну складність, в ому числі і не реалізуємо на практиці, тобто бути дуже складним, але воно існує за даних умов і воно єдине. Кл. Шеннон для деякого класу лінійних (групових) шифрів, у яких використовуються природні мови (російська, англійська, С++, графіка), отримав розв’язок рівняння (1.28) [ 147, 20]. Замітимо, що надмірність d (1.28) і відповідно в (1.30) визначається залежністю символів мови між собою та різними ймовірностями появи їх у тексті. Вона може бути визначена з використанням співвідношення [147, 20-21] 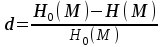 , (1.32) , (1.32)де Н0(М) – ентропія мови, де всі символи порівняно ймовірні та незалежні. Часткові випадки забезпечення безумовної стійкості. Якщо усі повідомлення рівно ймовірні, тобто 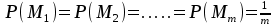 , (1.33) , (1.33)то 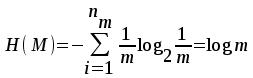 , ( 1.34) , ( 1.34)тому 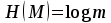 . (1.35) . (1.35)Використовуючи рівняння (1.30), для мови з двійковим алфавітом (m = 2) маємо що 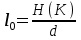 . (1.36 2.42) . (1.36 2.42)Показано, що для безумовно стійкого шифру[ 20] 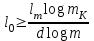 , коли , коли 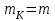 (1.37) (1.37)та 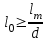 , коли , коли 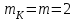 . (1.38) . (1.38)Іншою умовою забезпечення безумовної стійкості є умова, що [147,20 ]: 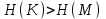 (1.39) (1.39)Таким чином, для безумовно стійкої системи l0 не менше довжини повідомлення і не менше довжини ключа, оскільки d<1. Тому для успішного криптоаналізу криптоаналітик повинен отримати не менш ніж lК символів, тобто весь ключ. Для безумовно стійкого крипто перетворення також має місце співвідношення, що 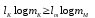 , (1.41) , (1.41)звідки отримаємо, що 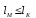 . (1.42) . (1.42)1.3.3 Умови реалізації обчислювальної стійкості криптоперетворень Основні умови здійснення криптоаналізу. Згідно прийнятих концепцій уточнимо умови проведення криптоаналізу та визначимо умови реалізації обчислювально та ймовірно стійких криптосистем (перетворень) [20, 21, 118]. Розгляд та аналіз проведемо з точки зору забезпечення конфіденційності, з метою визначення умов реалізації та загальних підходів до побудови шифрів – симетричних і асиметричних. При аналізі будемо вважати, що порушник (криптоаналітик) має необмежений доступ до каналів телекомунікаційних систем та у випадку рис. 1.5 і до носіїв інформації. В якості основного завдання криптоаналізу будемо вважати відновлення крипто аналітиком відкритого тексту без знання ключа або частини ключа, а також визначення самого ключа. При чому кожну із спроб здійснення криптоаналізу будемо називати крипто атакою. Необхідно відмітити, що фундаментальне припущення щодо криптоаналізу вперше було висловлено ще в ХІХ столітті датчанином А. Керкхоффсом, яке полягає в тому, що таємність інформації (повідомлення), що зашифровується, повною мірою має залежати тільки від ключа. Інакше, стійкість криптограми ґрунтується на забезпеченні конфіденційності ключа. Керкхоффс виходив із припущення, що криптоаналітик має всю необхідну інформацію щодо опису криптографічної системи та засобів її реалізації. Згідно нинішніх поглядів якраз в цих умовах має забезпечуватись задекларований рівень криптографічної стійкості. Якщо криптоаналітик не в змозі здійснити успішно криптоаналіз в умовах повних знань, то зрозуміло, що в умовах апріорної невизначеності тим паче він не зможе успішно здійснити атаку. При розгляді умов проведення криптоаналізу вважається, що криптоаналітик може проводити такі сім типів крипто аналітичних атак. При цьому для кожної із атак вважається, що криптоаналітик повністю знає криптосистему та з високою ймовірністю має доступ до криптограм. Для введеної на рис. 1.4 - 1.5 моделі існують такі атаки[ 20,21]. 1) Атака при відомому шифр-тексті. В ході здійсненні такої атаки вважається, що криптоаналітик знає все про криптосистему, має засоби її реалізації (зашифрування, розшифрування, управління ключами та має доступ до криптограм. Його задачами є дешифрування якомога більшого числа криптограм, тобто отримання відкритих текстів, а також розкриття (визначення) таємного ключа. У цих умовах він зможе розшифрувати всі повідомлення (інформацію), які були зашифровані на компрометованому ним ключі з використанням відповідного алгоритму Ек. Таким чином, атака проводиться в таких умовах. Задано: С1 = Е к (М1), С2 = Е к (М2), …, Сi = Е к (Мi). (1.43) Необхідно визначити: повідомлення М1, М2….., Мi, а краще ключ К, а значить і алгоритм визначення Мi+1 із Сi+1 = Е к (Мi+1). (1.44) 2) Атака на основі відомого відкритого тексу та відповідних йому шифр-текстів. На відміну від атаки 1) при здійсненні цієї атаки вважається, що криптоаналітик додатково має доступ до деякого числа шифр-текстів та відповідних їм відкритих текстів. Задача криптоаналітика визначити (розкрити) ключ (або ключі), які були застосовані при зашифрування вказаних повідомлень. Визначені ключі криптоаналітик може використати для дешифрування інших шифр-текстів, які отримані із застосуванням цього ключа (цих ключів). Тобто атака проводиться в таких умовах. Задано: М1, С1 = Е к (М1); М2, С2 = Е к (М2); …, Мi, Сi = Е к (Мi). (1.45) Необхідно визначити ключ К чи алгоритм визначення Мi+1 із Сi+1 = Е к (Мi+1) (1.46) 3) Атака на основі підібраного відкритого тексту. При здійсненні цієї атаки, крім даних для атаки на основі відкритого шифр-тексту та шифр-текстів, криптоаналітик може вибирати відповідним чином відкриті тексти та здійснювати їх зашифрування. Також криптоаналітик має засіб зашифрування з невідомим йому ключем, який він не може отримати безпосередньо з засобу КЗІ. Задача криптоаналітика визначити (розкрити) ключ (або ключі), які були застосовані при зашифрування відповідних повідомлень. Такий ключ чи ключі криптоаналітик може використати для уже простого розшифрування інших шифр-текстів, які отримані із застосуванням цього ключа (цих ключів). Атака проводиться таким чином. Задано: М1, С1 = Е к (М1); М2, С2 = Е к (М2); …, Мi, Сi = Е к (Мi), (1.47) причому криптоаналітик може вибирати М1,,. М2, …, Мi. Необхідно визначити ключ К чи алгоритм визначення Мi+1 із Сi+1 = Е к (Мi+1) (1.48) 4) Атака на основі адаптивно підібраного відкритого тексту. Особливістю цієї атаки є те, що вона виконується з використанням спеціально підібраного тексту (текстів), а також при знанні даних для атаки на основі підібраного тексту. При цьому у подальшому криптоаналітик може уточнювати вибір наступного тексту в залежності від отриманих попередніх результатів, у тому числі вибирати блоки меншої довжини. Визначений ключ (ключі) криптоаналітик може використати уже для роз шифрування інших шифр-текстів, які отримані із застосуванням цього ключа (цих ключів). У цьому випадку атака проводиться таким чином. Задано: М1, С1 = Е к (М1); М2, С2 = Е к (М2); …, Мi, Сi = Е к (Мi), (1.49) причому криптоаналітик може вибирати М1,... М2, …, Мi та є доступ до М1, С1 = Ек(М1). На основі отриманих даних вибирається М2, С2 = Ек(М2). Далі на основі отриманих даних вибирається Мi, Сi = Ек(Мi). Необхідно визначити ключ К чи алгоритм визначення Мi+1 із Сi+1 = Е к (Мi+1) (1.50) |
