основы метрологии. 1. 1 Основные понятия в области метрологии
 Скачать 442.37 Kb.
|
1.10 Однократное измерение.Во многих областях производственной деятельности, в обиходе, в торговле подавляющее большинство измерений являются однократными. В обычных условиях их точность вполне приемлема, а простота и обусловленные ей высокая производительность и низкая стоимость ставят их вне конкуренции. Особенности метрологического анализа однократного измерения заключаются в следующем: из множества возможных значений отсчета получается только одно (и используется); представление о законе распределения вероятности отсчета и его СКО формируется исключительно на основе априорной информации.  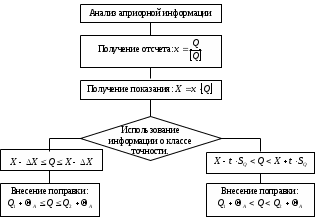 Рисунок 1.9 – Порядок действий при однократном измерении. Порядок действий при однократном измерении (рисунок 1.9) Предварительно проводят тщательный анализ априорной информации. Уясняется физическая сущность объекта измерений, уточняется его модель, устанавливаются влияющие факторы и принанимается решение о мерах по уменьшению влияния этих факторов (термостатирование, экранирование, компенсация полей). Определяются значения поправок, выбирается метод и средства измерения, разрабатывается методика измерений. Анализируется опыт подобных измерений в прошлом. Одним из итогов анализа априорной информации является вывод о достаточной точности однократного измерения для решения измерительной задачи. Получение одного значения отсчета – основная измерительная процедура. Отсчет является случайным значением измеряемой величины и не может полностью характеризовать ее. Получение одного значения показания Х средства измерения. Имеет ту же размерность, что и измеряемая величина. Далее порядок действий таков: Определение пределов, в которых находится значение измеряемой величины. Зная класс точности средства измерения, определяют предельную допустимую абсолютную погрешность и пределы в которых лежит значение измеряемой величины: 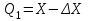 ;  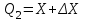(1.40)Внесение суммарной поправки. Осуществляется на основе анализа особенностей метода измерений и условий, в которых оно выполнялось. Поправка смещает Q1 и Q2, устанавливает пределы измеряемой величины. В качестве априорной информации может использоваться и опыт подобных измерений в прошлом. В конечном счете, необходимо знать закон распределения вероятности результата измерения и СКО. Показания могут подчиняться, например равномерному закону (из-за наличия люфтов) или нормальному закону. Во всех этих случаях значение измеряемой величины без учета поправки не отличается от случайного показания средства измерения Х больше, чем на половину доверительного интервала (нормальный закон) или на полуразмах (равномерный закон). Поправка при однократном измерении всегда вносится на последнем этапе. Пример 1: Микроамперметр класса точности 1.0 с диапазоном измерения от 0 до 100 мкА, внутренним сопротивлением 1кОм измеряет силу тока в цепи с суммарным сопротивлением 25кОм. Определить значение тока в цепи до включения в нее микроамперметра. Решение: 1. Априорной информацией является то, что имеются сведения о классе точности средства измерения и то, что при его включении в цепь сила тока уменьшится, следовательно, в показания прибора надо внести поправку. 2. Произведем измерение и получим значение отсчета. Пусть указатель остановится против отметки шкалы 40. 3. Определим показание прибора: 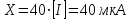 .4. Зная класс точности прибора и предельное значение шкалы, определим предельно допускаемое значение абсолютной погрешности: 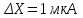 . Определим пределы, в которых находится сила тока через прибор: I1 = 39мкА; I2 = 41мкА.5. Анализирую метод измерения силы тока в цепи, устанавливаем, что в показания прибора целесообразно внести мультипликативную поправку 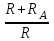 . Внесем поправку и определим пределы, в которых находится измеряемая величина: 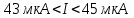 .Пример 2: Вольтметр измеряет напряжение. Известно, что показания прибора распределены по нормальному закону со значением SU=0.5В. При этом, вследствие смещения настройки прибор дает постоянно завышенные показания на 0.8В. Определить напряжение на сопротивлении, значение которого пренебрежимо мало по сравнению с сопротивлением вольтметра. Решение: 1. Указатель прибора установился против деления 10 – отсчет. 2. Показания прибора X=10В. 3. Задавшись доверительной вероятностью 0,95 для нормального закона распределения вероятности показания, определим доверительный интервал 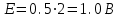 .Внесем аддитивную поправку в показания прибора и определим пределы в которых находится значение измеряемой величины: 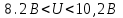 . |