основы метрологии. 1. 1 Основные понятия в области метрологии
 Скачать 442.37 Kb. Скачать 442.37 Kb.
|
1.9 Основы теории измерений1.9.1 Факторы, влияющие на точность измерений.Все в окружающем нас мире взаимосвязано и взаимообусловлено. Поэтому результат измерения, то есть то, что, мы получаем при проведении измерительной процедуры, определяется не только значением измеряемой величины, но и совместным влиянием целого ряда факторов, учет которых представляет иногда довольно сложную задачу. Объект измерений. Перед проведением измерения необходимо хорошо изучить объект измерения и представить себе модель исследуемого объекта, которая в дальнейшем, по мере получения измерительной информации, может уточняться. Чем точнее модель соответствует реальному объекту, тем корректнее измерительный эксперимент. Примеры: При измерении диаметра вала необходимо быть уверенным, что он круглый (иначе неясно какое значение принимать за диаметр). При контроле отклонений формы, наоборот измеряют отклонение от округлости. При измерении периода обращения Земли вокруг Солнца можно пренебречь неравномерностью периода, а можно, наоборот сделать его объектом исследования (измерения). При измерении меняющихся во времени величин часто определяют их средние значения, пренебрегая их измерением. В то же время, существует целое направление – Флуктуационные методы измерений и контроля. Оно основано на изучении флуктуаций (изменений) величины. С помощью этих методов получают необходимую информацию о качестве объекта измерений и осуществляют прогнозирование его технического состояния. Эксперт или экспериментатор – субъект измерений. Экспериментатор привносит в результат измерения элемент субъективизма, который, по возможности, необходимо стремиться уменьшить. Этот эффект зависит от квалификации измерителя, состояния его здоровья, соблюдения эргономических требований и т.д. Субъективная погрешность измерений исключается путем автоматизации измерений. Если нет возможности перехода к автоматизированным или автоматическим инструментальным измерениям, проводят комплекс мероприятий: к измерениям допускаются лица, прошедшие специальную подготовку, имеющие соответствующие знания, умения, практические навыки; последовательность действий экспериментатора строго регламентируется методикой выполнения измерений.  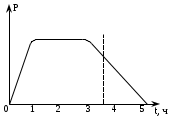 Рисунок 1.1 – Зависимость работоспособности экспериментатора от продолжительности его работы. Важное значение имеет режим работы экспериментатора, степень его устойчивости. На рисунке 1.1 представлен график зависимости работоспособности экспериментатора в течение рабочей смены.  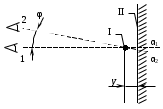 Рисунок 1.2:I –указатель; II – шкала. 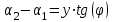 Важное значение имеют также санитарно-гигиенические условия труда: Освещенность – мелкие предметы различаются при освещенности 50…70лк. Максимальная острота зрения при освещенности 600…1000лк. При естественном освещении производительность труда примерно на 10% выше, чем при искусственном. Применяют три вида освещения: общее – освещение всего помещения (при проведении механических измерений невысокой точности); местное – освещение непосредственно рабочего места (при измерении применять не рекомендуется, так как получается неравномерное распределение яркости в поле зрения, что снижает производительность труда, приводит к появлению ошибок, повышает утомляемость). комбинированное – сочетание общего и местного освещения (при проведении высокоточных измерений, когда необходимо, чтобы свет на мелкие объекты падал под разными углами). При оптимальном освещении время ясного видения составляет 3 часа непрерывной работы. Для нормальной работы оператора измерительные приборы располагают в зоне, ограниченной углами 300 от оси в горизонтальной и вертикальной плоскостях. Отсчетные устройства располагаются перпендикулярно линии зрения оператора. Относительное расстояние от глаз до шкалы: 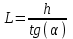 , где h – высота знака; α – угол, равный 40…500. , где h – высота знака; α – угол, равный 40…500. 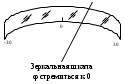 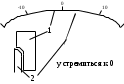 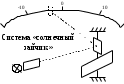  Рисунок 1.3 – Способы уменьшения погрешности параллакса. Неточность измерения, обусловленная субъективным фактором, называется субъективной или личной погрешностью. Одной из составляющих такого вида погрешности является погрешность параллакса, обусловленная отклонением от перпендикулярности, шкалы отсчетного устройства, к линии зрения оператора. Для определения этой составляющей рассмотрим рисунок 1.2. Применяются различные конструктивные приемы для уменьшения субъективной погрешности параллакса (рисунок 1.3). Уровень шума – не должен превышать 40..45дБ. Оказывает существенное влияние на результат измерения, на утомляемость и производительность экспериментатора. Часто для снижения утомляемости применяют функциональную музыку: мелодичные ненавязчивые мелодии со спокойным темпом. Рекомендуемое время звучания музыки – 1,5 …2,5часа за смену. Метод измерения. Оказывает существенное влияние на результат измерения. Примеры: 1) измерение сопротивления методом амперметра-вольтметра; 2) измерение ЭДС вольтметром; 3) измерение времени (время течет непрерывно, а сигнал поступает дискретно). Неточность измерений, обусловленная несовершенством метода измерения, называется погрешностью метода или теоретической погрешностью. Средство измерения. Оказывает двоякое действие на результат измерения. С одной стороны, подключение СИ к объекту измерения может привести и как правило приводит к некоторым изменениям измеряемых величин. Пример: 1) измерение тока амперметром; 2) измерение температуры жидкости ртутным термометром. С другой стороны, само СИ, в силу ряда причин, допускает неточность при измерении входной величины. К этим причинам можно отнести: нелинейность функции преобразования СИ, которая заменяется линейной; отклонения действительных значений параметров деталей и элементов СИ от заданных значений; износ деталей и элементов СИ; зазоры в подвижных соединениях, приводящие к неопределенности во взаимном положении деталей; наводки при работе электронных устройств; паразитные емкости и индуктивности и т.д. Неточность измерения, обусловленная используемыми СИ, называют инструментальной погрешностью измерений. Условия измерения. Это температура окружающей среды, влажность, давление, электромагнитное и гравитационное поля, напряжение в сети, вибрация и т.д. Очевидно, что все эти факторы влияют на результат измерения, поскольку они приводят к изменениям параметров и размеров деталей и элементов СИ, приводят к возникновению различных помех (изменение сопротивления от температуры – ТКС, изменение линейных размеров от температуры). Неточность измерений, вызванная условиями измерений, называют погрешностью от изменения условий измерения. 1.9.2 Основной постулат метрологии.В процессе измерения неизвестный размер сравнивают с известным, который обычно принимают за единицу и выражают его через известный размер в дольном или кратном соотношении. Математически эту процедуру можно записать так: 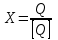 ; (1.9) ; (1.9)где X – отсчет по шкале; Q – измеряемая величина; [Q] – единица измерения. Выражение (1.9) называют уравнением измерения. В качестве [Q] при измерении физической величины выступает соответствующая единица СИ. Информация об этой единице заложена либо в используемой мере (метод сравнения с мерой), либо в разметке шкалы отсчетного устройства, в градировочной характеристике. При органолептических измерениях используется представление о размере величины, хранящемся в памяти человека. Следует отметить, что процесс сравнения осуществляется при воздействии множества как случайных, так и не случайных факторов, основные группы которых мы рассмотрели. Точный учет совместного влияния всех факторов невозможен, поэтому при многократном измерении одной и той же величины постоянного размера, результат сравнения X, называемый отсчетом, получается все время разным. Это положение, подтвержденное многолетней практикой, формулируется в виде аксиомы, которую называют основным постулатом метрологии – отсчет всегда является случайным числом. На основании отсчета определяется показание средства измерения: 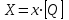 (1.10) (1.10)при этом, очевидно, что показание средства измерения является также случайным значением (X ≠ Q). Многие трудности в метрологии связаны с тем, что отсчет невозможно представить одним числом (величина случайная). Его можно как-то описать словами или математическими зависимостями. Пример: При n-кратном независимом измерении одной и той же физической величины постоянного размера аналоговым измерительным прибором указатель отсчетного устройства в случайной последовательности по M раз останавливался на каждом из делений шкалы:
Чему равен отсчет при таком измерении?  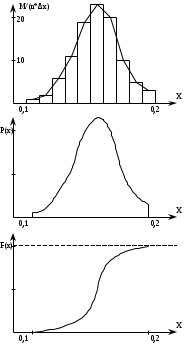 Рисунок 1.4 – Построение кривой распределения вероятности отсчета Решение: 1) Принимаем деления шкалы за основания и построим ни них прямоугольники с высотами, равными отношениям частот M/n к цене деления ΔX. 2) Полученная фигура (рисунок 1.4) называется гистограммой. Если соединить отрезками середины верхних сторон соседних прямоугольников, получим ломаную линию называемую полигоном распределения. Как гистограмма, так и полигон, являются исчерпывающим эмпирическим описанием отсчета. Если бы была возможность увеличить n, то в пределе при 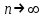 и и 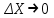 полигон преобразовался бы в плавную кривую – кривая плотности вероятности отсчета – p(x) (дифференциальная функция распределения плотности вероятности). полигон преобразовался бы в плавную кривую – кривая плотности вероятности отсчета – p(x) (дифференциальная функция распределения плотности вероятности).Построение можно выполнить иначе. Подсчитывая сколько раз указатель отсчетного устройства останавливался левее каждой отметки шкалы, откладывая над этой отметкой вдоль оси ординат отклонение числа таких отклонений к их общему числу n и соединяя полученные точки отрезками прямых, мы получим ломаную линию, называемую кумулятивной кривой. При 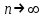 кумулятивная кривая преобразуется в интегральную функцию распределения вероятности отсчета – F(x). кумулятивная кривая преобразуется в интегральную функцию распределения вероятности отсчета – F(x).Плотность распределения вероятности p(x) и интегральная функция распределения вероятности F(x) служат математическими моделями законов распределения, получаемых из экспериментальных данных. Рассмотрим некоторые основные свойства законов распределения вероятности отсчета: интегральная функция распределения вероятности F(x) – определяет вероятность того, что отдельный результат сравнения по формуле (1.9) будет меньше x. F(x) – функция не убывающая, т.е. чем больше x, тем больше вероятность того, что результат сравнения по (1.9) не превысит это значение. При этом в случае изменения x от –∞ до +∞, F(x) изменяется от 0 до 1. Вероятность того, что результат измерения окажется в интервале (x1; x2) равна разности значений F(x) на границах этого интервала: 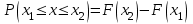 Описание отсчета с помощью законов распределения вероятности является наиболее полным, но неудобным. Обычно на практике используют приближенное описание закона с помощью его числовых характеристик или моментов. Все они представляют собой некоторые средние значения. Если величины усредняются относительно начала координат, то они называются начальными, если усреднение производится относительно центра распределения, то моменты называются центральными. Общее правило образования начальных моментов: 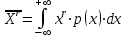 , где r – показатель степени. (1.11) , где r – показатель степени. (1.11)В метрологии широкое распространение находит начальный момент I-ого порядка, который называют математическим ожидание или средним значение отсчета: 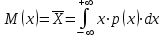 ; (1.12) ; (1.12)Свойства математического ожидания: 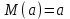 ; ; 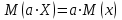 ; ; 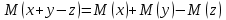 ; ; 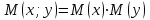 ; ;Математическое ожидание характеризует среднее значение отсчета. При этом экспериментально определить М(х) невозможно, поскольку для этого необходимо выполнить бесконечное число измерений ( 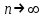 ). На практике используют лишь оценку математического ожидания – среднее арифметическое значение. При ). На практике используют лишь оценку математического ожидания – среднее арифметическое значение. При 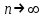 среднее арифметическое значение стремится к математическому ожиданию. среднее арифметическое значение стремится к математическому ожиданию.Мерой рассеяния результатов сравнения по формуле (1.9) относительно среднего значения является центральный момент II порядка, называемый дисперсией. 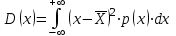 ; (1.14) ; (1.14)Свойства дисперсии: 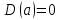 ; ; 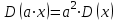 ; ; 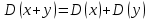 . .Чем больше дисперсия, тем значительнее рассеяние результатов сравнения относительно 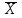 . Это наглядно видно из рисунка 1.5, где представлены кривые плотности распределения вероятности отсчета при различной дисперсии. . Это наглядно видно из рисунка 1.5, где представлены кривые плотности распределения вероятности отсчета при различной дисперсии. 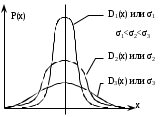 Рисунок 1.5 – Кривые плотности вероятности при различных дисперсия. В метрологии чаще используют среднеквадратическое отклонение (СКО) – σ. Среднеквадратическое отклонение, как и математическое ожидание, будучи характеристиками случайных законов распределения, сами не являются случайными, что очень удобно. Однако найти его опытным путем также невозможно, поэтому ограничиваются определением оценки среднего квадратического отклонения по формуле: 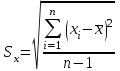 ; (1.16) ; (1.16)Математическими моделями эмпирических (опытных) законов распределения вероятностей отсчета могут быть различные законы распределения вероятности: закон Симпсона, Релея, Гаусса (нормальный закон распределения), равномерный закон и т.п. При этом наиболее подробного рассмотрения заслуживают 2 последних закона. Нормальный закон распределения вероятности (закон Гаусса).Является наиболее широко распространенным при описании эмпирических (опытных) данных. Имеет место, когда результат измерения определяется совместным действием большого числа факторов, среди которых нет доминирующего. Свойства нормального закона распределения вероятности: результат сравнения по (1.9) может принимать непрерывный ряд значений; вероятность появления отсчетов, для которых отклонения от среднего значения равны по модулю, но противоположены по знаку – одинакова. (симметричный закон); вероятность появления отсчетов уменьшается по мере возрастания отклонения от среднего значения; Кривая плотности распределения вероятности для нормального закона показана на рисунке 1.5, она имеет форму колокола. Дифференциальная p(x) и интегральная F(x) функции нормального распределения вероятности имеют вид: 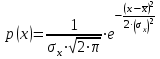 ; ;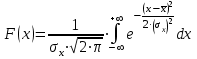 (1.17) (1.17)где σx – среднее квадратическое отклонение ( 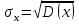 ; ; 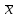 – среднее значение отсчета (его математическое ожидание)). – среднее значение отсчета (его математическое ожидание)).К важнейшим преимуществам нормального закона распределения относится его устойчивость, то есть при комбинации нормальных законов получается также нормальный закону. Вторым преимуществом является наличие различных табличных данных по данному закону, что упрощает процедуру его применения. Равномерный закон распределенияИмеет место, когда вероятность появления отсчета на некотором интервале значений измеряемой величины остается неизменной. Примеры: технологическое распределение сопротивлений резисторов; распределение диаметров шариков в подшипнике.  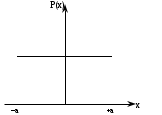 Рисунок 1.6 –Плотность равномерного и центрального распределения вероятности. В метрологии широко используют центрированный равномерный закон распределения (рисунок 1.6). Характеристики данного распределения: среднее значение отсчета – 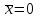 ; СКО – ; СКО – 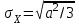 ; дисперсия – ; дисперсия – 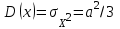 ; плотность распределения – ; плотность распределения – 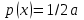 . .1.9.3 Учет влияющих факторов.Выше указывались основные группы факторов, влияющих на результаты измерения. Очевидно, что при проведении измерений необходимо каким-то образом учитывать эти факторы. В зависимости от этапа выполнения, мероприятия по учету факторов можно разбить на 3 группы. 1. Подготовка к измерениям. В период подготовки к измерениям факторы, влияющие на их результат необходимо (по возможности) исключить. Для этого особое внимание уделяют тщательному анализу свойств объекта измерения. К примеру, субъективная составляющая может быть существенно уменьшена путем соблюдения эргономических требований (они указаны выше). Большую роль в подготовке эксперимента играет правильно составленная методика выполнения измерений. Для исключения или уменьшения влияния условий измерений применяются различные мероприятия: применение средств измерений, имеющих специальное экранирование, термостатирование, амортизационные устройства (морской хронометр), стабилизаторы. 2. Процесс измерения. Если влияющие факторы не удалось исключить, то в процессе измерение их стараются скомпенсировать. Это достигается выполнением специальных методик выполнения измерения. Единых правил для этого нет, однако со временем выработались некоторые приемы, знание которых может быть полезным. Измерение методом замещения – примеры рассмотрены выше: взвешивание по методу Борда, Замещение в мостовой схеме. Компенсация влияющего фактора по знаку. Сущность заключается в том, что измерение проводят дважды, так, чтобы влияющий фактор оказывал противоположенное действие. За результат измерения принимается среднее арифметическое двух опытов. Пример: любая подвижная пара в механизме имеет зазор – люфт, что приводит (или может привести) к погрешности. Влияние люфтов может быть существенно уменьшено, если измерения проводить 2 раза: сначала со стороны меньших значений, а потом со стороны больших (например, овальность). Метод противопоставления. Применяется в случае, когда влияющий фактор приводит не к изменению результата измерения на некоторую величину, а к умножению его на некоторый коэффициент. Пример: взвешивание на равноплечих весах. Вначале производят обычное взвешивание: 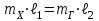 (1.18) (1.18)Затем груз устанавливают на другую чашу весов и вновь уравновешивают его гирями: 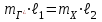 (1.19) (1.19)Искомое значение массы определяют из уравнения: 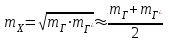 (1.20) (1.20)Метод симметричных измерений. Используется для исключения прогрессивного влияния какого-либо фактора, являющегося линейной функцией времени (постоянный нагрев аппаратуры, разряд аккумуляторов, потеря эмиссии радиоламп). Сущность: в течение некоторого интервала времени выполняется несколько измерений одной и той же величины постоянного размера и за окончательный результат принимается полу сумма отдельных результатов, симметричных по времени относительно середины интервала. 3. После измерения, если его не удалось организовать так, чтобы исключить или скомпенсировать какой-либо фактор, влияющий на результат, в последний иногда вносят поправки. Сущность поправок рассмотрим на примерах:  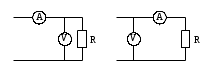 Рисунок 1.7 – Схемы измерения сопротивления методом амперметра-вольтметра. Пример 1. Измерение сопротивления методом амперметра-вольтметра. На рисунке 1.7 представлены 2 возможные схемы включения средств измерений. В первом случае из показаний амперметра необходимо вычесть ток, протекающий через вольтметр, то есть внести поправку в показания амперметра, равную в данном случае: 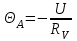 При значениях измерительного сопротивления, соизмеримых с сопротивлением вольтметра, эта поправка значительна. Во втором случае из показаний вольтметра необходимо вычесть падение напряжения на амперметре, то есть внести в показания вольтметра поправку: 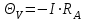 Эта поправка значительна при малых значениях R, соизмеримых с сопротивлением амперметра. Такие поправки называются аддитивными. Результат измерения получают путем прибавления аддитивной поправки к показаниям средства измерения: 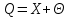 (1.21) (1.21)При этом результат измерения не равен значению измеряемой величины, поскольку результат измерения, как и отсчет, и показания, является величиной случайной. Пример 2. Измерение ЭДС вольтметром. В этом случае внутреннее сопротивление источника ЭДС обычно не учитывают. При этом вольтметр, согласно закону Ома, показывает не ЭДС, а падение напряжения на внутреннем сопротивлении вольтметра: 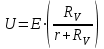 Таким образом, для исключения влияния метода измерения в данном случае необходимо умножить показание вольтметра на поправочный множитель: 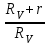 Такого рода поправки (поправочные множители) называют мультипликативными поправками. Результат измерения получается умножением показания средства измерения на мультипликативную поправку: 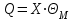 (1.22) (1.22)Результат измерения также является случайной величиной. Рассмотренные примеры иллюстрируют возможность учета с помощью поправок влияния несовершенство метода измерения. Аналогичные действия могут быть выполнены и для учета влияния условий измерений и средств измерений. Погрешность средств измерений, возникшая в результате влияния целого ряда факторов, всегда является случайной величиной. При этом, однако, часто погрешность имеет некоторую закономерную составляющую, приводящую к смещению среднего значения показания относительно значения измеряемой величины. То есть, средство измерения дает постоянно завышенное или заниженное значение. Закономерная составляющая погрешности средства измерения, которую ранее называли систематической погрешностью, может при повторных измерениях одной и той же величины оставаться неизменной или изменяться по определенному известному закону. В зависимости от характера изменения закономерной погрешности при изменении измеряемой величины, она может называться постоянной, прогрессивной, периодической (примеры: смещение начала отсчета – постоянная; погрешность при измерении времени (часы спешат или отстают) – прогрессивная; погрешность от эксцентриситета шкалы – периодическая). Указанные особенности средств измерений выявляются при их аттестации – всестороннем метрологическом обследовании. По итогам аттестации устанавливают поправку ΘСИ, которую необходимо вносить в показания средства измерения. Эта поправка может быть аддитивной или мультипликативной; числом или функцией; может задаваться графиком, функцией или таблицей. С учетом сказанного, результат измерения может быть представлен как: 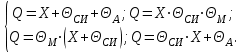 (1.23) (1.23)Необходимо помнить, что аддитивные поправки имеют размерность измеряемой величины, а мультипликативные поправки – безразмерны. Для иллюстрации приемов экспериментального определения поправок рассмотрим 2 способа. 1. Исследуемым прибором выполняют многократное измерение соответствующей образцовой меры, действительной значение которой известно с требуемой точностью. Поправку к показаниям средства измерения определяют как разность между значениями меры и средним арифметическим показанием прибора. 2. Одну и ту же величину измеряют образцовым и исследуемым прибором одновременно. При этом в каждом измерении добиваются одного и того же показания исследуемого прибора. Поправку определяют, как разность между средним арифметическим показаний образцового прибора и показанием поверяемого прибора. 1.9.4 Оценки результата измерения.После того, как влияние постоянно действующих и закономерных влияющих факторов исключено или учтено введение поправок, результат измерения остается случайным. Рассеяние отдельных значений результата измерения объясняется тем, что сравнение неизвестного размера с известным (получение отсчета) происходит в условиях воздействия множества случайных факторов (помех), точный учет совместного влияния которых невозможен. Поэтому для оценки закона распределения результата измерения необходимо провести многократное измерение, то есть несколько раз измерить одну и ту же величину. Применяют два вида оценок результата измерения – точечные и интервальные. 1.Точечные оценки – это оценки, которые выражаются одним числом. Предположим, что путем внесения поправок все закономерно изменяющиеся факторы учтены (выполнено исправление результата измерения). Тогда результат каждого отдельного сравнения при многократном измерении можно представить как: 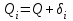 (1.24) (1.24)где δi – случайная погрешность результата измерения; Qi – результат i-того сравнения значения величины с мерой (измеренное значение величины); Q – значение измеряемой величины. В большинстве случаев δ распределена по одному из симметричных законов (как правило, по нормальному закону) распределения вероятности. Определим среднее арифметическое значение результата измерения: 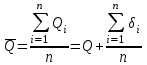 (1.25) (1.25)Для симметричных законов при достаточно большом n Σδi → 0, то есть среднее арифметическое стремиться к значению измеряемой величины: 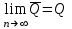 . .Вывод: При симметричных законах распределения вероятности результата измерения среднее арифметическое, будучи оценкой математического ожидания, является оценкой значения измеряемой величины. Мерой рассеяния отдельных результатов сравнения относительно среднего арифметического является среднее квадратическое отклонение, оценка которого определяется как: 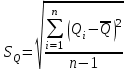 (1.27) (1.27)Отметим, что среднее арифметическое определяется по конечному ряду значений, каждое из которых является случайной величиной. Поэтому среднее арифметическое, а следовательно и среднее квадратическое отклонение, являясь оценками результата измерения, также будут случайными величинами. Мерой рассеяния среднего арифметического значения относительно значения измеряемой величины является среднее квадратическое отклонение среднего арифметического или так называемое стандартное отклонение, оценка которого определяется как: 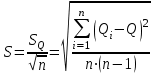 (1.28) (1.28)Видно, что с увеличением числа опытов точность многократного измерения возрастает («семь раз отмерь – один раз отрежь»). 2. Интервальные оценки. Точечные оценки 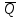 и S характеризуют результат измерения, при этом, однако, оценка по данным точечным характеристикам результата измерения не является наглядной и не дает непосредственной информации о том, чему же равно значение измеряемой величины. и S характеризуют результат измерения, при этом, однако, оценка по данным точечным характеристикам результата измерения не является наглядной и не дает непосредственной информации о том, чему же равно значение измеряемой величины.Смысл оценки результата измерения с помощью интервалов заключается в нахождении интервалов, называемых доверительными, между границами которых с определенной вероятностью (доверительной вероятностью) находится значение измеряемой величины. Пусть α означает вероятность того, что значение результата измерения не отличается от значения величины больше, чем не E, что можно записать в виде: 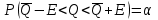 (1.29) (1.29)Тогда α – доверительная вероятность, а интервал значений от 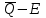 до до 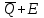 – доверительный интервал. – доверительный интервал.Очевидно, что доверительный интервал и доверительная вероятность связаны между собой чем больше α, тем больше должен быть Е. Таким образом, для оценки результата необходимо иметь два значения: доверительный интервал – оценка точности и доверительная вероятность – оценка надежности результата измерения. На практике обычно задаются определенной степенью надежности (доверительной вероятностью) и рассчитывают доверительный интервал. В машино- и приборостроении обычно задают α=90..95%. Для ответственных изделий может иметь место α=0,99% или даже α=0,999%. Значение Е определяется на основании точечных оценок. Если закон распределения результата измерения нормальный, то Е можно определить по табулированной функции: 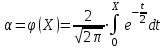 (1.30) (1.30)где x=E/S. Так, например, доверительный интервал ±S соответствует доверительной вероятности α=0,683. Вероятности α=0,954–Е=±2S, а вероятности α=0,997–Е=3S. Приведенные рассуждения правомочны, если имеется достаточно большое число экспериментальных данных (n>40..50). При технических измерительных обычно производят значительно меньшее число измерений. В случае, когда вероятность результата измерения распределяется по нормальному закону, а количество экспериментальных данных меньше 30…40, то среднее арифметическое подчиняется закону распределения вероятности Стьюдента (псевдоним В.С. Гассета) с тем же средним значением 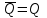 . .Не останавливаясь на математических выражениях для распределения Стьюдента, отметим, что значения функции также табулированы. На основании табличных данных, задаваясь доверительной вероятностью и числом экспериментальных данных – n, можно определить величину коэффициента Стьюдента – tα. Параметр tα играет в метрологии важную роль. Он показывает на сколько σ (СКО) с заданной вероятностью может отличаться случайное число, подчиненное нормальному закону распределения вероятности, от своего среднего значения. В данном случае tα показывает, насколько S (среднее арифметическое значение) может отличаться от значения измеряемой величины. Таким образом, доверительный интервал определяется как: 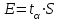 (1.31) (1.31)В отличие от нормального закона распределения, распределение Стьюдента дает значение tα зависимое от n. Так, например доверительный интервал ±2S имеет место для доверительной вероятности 0.86 (n=4); 0.90(n=6); 0.924(n=10); 0.940(n=20). При n>30 закон Стьюдента преобразуется в нормальный закон распределения вероятности. 1.9.5 Исключение ошибок.Надежность эргономической системы, куда входят объект измерения, человек, окружающая среда и средство измерения, не безгранична. В этой системе могут различного рода отказы. Причины таких отказов могут быть различными: отказ средства измерения, скачки напряжения в сети, сейсмические сотрясения, электромагнитные импульсы (локатор), отвлечение внимания оператора и т.п. В результате может возникнуть ошибка измерения, которую называют еще грубой погрешностью или промахом (если виноват оператор). При однократном измерении ошибка может быть обнаружена путем логического анализа и сопоставления результата измерения с заранее ожидаемым результатом (пример: напряжение в сети и получение 50В). При многократном измерении одной и той же величины ошибка проявляется в том, что результаты отдельных измерений значительно отличаются друг от друга. В этом случае необходимо решить вопрос о том, является ли данный результат ошибочным или он принадлежит закону распределения результата, который как известно, является случайным. Решение данного вопроса является обязательным, поскольку в случае ошибки результат многократного измерения может иметь большую погрешность. Для решения задачи исключения ошибок, очевидно, необходимо применить статистический подход. 1. отличие сомнительного результата от других настолько существенно, что ошибка очевидна. Необходимо установить причину ошибки, а ошибочный результат исключить. 2. Согласно центральной предельной теореме теории вероятности, результат измерения в случае, когда он определяется совместным влиянием большого числа факторов, вклад каждого из которых незначителен по сравнению с суммарным действием всех остальных, подчиняется нормальному закону распределения. Принимая закон распределения нормальным, что в большинстве случаев соответствует действительности, можно утверждать следующее: Если при многократном измерении одной и той же величины постоянного размера сомнительный результат отдельного измерения отличается от среднего арифметического больше чем на 3SQ, то с вероятностью 0,997 он является ошибочным, и его необходимо отбросить. Это правило называют правилом трех сигм. 3. В случае, когда количество экспериментальных данных меньше 25, используется метод проверки статистической гипотезы. Выдвигается гипотеза о том, что сомнительный результат Qi не является ошибочным, то есть является одним из значений случайного результата измерения. Зная закон распределения, проверяют эту гипотезу. В первую очередь, сомнительным может быть наибольший или наименьший из результатов. Поэтому для проверки гипотезы рассматривают закон распределения величин: 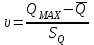 или или 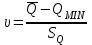 (1.31) (1.31)Функции распределения определяются методами теории вероятности. Они совпадают между собой и для нормального закона распределения вероятности результата измерения протабулированы. По данным соответствующих таблиц или заданной доверительной вероятности α и уровне значимости q=1–α, можно для чисел измерений 3…25 найти те наибольшие значения, υА, которые случайная величина υ может принять по чисто случайным причинам. Если вычисленное по экспериментальным данным значение υ окажется меньше υА, то гипотеза о том, что сомнительный результат – не ошибочный, принимается. В противном случае сомнительный результат можно отбросить, то есть рассматривать его как ошибку. После исключения ошибок необходимо заново найти точечные оценки закона распределения вероятности результата измерения. Отметим, что приведенные рассуждения справедливы лишь для нормального закона распределения вероятности. Поэтому, если такой уверенности нет, то указанное обстоятельство необходимо проверить. Методы проверки на нормальность распределения результата измерения будут рассматриваться ниже. 1.9.6 Измерительная информация.Измерение заключается в получении количественной информации об измеряемой величине. Необходимо отметить, что до выполнения измерения уже нужно иметь определенную информацию об измеряемой величине. Прежде всего, необходимо знать размерность величины, иначе неясно, с чем сравнивать при измерении с метром, секундой или рублем? Необходимо иметь хотя бы ориентировочное представление о диапазоне, в котором лежит значение величины (температуру в печи нельзя измерять уличным или медицинским термометром). Необходимо проанализировать объект измерения (внутренний диаметр шара нельзя измерить линейкой). При постановке любой измерительной задачи важно установить (исключить, скомпенсировать или учесть) влияющие факторы и т.п. Информация, которой располагают до выполнения измерения называется априорной. Второй постулат метрологии: Для проведения измерения необходимо иметь априорную информацию. Практически всегда можно указать ориентировочное значение величины. Если нельзя сказать какие из значений величины наиболее вероятны в установленных пределах, то остается принять что с одинаковой вероятностью измеряемая величина может иметь любые значения в интервале от Q1 до Q2, то есть воспользоваться математической моделью этой ситуации: 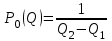 (1.32) (1.32)Дефицит информации об измеряемой величине состоит в неопределенности ее значения в интервале (Q1;Q2). Мерой неопределенности является энтропия: 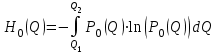 (1.33) (1.33)При равномерном законе распределения дефицит информации определяется как: 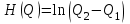 (1.34) (1.34)Рассмотрим теперь ситуацию после измерения. Выше было показано, что после измерения его результат может быть представлен также интервалом, в пределах которого с принятой вероятностью лежит значение измеряемой величины. Если принять, что закон распределения результата измерения известен, то вновь можно задаться равномерным законом в интервале (Q3;Q4), то есть опять представить ситуацию моделью: 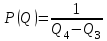 (1.35) (1.35)При этом значение измеряемой величины остается неизвестным. Остаточная неопределенность составляет: 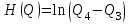 (1.36) (1.36)Таким образом, смысл измерения заключается в том, что найденный в результате измерения интервал меньше априорно известного, то есть измерение заключается в уточнении значения измеряемой величины. Определим, насколько уменьшился дефицит информации на основании измерений. 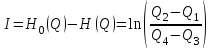 (1.37) (1.37)Величина I интерпретируется как количество информации получаемой в результате измерения, а протяженность интервалов (Q3;Q4) и (Q1;Q2) характеризует точность, с которой известно значение измеряемой величины до и после измерения. Если результат распределен по равномерному закону на интервале (а; b), то I определяется как: 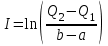 (1.38) (1.38)Если закон распределения вероятности результата измерения нормальный, то: 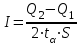 (1.39) (1.39) |
