основы метрологии. 1. 1 Основные понятия в области метрологии
 Скачать 442.37 Kb. Скачать 442.37 Kb.
|
1.12 Обработка результатов нескольких серий измерений.Часто возникают ситуации, когда многократное измерение одной и той же величины производится в несколько этапов, разными людьми, в разных местах, в разное время и на разных приборах. Результат такого измерения необходимо определять путем обработки нескольких серий результатов, которые могут отличаться по статистическим характеристикам. Серии называют однородными, если результаты в них подчиняются одному и тому же закону распределения вероятности. В противном случае серии считаются неоднородными. Обработка результатов нескольких серий зависит от того, однородны они или нет. Поэтому при задании способа обработки результатов обязательно производят проверку однородности серий. Обычно сравнивают средние арифметические и оценки дисперсий в каждой серии. Проверка производится в 2 этапа: проверка значимости различия между средними арифметическими; проверка равно рассеянности результатов измерений в сериях. 1. При проверке значимости различия между средними арифметическими вначале проводят обработку данных в каждой серии отдельно. При этом определяют значения средних арифметических ( 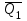 и и 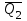 ), СКО ( ), СКО (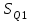 и и 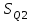 ) для каждой серии; производят проверку нормальности закона распределения. Затем определяют моменты закона распределения разности G ) для каждой серии; производят проверку нормальности закона распределения. Затем определяют моменты закона распределения разности G 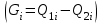 . Среднее . Среднее 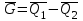 , СКО , СКО 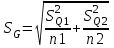 , где n1 и n2 – число результатов в первой и второй сериях. , где n1 и n2 – число результатов в первой и второй сериях.Если n1+n2>20..30, то, задавшись доверительной вероятностью p, по таблицам для нормального распределения определяют t и вычисляют доверительный интервал, как 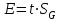 . Разность G не может оказаться за пределами этого интервала, если она является случайной и распределена по нормальному закону. Если выполняется условие: . Разность G не может оказаться за пределами этого интервала, если она является случайной и распределена по нормальному закону. Если выполняется условие: 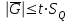 , то различия между средними арифметическими в сериях незначимы. , то различия между средними арифметическими в сериях незначимы.2. При проверке равно рассеянности результатов измерения в двух сериях после вычисления среднего арифметического и СКО для каждой серии и проверки нормальности результатов измерений в сериях определяют отношение дисперсий: 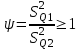 , которое подчиняется распределению Фишера. , которое подчиняется распределению Фишера.Задаются вероятностью P с которой принимается решение. По соответствующим таблицам определяют для выбранной вероятности P, значений n1 и n2 значение аргумента интегральной функции распределения вероятности Фишера ψ0. Если выполняется условие 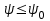 , то серии считаются равно рассеянными, если не выполняется – то серии считают неравно рассеянными. , то серии считаются равно рассеянными, если не выполняется – то серии считают неравно рассеянными.Равно рассеянные серии с незначимым различием между средними арифметическими считаются однородными. Если полученные экспериментальные данные определены в одних и тех же условиях, то говорят о сходимости измерений, если в разных – то о воспроизводимости измерений. Экспериментальные данные однородных серий обрабатывают как единый массив. Для сокращения вычислений применяют формулы: 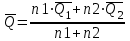 (1.54) (1.54)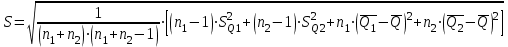 (1.55) (1.55)При обработке неравно рассеянных серий с незначимо различающимися средними арифметическими особенно ценные измерения учитываются с большей точностью. Последовательность обработки данных следующая: определяют среднее арифметическое в каждой серии 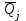 (j – число серий); (j – число серий);определяют СКО среднего в каждой серии Sj; определяют стандартное отклонение среднего взвешенного: 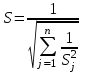 , где n – число серий (n=1..j). , где n – число серий (n=1..j).определяют среднее взвешенное: 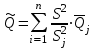 ; ;задаются доверительной вероятностью P; определяют n0 по таблицам t и рассчитывают доверительный интервал, как 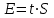 ; ;записывают результат измерения 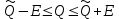 . .При обработке неравнорассеянных серий со значимым различием средних арифметических результаты измерений в каждой серии обрабатывают отдельно. При этом обработку проводят по правилам обработки результата многократного измерения. 1.13 Математические действия над результатами измерений.1.13.1 Функциональные преобразования результатов измерений. 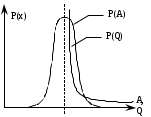 Рисунок 1.10 – Графики функций P(A) и P(Q). При использовании измерительной информации нередко производят различные математические действия над результатами измерений. При этом обязательно нужно учитывать, что результат измерения является случайным значением измеряемой величины. Обращение с результатами измерения, как с неслучайными значениями приводит к ошибкам. Любые функциональные преобразования результатов измерений связаны с изменением из законов распределения вероятности. Так, если Q=f(A), где А – результат измерения, а f – монотонная функция, то плотность распределения вероятности Q выражается через плотность распределения вероятности результата А измерения, как: 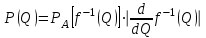 ; (1.58) ; (1.58)где f –1– функция обратная функции f. Пример: Q=A2, плотность распределения А: 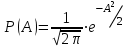 . Определить закон распределения вероятности результата измерения P(Q). . Определить закон распределения вероятности результата измерения P(Q).Решение: 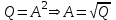 ; ;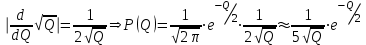 . .При сложных функциях и в случае, когда функция является функцией нескольких переменных, произвести указанные преобразования невозможно. В этом случае обычно ограничиваются определением приближенных оценок числовых законов. Пусть осуществляются косвенные измерения величины Q путем вычисления ее значения по результатам измерений А и В по известной зависимости Q=f(A; B). Предположим, что в результат измерения А и В внесены все необходимые поправки. Тогда А и В можно представить как: 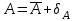 ; ; 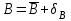 ; ; 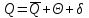 ; ;Идея приближенного вычисления заключается в том, что сложную функцию представляют рядом, в котором ограничиваются первыми членами разложения. Очевидно, что по сравнению с 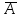 и и  значения δА и δВ достаточно малы, поэтому разложим функцию f в ряд Тейлора: значения δА и δВ достаточно малы, поэтому разложим функцию f в ряд Тейлора: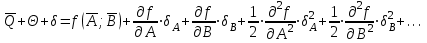 (1.59) (1.59)Из анализа выражения (1.59) видно, что первые слагаемые правой и левой частей не зависят от случайных отклонений, и следовательно: 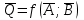 (1.60) (1.60)Для определения поправки Θ вычитаем из (1.59) уравнение (1.60) и усредним левую и правую части полученного выражения: 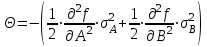 (1.61) (1.61)Видно, что при функциональных преобразованиях результатов измерений, даже при равенстве нулю значений поправок А и В возникает необходимость во внесении поправки Θ. Анализируя (1.61) можно сказать что: 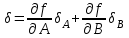 (1.62) (1.62)Переходя к точечным оценкам, получим: 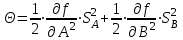 ; (1.63) ; (1.63)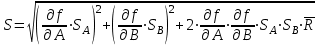 ; (1.64) ; (1.64)где 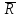 – коэффициент корреляции ( – коэффициент корреляции (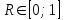 ) )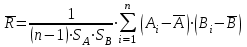 (1.65) (1.65)Рассмотрев общий подход к функциональным преобразования результатов измерений, рассмотрим несколько частных случаев. Пример 1: Алгебраическое сложение результатов измерений. Измеряют сопротивления двух резисторов. Получен результат R1=100 Ом, SR1=5.8 (распределение равномерное) и R2=100 Ом, SR2=5.8 (распределение равномерное). Определить сопротивление последовательно соединенных указанных резисторов. Решение: 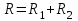 1. Определим 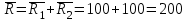 Ом; Θ=0. Ом; Θ=0.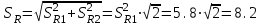 Ом. Ом.2. Определим сопротивление R с учетом того, что R1=R2, как R=2·R1. Тогда 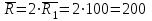 Ом; Ом; 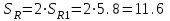 Ом. Ом.Пример указывает на то, что для результатов измерений операция сложения не эквивалентна операции умножения, то есть 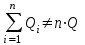 , где Qi=Q. , где Qi=Q.Выше указывалось, что распределение вероятности алгебраической суммы нескольких случайных величин называют композицией их распределений. Полезно знать, что композицией двух равномерных законов распределения является треугольный закон распределения (закон Симпсона). Композицией двух равномерных законов с неодинаковым размахом является трапециидальный закон. С увеличением числа независимых слагаемых композиция их законов распределения быстро стремиться к нормальному закону (4..5 слагаемых). Нормальный закон является наиболее устойчивым. Вернемся к рассмотренному примеру. Определим интервал, в котором лежит значение суммарного сопротивления. Поскольку как установлено закон распределения треугольный, то воспользовавшись…. |
