Беляева математика. 1. 2 0 Вычислить пределы последовательностей Разделим числитель на знаменатель Сделаем замену
 Скачать 96.34 Kb. Скачать 96.34 Kb.
|
|
Задачи: 1. Выполнить деление комплексных чисел  = =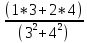 + + i= i=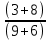 + + i= i=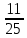 + +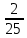 i=0,44+0,08i i=0,44+0,08i1.2  = 0 = 02. Вычислить пределы последовательностей  Разделим числитель на знаменатель  Сделаем замену U= 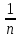 Тогда   = = 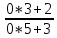 Получаем окончательный ответ  2.2 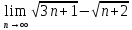 Устраним неопределенность ∞ - ∞ Домножим и разделим 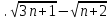 2Тогда 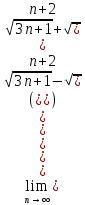  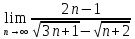 Разделим числитель и знаменатель на sqrt(n):  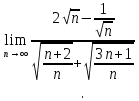  Cделаем замену U = 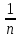 Тогда 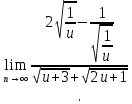 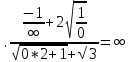 Получаем окончательный эффект 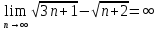 3. Используя признаки Даламбера и Коши исследовать сходимость рядов 3.1  Признак Даламбера.  при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность (дополнительные исследования). 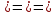 Поскольку q < 1, то ряд сходится. 3.2 Применим радикальный признак Коши:  Поскольку полученное значение меньше 1, то ряд сходится. Поскольку полученное значение меньше 1, то ряд сходится.4. Найти производные сложных функций 4.1 y=sin(lnx) Продифференциуем каждый член по x , затем решим относительно y 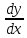 = = 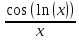 4.2 y= ln 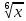 Продифференциуем каждый член по x , затем решим относительно y 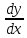 = =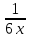 5. Вычислить неопределенный интеграл 5.1 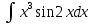 Произведем интегрирование по частям с помощью формулы ∫udv=uv−∫vdu∫udv=uv-∫vdu. 12(−x3cos(2x)+32x2sin(2x)+32xcos(2x)−34sin(2x))+C 5.2 Формула интегрирования по частям: Положим U=x2 dV=2x dx Тогда: dU = 2·x dx Поэтому: Находим интеграл 6. Найти частные производные первого и второго порядка 6.1 z= 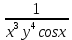 Находим частные производные: При нахождении ∂z/∂x считаем аргумент y постоянным: При нахождении ∂z/∂y считаем аргумент x постоянным: Найдем смешанные частные производные: Для того, чтобы найти ∂2z/∂x∂y дифференцируем ∂z/∂x по у: 6.2 z = 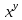 Находим частные производные: При нахождении ∂z/∂x считаем аргумент y постоянным: При нахождении ∂z/∂y считаем аргумент x постоянным: Найдем смешанные частные производные: Для того, чтобы найти ∂2z/∂x∂y дифференцируем ∂z/∂x по у: 7. Найти сумму матриц 7.1A 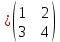 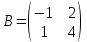 A+B= 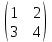 + + 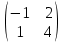 = =  7.2  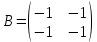 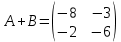 + + 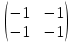 = = 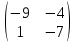 8. Найти произведение матриц A=  B= B=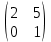 A * B =  * * 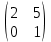 = = 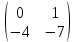 8.2 A=  B = B =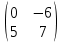 A * B =  * * 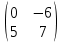 = = 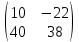 9. Найти опреде лители матриц 9.1 A =  = 3·3 - 2·1 = 9 - 2 = 7 = 3·3 - 2·1 = 9 - 2 = 79.2 A = 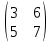 = 3·7 - 5·6 = 21 - 30 = -9 = 3·7 - 5·6 = 21 - 30 = -910.Решить систему уравнений 10.1  Решение методом подстановки:   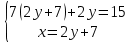   10.2    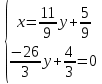 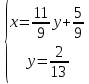  11.Для заданных векторов найти смешанное произведение 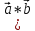 ]* ]*  =(1;-2;1) =(1;-2;1) =(2;1;-2) =(2;1;-2) =(1;1;1) =(1;1;1)1·1·1 + (-2)·(-2)·1 + 1·2·1 - 1·1·1 - (-2)·2·1 - 1·(-2)·1 = 1 + 4 + 2 - 1 + 4 + 2 = 12  =(1;1;2) =(1;1;2) =(1;-1;-3) =(1;-1;-3) =(-2;-2;2) =(-2;-2;2)1·(-1)·2 + 1·(-3)·(-2) + 2·1·(-2) - 2·(-1)·(-2) - 1·1·2 - 1·(-3)·(-2) = -2 + 6 - 4 - 4 - 2 - 6 = -12 |
