математика. 1. Выполнить деление комплексных чисел Деление комплексных чисел определяется как действие, обратное умножению
 Скачать 109.33 Kb. Скачать 109.33 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ Математика Группа Пг19М671 Студент М.М.О.Дадашев МОСКВА 2019 1. Выполнить деление комплексных чисел: Деление комплексных чисел определяется как действие, обратное умножению. 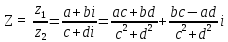 а) 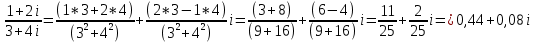 б) 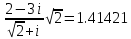 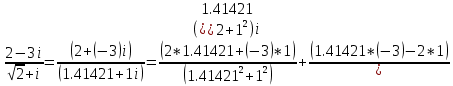 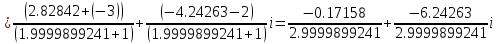 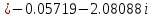 в) 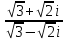 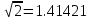 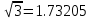 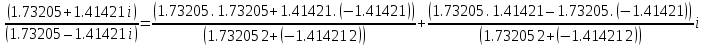 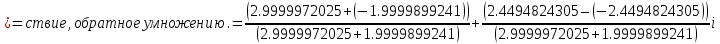 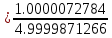 + +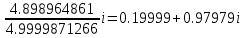 г) 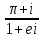 π = 3.14159 ℮= 2.71828 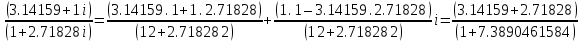 + +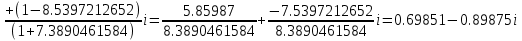 д) 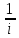 = =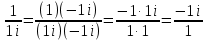 = -1i = -1iе) 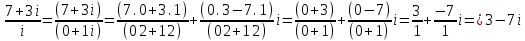  2. Вычислить пределы последовательностей: 2. Вычислить пределы последовательностей:а) 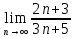 Разделим числитель и знаменатель на n: 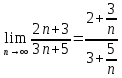 При n→ При n→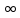 значение каждой из дробей стремится к 0. Получается выражение: значение каждой из дробей стремится к 0. Получается выражение: 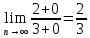 б) 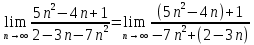 Разделим числитель и знаменатель на 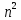 : : 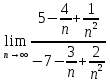 При n→ 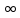 значение каждой из дробей стремится к 0. Получается выражение: значение каждой из дробей стремится к 0. Получается выражение: 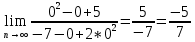 в) 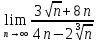 Вычислим с помощью метода Лопиталя. У нас есть неопределенность типа 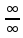 , т.к. предел для числителя , т.к. предел для числителя 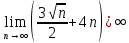 и для знаменателя предел 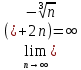 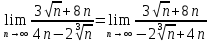 Преобразуем немного функцию под знаком предела 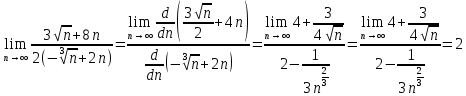 г) 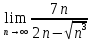 Вычислим с помощью метода Лопиталя. У нас есть неопределенность типа 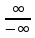 , т.к. предел для числителя , т.к. предел для числителя 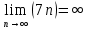 и для знаменателя предел 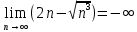 Преобразуем функцию под знаком предела: 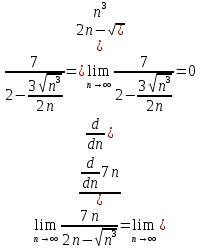 д) 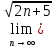 - -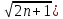 При n 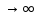 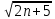 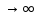 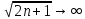 , имеем предопределенность вида , имеем предопределенность вида 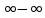 Применим формулу 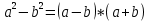 a= 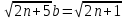 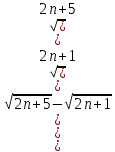 )*( )*(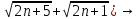 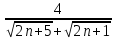 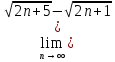 )= )=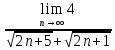 = 0 = 0е) 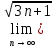 - -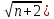 При n 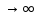 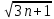 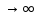 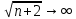 , имеем предопределенность вида , имеем предопределенность вида 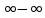 Применим формулу 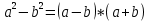 a= 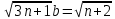 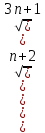 3n+1-n-2=2n-1= 3n+1-n-2=2n-1=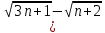 )*( )*(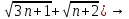 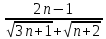 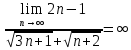 ж) 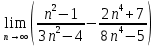 по св-ву вычисления пределов по св-ву вычисления пределов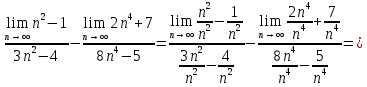 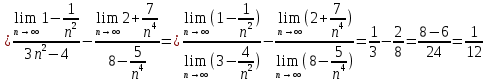 з) 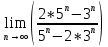 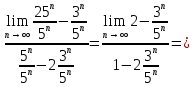 т.к. функция показательная 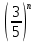 0 0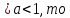 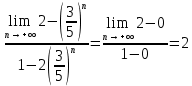 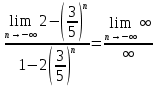 3. Используя признаки Даламбера и Коши исследовать сходимость рядов: а) 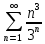 Признак Даламбера. при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность (дополнительные исследования). = = = Поскольку q < 1, то ряд сходится. б) 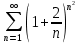 Применим радикальный признак Коши: = Поскольку полученное значение больше или равно 1, то ряд расходится. в) 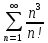 Признак Даламбера. при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность (дополнительные исследования). = = = Поскольку q < 1, то ряд сходится. г) 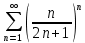 Применим радикальный признак Коши: = Поскольку полученное значение больше или равно 1, то ряд расходится. д) 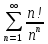 Признак Даламбера. при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность (дополнительные исследования). = = = Поскольку q < 1, то ряд сходится. е) 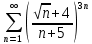 Применим радикальный признак Коши: = Поскольку полученное значение меньше 1, то ряд сходится. 4. Найти производные сложных функций. 1. 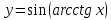 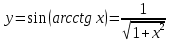 следовательно следовательно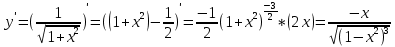 2. 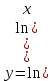 Производная сложной функции 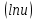 = =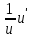 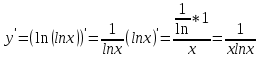 3. 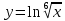 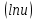 = =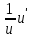 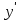 = =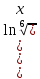 = =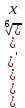 = =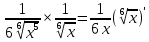 = =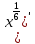 = =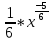 = =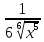 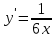 4. 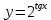 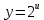 ( (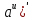 = =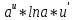 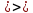 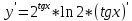 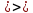 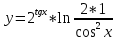 = =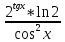 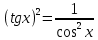 5. 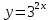 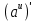 = =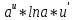 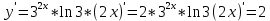 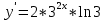 6. 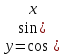 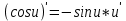 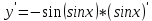 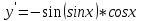 7. 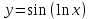 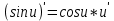 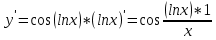 = =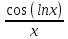 8. 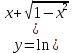 ) )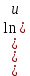 = =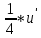 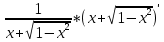 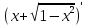 = =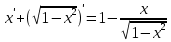 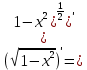 = =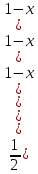 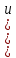 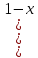 = =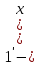 = =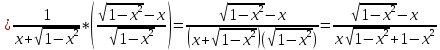 9. 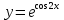 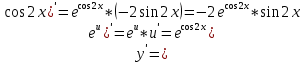 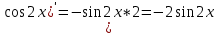 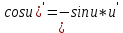 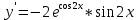 10. 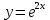 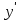 =( =(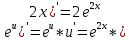 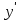 = =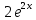 11. 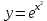 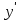 =( =(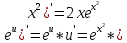 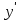 = =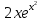 12. 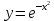 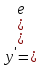 = =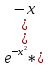 5. Вычислить неопределенный интеграл 1) 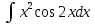 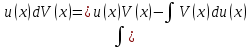 Применим формулу интегрирования по частям 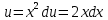 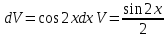 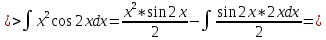 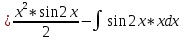 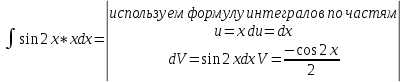 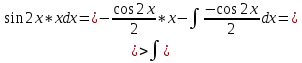 = 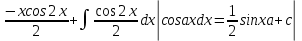 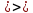 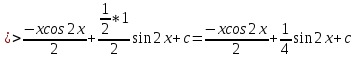 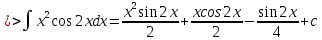 2) 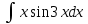 Применим формулу интегрирования по частям 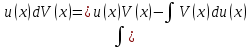 Сделаем замену 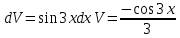 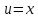 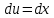  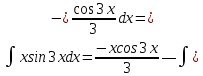 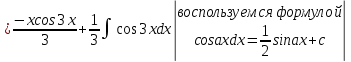 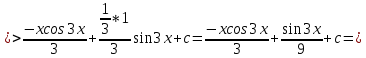 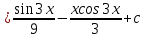 3) 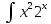 dx dxПрименим формулу интегрирования по частям 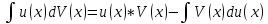 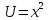 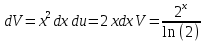 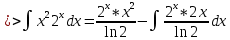 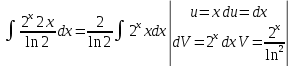 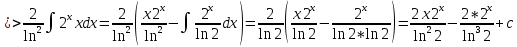 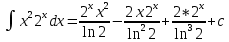 4) 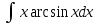 Применим формулу интегрирования по частям 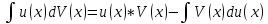 Пусть 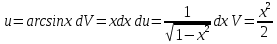 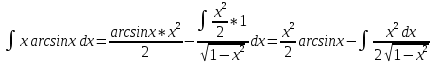 Находим интеграл 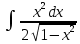 Сделаем замену 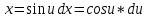 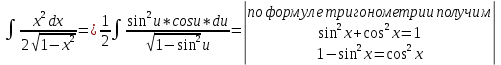 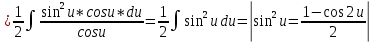 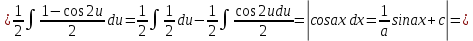 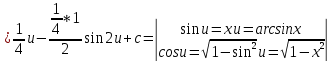 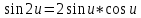 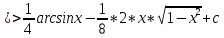 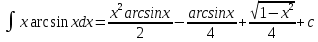 5) 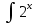 cos 2xdx cos 2xdxПрименим формулу интегрирования по частям 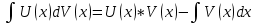 Сделаем замену 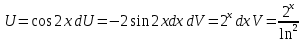 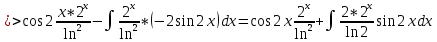 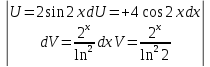 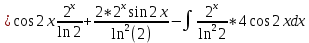 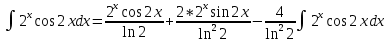 Исходный интеграл повторяется в правой части, т.о можем решить уравнение по 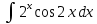 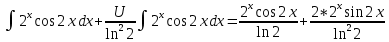 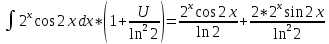 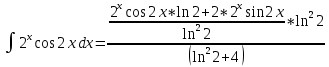 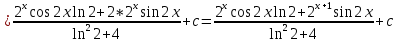 6) 6) 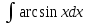 Интегрирование по частям 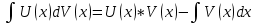 Пусть 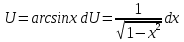 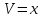 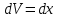 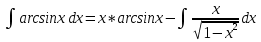 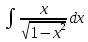 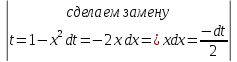 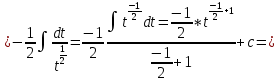 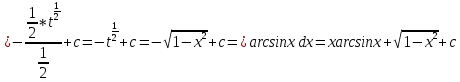 7) 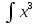 sin 2xdx sin 2xdxПрименим формулу интегрирования по частям 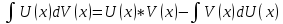 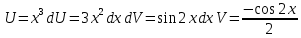 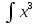 sin 2xdx = sin 2xdx =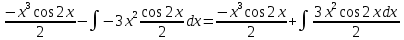 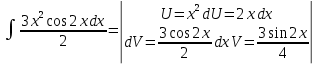 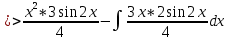 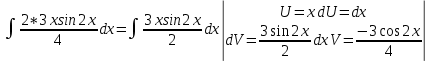 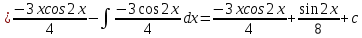 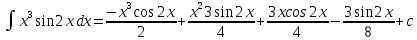 8) 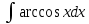 Формула интегрирования по частям 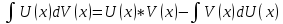 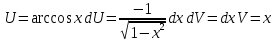 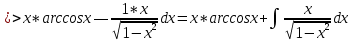 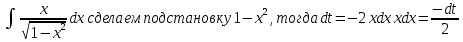 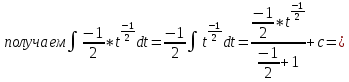 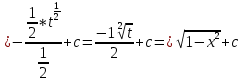 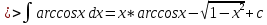 9) 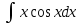 Полагаем U=x dV=cos(x)dx Тогда dU=dx V=sin(x)   6. Найти частные производные первого и второго порядка: 1)   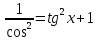 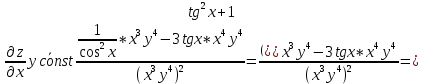 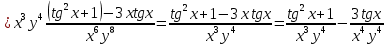 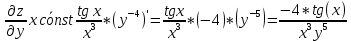 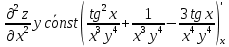 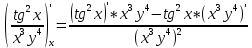 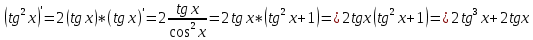 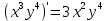 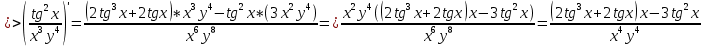 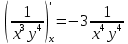 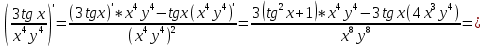 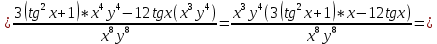 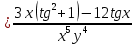 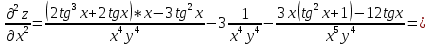 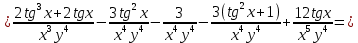 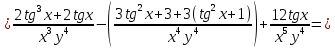 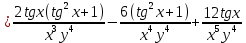 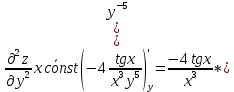 Найдем смешанную производную 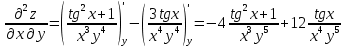 2) 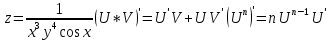 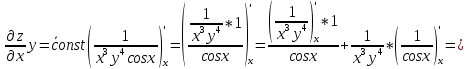 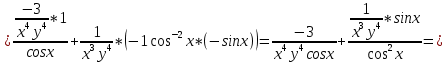 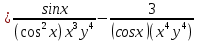 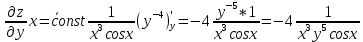 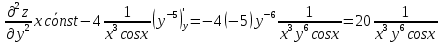 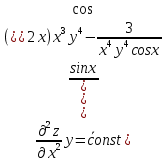 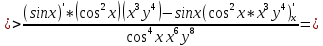 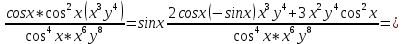 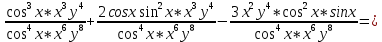 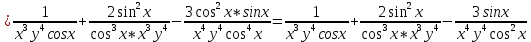 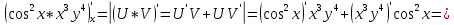 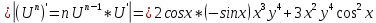 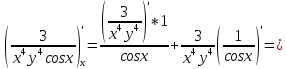 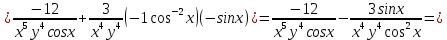 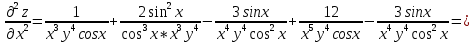 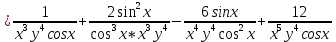 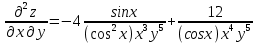 3) 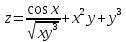 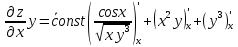 Найдем отдельно каждую производную 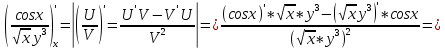 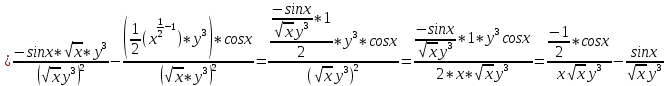 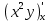 = 2xy = 2xy 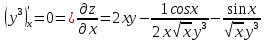 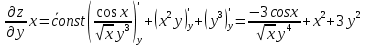 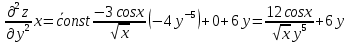 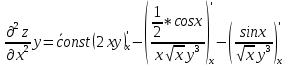 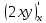 =2y =2y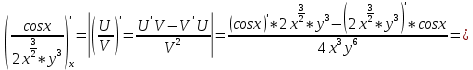 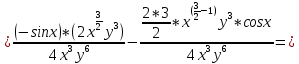 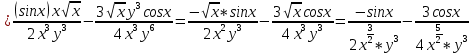 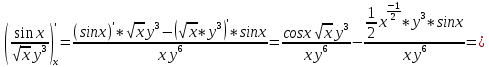 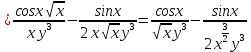 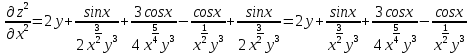 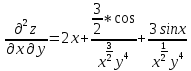 4) 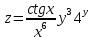 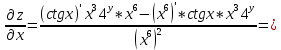 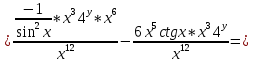 из тригонометрии 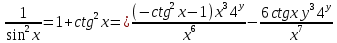 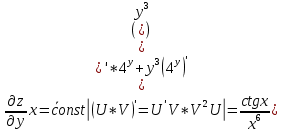 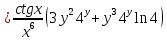 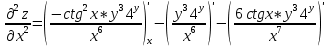 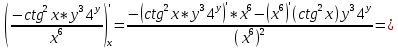 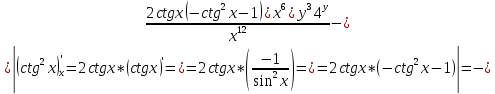 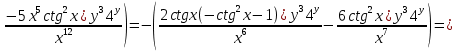 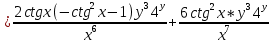 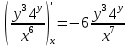 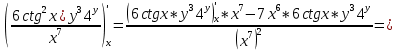 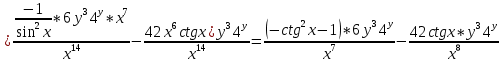 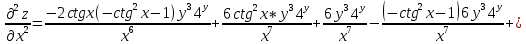 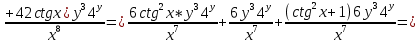 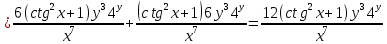 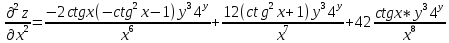 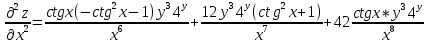 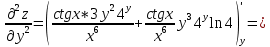 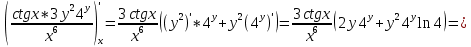 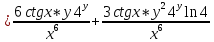 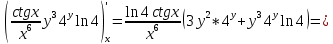 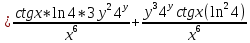 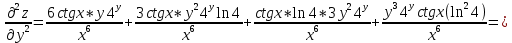 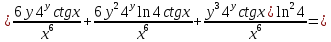 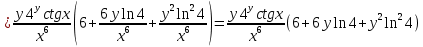 5) 5)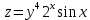 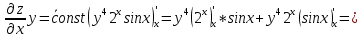 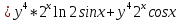 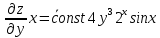 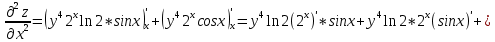 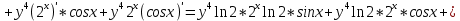 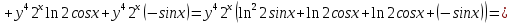 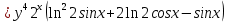 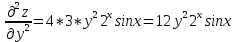 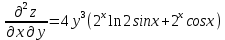 6) 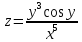 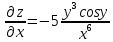 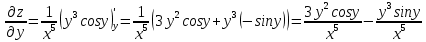 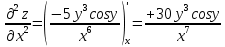 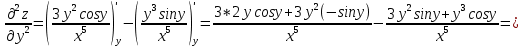 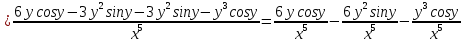 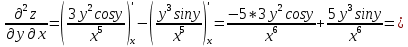 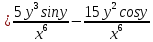 7) 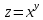 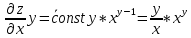 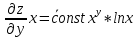 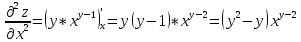 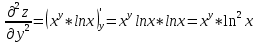 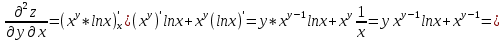 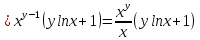 8) 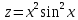 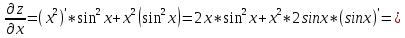 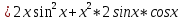 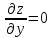 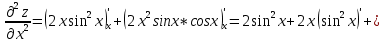 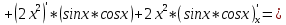 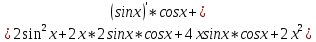 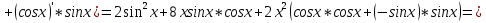 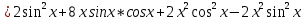 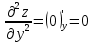 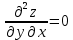 9) 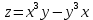 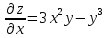 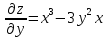 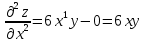 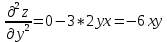 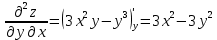 10) 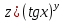 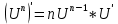 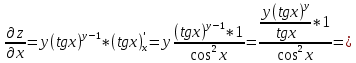 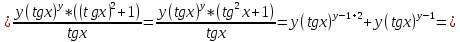 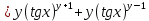 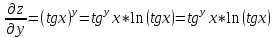 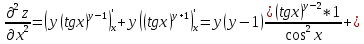 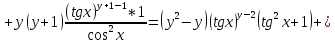 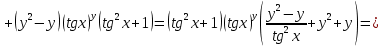 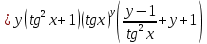 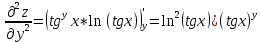 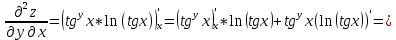 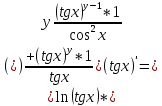 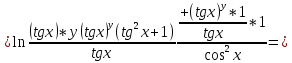 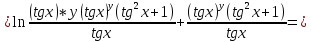 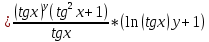 7. Найти: а. Произведение b. Сумму матриц 1. 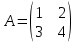 В= В=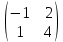 А+В = 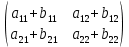 A*B= A*B=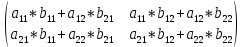 A+B= 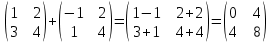 A*B= 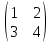 * *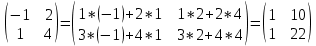 2. A= 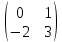 B= B=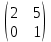 A+B= 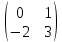 + +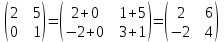 A*B= 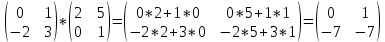 3. A= 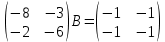 A+B= 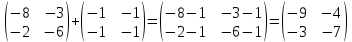 A*B= 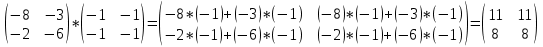 4. A= 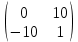 B= B= 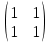 A+B= 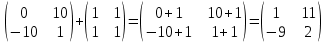 A*B= 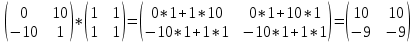 5. 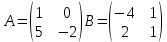 A+B= 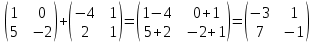 A*B= 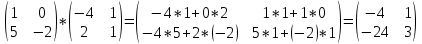 6. A= 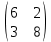 B= B=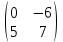 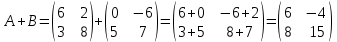 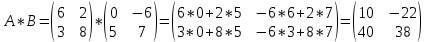 8. Найти определители матриц: Определители матриц 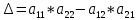 1. 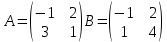 A= 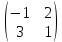 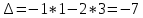 B= 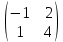 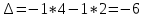 2. A= 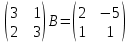 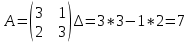 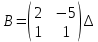 =2*1-(-5)=2+5= 7 =2*1-(-5)=2+5= 7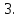 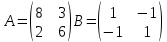 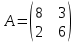 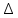 =8*6-2*3=42 =8*6-2*3=42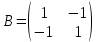 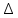 =1*1-(-1)*(-1) = 0 =1*1-(-1)*(-1) = 0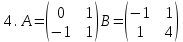 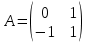 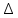 =0*1-(-1)*1=1 =0*1-(-1)*1=1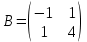 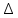 =-1*4-1*1=-5 =-1*4-1*1=-5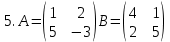 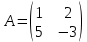 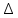 =1*(-3)-5*2= -13 =1*(-3)-5*2= -13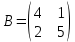 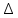 =4*5-2*1=20-2=18 =4*5-2*1=20-2=18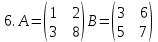 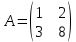 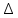 =1*8-2*3=2 =1*8-2*3=2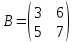 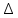 =3*7-5*6=21-30= -9 =3*7-5*6=21-30= -99. Решить систему уравнений: 1. 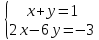 x=1-y x=1-y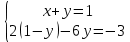 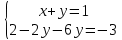 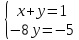 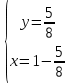 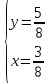 2. 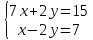 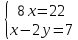 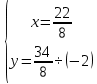 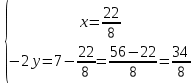 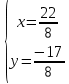 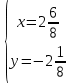 3. 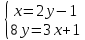 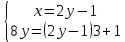 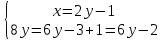 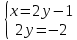 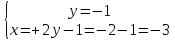 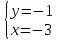 4. 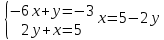 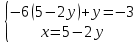 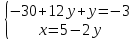 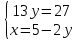 y= y=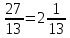 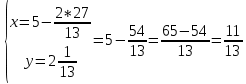 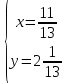 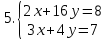 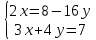 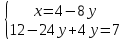 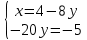 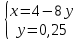 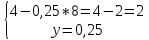 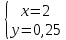 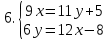 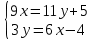 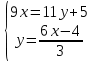 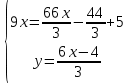 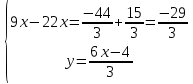 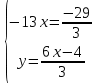 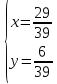 10. Для заданных векторов найти смешанное произведение 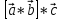 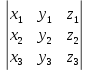 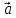 =( =(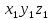 ) ) 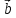 =( =(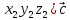 = =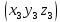 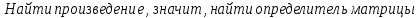 1) 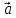 =(1;0;-2), =(1;0;-2), 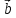 =(2;1;0), =(2;1;0), 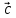 =(-1;1;1) =(-1;1;1)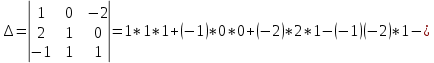 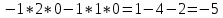  2) 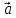 =(1;-2;1), =(1;-2;1), 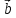 =(2;1;-2), =(2;1;-2), 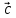 =(1;1;1) =(1;1;1)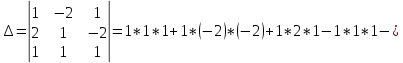 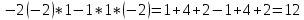 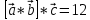 3) 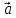 =(1;1;2), =(1;1;2), 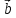 =(1;-1;3), =(1;-1;3), 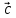 =(-2;-2;2) =(-2;-2;2)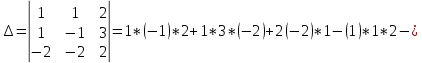 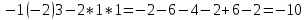 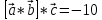 4) 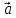 =(1;-1), =(1;-1), 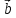 =(2;1), =(2;1), 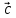 =(-2;-1) =(-2;-1)Смешанное произведение 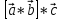 = =   5)  =(1;-2), =(1;-2), 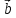 =(2;3), =(2;3), 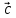 =(-1;1) =(-1;1)Найти смешанное произведение, значит найти определитель матрицы 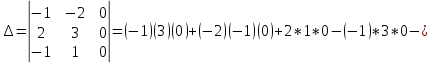 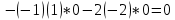 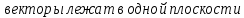 6) 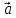 =(3;4), =(3;4), 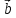 =(4;-1), =(4;-1), 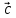 =(1;-1) =(1;-1)Смешанное произведение 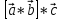 = =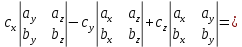 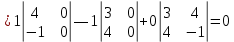 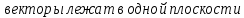 |
