1. 2 Топоцентрические системы координат в геодезии

• Название: 1. 2 Топоцентрические системы координат в геодезии
• Дата: 08.02.2018
• Размер: 0.64 Mb.
• Имя файла: Curs de lectii Geodezie 2, rus.doc
• Тип: Документы; #36117

Tema1: Системы координат, используемые в геодезии (4 ore)

1.1 Геоцентрическая система координат

1.2 Топоцентрические системы координат в геодезии

1.3 Полярная топоцентрическая система координат

1.4 Геодезические датумы

1.5 Преобразования координат

1.1 Геоцентрическая система координат
Координаты – параметры, определяющие положение точек в пространстве и на плоскости.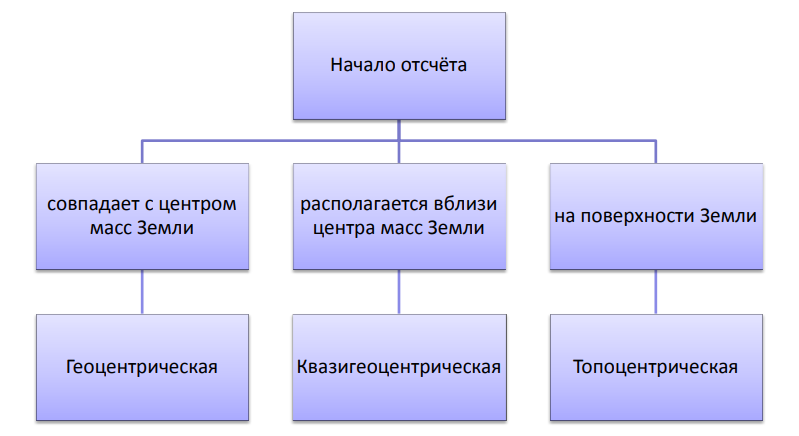



Рис. 1.1 - Классификация систем координат по расположению начала координат

Геодезические координаты со времён древности используются в навигации и картографии. В картографии они являются основой построения проекций.

Системы, начало которых совпадает с центром масс Земли, называют геоцентрическими.

Геоцентрическая система координат необходима для вычисления спутниковых орбит и решения других орбитальных задач.

Проекции, используемые картографами различных стран, основаны на различных геодезических датумах, т.е. созданы на различных эллипсоидах с разными размерами, положением центров и ориентацией осей в пространстве.

Для определения положения точек в геодезии используют прямолинейные прямоугольные (двумерные – на плоскости, трехмерные – в пространстве) системы координат. Указанные системы координат можно классифицировать по следующим основным признакам:

1) По расположению начала отсчета координат – геоцентрические, квазигеоцентрические и топоцентрические;

2) По виду координатных линий – прямоугольные на плоскости и в пространстве, криволинейные (сферические – на шаре, эллипсоидальные – на эллипсоиде);

3) По назначению - звездные и земные.

При решении многих задач геодезии, охватывающих большие пространства, фигура Земли аппроксимируется математически правильной фигурой эллипсоида вращения, близкого к геоиду (квазигеоиду). Эллипсоид вращения, параметры которого подбирают при условии наилучшего соответствия фигуре геоида в пределах всей Земли, называютобщим земным эллипсоидом(Нормальной Землей). В различных странах для обработки геодезических измерений используют эллипсоиды, размеры и ориентирование которых в теле Земли наилучшим образом подходят для данной территории; такие эллипсоиды называютреференц - эллипсоидами.

В геоцентрической системе началом координат является центр масс Земли (рис. 1.1). Ось X имеет направление по Гринвичскому меридиану к экватору. Ось Y располагают в прямоугольном положении на восток от X. Ось Z изначально имеет полярное направление по малой оси эллипсоида.



Рис. 1.1 – Геоцентрическая и топоцентрическая система координат



Рис. 1.2 - Геоцентрическая система координат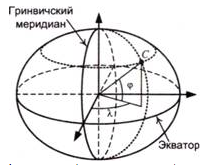



Рис. 1.3 - Географическая (геодезическая) система координат

Однако более привычной является географическая (геодезическая) система координат, когда координаты точки на поверхности эллипсоида определяются широтой φ и долготой λ, измеряемыми в градусах от экватора и от Гринвичского меридиана соответственно (рис. 1.4). Координаты любой точки в пространстве складываются из широты и долготы её проекции по нормали на эллипсоид и высоты Н точки относительно эллипсоида.

В связи с тем, что широта и долгота точки на местности зачастую определяются с помощью астрономических наблюдений, географические координаты также иногда называются астрономическими.

Центр масс Земли, или геоцентр выбирается в качестве начала во многих системах координат, поскольку является очень устойчивой точкой в теле Земли. Эта точка реализуется по наблюдениям спутников, движущихся в гравитационном поле Земли. Геоцентр рекомендован в качестве начала для земной референцной системы как центр масс Земли включая океаны и атмосферу.

Анализ спутниковых лазерных дальномерных наблюдений уверенно показывает, что система отсчёта, реализованная в координатах станций наблюдений, неподвижных относительно земной коры, ощутимо смещается относительно центра масс Земли.

В 1997 г. Международная служба вращения Земли (МСВЗ) провела кампанию по исследованию стабильности геоцентра, в которой приняли участие 42 исследователя из 25 научных групп, использовавших современные геофизические модели и результаты лазерных измерений, GPS и DORIS. В конце 1997 г. в Сан-Франциско состоялась встреча по обмену результатами работы. Величина вековых движений в компонентах координат геоцентра составляет:

– 0.801 см/столетие, 0.177 см/столетие, 0.214 см/столетие.

Вековые смещения в положении геоцентра можно объяснить такими причинами:

• 
  Изменение уровня моря.
  
• 
  Изменения в ледяном щите (в Гренландии, Антарктиде).
  
• 
  Тектонические смещения в земной коре (постледниковая отдача, движение тектонических плит, субдукция и др.).
  

По результатам обработки реальных наблюдений выявлены годовые колебания в положении геоцентра (амплитуда около 4 мм по координатам Х, У и порядка 10 мм по Z), полугодовые с периодами около 140 суток, 60-70 суток, 20 суток и 14 суток с амплитудами несколько миллиметров и с погрешностями амплитуд почти такого же порядка.

Общее мнение участников встречи таково, что движение отсчётной наземной сети относительно геоцентра поддаётся выявлению, но величина его небольшая, вероятно, не более 1 см по каждому из компонент. Учитывать изменения положения геоцентра в результатах измерений пока не рекомендовано.

Земные геоцентрические системы реализуются в виде геодезических сетей, построенных методами космической геодезии (или с обязательным применением методов космической геодезии). Пункты таких сетей распределены по всему земному шару или по значительной его части. Чем более точны положения этих точек, тем меньше остаточные ошибки, и более точна реализация координатной системы.

В понятие земной геоцентрической системы входят не только координаты пунктов, которые закрепляют данную систему на местности, но и ряд других параметров, характеризующих её. В первую очередь это параметры земного эллипсоида, определяющие размеры и форму Земли. Для построения эллипсоида используют два главных параметра: экваториальный радиус а и сжатие α. Остальные параметры, определяющие размеры и форму эллипсоида можно вычислить по этим двум параметрам.

Из других параметров нужно указать параметры, представляющие гравитационное поле Земли, параметры связи с другими системами координат, число которых может достигать многих тысяч. Поэтому, когда говорят о современной геоцентрической системе координат (или системе отсчёта) подразумевается система геодезических параметров Земли.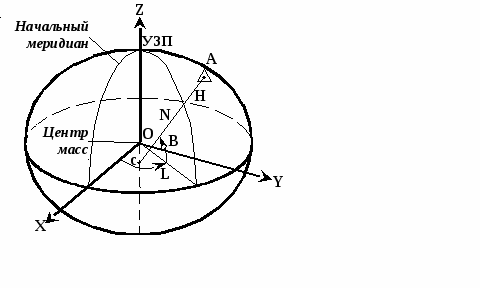



Рис. 1.4 - Геоцентрическая система координат

Все геоцентрические системы связаны с определёнными эллипсоидами, названия которых обычно совпадают с названием самой системы. В этом случае возможно использование не только декартовых, но и эллипсоидальных (сфероидических) координат: геодезической широты В, геодезической долготы L и высоты над эллипсоидом Н. Для определения геодезических координат из точки А проводится нормаль к эллипсоиду АС. Геодезической широтой В называют угол между нормалью и плоскостью экватора эллипсоида, а геодезической долготой L – угол, отсчитываемый против часовой стрелки от начального меридиана до меридиана пункта. Прямоугольные координаты Х,У,Z вычисляются по геодезическим координатам В, L, Н по формулам:

(1.1)

где радиус кривизны эллипсоида в первом вертикале, определяемый как

(1.2)

При переходе от прямоугольных координат к геодезическим определение долготы не вызывает затруднений:

(1.3)

а определение широты возможно несколькими способами. Их делят на итеративные и замкнутые. Из алгоритмов первой группы приведём метод, в котором геодезическая широта В находится по формуле:

(1.4)

где номер итерации, повторяющейся до тех пор, пока (точность вычислений); проекция радиус-вектора на плоскость экватора:



а величина 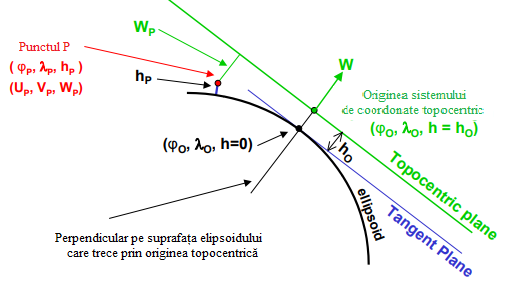находится из предыдущего приближения. Эллипсоидальная высота Н определяется по формуле:





Figura 1.2 – Altitudinile topocentrice și elipsoidale

Топоцентрические координаты [U, V, W] вычисляются со следующими соотношениями, следующим образом:

(1.8)

где:

(1.9)

Или, выраженные в виде скалярных уравнений: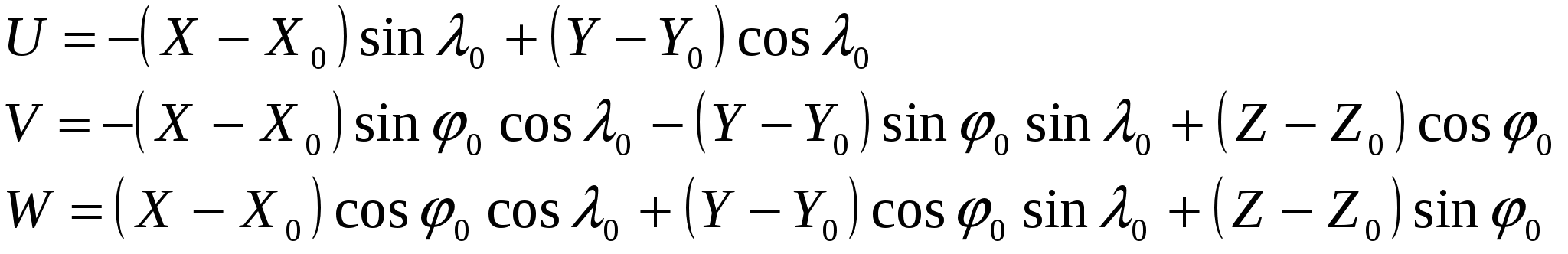

(1.10)

Обратные формулы для вычисления геоцентрических координат из топоцентрических координат: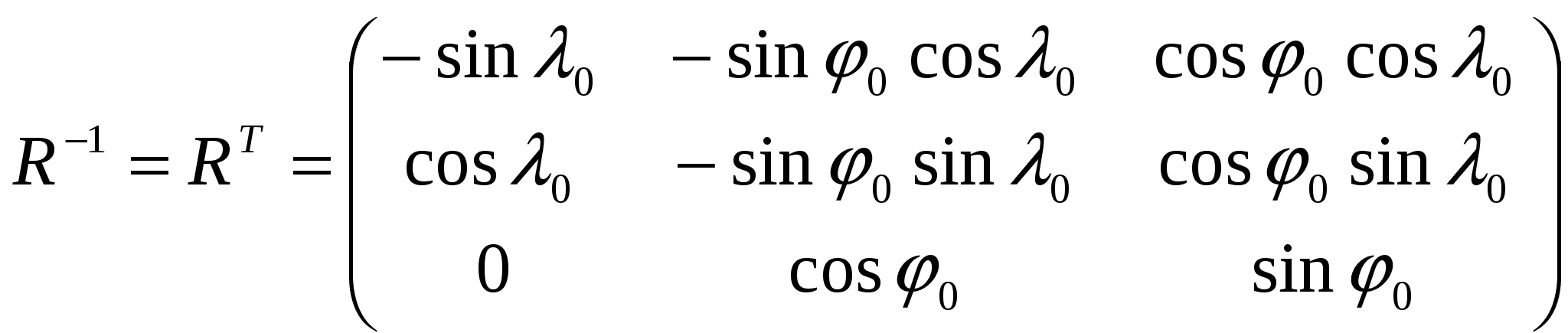

(1.11)

Или, выраженные в виде скалярных уравнений:

(1.12)

Rэто матрица вращения, объединяющая три вращения вокруг соответствующих осей X, Y и Z.

Глобальной геоцентрической декартовой системой считается основная система геодезии. Декартовые координаты X, Y, Z, полученные в геодезии со спутниками, определяют положение точки P, расположенной на физической поверхности Земли.

Положение точки P также может быть определено другими глобальными координатами, а именно астрономическими координатами  и , (астрономическая широта и долгота), заполненными ортометрической высотой H^OR. Эти координаты будут называться глобальными астрономическими координатами.

Астрономические координаты Φ и  определяют положение вертикали в рассматриваемой точке. Поэтому, как только основная ось любого геодезического инструмента оказывается вертикально, геодезические наблюдения попадают в естественную систему отсчета.

1.2 Топоцентрические системы координат в геодезии

Использование вышеприведённых геоцентрической и географической систем координат не всегда удобно. Так, при работе на небльших участках земной поверхности чаше применяется топоцентрическая (горизонтная) система координат, которая является обычной прямоугольной пространственной системой координат

Топоцентрическая система координат — естественная система для работы различных наземных объектов: ракетных стартовых комплексов, станций слежения за спутниками, станций ПВО и других измерительных комплексов. Естественно, собираемая информация в каждом случае преобразуется в общую систему координат, связанную с Землёй — геодезическую систему координат.

Внастоящее время в геодезической практике широкое распространение получили пространственные топоцентрические СК. Это такие системы, начало отсчета которых находится в некоторой точке наблюдений Q₀(рис. 1.1) на земной поверхности, под землей или в воздушном пространстве.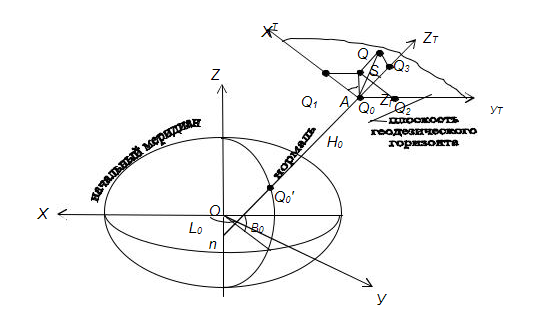



Рис. 1.5 - Топоцентрическая геодезическая СК

Различают топоцентрические прямоугольные и полярные координаты. В зависимости от выбора основной координатной плоскости (плоскости параллельной плоскости земного экватора или плоскости горизонта) топоцентрические СК могут быть либо экваториальными, либо горизонтными.

В геодезии используются, в основном, горизонтные пространственные топоцентрические СК. Пространственная топоцентрическая СК будет геодезической (рис. 1.1), если ось OZ^Tбудет совпадать с нормалью к поверхности эллипсоида в точкеQ₀. Если же ось OZ^Tбудет направлена по отвесной линии в точкеQ₀, то такая топоцентрическая СК будет называться астрономической и ее основной плоскостью будет плоскость астрономического горизонта. На рис. 1.5 приведена пространственная топоцентрическая горизонтная геодезическая (левая) СК.

В этой системе ось OZ^T направлена по нормали к поверхности эллипсоида, ось OХ^Tлежит на пересечении плоскостей геодезического горизонта и геодезического меридиана точки Q₀и направлена на север, ось OУ^Tвыбирается в плоскости геодезического горизонта и дополняет левую декартову СК.

Положение произвольной точки Qв этой СК будет определяться тремя величинами:

Х^Т= Q₀Q₁;

У^Т= Q₀Q₂;

Z^Т= Q₀Q₃.

Пространственные горизонтные топоцентрические СК имеют очень тесную и простую связь с пространственной полярной системой сферических координат точки Q S, Z_г, A(рис. 1.5).

Экваториальные системы пространственных прямоугольных топоцентрических координат отличаются от горизонтных только тем, что их оси выбираются в точке Q₀параллельными осям геоцентрических пространственных прямоугольных СК Х, У, Z, а основной плоскостью является плоскость параллельная плоскости земного экватора, содержащая точкуQ₀.

Начало топоцентрической системы находится в некоторой точке наблюдений А, а оси параллельны осям соответствующих геоцентрических координатных систем. Следовательно, можно образовать истинную небесную топоцентрическую систему , среднюю небесную топоцентрическую систему на эпоху t – , общеземную топоцентрическую систему AX'Y'Z' и другие. С помощью таких координат задается взаимное положение пунктов. Связь между этими системами выражается теми же формулами, что и между геоцентрическими системами.

Очень часто при построении геодезических сетей спутниковыми методами применяются локальные геодезические координаты, основной плоскостью которых является плоскость геодезического горизонта, ось U направлена в геодезический зенит пункта, ось N – на север, а ось Е – на восток (рис. 1.6). Связь координат ENU с топоцентрическими X'Y'Z' определяется формулой: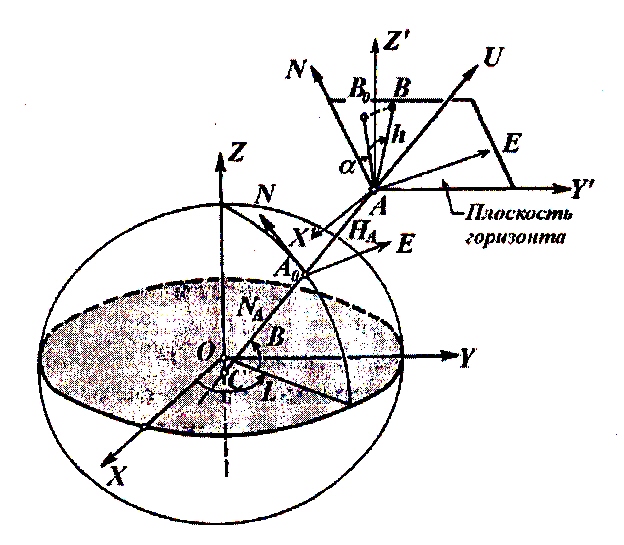

. (5.37)



Рис. 1.6 - Система локальных координат NEU
Матрица R выражается через геодезические координаты пункта А: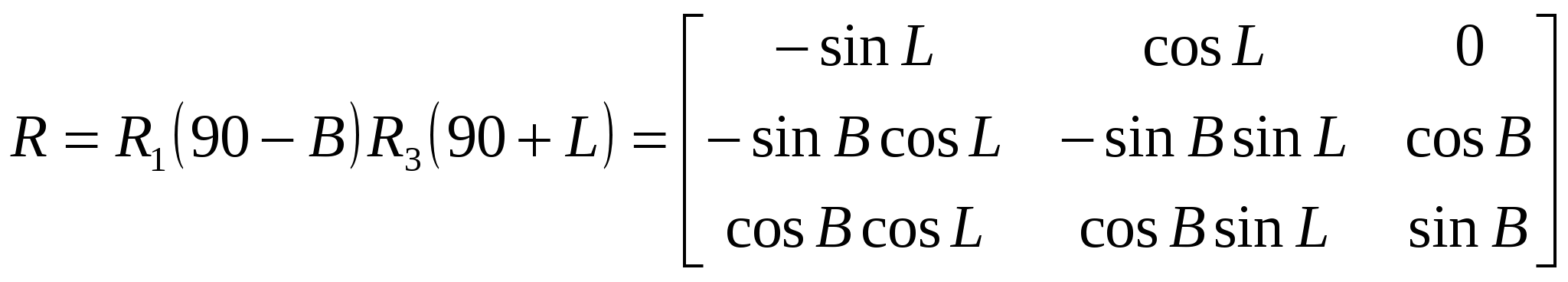

. (1.)

Сферическими координатами пункта В в данной системе являются: геодезический азимут α и геодезическая высота над горизонтом h:

. (1.)

Очевидно, что координаты Е, N, U с пункта А и В и с пункта В и А различаются не только по знаку, но и по величине.
1.3 Полярная топоцентрическая система координат

В противоположность географической системе координат, охватывающих всю Землю, полярная система координат применяется при составлении карт и планов небольших участков.

Положение точки в полярной системе координат определяется относительно некоторой точки, именуемой полюсом О, и полярной оси Ох. Точка N соединяется с полюсом О радиусом - вектором ρ, угол между которым и полярной осью Ох называется углом положения θ.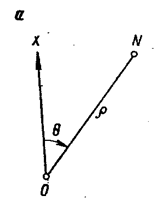



Радиус - вектор ρ и угол положения θ являются полярными координатами точки N. Этих двух величин вполне достаточно для определения положения данной точки. Радиусы - векторы измеряются в метрах, а углы положения, отсчитываются по ходу часовой стрелки, в градусах от 0 º до 360 º

До недавнего времени непосредственно в геодезии применялись поверхностные системы полярных координат: на плоскости, сфере и, особенно, на эллипсоиде. Это было связано с тем, что раньше решение чисто геодезических задач сводилось, в основном, к вычислению координат точек земной поверхности.

В настоящее время, в связи с выходом человека в космос, появлением более высокоточных приборов для измерения полярных координат возникла необходимость в решении задач по определению координат точек в других системах не только непосредственно на поверхности Земли, но и в околоземном пространстве. В этом случае и в геодезии возникла необходимость использования пространственных, сферических, сфероидических полярных систем координат.

Отличительной особенностью использования в геодезии системы пространственных полярных геодезических координат является то, что ее основная плоскость выбирается на поверхности и представляет собой плоскость геодезического горизонта (или параллельная плоскости горизонта). За полярную ось принимается линия пересечения плоскости горизонта с плоскостью геодезического меридиана данной точки О (полюса системы) с положительным направлением на северный полюс Земли.

Положение точки Q в этой СК определяется тремя величинами (координатами): S – длина прямой OQ; А – геодезический азимут (двугранный угол между плоскостью геодезического меридиана начальной точки Ои нормальной плоскостью точки О, содержащей точку Q); Z_г – зенитное расстояние (угол между нормалью точки Ои линией OQ).

При выполнении съемочных и разбивочных геодезических работ часто применяют полярную систему координат (рис.1.7). Она состоит из полюса О и полярной оси ОР, в качестве которых принимается прямая с известным началом и направлением.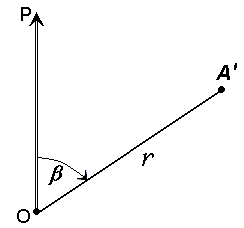



Рис. 1.7 - Полярная система координат

Для определения положения точек в данной системе используют линейно-угловые координаты: угол β, отсчитываемый по часовой стрелке от полярной оси ОР до направления на горизонтальную проекцию точки А', и полярное расстояние r от полюса системы О до проекции А'.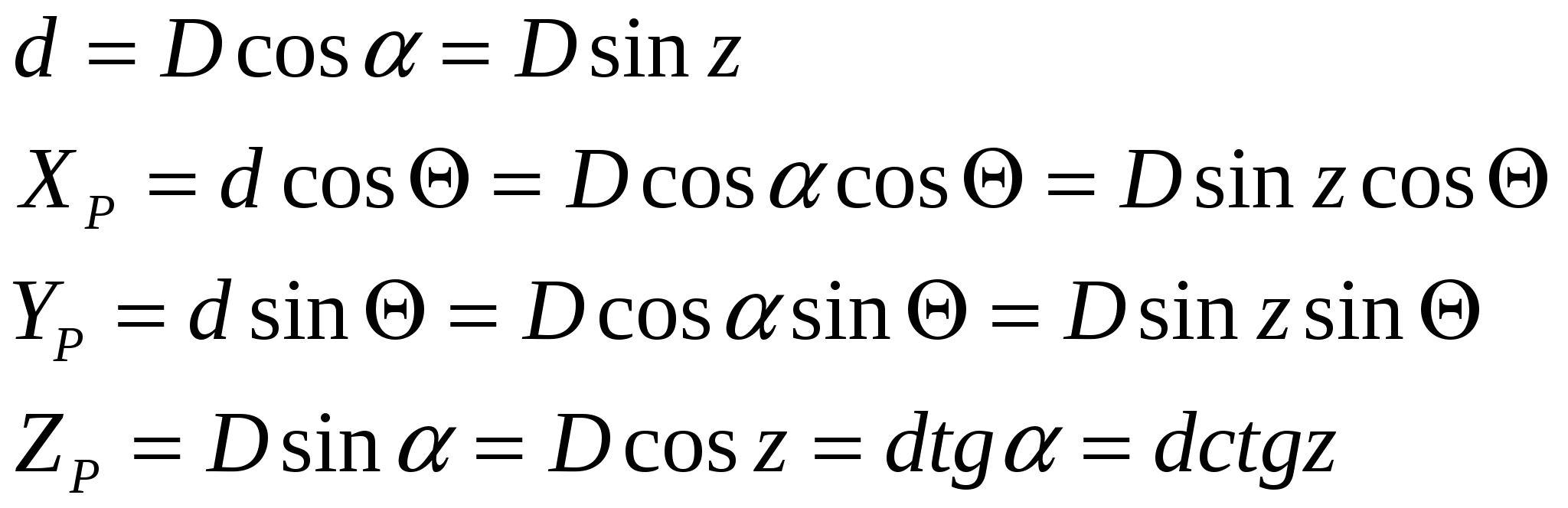



Откуда находим, что: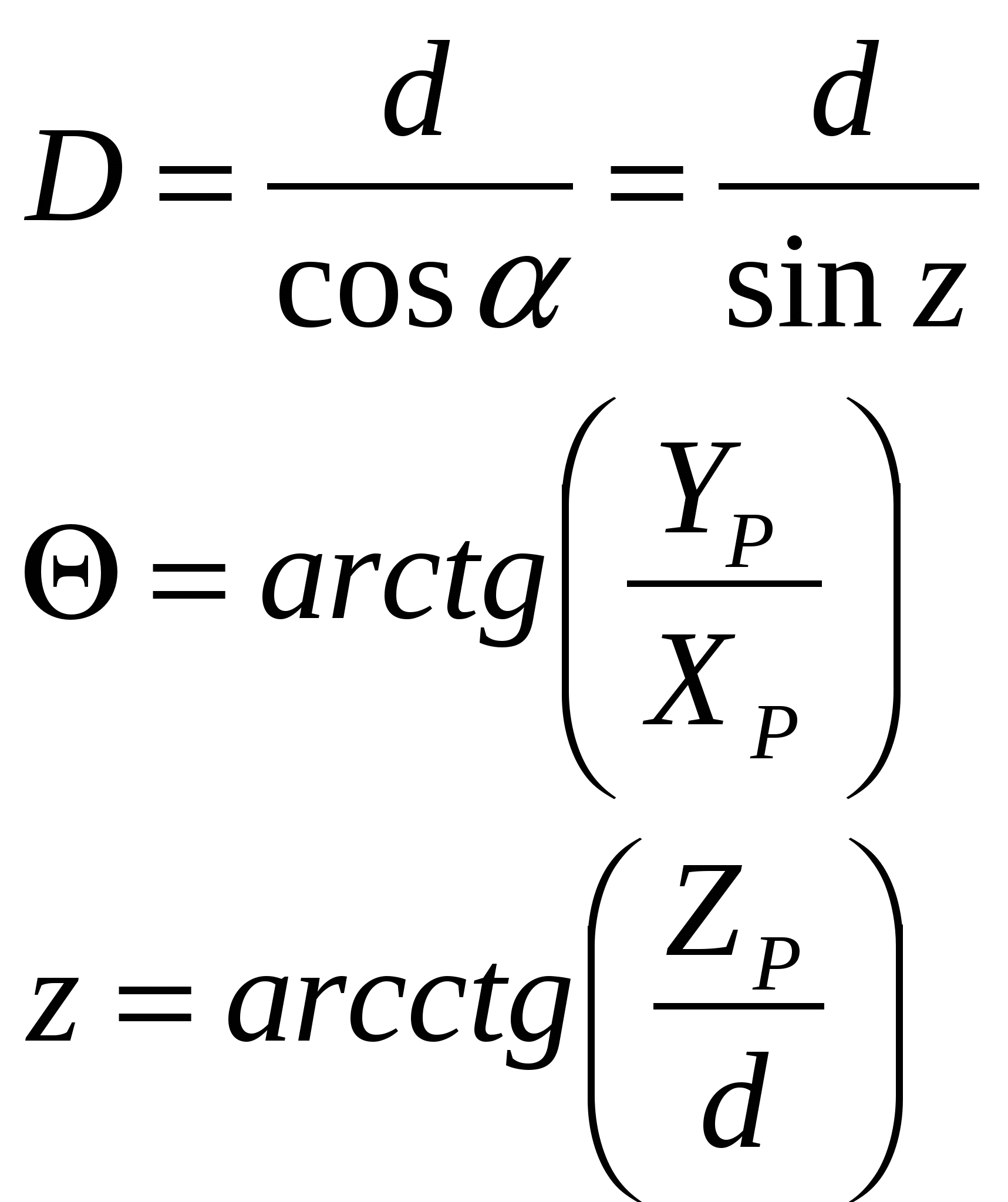


1.4 Геодезические датумы
Датум (лат. Datum) — набор параметров, используемых для смещения и трансформации референц-эллипсоида в локальные географические координаты.

Понятие «Датум» используется в геодезии и картографии для наилучшей аппроксимации к геоиду в данном месте. Датум задается смещением референц-эллипсоида по осям: X, Y, Z, а также поворотом декартовой системы координат в плоскости осей на угол r_X, r_Y, r_Z. Также необходимо знать параметры референц-эллипсоида а и f, где а — размер большой полуоси, f — сжатие эллипсоида.

Чаще всего с датумами приходится сталкиваться в GPS-приемниках, в ГИС-системах и в картографии при использовании какой-либо локальной координатной сети. Преобразование координат в таких системах из одного датума в другой может, в общем случае, выполняться автоматически. Неверная установка датума (либо неправильное его преобразование) в итоге дает горизонтальные и вертикальные ошибки определения места величиной от нескольких до сотни и даже больше метров.

Из самых известных датумов можно выделить геоцентрический датум WGS84. Обычно все данные, полученные приёмниками GPS пересчитываются именно в этот датум. В свою очередь карты были созданы в другом датуме. Он называется Пулково 42. Разница между точками с одинаковыми координатами, но приведёнными в этих двух датумах составляет от 10 до 150м. В других датумах это значение может быть значительно больше. Координаты одной точки на поверхности Земли, указанные в разных датумах, в любом случае описывают одно и то же место. Поэтому имея координаты какой-либо точки на поверхности Земли необходимо знать к каком датуме они были зафиксированы. Иначе возможна ошибка. Тоже самое необходимо помнить и при обмене данными в электронном виде. Далее, в процессе создания карт, мы будем иметь дело только с датумом WGS84.

Общеземная система координат – глобальная геодезическая система WGS-84 (World Geodetic System 1984) с параметрами:

эллипсоид – WGS 84;

большая полуось эллипсоида а = 6 378 137.0 м;

сжатие эллипсоида f = 1:298.257 223 563;

геоцентрическая гравитационная постоянная GM = 3 986 004.418×10⁸ м³с^-2;

нормализованный зональный гармонический коэффициент геопотенциала второго порядка С_2,0= - 0.484 166 774 985×10^-3;

угловая скорость вращения Земли w=7 292 115×10^-11рад c^-1.

Европейская геодезическая референцная система ETRS 89 (European Terrestrial Reference System 1989) с параметрами:

эллипсоид GRS 80

большая полуось эллипсоида а = 6 378 137.0 м;

сжатие эллипсоида f = 1:298.257 222 101;

геоцентрическая гравитационная постоянная GM = 3 986 005×10⁸ м³с^-2;

зональный гармонический коэффициент геопотенциала второго порядка J₂ = 108 263×10^-8;

угловая скорость вращения Земли w=7 292 115×10^-11рад c^-1.

В целях мелкомасштабного картографирования плоские прямоугольные координаты x (N), y (E) вычисляются в универсальной трансверсальной проекции Меркатора UTM (Universal Transversal Mercator) в шестиградусных зонах. Осевыми меридианами шестиградусных зон являются меридианы с долготами 27°, 33° с масштабным коэффициентом k = 0.9996.

Началом координат в каждой зоне является точка пересечения осевого меридиана с экватором. Значение ординаты на осевом меридиане принимается величиной 500 000 м.

Для осуществления топографических и кадастровых съемок в масштабах 1:10 000 и крупнее плоские прямоугольные координаты x (N), y (E) вычисляются в трансверсальной проекции Меркатора в одной на всю территорию Республики Молдова зоне со следующими параметрами:

- геодезическая долгота осевого меридиана: Lo = 2824;

- масштабный коэффициент на осевом меридиане: ko = 0.99994;

- условная абсцисса: xo = -5 000 000 м;

- условная ордината: yo = 200 000 м.

Для удобства пользования проекция с указанными параметрами принимает название Трансверсальная проекция Меркатора для Молдовы (TMM).

За референцную систему координат принимается европейская геодезическая референцная система ETRS 89 (European Terrestrial Reference System 1989.

Система координат с указанными параметрами в проекции TMM с координатами пунктов Национальной геодезической сети, определенными в GPS кампании 1999 года, принимает название MOLDREF 99.

1.5 Преобразования координат

Преобразованием системы координат называется переход от одной системы координат к другой. При такой замене надо установить формулы, позволяющие по известным координатам точки в одной системе координат определить ее координаты в другой.

Координаты точки, полученные с помощью системы GPS, относятся к общеземной системе координат WGS-84 и определяются соответствующей системой исходных геодезических дат. Однако, на конкретной территории, в данной стране или в группе стран уже существуют геодезические сети. Они созданы наземными методами, обработаны в системе конкретного референц-эллипсоида и использованы в качестве основы для выполнения всех геодезических, картографических и других работ на данной территории. Чтобы данные, полученные в двух разных системах, были сравнимы, чтобы их можно было обрабатывать совместно и чтобы можно было использовать данные GPS для решения геодезических задач в референцной системе координат, необходимо выполнить преобразование исходных геодезических дат. Для этого, во-первых, требуется определить местоположение центра референц-эллипсоида относительно начала координат в системе спутниковых геодезических дат. Другими словами, необходимо знать три координаты центра референц-эллипсоида в общеземной системе, которые называют также параметрами параллельного переноса. Кроме того, оси двух эллипсоидов, как правило, непараллельны. Поэтому, во-вторых, бывает необходимо выполнить поворот вокруг осей одной из систем так, чтобы оси обеих систем координат стали бы параллельными. В третьих, необходимо учесть возможную разницу масштабов сетей, создаваемых различными методами и средствами измерений. Принято учитывать это различие введением коэффициента (1+m), где m - параметр, учитывающий отклонение масштаба измерений от единицы.

Таким образом, имеется семь параметров преобразования: три параметра параллельного переноса X₀, Y₀, Z₀; три малых угла поворота вокруг соответствующих координатных осей W_x, W_y, W_z и масштабный коэффициент (1+m), либо просто параметр m, учитывающий отклонение этого коэффициента от единицы. Для того, чтобы перевести геоцентрический вектор ­ R пункта в вектор ­ R_r того же пункта, отнесенный к референцной системе, используется выражение: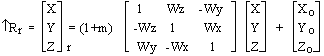



Иногда параметры преобразования определяются национальными геодезическими службами. В противном случае пользователь должен определять их самостоятельно. Это делают, устанавливая приемоиндикаторы на пунктах сети, координаты которых уже известны в референцной системе. Таких пунктов должно быть как минимум три и они должны располагаться по границам территории. Два набора координат - в референцной системе и в общеземной используют затем для определения параметров преобразования, используя метод наименьших квадратов. Настоятельно не рекомендуется использовать полученные таким образом параметры преобразования для пересчета координат пунктов, расположенных вне данной территории, то есть экстраполировать результаты определения параметров преобразования. При работе на небольших участках ограничиваются определением лишь трех параметров параллельного переноса и, иногда, масштабного коэффициента. Параметры вращения в этом случае сильно коррелируют с остальными параметрами, поэтому определять их нецелесообразно. Проблема, возникающая при реализации описанной процедуры заключается в том, что точность существующих сетей, созданных наземными методами, примерно на порядок ниже точности, обеспечиваемой спутниковыми системами.

Если к обеим координатам (абсциссе и ординате) каждой из всех четырех систем координат (географической, полярной, плоской, прямоугольной и зональной) прибавить третью отметку - линейную величину, характеризующую положение точки в третьем измерении (по высоте), они превратятся в пространственные системы координат, которые в основном и применяются в геодезии.


Рис. 1.3 - Геометрическое представление преобразования координат

Sursa:

1. http://www.geogr.msu.ru/cafedra/karta/docs/GOK/gok_lecture_6.pdf

3. http://gis-lab.info/qa/datum-transform-methods.html

4. http://www.epsg.org/Portals/0/373-07-2.pdf

ИНСТРУКЦИЯ по созданию национальной геодезической сети

ПОЛОЖЕНИЕ о переходе на общеземную и референцную системы координат и соответствующие картографические проекции

www.liekc.info/Введение_в_геодезию_Лекция_2

2. Важность теории ошибок в геодезических измерений (2 ore)

2.1. Общие понятия

2.2 Классификация ошибок измерений

2.3 Классификация измерений

2.4 Свойства случайных ошибок

2.5 Метод наименьших квадратов

2.1. Общие понятия
Процесс измерений протекает во времени и определенных условиях, в нём участвуют объект измерения, измерительный прибор, наблюдатель и среда, в которой выполняют измерения. В связи с этим на результаты измерений влияют качество измерительных приборов, квалификация наблюдателя, состояние измеряемого объекта и изменения среды во времени. При многократном измерении одной и той же величины из-за влияния перечисленных факторов результаты измерений могут отличаться друг от друга и не совпадать со значением измеряемой величины. Разность между результатом измерения и действительным значением измеряемой величины называется ошибкой результата измерения.

2.2 Классификация ошибок измерений
По характеру и свойствам ошибки подразделяют на:

• 
  грубые;
  
• 
  систематические;
  
• 
  случайные.
  

Грубые ошибки или просчеты легко обнаружить при повторных измерениях или при внимательном отношении к измерениям.

Систематические ошибки – те, которые действуют по определенным законам и сохраняют один и тот же знак. Систематические ошибки можно учесть в результатах измерений, если найти функциональную зависимость и с её помощью исключить ошибку или уменьшить её до малой величины.

Случайные ошибки – результат действия нескольких причин. Величина случайной ошибки зависит от того, кто измеряет, каким методом и в каких условиях.

Случайными эти ошибки называются потому, что каждый из факторов действует случайно. Их нельзя устранить, но уменьшить влияние можно увеличением числа измерений.


2.3 Классификация измерений
Сравнение какой-либо величины с другой однородной величиной, принятой за единицу, называют измерением, а полученное при этом числовое значение –результатом измерения.

Различают измерения прямые (непосредственные) и косвенные. Основное уравнение прямого измерения

λ = N*K

где λ – результат измерения; К– значение величины, принятой за единицу измерения (сравнение); N – отвлеченное число, показывающее во сколько раз λ больше N.

Косвенные измерения – такие измерения, которые получают по формулам, связывающим значения измеренных физических величин со значениями других физических величин, полученных из прямых измерений и являющихся аргументами этих формул.


2.4 Свойства случайных ошибок

2.5 Метод наименьших квадратов

Библиография

http://ru.calameo.com/read/0017344954fc3ccc4e821

Tema 12. Proiectarea și materializarea pe teren a rețelelor geodezice de îndesire (4 ore)

12.1 Poziționarea rețelelor geodezice

12.2 Clasificarea rețeleor geodezice

12.3 Etapele parcurse la realizarea rețelei geodezice de îndesire.

12.4 Metode de îndesire a rețelei geodezice

12.1 Poziționarea rețelelor geodezice

Reţeaua geodezică trebuie să asigure densitatea punctelor necesare în zona de lucru şi în zona limitrofă, pentru executarea lucrarilor. In configuraţia reţelei vor fi cel puţin 4 puncte din reţeaua geodezica de sprijin, astfel încât, poligonul format să includă punctele reţelei de îndesire.

Reţeaua geodezică de îndesire şi de ridicare se realizează prin triangulaţie, trilateraţie, reţele de drumuiri poligonometrice sau prin înregistrari satelitare (Russu A., 1982).

Reţelele geodezice de îndesire sunt compensate ca reţele libere. Abaterea standard medie de determinare a punctelor nu trebuie să fie mai mare de ± 5 cm în poziţie planimetrică şi se calculează cu relaţia:



unde: n = numărul de puncte din reţea; Q_XX, Q_YY – elementele de pe diagonala principală a matricei coeficienţilor de pondere ai necunoscutelor şi S₀ – abaterea standard a unităţii de pondere.
12.2 Clasificarea rețeleor geodezice

12.3 Etapele parcurse la realizarea rețelei geodezice de îndesire.

12.4 Metode de îndesire a rețelei geodezice
14. Rețea geodezică de ridicare (4 ore)

14.1 Clasificare

14.2 Densitatea punctelor rețelei de ridicare

14.3 Materializarea pe teren a rețelei de ridicare

14.4 Metode de dezvoltare a rețelelor de ridicare

14.5 Compensarea rețelei de ridicare
14.1 Clasificare

Sunt create pentru asigurarea numărului de puncte necesare măsurătorilor topografice şi cadastrale de detaliu. Punctele reţelelor geodezice de ridicare sunt determinate prin intersecţii înainte, retrointersecţii, intersecţii combinate, drumuiri poligonometrice, cu utilizarea punctelor din reţeaua geodezică de sprijin şi de indesire.

Densitatea reţelelor geodezice de ridicare se stabileşte în raport cu suprafaţa pe care sunt executate lucrările. Abaterea standard de determinare a unui punct nu trebuie sa depaseasca: în intravilan ± 10 cm şi in extravilan ± 20 cm, în zonele de şes, ±30 cm, în zonele colinare, ±50 cm, în zonele de munte. Abaterile sunt calculate cu relaţiile:





14.2 Densitatea punctelor rețelei de ridicare

14.3 Materializarea pe teren a rețelei de ridicare

14.4 Metode de dezvoltare a rețelelor de ridicare

14.5 Compensarea rețelei de ridicare