Пояснительная записка. 1 ПЗ по Архитектуре полная. 1. Архитектура

• Название: 1. Архитектура
• Анкор: Пояснительная записка
• Дата: 14.06.2022
• Размер: 377.56 Kb.
• Имя файла: 1 ПЗ по Архитектуре полная.docx
• Тип: Документы; #591485
• страница: 9 из 16

4.3.12 Технико-экономические показатели

Таблица 4.3.7

№	Показатели	Единица измерения	Всего
1	Сметная стоимость СМР по строительству жилого дома	тыс. руб.	40687,3
2	Общая трудоемкость СМР по строительству жилого дома	чел.*дни	8271
3	Стоимость временных зданий и сооружений	тыс. руб.	1005,136
4	Удельные затраты на временные здания и сооружения	%	2,1
5	Нормативная продолжительность строительства	мес.	12
6	Планируемая продолжительность строительства	мес.	11,68

7. Научно-исследовательская часть

Критерии деформирования и разрушения железобетонных элементов.

Развитие современных вычислительных программ по расчету и моделированию напряженно-деформиро­ванного состояния как отдельных конструкций, так и зданий и сооружений в целом из железобетона немыс­лимо без использования общих моделей деформиро­вания и разрушения бетонных и железобетонных эле­ментов при различных напряженных состояниях, хотя модели начали разрабатываться задолго до развития компьютерных методов. Фактически, общие критерии и модели - это основной раздел компьютерных мето­дов, в которых учитываются реальные физико-механи­ческие и реологические свойства строительных мате­риалов (в данном случае бетона и железобетона), и их влияние на характер работы конструкций под на­грузкой.

Однако в вопросах построения современных (в последние 10-15 лет) отечественных промышленных вычислительных программ для расчета железобетон­ных конструкций наблюдаются серьезные негативные Тенденции. Речь идет о полном или частичном игнори­ровании факторов нелинейности и трещинообразования бетона и железобетона на уровне закладываемых связей между напряжениями и деформациями {физи­ческих соотношений), что приводит к искажению ре­альной картины деформирования конструкций, а в ито­ге - к понижению надежности конструктивных решений в одних случаях и неоправданному перерасходу ма­териалов в других.

Причина "засилья" линейных методов в основном кроется в ограниченных финансовых возможностях разработчиков {программы линейных расчетов намно­го проще нелинейных). Сточки зрения готовности не­линейных моделей к внедрению их в программы и про­граммные комплексы, особых препятствий нет. Пожа­луй, можно указать лишь на программный комплекс Лира-Windows, разработчики которого наметили и ин­тенсивно осуществляют программу по учету физичес­кой нелинейности при расчете пластин и оболочек.

Коротко остановимся на разработках НИИЖБ по этой проблеме (традиционно в последние 20 лет общие модели деформирования бетона и железобетона и кри­терии оценки прочности разрабатывались в лаборато­рии механики железобетона НИИЖБ). В основном об­ратим внимание на физические предпосылки, опреде­ляющие качество моделей. К общим моделям и крите­риям относим таковые для бетонных и железобетон­ных элементов в общем случае объемного напряжен­ного состояния {естественно, из них следуют и все ча­стные случаи напряженных состояний).

Критерии прочности бетонов

Начало исследованиям общих критериев прочнос­ти в НИИЖБ {точнее, в бывшем ЦНИПС) было положе­но работами А.А. Гвоздева которые нашли обобщение в [2]. Основные выводы этих исследований сводились к следующему;

- напряженное состояние оказывает значительное влияние на прочность элементов;

- классические теории прочности, включая теорию Мора, к бетону (без значительных модификаций) не применимы;

- следует учитывать влияние среднего напряже­ния σ₂ на прочность, а также влияние эффекта дилатации;

- преобладающим является отрывной механизм разрушения.

Законченного критерия прочности А.А. Гвоздевым не было предложено, однако указанные выводы несом­ненно повлияли на процесс построения общих критеиев прочности в нашей стране. Физическая сторона проблемы в дальнейшем получила развитие в работах О.Я. Берга.

К важной вехе развития критериев прочности мож­но отнести разработку экспериментального оборудова­ния, экспериментальных методик и проведение в тече­ние - 20 лет (1970 -1990 гг.) значительных эксперимен­тальных исследований в НИИЖБ над бетонными эле­ментами при различных объемных и плоских напряжен­ных состояниях. Работы проводились А.В. Яшиным и его многими аспирантами под руководством А.А. Гвоз­дева. Среди других значимых экспериментальных центров того времени следует выделить центр под ру­ководством О.Я. Берга, позже Е.Н. Щербакова (ЦНИИС Минтрансстроя) и центр Ю.Н. Малашнина -И.М. Безгодова (МИСИ). Результаты этих эксперимен­тальных исследований (к сожалению, в настоящее вре­мя полностью прекратившиеся) позволили значитель­но уточнить теоретические построения критериев проч­ности и приблизить их к адекватному описанию экспе­риментальных данных. Среди теоретических построе­ний сотрудников НИИЖБ следует выделить построе­ния А.В. Яшина, Е.С. Лейтеса, хотя их применимость ограничивается плотными бетонами. Более общий критерий прочности, относящийся к различным бето­нам (плотным и пористым), разработан Н.И. Карпенко (рис. 7.1). Среди работ сотрудников других институтов по построению критериев прочности можно указать на пионерные работы ГА. Гениева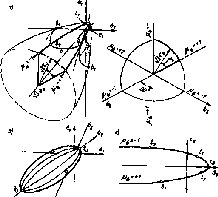





Рис.7.1. Схемы современных поверхностей прочности

а, в, г — для плотных бетонов; б — для пористых бетонов

и В.Н. Киссюка (ЦНИИСК), работы Л.К. Лукши (ПИ, Минск), В.М. Круглова (МИИТ), М.Б. Лившица (НИИЖТ), Т.А- Балана (ПИ, Кишинев), А.Б. Пирадова (ПИ, Тбилиси) и др.

Большинство современных предложений сводятся к построению феноменологических критериев в виде функциональных зависимостей между первым (I₁) инвариантом тензора напряжений, вторым (D₂) и третьим (D₃) инвариантом девиатора напряжений и характерис­тиками (константами) материала rj в виде

F(I₁, D₂, D₃, R_i) = 0(7.1)

или в виде связей между октаэдрическими нормаль­ными (σ₀) и касательными (₀) напряжениями и пара­метром Лоде-Надаи (_σ)

(₀, σ₀,_σ ,R_i)=0 (7.2)

К наилучшему согласованию с данными экспериментов приводят критерии типа (7.2).

Условия прочности железобетона

Различают условия прочности элементов с трещи­нами и без трещин. Проверка прочности элементов без трещин сводится к проверке прочности бетона (по ука­занным выше критериям) и проверке прочности арма­туры как для двухкомпонентного материала. Прочность элементов с трещинами также оценивается по двум критериям. Один из них оценивает прочность армату­ры в трещинах разрушения на растяжение, а второй -прочность блоков (или полос в плоском случае) бетона между трещинами на сжатие. Впервые такая двойствен­ная система критериев была введена в ряде работ ав­тора статьи и обобщена в монографии.

Развитие условий прочности железобетонных эле­ментов с трещинами по арматуре (или условий текуче­сти арматуры с физической площадкой текучести) бе­рет свое начало от работ К. Иогансена и А.А. Гвоздева по расчету плит. К. Иогансен записал условие прочно­сти по наклонной трещине разрушения (условно - из­лому плиты) в виде:


M_n = M_txsin ²α + M_tycos²α. (7.3)

где M_n - изгибающий момент по линии излома, M_tx. M_ty -предельные моменты, воспринимаемые растянутой армату­рой одного (х) и второго (у) направлений относительно верх­ней сжатой зоны. Неизвестной величиной в условии (7.3) явля­ется угол а наклона трещины разрушения (пластического шар­нира для арматуры с физической площадкой текучести), что создает определенную неопределенность при использовании этого критерия. Этого недостатка лишено более общее условие текучести арматуры А.А. Гвоздева:

(M_tx - M_x)(M_ty - M_y) - M²_xy =0 (7.4)

Условие (7.4) относится лишь к изгибаемым плитам, кроме этого в нем не учитывается влияние нагельного эффекта в арматуре в трещинах, что может сказывать­ся на точности расчета, особенно для арматуры без физической площадки текучести. В работах Н.И. Кар­пенко предложен путь устранения этих недостатков и получены условия прочности для различных конструкций:

- плит и оболочек при совместном действии мо­ментов (М_x, M_y. M_xy) и нормальных сил (N_x, N_y, N_xy) в виде

(M_tx_x¹-M_x-N_xZ_b)(M_ty_y¹-M_y- N_y Z _b) - (M_xy + N_xy Z _b)² 0 (7.5)

где Z _b - расстояние от срединной поверхности до центра тяже­сти эпюры в бетоне сжатой зоны;
- конструкций типа балок-стенок

(σ _sx- σ _x)(σ _sy- σ _y)-  _xy² 0 (7.6)

- объемных конструкций в виде равенства нулю
определителя [7.6, 7.7]

(σ _sx- σ _x)  _xy  _xz

 _yx (σ _sy- σ _y)  _yz 0 (7.7)

 _zx  _zy (σ _sz- σ _z)

где

σ _sx=R_sx_sx_x¹, σ _sy=R_syμ_sy_y ¹ , σ _sz= _szμ_sz_z ¹ ,

здесь _sx, μ_sy, μ_sz- коэффициенты армирования по ортогональным направлениям; _х, _у, ₂-функции, учитывающие влияние касательных напряжений в ар­матуре; R_sx, R_sy, R_sz - расчетные сопротивления арма­туры (для арматуры без площадки текучести это неко­торые переменные величины). Расчетные схемы для вывода критериев приведены ниже.

В случае выполнения классических предпосылок _х=_у=₂=1. При этом условия (7,5) - (7,7) значитель­но упрощаются и их удобно использовать для опреде­ления несущей способности конструкций статическим методом теории предельного равновесия. В нашей стране больше известен кинематический метод, кото­рый согласно теоремам А.А. Гвоздева дает верхнюю оценку несущей способности, в то время как статичес­кий метод приводит к нижней (наиболее безопасной) оценке.

Указанные критерии дополняются критериями по оценке прочности сжатых полос бетона между трещи­нами. Они имеют вид (7.5) - (7.7), однако величины σ_si(i = х, у, z) заменяются на величины R_p - прочности полос на сжатие и изменяются знаки внутри круглых скобок перед нормальными напряжениями, а также в (7.7) перед касательными компонентами. Отдельно ста­вятся критерии прочности плит по сжатой зоне. Таким образом получается замкнутая система критериев проч­ности для элементов с трещинами.

Заметим, что критерии (7.4) - (7.7) используются не только для оценки прочности армированных конструк­ций, но и для подбора необходимого по прочности ар­мирования. Для последних целей можно использовать исходные системы уравнений, из кото­рых следуют критерии (7.4) - (7.7). Анализируя зависимос­ти (7.4) - (7.7), можно видеть, что необходимое по прочно­сти армирование зависит не только от нормальных ком­понент усилий и напряжений, но и в значительной сте­пени от касательных компонент. Этот фактор зачастую игнорируется разработчиками программ, что приводит к заметным ошибкам при проектировании.

Нельзя не указать и на применение критериев проч­ности в расчетах конструкций методом предельного равновесия .

Применение кинематического метода предельного равновесия к расчету железобетонных конструкций рассматривалось в работах А.А. Гвоздева, А. Р. Ржаницина, С.М. Крылова, Л.Н. Зайцева, Г.К. Хайдукова, В.В. Шугаева, Ю.В. Чиненкова и многих других. Статический метод применялся в работах М.И. Рейтмана, Н.И. Карпенко, A.M. Проценко, Б.Ю. Мирзабекяна.

Общие модели деформирования бетона

Бетон - физический нелинейный материал, причем его физическая нелинейность при многоосном напря­женном состоянии проявляется на всех стадиях дефор­мирования, увеличиваясь по мере приближения к вы­ходу на предельную поверхность разрушения. Перво­начальные попытки учесть нелинейность бетона дела­лись на базе классических теорий пластичности - ма­лых упругопластических деформаций А.А. Ильюшина и теории Прандтля — Рейса. Известно, что в этих тео­риях используются гипотезы об изотропии материала в процессе деформирования и об упругом изменении объема, пластические деформации развиваются толь­ко за счет изменений формы, обусловленной девиа-торными компонентами. Однако эти предпосылки не подтверждаются данными экспериментов. Так уже в ранней работе А.А. Гвоздева отмечается, что при невысоких уровнях напряжений объем бетона нелиней­но уменьшается, а при напряжениях, близких к пре­дельным, увеличивается также по нелинейному зако­ну. Экспериментальное подтверждение этого эффекта дал А.В.Яшин]. Это явление получило название эффекта дилатации (разуплотнения, дилактации) и А.А. Гвоздев объяснил его появлением трещин отры­ва. Н.И. Карпенко показал, что процесс появления и развития трещин отрыва носит направленный характер, что приводит к анизотропии материала. К настоящему времени можно выделить три направления в построе­нии нелинейных связей между напряжениями и дефор­мациями, в которых в той или иной форме учитывают­ся указанные выше нелинейные свойства бетона:

1. 
   На основе модифицированных предпосылок тео­рии малых упругопластических деформаций;
   
2. 
   На основе модели бетона как нелинейно дефор­мируемого материала с приобретаемой ортотропией;
   
3. 
   На основе модификации предпосылок теории те­чения.
   

В первом подходе гипотеза об изотропии материа­ла сохраняется и эффект дилатации учитывается в сред­нем по объему (в виде образования равномерно рас­сеянных по объему трещин отрыва). Это направление заложено работами ГА. Гениева, в которых модуль ма­териала является функцией его напряженного состоя­ния и дополнительно вводится новая характеристика -модуль дилатации. В НИИЖБ эта теория существенно развита в работах А.В. Яшина и E.G. Лейтеса, которые на основе обработки большого числа эксперименталь­ных данных получили аналитические функции для мо­дуля дилатации и, кроме того, учли возможность про­грессирующего разрушения бетона путем учета нис­падающей ветви диаграммы деформирования матери­ала .

Интересные предположения по развитию этого на­правления сделаны ЛИ. Козачевским, В.М. Кругловым и рядом других исследователей.

Приоритет развития второго направления принад­лежит исследователям НИИЖБ. Еще А.А.Гвоздев, рас­сматривая теорию А.А. Ильюшина, основанную на по­стулате изотропии, высказал предположение, что в материале в процессе деформирования может разви­ваться деформационная анизотропия. Законченная ортотропная модель бетона (видимо, впервые в нашей стране) была разработана Н.И. Карпенко. Физические соотношения в этой модели записываются как для ортотропного ма­териала с осями симметрии свойств, совпадающих с осями главных напряжений σ₁ ,σ₂, σ₃ или дефор­маций ε₁, ε₂, ε₃. Три модуля и три коэффициента по­перечной деформации

Рис.7. 2. Схемы армирования



этой модели являются функци­ями главных напряжений или деформаций и их комби­наций. Ортотропная модель позволяет учитывать на­правленное развитие эффекта дилатации и неоднород­ность деформирования при сжатии и растяжении, и этим в большей степени отражает реальный характер дефор­маций бетона при плоском и объемном напряженном состоянии. Среди работ других исследователей, вне­сших вклад в развитие ортотропной модели, следует указать на работы А.С. Городецкого, B.C. Здоренко (И-ИАС, г. Киев), Т.Д. Балана, С.Ф. Клованича, Г.Р. Вид­ного (ПИ, Кишинев), А.Н. Петрова (ПИ, Петрозаводск) и некоторых других (работы многих из этих исследова­телей начинались в лаборатории механики железобе­тона ГУП НИИЖБ).

Развитие теорий типа течения применительно к бе­тону также идет по пути учета нелинейности изменения объема и эффекта дилатации. При этом пластичность бетона уже нельзя ассоциировать с поверхностью те­кучести при помощи закона ортогональности и посту­лата Друкера. Неассоциированные формулировки раз­вивались в работах В.М. Круглова и его учеников.

Современные теории течения для бетона еще на­ходятся в стадии становления. В НИИЖБ это направ­ление получило нетрадиционное развитие в виде раз­работки некоторой ортотропной модели бетона в при­ращениях. Развитие этого направления перспек­тивно с позиции описания сложных режимов нагружения.

Анализируя в общем уровень развития моделей де­формирования бетона, можно отметить, что, пожалуй, две первые модели (ортотропная модель и модифици­рованная модель малых упруго-пластических дефор­маций) уже достигли такого уровня разработки, что могут использоваться в нелинейных расчетных программах.

Модели деформирования железобетона с трещинами

В разработке этих наиболее сложных моделей ис­следователям НИИЖБ принадлежит, пожалуй, главен­ствующая роль. Исторически первой моделью дефор­мирования железобетона является модель В.И. Мура-шева для изгибаемых элементов с трещинами, которая хорошо зарекомендовала себя при расчете балок, колонн, балочных плит. Однако, детальные экс­периментальные исследования, выполненные в 1961 г. в НИИЖБ А.Н. Королевым и С.М. Крыловым под руководством А.А. Гвоздева над квадратными оперты­ми по контуру плитами при равномерной нагрузке, по­казали, что опытные прогибы значительно отклоняются отданных расчета по теории В.И. Мурашева (при этом, учитывая одинаковое армирование по двум направле­ниям, цилиндрическая жесткость заменялась на балоч­ную жесткость по В.И. Мурашеву). Авторы предложили эмпирический путь определения прогибов, однако эти исследования дали значительный импульс к поис­ку новых построений. Были предложены несколько моделей деформирования железобетона с трещинами при неодноосном напряженном состоянии: анизотроп­ная (работы Н.И. Карпенко по теории плит и стен с тре­щинами, начальные исследования выполнялись под руководством А.А. Гвоздева и С.М. Крылова); трансверсальноизотропная (работы ГА. Гениева и ГА. Тюпи-на); ортотропная (работы Я.Д. Лившица, М.М. Онищен-ко, В.Н. Байкова, Е.А. Палатникова по плитам, И.Е. Ми-лейковского по оболочкам и др.), где в основном кор­ректировалась жесткость на кручение вплоть до равен­ства нулю (оси ортотропии совмещались с направле­ниями арматуры), а изгибаемые жесткости определя­лись по В.И. Мурашеву. Однако ортотропные модели не объясняли факт эффект значительного удлинения труб и их расшире­ния по радиусу при частом кручении после образова­ния трещин (опыты Э.Г. Елагина, выполненные в НИ­ИЖБ под руководством Н.Н. Лессич), в то время как анизотропная модель позволила с хорошей точностью определить как углы закручивания, так и удлинение и расширение труб. В дальнейшем автором статьи был разработан общий случай анизотропной модели для объемного напряженного состояния. Влияние температур­ных деформаций учтено в работах Н.И. Карпенко и С.Ф. Клованича. Армирование характеризуется коэф­фициентами армирования μ_Siпо направлениям, диа­метром стержней d_Sj и направляющими косинусами U к выбранным осям i = х, у, z (рис. 7.2а,б). Выделяются два состояния работы элементов: без трещин и с тре­щинами. Для элементов без трещин общая матрица связи напряжений с деформациями [D] формируется в два этапа. Сначала в матрице бетона учитываются два побочных фактора - влияние арматуры на сдвиг и на деформации в поперечном направлении по объемным коэффициентам содержания, а затем учитывается ос­новной фактор - совместность осевых деформаций ар­матуры и бетона.

Напряжения в элементе являются составными, со­стоящими из напряжений в бетоне и приведенных на­пряжений в арматуре. В результате связь между на­пряжениями {σ} и деформациями {ε}принимает вид (при наличии начальных напряжений {σ₀}:

{σ} = [D] {ε}+{σ₀} (7.8)

Полагается, что когда главные растягивающие на­пряжения в бетоне достигают предельных значений, найденных по условиям прочности, в нем образуются трещины. Вывод физических соотношений, устанавли­вающих связи между напряжениями и деформациями в железобетонном элементе с трещинами, является

наиболее важным в цепочке теоретических построений. При этом учитываются следующие факторы:

- углы наклона трещин к арматуре и схемы их пе­ресечения трещин (различаюттри схемы трещин, при­веденные на рис. 7.3);

- раскрытие трещин а_сг и сдвиг их берегов  (рис.7. 4);

- жесткость арматуры при осевых деформациях (рис. 7.4,б) под действием напряжений в арматуре в зоне трещины с учетом влияния на деформации сил сцеп­ления арматуры с полосами и блоками бетона между трещинами (рис. 7.4,в);

- жесткость арматуры при тангенциальных пере­мещениях ее относительно берегов трещин под дей­ствием касательных напряжений в арматуре в зоне тре­щины с учетом




2 трещина 3 трещин
Рис.7.3. схемы трещин

податливости бетонного основания у берегов трещины (рис. 7.4,г);

- жесткость остаточных бетонных связей зацепле­ния берегов трещин при их сдвигах (обычно учитыва­ются в случае малой ширины раскрытия трещин);

- нарушение совместности осевых деформаций арматуры и бетона между трещинами при сохранении условий совместности перемещений арматуры и бето­на в центре полос или блоков бетона между трещина­ми (в точке А рис. 7.3,в).

Напряжения в арматуре а трещинах определяются двояким способом - через средние деформации эле­мента (по схемам рис. 7.3 - рис. 7.8) или непосредственно через нормальные и касательные напряжения в эле­менте (по схемам рис. 7.9 - рис. 7.10). При этом трещины в общем случае располагаются наклонно к на­правлениям арматуры. Естественно, напряжения, пред­ставленные на рис. 7.9а и рис. 7.9б, в действительности совмещены на гранях одного тетраэдра (они разделя­ются лишь для удобства выкладок). Указанные схемы служат также для вывода критериев прочности (7.6)-(7.7)

Указанные выше предпосылки не укладывались в традиционные пути построения физических соотноше­ний, используемых в композитных материалах, и тре­бовали новых подходов. Фактически необходимо было в малом элементе среды (условно в точке) иметь од­новременно два вида напряжений в каждом компонен­те (большие напряжения в арматуре в трещинах и прак­тически равные нулю напряжения в бетоне, и одновре­менно значительно меньшие напряжения в арматуре на площадках, нормальных к трещинам, и, наоборот, большие по модулю напряжения в бетоне на этих пло­щадках). В работах автора статьи эта проблема была решена на пути использования несимметричных тен­зоров напряжений для компонент арматуры и бетона (вводятся 9 компонент вместо 6 без соблюдения усло­вия парности касательных величин). Лишь в сумме сим­метричные компоненты становятся симметричными (с соблюдением парности касательных напряжений).

Физические зависимости сначала устанавливают­ся в локальных координатах n, m, I, нормальных к тре­щинам, а затем переводятся в глобальную систему х. у, z. Как и прежде, каждое направление армирования задается коэффициентом армирования μ_siи таблицей направляющих косинусов относительно локальной си­стемы n, m, I (рис. 7.5,а). Количество арматуры, пересе­кающей грани единичного куба, показано на рис. 7.5,7.6. Напряжения по граням такого элемента (рис. 7.6) фор­мируются по-разному. На площадках-трещинах дей­ствуют нормальные и касательные напряжения в арматуре в зоне трещины, а на других площадках учиты­ваются только средние напряжения σ_st. Общие на­пряжения (рис. 7.7,а) получаются суммированием напря­жений в бетоне (рис. 7.7,7.6) и в арматуре (рис. 7.7,в).

Про­ецируя усилия, приложенные к граням элемента (см. рис. 7.6), на оси n, m, I, получим составляющие общих напряжений. Например, нормальные относительных деформаций бетона между трещинами (ε_br,* _bkr,* _brk).

Рис.7.4. Деформирование арматуры в элементах с трещи­нами.

Деформации от раскрытия трещин и возможного сдвига их берегов определяются по схе­мам, показанным на рис. 7.8. Эти деформации составля­ют девятикомпонентный вектор-столбец, они также об­разуют несимметричный тензор второго ранга: