1 Астрономические системы координат
 Скачать 2.84 Mb. Скачать 2.84 Mb.
|
|
1.3.4. Среднее солнечное время. Всемирное время. Чтобы устранить неудобства исчисления времени по истинному Солнцу и все же иметь возможность измерять время по движению Солнца, принято вести его счет по движению некоторой воображаемой точки, движущейся равномерно по экватору и называемой средним экваториальным Солнцем. Оно всегда находится недалеко от круга склонения центра истинного Солнца. Связь между этой точкой и центром Солнца устанавливается через так называемое среднее эклиптическое Солнце. Представим себе фиктивную точку, которая равномерно движется по эклиптике со скоростью, равной средней скорости движения истинного Солнца, соответствующей средней скорости движения Земли. Эта фиктивная точка называется средним эклиптическим Солнцем. Среднее эклиптическое солнце - воображаемая точка, движущаяся равномерно в плоскости эклиптики по кругу, построенному на линии апсид, как на диаметре. Линией апсид называется прямая, соединяющая перигей и апогей. Среднее эклиптическое солнце проходит одновременно с центром Солнца точку перигея, ближайшую к Земле, и апогея, самую отдаленную точку от Земли. Понятно, что воображаемая точка в своем движении по эклиптике то обгоняет истинное Солнце, то отстает от него. В самом деле, так как скорость движения Солнца близ перигея больше постоянной скорости движения среднего эклиптического солнца, то после одновременного прохождения через перигей истинное Солнце обгоняет среднее эклиптическое - оно идет впереди. Но так как скорость истинного Солнца по закону Кеплера постепенно замедляется, то среднее эклиптическое Солнце начинает его догонять и настигнет его в точке апогея. После одновременного прохождения через апогей, наоборот, истинное Солнце отстает от среднего эклиптического и т. д. Для некоторого интервала времени долгота среднего эклиптического Солнца равняется средней долготе истинного Солнца, т.е. 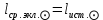 (56) (56)Однако введение среднего эклиптического Солнца ещё не приводит нас к постоянной единице времени, так как снимает только один из факторов, вызывающих изменяемость единиц времени, измеряемых в истинных солнечных единицах, а именно: неравномерность видимого движения Солнца по эклиптике. Второй фактор, наклон экватора к эклиптике, вызывает неравномерное возрастание прямого восхождения среднего эклиптического Солнца и, следовательно, неравномерное изменение его часового угла. 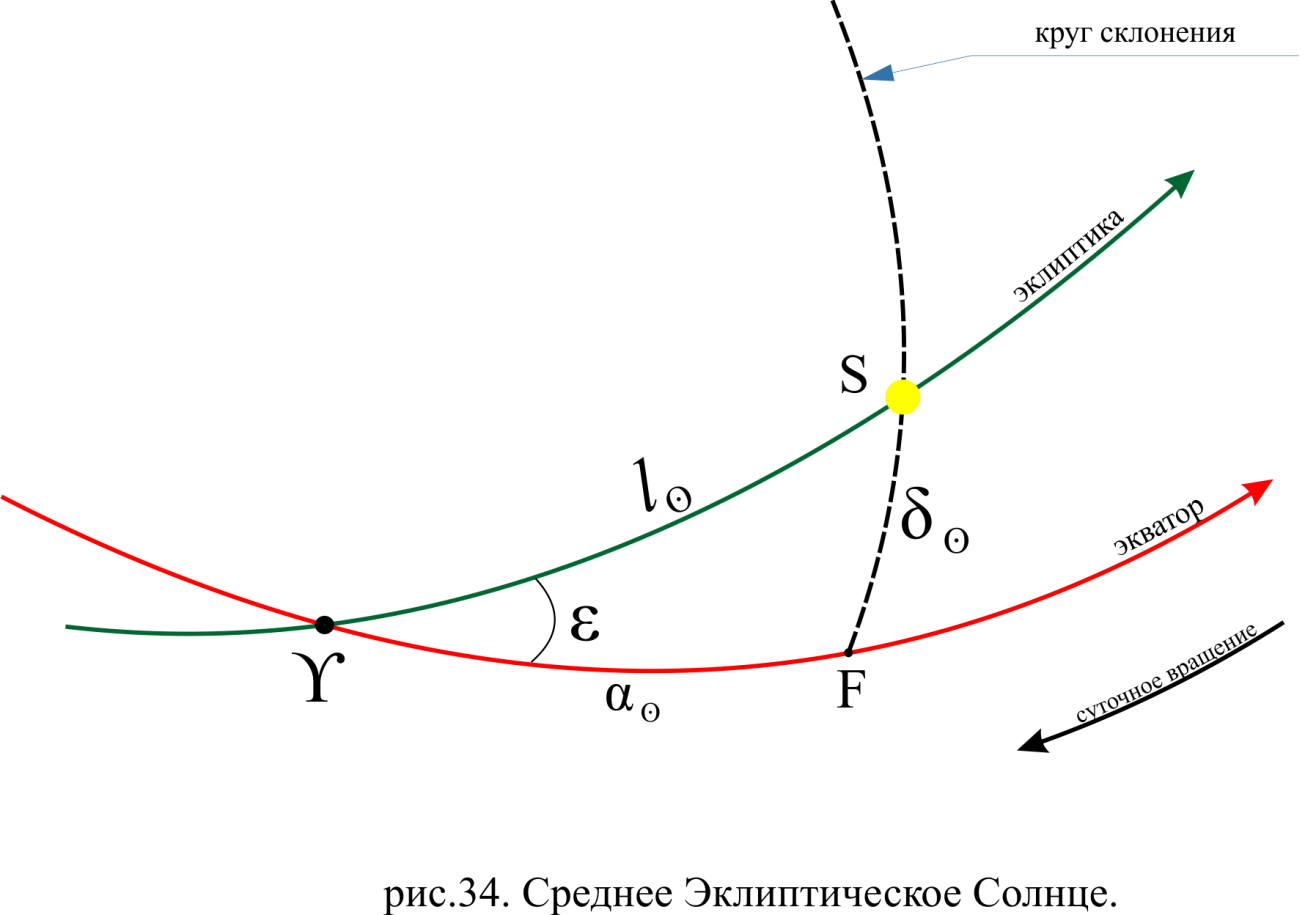 В самом деле, из прямоугольного сферического треугольника 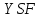 (рис. 34), образованного при пересечении дуг экватора (рис. 34), образованного при пересечении дуг экватора 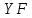 , эклиптики , эклиптики 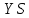 и круга склонения и круга склонения 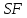 среднего эклиптического Солнца, по правилу Непера-Модюи находим: среднего эклиптического Солнца, по правилу Непера-Модюи находим: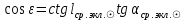 , (57) , (57)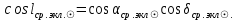 , (58) , (58)где 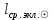 , , 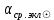 и и 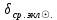 - соответственно долгота, прямое восхождение и склонение среднего эклиптического Солнца. - соответственно долгота, прямое восхождение и склонение среднего эклиптического Солнца.Из выражение (57) имеем: 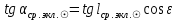 (59) (59)Дифференцируя (59) по переменным 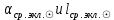 , считая , считая 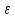 постоянной величиной, равной постоянной величиной, равной 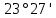 , получим , получим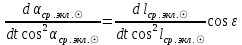 (60) (60)Подставляя в (60) выражение 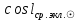 из (58), имеем: из (58), имеем: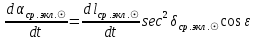 (61) (61)Так как среднее эклиптическое Солнце движется по эклиптике равномерно, со скоростью, равной средней скорости движения истинного Солнца, то производная 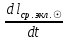 величина постоянная. величина постоянная.В правую часть формулы (61) входит 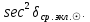 Так как склонение среднего эклиптического Солнца - величина переменная, то и скорость изменения его прямого восхождения, т. е. производная Так как склонение среднего эклиптического Солнца - величина переменная, то и скорость изменения его прямого восхождения, т. е. производная 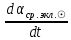 величина переменная. величина переменная.Таким образом, часовой угол среднего эклиптического Солнца, а следовательно и время, им определяемое, будут возрастать неравномерно. Для того чтобы исключить влияние фактора 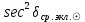 представим себе точку, которая равномерно движется по экватору в ту же сторону, что и Истинное Солнце. Эта фиктивная точка называется средним экваториальным Солнцем. представим себе точку, которая равномерно движется по экватору в ту же сторону, что и Истинное Солнце. Эта фиктивная точка называется средним экваториальным Солнцем. Среднее экваториальное Солнце связано со средним эклиптическим определенными условиями: двигаясь по экватору с той же скоростью, с которой среднее эклиптическое Солнце двигается по эклиптике, оно одновременно с ним проходит через точки весеннего и осеннего равноденствия. Следовательно, прямое восхождение среднего экваториального Солнца всегда равно долготе среднего эклиптического Солнца или средней долготе истинного Солнца, т. е. 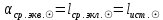 (62) (62)Из наблюдений Солнца и планет по законам небесной механики можно вычислить среднее увеличение долготы Солнца 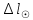 за единицу времени. Кроме этого можно определить долготу среднего эклиптического Солнца для какого-либо момента времени за единицу времени. Кроме этого можно определить долготу среднего эклиптического Солнца для какого-либо момента времени 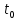 . Далее, зная . Далее, зная 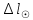 и и 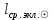 для момента для момента 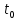 , можно найти долготу среднего эклиптического Солнца для любого другого момента времени , можно найти долготу среднего эклиптического Солнца для любого другого момента времени 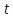 . . Таким образом, для любого момента времени взаимное расположение истинного Солнца и среднего экваториального Солнца может быть определено. Так как среднее экваториальное Солнце движется по экватору, и притом равномерно, часовые углы его, при условии, что влияние неравномерностей во вращательном движении Земли во внимание не принимается, возрастают тоже равномерно и, следовательно, оно вполне пригодно для измерения времени. До 1925 г. за начало средних солнечных суток принимался момент верхней кульминации среднего экваториального Солнца, т. е. средний полдень. С 1 января 1925 г. по указанным выше причинам за начало средних солнечных суток принимается момент нижней кульминации среднего экваториального Солнца, т. е. средняя полночь. Промежуток времени между двумя последовательными нижними кульминациями среднего экваториального Солнца на меридиане данного пункта называется средними солнечными сутками. Средние солнечные сутки подразделяются на 24 средних часа, средний час содержит 60 средних минут, средняя минута 60 средних секунд. В момент нижней кульминации среднего экваториального Солнца, т. е. в среднюю полночь, среднее солнечное время равно 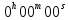 , а часовой угол среднего экваториального Солнца , а часовой угол среднего экваториального Солнца 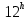 . .Время, прошедшее от начала средних солнечных суток до любого другого момента, выраженное в средних солнечных часах, минутах и секундах, называется средним солнечным временем и обозначается буквой 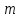 . .Среднее солнечное время численно равно часовому углу среднего экваториального Солнца ( 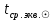 ) на данном меридиане, выраженному в часовой мере и увеличенному на ) на данном меридиане, выраженному в часовой мере и увеличенному на 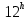 , т. е. , т. е.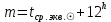 . (63) . (63)Среднее солнечное время Гринвичского меридиана называется всемирным, или мировым временем и обозначается UT (Universal Time) (в АЕ обозначается буквой M). С 1925 г. до 1960 г. оно являлось основным аргументом АЕ. Если часовой угол среднего экваториального Солнца на меридиане Гринвича обозначить через 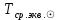 , то , то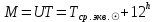 . (64) . (64)До 1960 г. средние солнечные сутки использовались для определения секунды. Секунда определялась как 1/86400 часть средних солнечных суток. Это означает, что длительность секунды зависела от скорости вращения Земли. После появления кварцевых, а затем атомных часов, неравномерность вращения Земли была обнаружена. Это привело к отказу от средних солнечных суток как меры хранения времени и замене определения секунды. Сейчас всемирное время рассматривается как мера вращения Земли. Ясно, что при равномерном движении среднего Солнца по экватору оно будет ежедневно отставать от точки 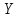 на постоянную величину и, следовательно, средние сутки будут длиннее звёздных на 3m56,56s Продолжительность средних суток постоянна и равна средней за год продолжительности истинных суток. на постоянную величину и, следовательно, средние сутки будут длиннее звёздных на 3m56,56s Продолжительность средних суток постоянна и равна средней за год продолжительности истинных суток. Поскольку измерение среднего времени связано с часовым углом среднего Солнца, а следовательно, и с меридианом наблюдателя, то на каждом географическом меридиане будет свое местное среднее время. Местное среднее время m – промежуток времени в средних единицах от момента нижней кульминации среднего Солнца на местном меридиане до данного физического момента. В любой точке заданного географического меридиана в один и тот же физический момент местное среднее время одинаково. Это шкала измерения времени, в основу которой положено вращение Земли вокруг оси относительно среднего Солнца. Местное среднее время m какого- либо пункта с долготой 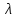 связано с всемирным временем UT (M) соотношением связано с всемирным временем UT (M) соотношением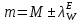 (65) (65)Ввиду того, что календарный счёт суток ведется именно по среднему времени, необходимо как местному, так и Гринвичскому (всемирному) времени приписывать дату. На звёздное время это требование не распространяется, так как звёздное время своего календарного счета не имеет и к звёздному времени можно прибавлять или вычитать 24 ч, не нарушая правильности решения задачи. 1.3.6. Время на разных меридианах. Местное и Гринвичское время. Звёздное время 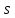 , истинное солнечное время , истинное солнечное время 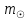 и среднее солнечное время m в какой-либо точке земной поверхности называются соответственно местным звёздным, местным истинным солнечным и местным средним солнечным временем этой точки. и среднее солнечное время m в какой-либо точке земной поверхности называются соответственно местным звёздным, местным истинным солнечным и местным средним солнечным временем этой точки. В каждой точке земной поверхности считается свое местное время. В точках, расположенных на одном географическом меридиане, одноименное местное время (звёздное, истинное солнечное, среднее солнечное), определенное в один и тот же физический момент, одинаково. Рассмотрим, чему равна разность одноименных местных времен, определенных в один и тот же физический момент в двух пунктах А и В земной поверхности, расположенных на разных географических меридианах. Предположим, что 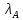 и и 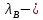 географические долготы пунктов А к В, причем оба пункта находятся к востоку от гринвичского меридиана. географические долготы пунктов А к В, причем оба пункта находятся к востоку от гринвичского меридиана.Для определения интересующей нас разности местных времен, воспользуемся II Астрономической теоремой, устанавливающей связь между разностью долгот пунктов земной поверхности и разностью часовых углов светила, наблюденных в этих пунктах в один и тот же физический момент времени: 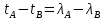 Применяя эту формулу к часовым углам точек, используемых для измерения времени, (т. е. к точке весеннего равноденствия, к истинному Солнцу, к среднему экваториальному Солнцу), относительно которых отсчитываются обороты Земли вокруг оси и часовые углы которых являются мерой времени, получим: 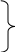 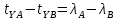 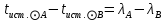 (68) (68)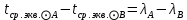 Принимая во внимание, что 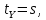 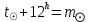 и и 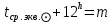 и подставляя эти равенства в выражения (68), получим следующие формулы: 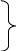 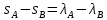 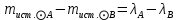 (69) (69)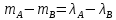 Следовательно, разность одноименных местных времен (звёздных, истинных солнечных или средних солнечных), определенных в один и тот же физический момент в двух разных пунктах земной поверхности, расположенных на разных меридианах, численно равна разности географических долгот этих пунктов, выраженных в часовой мере. Полученные нами формулы (69) играют важную роль в геодезической астрономии, особенно при долготных определениях. Из всех земных меридианов особое место в астрономии занимает Гринвичский меридиан, принятый за начальный при счете географических долгот. Поэтому в отличие от других меридианов местное время Гринвичского меридиана обозначается большими буквами, а именно:  - гринвичское звёздное время; - гринвичское звёздное время; - Гринвичское истинное солнечное время; - Гринвичское истинное солнечное время; - Гринвичское среднее солнечное время. - Гринвичское среднее солнечное время.Так как видимое суточное вращение небесной сферы происходит по часовой стрелке, с востока на запад, то, если пункт земной поверхности расположен к востоку от Гринвича, его местное время (звёздное, истинное солнечное, среднее солнечное) больше Гринвичского, причем разность между местным и гринвичским временем тем больше, чем дальше к востоку расположен пункт. И наоборот, если пункт расположен к западу от Гринвича, то его местное время меньше Гринвичского, причем разность между ними тем больше, чем дальше к западу расположен пункт. Предположим, что точка В - Гринвич (  ), а точка А - пункт земной поверхности, расположенный на любом другом меридиане, кроме Гринвичского. Тогда формулы (69) примут вид: ), а точка А - пункт земной поверхности, расположенный на любом другом меридиане, кроме Гринвичского. Тогда формулы (69) примут вид: 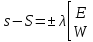 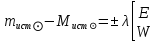 (70) (70)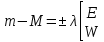 В этих формулах знак плюс соответствует долготам пунктов, расположенных к востоку от Гринвича, знак минус - к западу от Гринвича. Из формул (70) следует, что географическая долгота пункта от Гринвича (в часовой мере) равна разности местного и гринвичского времени. Формулы (70) имеют большое практическое значение, так как дают принципиальную основу для определения долгот пунктов от Гринвича. Формулы (70) могут быть также использованы для нахождения Гринвичского времени, если известны местное время и долгота пункта от Гринвича: 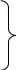 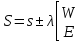 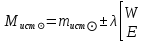 (71) (71)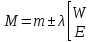 На основании изложенных выше соображений и формул (71) мы приходим к выводу, что для того чтобы привести в согласие стрелки своих часов с местным временем, человек, передвигающийся от Гринвича на восток, должен по мере своего передвижения переводить их вперед. Если бы он двигался от Гринвича на запад, то стрелки часов ему пришлось бы переводить назад. 1.3.7. Время поясное и декретное. Линия изменения даты. Из астрономических наблюдений мы получаем местное время того меридиана, на котором произведены наблюдения. Местное время может быть звёздным, истинным солнечным и средним солнечным. Для всех точек, лежащих на одном географическом меридиане, любое местное время в один и тот же момент одинаково. Однако, как бы близко ни лежали по долготе два каких-либо пункта на земной поверхности, в каждом из них в один и тот же физический момент будет разное местное время. Местное среднее время непрерывно изменяется с изменением географической долготы, увеличиваясь к востоку. И различие местных времен, и в частности среднего солнечного времени, на разных меридианах создает большие неудобства в практическом использовании среднего солнечного времени, особенно на телеграфе и транспорте. Так, в США, территория которых значительно простирается по долготе, к концу XIX в. на железных дорогах насчитывалось 75 разных систем исчисления времени. На узловых станциях там нередко выставляли трое часов: одни – для поездов, идущих на запад, другие – для поездов, идущих на восток, и третьи – для местного пользования. Необходим был способ счета времени, исключающий этот разнобой, причем способ общий для всей Земли. В 1879 г. канадский инженер-железнодорожник Сандфорд Флеминг разработал систему поясного времени. По этой системе поверхность Земли условно разделена меридианами на 24 часовых пояса так, чтобы разность граничных меридианов составляла 15° (в часовой мере – 1 ч). Наибольшую ширину часовые пояса имеют на экваторе Земли (около 1670 км), к северу и югу расстояние между ними постепенно уменьшается, доходя до нуля на географических полюсах. Во всех пунктах земной поверхности, расположенных в пределах данного часового пояса, в один и тот же физический момент считается одно и то же время: среднее солнечное время осевого меридиана этого пояса. Тогда разность между местным и поясным временем не будет превышать получаса. Счет центральных меридианов начинается с меридиана Гринвича, долгота которого равна 0h. Часовым поясам последовательно присвоены номера от 0 до 23, возрастающие с запада на восток. По проекту С. Флеминга границы часовых поясов должны проходить по географическим меридианам, но это требование соблюдается лишь в открытых морях и в необжитых районах. Строгое повсеместное соблюдение такого условия привело бы к тому, что на территории одного района или даже одного города было бы разное время. Поэтому в действительности границы часовых поясов проходят по горным хребтам, крупным рекам, сообразуясь с путями сообщений, природными и экономическими особенностями местности. При этом стараются по возможности объединить по времени районы, тяготеющие друг к другу в хозяйственном отношении. Так, например, Москва по долготе расположена во 2-м и 3-м часовых поясах, но целиком включена во 2-й часовой пояс. Если некоторый пункт расположен точно на граничном меридиане, то для него принимается поясное время часового пояса, лежащего к востоку от пункта. В 1884 г. Международная конференция в Вашингтоне приняла решение о введении поясного времени в ряде стран. В нашей стране поясное время введено с 1919 г. На территории РФ расположено 9 часовых поясов (со 2-го по 11-й). Ширина часового пояса в разных странах мира и даже в пределах территории одной страны может значительно отличаться от условно принятого распределения "поясного времени" на Земле. Например, в США и Канаде есть часовые пояса, превышающие по ширине условно принятые в 1,5‑2 раза, а на территории Китая, находящегося в пределах пяти условных часовых поясов, действует время одного из часовых поясов. Гринвичский меридиан является центральным меридианом нулевого пояса. Протяжение этого часового пояса – 7,5° к W и 7,5° к E от Гринвича. В 1-м часовом поясе центральным является меридиан с долготой 15°E. Поясное время этого часового пояса называется среднеевропейским временем. Центральный меридиан 2-го часового пояса имеет λ = 30°E. По такому же принципу разделены и все остальные часовые пояса. При пересечении границ часовых поясов поясное время меняется ровно на один час, минуты же и секунды на протяжении всех часовых поясов сохраняются одними и теми же, причем соответствуют минутам и секундам всемирного времени M (UTC). Таким образом система поясного счета времени устраняет неудобства, возникающие при использовании в повседневной жизни как местного, так и всемирного времени. |
