Алгоритм и структура данных. 1 Базовый процедурноориентированный алгоритмический язык

Название	1 Базовый процедурноориентированный алгоритмический язык
Анкор	Алгоритм и структура данных
Дата	03.11.2022
Размер	1.16 Mb.
Формат файла
Имя файла	Алгоритм и структура данных.docx
Тип	Документы #768957
страница	10 из 11

1 2 3 4 5 6 7 8 9 10 11

Операции

Линейное зондирование является компонентом схем открытой адресации^[en] для использования в хеш-таблицах для решения словарных задач. В словарной задаче структура данных должна работать с набором пар ключ-значение и должна обеспечивать возможность вставки и удаления пар, а также поиск значения, ассоциированного с ключом. В открытой адресации структурой данных служит массив T (хеш-таблица), ячейки которого T[i] (если не пусты) содержат единственную пару ключ-значение. Хеш-функция используется для отображения каждого ключа в ячейку таблицы T, куда этот ключ должен быть занесён, как правило, скремблируя ключи, так что ключи с близкими значениями не оказываются близко в таблице. Коллизия хеш-функции возникает, когда хеш-функция отображает ключ в ячейку, уже занятую другим ключом. Линейное зондирование является стратегией для разрешения коллизий путём размещения нового ключа в ближайшую следующую свободную ячейки^[3][4].

Поиск

Для поиска заданного ключа x проверяются ячейки таблицы T, начиная с ячейки с индексом h(x) (где h — хеш-функция), затем ячейки h(x) + 1, h(x) + 2, …, пока не будет найдена свободная ячейка или ячейка, в которой содержится ключ x. Если ячейка, содержащая ключ, найдена, процедура поиска возвращает значение из этой ячейки. В противном случае, если встретилась пустая ячейка, ключ не может находиться в таблице и процедура возвращает в качестве результата, что ключ не найден^[3][4]

Вставка

Для вставки пары ключ-значение (x,v) в таблицу (возможно, с заменой любой существующей пары с тем же ключом) алгоритм вставки проходит ту же последовательность ячеек, что и при поиске, пока не найдёт либо пустую ячейку, либо ячейку, содержащую ключ x. Новая пара ключ-значение размещается в этой ячейке^[3][4].

Если после вставки коэффициент загрузки таблицы (доля занятых ячеек) превышает некоторый порог, вся таблица может быть заменена на новую таблицу, размер которой увеличивается на постоянный множитель, как в случае динамического массива, с новой хеш-таблицей. Установка этого порога близким к нулю и использование высокого коэффициента расширения таблицы приводит к быстрым операциям, но требует больших затрат памяти. Обычно размер таблицы удваивается при достижении коэффициента загрузки 1/2, так что загрузка составляет от 1/4 до 1/2^[5]

Удаление

Когда удаляется пара ключ-значение, может оказаться необходимым перенести другую пару в эту ячейку, чтобы избежать получение пустой ячейки при поиске удалённого ключа

Можно удалить пару ключ-значение из словаря. Однако недостаточно просто очистить ячейку. Возможно, существует другая пара с тем же хеш-значением, которая была размещена где-то после занятой ячейки. После очистки ячейки поиск второго значения с тем же значением хеш-функции наткнётся на пустую ячейку, и пара не будет найдена.

Таким образом, при очистке ячейки i необходимо просмотреть последующие ячейки, пока не найдём пустую ячейку, либо ключ, который можно перенести в ячейку i (то есть ключ, хеш-значение которого равно или меньше i). Если найдена пустая ячейка, то можно очистить ячейку i и остановить процесс удаления. Если же найден ключ, который можно перенести в ячейку i, переносим его. Это приведёт к увеличению скорости поиска перенесённого ключа, а также очищает другую ячейку в блоке занятых ячеек. Необходимо продолжить поиск ключа, который может быть перенесён на это освободившееся место. Поиск ключа для переноса осуществляется до пустой ячейки, пока не достигнем ячейки, которая изначально была пуста. Таким образом, время выполнения всего процесса удаления пропорционально длине блока, содержащего удалённый ключ^[3].

Альтернативно, можно использовать стратегию ленивого удаления^[en], в которой пара ключ-значение удаляется путём замены значения специальным флагом^[en], показывающим, что ключ удалён. Однако такие флаги приводят к увеличению коэффициента загрузки хеш-таблицы. В этой стратегии может стать необходимым удалить флаги из массива и пересчитать хеш-значения всех оставшихся пар ключ-значение, когда слишком много значений окажутся удалёнными^[3][4].

Квадратичное зондирование

Квадратичное зондирование - это схема открытой адресации в компьютерном программировании для решения хэш-коллизии в хеш-таблицах . Квадратичное зондирование работает путем взятия исходного хеш-индекса и добавления последовательных значений произвольного квадратичного многочлена до тех пор, пока не будет найден открытый слот.

Пример последовательности с использованием квадратичного зондирования:

H + 1 2, H + 2 2, H + 3 2, H + 4 2,. . . , ЧАС + К 2 {\ Displaystyle Н + 1 ^ {2}, Н + 2 ^ {2}, Н + 3 ^ {2}, Н + 4 ^ {2}, ..., Н + k ^ {2 }}

Квадратичное зондирование может быть более эффективным алгоритмом в таблице открытой адресации , так как оно лучше позволяет избежать проблемы кластеризации, которая может возникнуть при линейном зондировании , хотя и не защищена . Он также обеспечивает хорошее кэширование памяти, поскольку сохраняет некоторую локальность ссылки ; однако линейное зондирование имеет большую локальность и, следовательно, лучшую производительность кеша.

Двойное хеширование

Двойное хеширование (англ. double hashing) — метод борьбы с коллизиями, возникающими при открытой адресации, основанный на использовании двух хеш-функций для построения различных последовательностей исследования хеш-таблицы.

Принцип двойного хеширования[править]

При двойном хешировании используются две независимые хеш-функции h1(k)h1(k) и h2(k)h2(k). Пусть kk — это наш ключ, mm — размер нашей таблицы, nmodmnmodm — остаток от деления nn на mm, тогда сначала исследуется ячейка с адресом h1(k)h1(k), если она уже занята, то рассматривается (h1(k)+h2(k))modm(h1(k)+h2(k))modm, затем (h1(k)+2⋅h2(k))modm(h1(k)+2⋅h2(k))modm и так далее. В общем случае идёт проверка последовательности ячеек (h1(k)+i⋅h2(k))modm(h1(k)+i⋅h2(k))modm где i=(0,1,...,m−1)i=(0,1,...,m−1)

Таким образом, операции вставки, удаления и поиска в лучшем случае выполняются за O(1)O(1), в худшем — за O(m)O(m), что не отличается от обычного линейного разрешения коллизий. Однако в среднем, при грамотном выборе хеш-функций, двойное хеширование будет выдавать лучшие результаты, за счёт того, что вероятность совпадения значений сразу двух независимых хеш-функций ниже, чем одной.

∀x≠y∃h1,h2:p(h1(x)=h1(y))>p((h1(x)=h1(y))∧(h2(x)=h2(y)))
Дерево и двоичная куча

Бинарное дерево — это иерархическая структура данных, в которой каждый узел имеет значение (оно же является в данном случае и ключом) и ссылки на левого и правого потомка. Узел, находящийся на самом верхнем уровне (не являющийся чьим либо потомком) называется корнем. Узлы, не имеющие потомков (оба потомка которых равны NULL) называются листьями.

Бинарное дерево поиска — это бинарное дерево, обладающее дополнительными свойствами: значение левого потомка меньше значения родителя, а значение правого потомка больше значения родителя для каждого узла дерева. То есть, данные в бинарном дереве поиска хранятся в отсортированном виде. При каждой операции вставки нового или удаления существующего узла отсортированный порядок дерева сохраняется. При поиске элемента сравнивается искомое значение с корнем. Если искомое больше корня, то поиск продолжается в правом потомке корня, если меньше, то в левом, если равно, то значение найдено и поиск прекращается.

BST (Двоичное дерево поиска)

Двоичное дерево поиска (англ. binarysearchtree, BST) — двоичное дерево, для которого выполняются следующие дополнительные условия (свойства дерева поиска):

оба поддерева — левое и правое — являются двоичными деревьями поиска;
у всех узлов левого поддерева произвольного узла X значения ключей данных меньше, нежели значение ключа данных самого узла X;
у всех узлов правого поддерева произвольного узла X значения ключей данных больше либо равны, нежели значение ключа данных самого узла X.

Очевидно, данные в каждом узле должны обладать ключами, на которых определена операция сравнения меньше.

Как правило, информация, представляющая каждый узел, является записью, а не единственным полем данных. Однако это касается реализации, а не природы двоичного дерева поиска.

Для целей реализации двоичное дерево поиска можно определить так:

Двоичное дерево состоит из узлов (вершин) — записей вида (data, left, right), где data — некоторые данные, привязанные к узлу, left и right — ссылки на узлы, являющиеся детьми данного узла — левый и правый сыновья соответственно. Для оптимизации алгоритмов конкретные реализации предполагают также определения поля parent в каждом узле (кроме корневого) — ссылки на родительский элемент.
Данные (data) обладают ключом (key), на котором определена операция сравнения «меньше». В конкретных реализациях это может быть пара (key, value) — (ключ и значение), или ссылка на такую пару, или простое определение операции сравнения на необходимой структуре данных или ссылке на неё.
Для любого узла X выполняются свойства дерева поиска: key[left[X]] < key[X] ≤ key[right[X]], то есть ключи данных родительского узла больше ключей данных левого сына и нестрого меньше ключей данных правого.

Сбалансированные деревья

АВЛ-деревом называется такое дерево поиска, в котором для любого его узла высоты левого и правого поддеревьев отличаются не более, чем на 1. Эта структура данных разработана советскими учеными Адельсон-Вельским Георгием Максимовичем и Ландисом Евгением Михайловичем в 1962 году. Аббревиатура АВЛ соответствует первым буквам фамилий этих ученых. Первоначально АВЛ-деревья были придуманы для организации перебора в шахматных программах. Советская шахматная программа «Каисса» стала первым официальным чемпионом мира в 1974 году. В каждом узле АВЛ-дерева, помимо ключа, данных и указателей на левое и правое поддеревья (левого и правого сыновей), хранится показатель баланса – разность высот правого и левого поддеревьев. В некоторых реализациях этот показатель может вычисляться отдельно в процессе обработки дерева тогда, когда это необходимо.

Дерево выражений

Основы

Для начала необходимо разобраться с деревьями выражений. Под ними понимают тип Expression или любой из его наследников (о них речь пойдет позже). При обычном раскладе выражение/алгоритмы представляются в виде выполняемого кода/инструкций, с которыми пользователь может не так и много чего делать (в основном выполнять). Тип Expression позволяет представить выражение/алгоритм (как правило лямбды, но не обязательно) как данные, организованные в виде древовидной структуры, к которой пользователь имеет доступ. Древовидный способ организации информации об алгоритме и название класса и дают нам «деревья выражений».

Для понятности разберем простой пример. Допустим, у нас есть лямбда

(х) => Console.WriteLine(х + 5)

Это можно представить в виде следующего дерева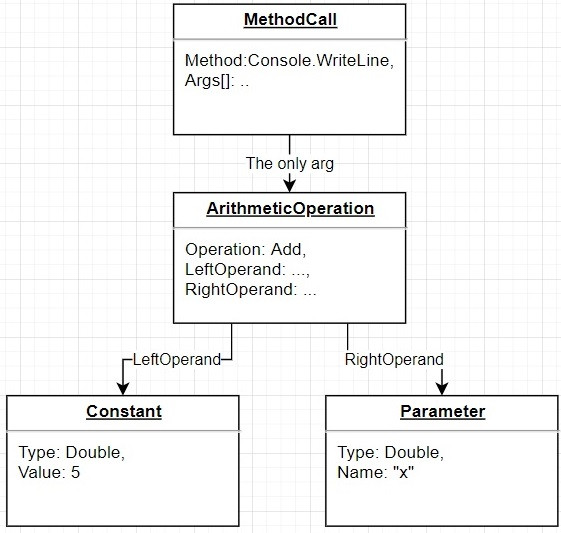

Корень дерева — вершина "MethodCall", параметры метода — также выражения, следовательно может иметь сколько угодно потомков.

В нашем случае потомок один — вершина "ArithmeticOperation". В ней содержится информация о том, какая конкретно это операция и левый и правый операнды — также выражения. У такой вершины будет всегда 2 потомка.

Операнды представлены константой (Constant) и параметром (Parameter). У таких выражений нет потомков.

Это очень упрощенные примеры, но полностью отражающие суть.

Основная особенность деревьев выражений — это то, что их можно парсить и вычитывать всю необходимую информацию о том, что алгоритм должен делать. С какой-то точки зрения, это противоположность атрибутам. Атрибуты — средство декларативного описания поведения (очень условно, но конечная цель примерно такая). В то время как деревья выражений — использование функции/алгоритма для описания данных.

Используются они, например, в провайдерах entity framework. Применение очевидно — распарсить дерево выражений, понять, что там должно выполниться и составить по этому описанию SQL. Из менее известных примеров — библиотека для мокинга moq. Деревья выражений также нашли применение в DLR (dynamic language runtime). Разработчики компилятора используют их при обеспечении совместимости между динамической природой и dotnet, вместо генерации MSIL.

Также стоит упомянуть, что деревья выражений неизменяемы.

Синтаксис

Следующее, что стоит обговорить — синтаксис. Существуют 2 основных способа:

Создание деревьев выражений через статические методы класса Expression
Использование лямбда выражения, компилирующееся в Expression

Статические методы класса Expression

Создание деревьев выражений через статические методы класса Expression используется реже (в особенности с пользовательской точки зрения). Это громоздко, но довольно просто, в нашем
распоряжении множество базовых кирпичиков, из которых можно построить довольно сложные
вещи. Создание происходит через статические методы, т.к. конструкторы выражений имеют модификатор internal. И это не означает, что нужно расчехлять рефлексию.

Красно-чёрное дерево.

Красно-чёрное дерево (англ. red-blacktree, RBtree) — один из видов самобалансирующихся двоичных деревьев поиска, гарантирующих логарифмический рост высоты дерева от числа узлов и позволяющее быстро выполнять основные операции дерева поиска: добавление, удаление и поиск узла. Сбалансированность достигается за счёт введения дополнительного атрибута узла дерева — «цвета». Этот атрибут может принимать одно из двух возможных значений — «чёрный» или «красный».

Изобретателем красно-чёрного дерева считают немца Рудольфа Байера. Название «красно-чёрное дерево» структура данных получила в статье Л. Гимбаса и Р. Седжвика (1978). По словам Гимбаса, они использовали ручки двух цветов^[1]. По словам Седжвика, красный цвет лучше всех смотрелся на лазерном принтере^[1][2].

Красно-чёрное дерево используется для организации сравнимых данных, таких как фрагменты текста или числа. Листовые узлы красно-чёрных деревьев не содержат данных, благодаря чему не требуют выделения памяти — достаточно записать в узле-предке в качестве указателя на потомка нулевой указатель. Однако в некоторых реализациях для упрощения алгоритма могут использоваться явные листовые узлы.

Красно-чёрное дерево — двоичное дерево поиска, в котором каждый узел имеет атрибут цвета. При этом:

Узел может быть либо красным, либо чёрным и имеет двух потомков;
Корень — как правило чёрный. Это правило слабо влияет на работоспособность модели, так как цвет корня всегда можно изменить с красного на чёрный;
Все листья, не содержащие данных — чёрные.
Оба потомка каждого красного узла — чёрные.
Любой простой путь от узла-предка до листового узла-потомка содержит одинаковое число чёрных узлов.

Благодаря этим ограничениям путь от корня до самого дальнего листа не более чем вдвое длиннее, чем до самого ближнего, и дерево примерно сбалансировано. Операции вставки, удаления и поиска требуют в худшем случае времени, пропорционального длине дерева, что позволяет красно-чёрным деревьям быть более эффективными в худшем случае, чем обычные двоичные деревья поиска.

Двоичная куча

Двои́чная ку́ча, пирами́да^[1], или сортиру́ющее де́рево — такое двоичное дерево, для которого выполнены три условия:

Значение в любой вершине не меньше, чем значения её потомков^{[К 1]}.
Глубина всех листьев (расстояние до корня) отличается не более чем на 1 слой.
Последний слой заполняется слева направо без «дырок».

Существуют также кучи, где значение в любой вершине, наоборот, не больше, чем значения её потомков. Такие кучи называются min-heap, а кучи, описанные выше — max-heap. В дальнейшем рассматриваются только max-heap. Все действия с min-heap осуществляются аналогично.

Двоичная куча представляет собой полное бинарное дерево, для которого выполняется основное свойство кучи: приоритет каждой вершины больше приоритетов её потомков. В простейшем случае приоритет каждой вершины можно считать равным её значению. В таком случае структура называется max-heap, поскольку корень поддерева является максимумом из значений элементов поддерева. В этой статье для простоты используется именно такое представление. Напомню также, что дерево называется полным бинарным, если у каждой вершины есть не более двух потомков, а заполнение уровней вершин идет сверху вниз (в пределах одного уровня – слева направо).

Графы и графовые алгоритмы

Граф состоит из конечного множества вершин (узлов) и набора рёбер, соединяющих эти вершины. Две вершины считаются смежными, если они соединены друг с другом одним и тем же ребром.

Ниже приведён ряд базовых понятий, относящихся к графам. Они проиллюстрированы примерами на рисунке 1.

Порядок: число вершин в графе.
Размер: число рёбер в графе.
Степень вершины: число рёбер, инцидентных вершине.
Изолированная вершина: вершина, которая не связана ни с одной другой вершиной графа.
Петля: ребро, вершины которого совпадают.
Ориентированный граф: граф, в котором все рёбра имеют направление, определяющее начальную и конечную вершину.
Неориентированный граф: граф с рёбрами, которые не имеют направления.
Взвешенный граф: рёбра такого графа имеют определённый вес.
Невзвешенный граф: рёбра такого графа не имеют никаких весов.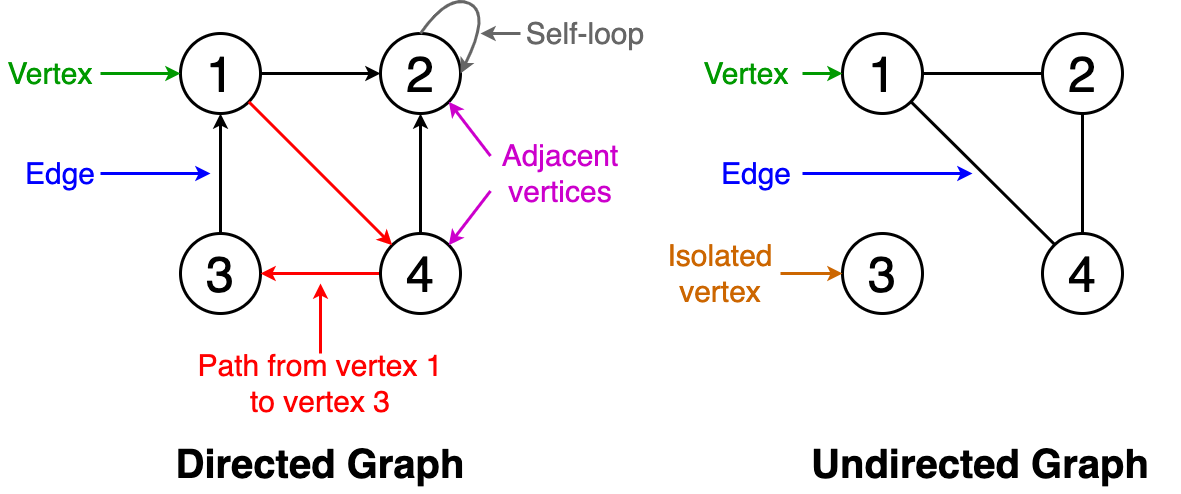

Рис. 1. Терминология графов (схематичное изображение)

Поиск в глубину (BFS)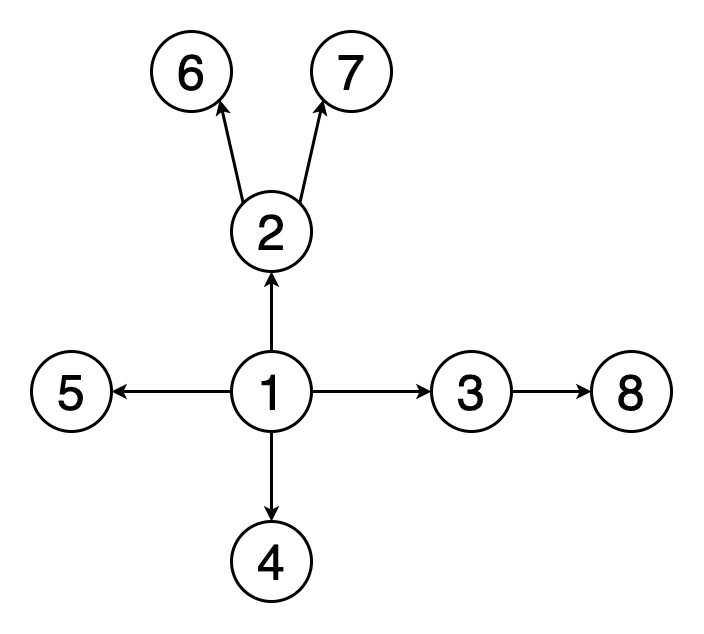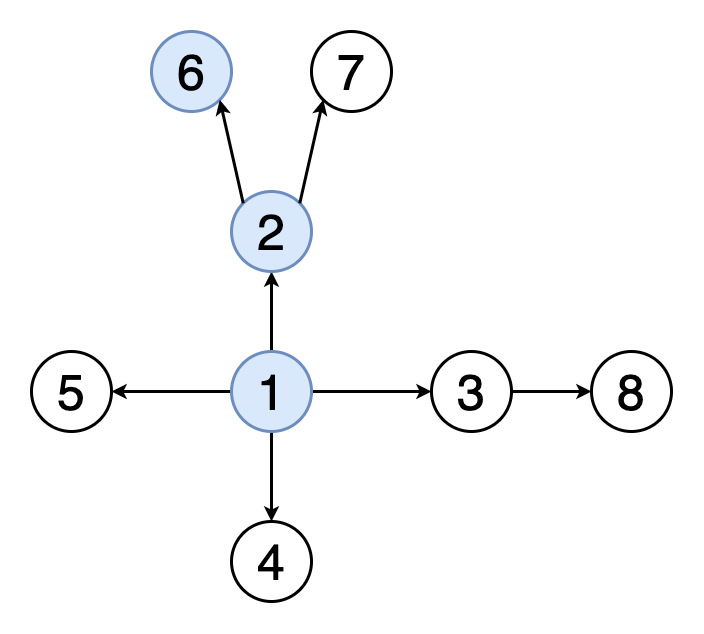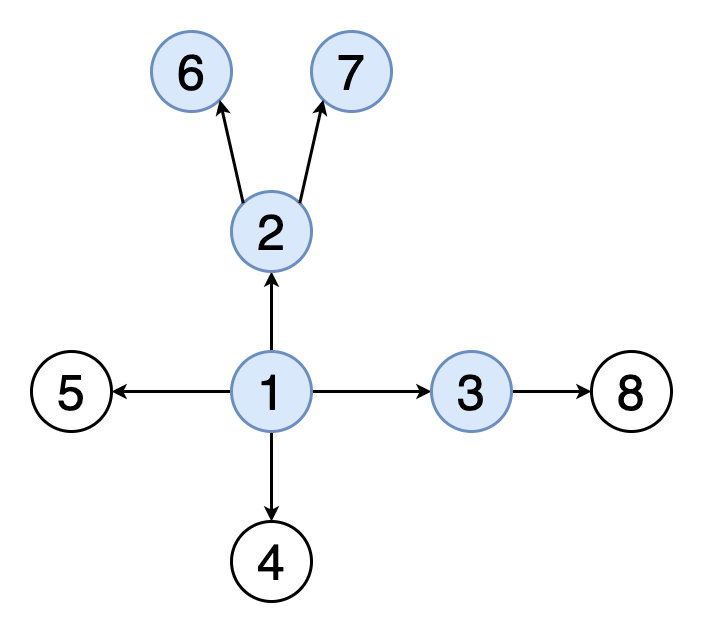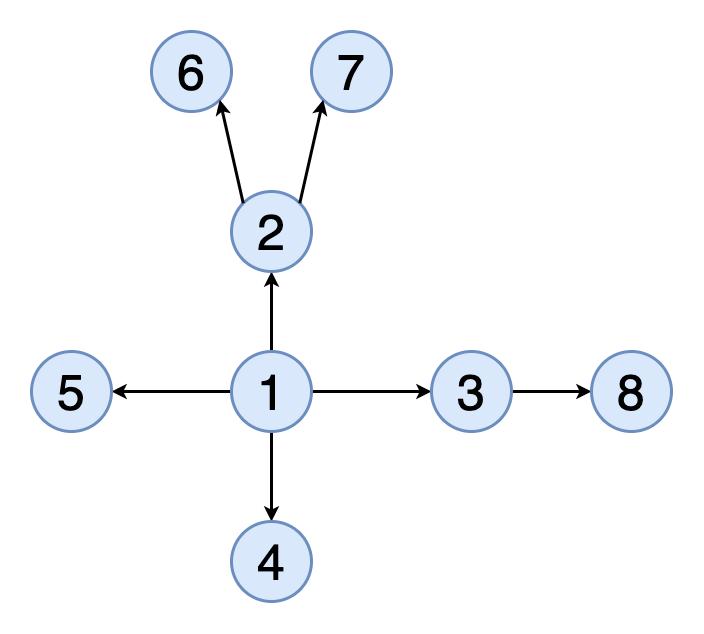

Рис. 3. Визуальное отображение обхода на графах (поиск в глубину)

Поиск в глубину начинается с определённой вершины, затем уходит как можно дальше вдоль каждой ветви и возвращается обратно. Здесь тоже необходимо отслеживать посещённые алгоритмом вершины. Для того, чтобы стало возможным возвращение обратно, при реализации алгоритма поиска в глубину используется структура данных «стек».

На рисунке 3 показан пример того, как выглядит поиск в глубину на том же графе, который использован на рисунке 2. Граф обходится на всю глубину каждой ветви с возвращением обратно.

1 2 3 4 5 6 7 8 9 10 11