Алгоритм и структура данных. 1 Базовый процедурноориентированный алгоритмический язык

• Название: 1 Базовый процедурноориентированный алгоритмический язык
• Анкор: Алгоритм и структура данных
• Дата: 03.11.2022
• Размер: 1.16 Mb.
• Имя файла: Алгоритм и структура данных.docx
• Тип: Документы; #768957
• страница: 9 из 11

Классификация списков

По количеству полей указателей различают однонаправленный (односвязный) и двунаправленный (двусвязный) списки.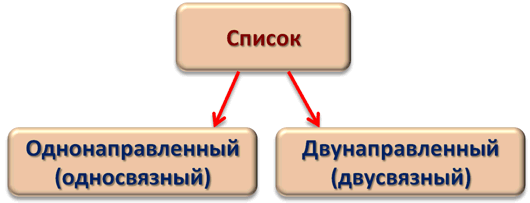


Связный список, содержащий только один указатель на следующий элемент, называется односвязным.
Связный список, содержащий два поля указателя – на следующий элемент и на предыдущий, называется двусвязным.

По способу связи элементов различают линейные и циклические списки.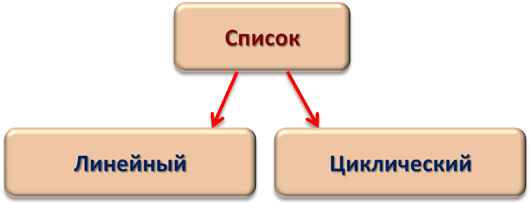


Связный список, в котором, последний элемент указывает на NULL, называется линейным.
Связный список, в котором последний элемент связан с первым, называется циклическим.

Виды списков

Таким образом, различают 4 основных вида списков.

• 
  Односвязный линейный список (ОЛС).
  Каждый узел ОЛС содержит 1 поле указателя на следующий узел. Поле указателя последнего узла содержит нулевое значение (указывает на NULL).
  
  
• 
  Односвязный циклический список (ОЦС).
  Каждый узел ОЦС содержит 1 поле указателя на следующий узел. Поле указателя последнего узла содержит адрес первого узла (корня списка).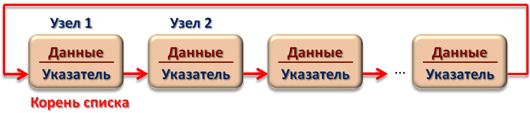
  
  
• 
  Двусвязный линейный список (ДЛС).
  Каждый узел ДЛС содержит два поля указателей: на следующий и на предыдущий узел. Поле указателя на следующий узел последнего узла содержит нулевое значение (указывает на NULL). Поле указателя на предыдущий узел первого узла (корня списка) также содержит нулевое значение (указывает на NULL).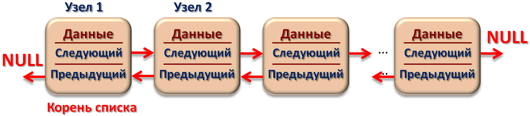
  
  
• 
  Двусвязный циклический список (ДЦС).
  Каждый узел ДЦС содержит два поля указателей: на следующий и на предыдущий узел. Поле указателя на следующий узел последнего узла содержит адрес первого узла (корня списка). Поле указателя на предыдущий узел первого узла (корня списка) содержит адрес последнего узла.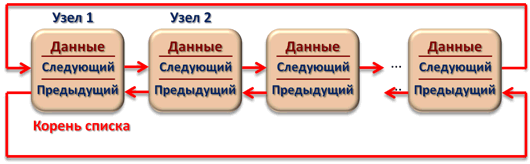
  
  

Хеш таблицы и Хеш функции

Хеш-табли́ца (англ. hash-table) — структура данных, реализующая интерфейс ассоциативного массива. В отличие от деревьев поиска, реализующих тот же интерфейс, обеспечивают меньшее время отклика в среднем. Представляет собой эффективную структуру данных для реализации словарей, а именно, она позволяет хранить пары (ключ, значение) и выполнять три операции: операцию добавления новой пары, операцию поиска и операцию удаления пары по ключу.

Хеш-таблица (hash table) — это специальная структура данных для хранения пар ключей и их значений. По сути это ассоциативный массив, в котором ключ представлен в виде хеш-функции.

Чтобы разобраться, что такое хеш-таблицы, представьте, что вас попросили создать библиотеку и заполнить ее книгами. Но вы не хотите заполнять шкафы в произвольном порядке.

Первое, что приходит в голову — разместить все книги в алфавитном порядке и записать все в некий справочник. В этом случае не придется искать нужную книгу по всей библиотеке, а только по справочнику.

А можно сделать еще удобнее. Если изначально отталкиваться от названия книги или имени автора, то лучше использовать некий алгоритм хеширования, который обрабатывает входящее значение и выдает номер шкафа и полки для нужной книги.

Зная этот алгоритм хэширования, вы быстро найдете нужную книгу по ее названию.

Учтите, что хеш-функция должна иметь следующие свойства:

• 
  Всегда возвращать один и тот же адрес для одного и того же ключа;
  
• 
  Не обязательно возвращает разные адреса для разных ключей;
  
• 
  Использует все адресное пространство с одинаковой вероятностью;
  
• 
  Быстро вычислять адрес.
  

Борьба с коллизиями (они же столкновения)

В идеальном случае, когда заранее известны все пары ключ-значение, достаточно легко реализовать идеальную хеш-таблицу, в которой время поиска будет постоянным (используется идеальная хеш-функция, которая определяет положения в таблице по целым значениям и без столкновений).

Но в большинстве случаев приходится бороться с коллизиями. Обычно применяются методы цепочек и открытой индексации.

Хеширование (англ. hashing) — класс методов поиска, идея которого состоит в вычислении хеш-кода, однозначно определяемого элементом с помощью хеш-функции, и использовании его, как основы для поиска (индексирование в памяти по хеш-коду выполняется за O(1)O(1)). В общем случае, однозначного соответствия между исходными данными и хеш-кодом нет в силу того, что количество значений хеш-функций меньше, чем вариантов исходных данных, поэтому существуют элементы, имеющие одинаковые хеш-коды — так называемые коллизии, но если два элемента имеют разный хеш-код, то они гарантированно различаются. Вероятность возникновения коллизий играет немаловажную роль в оценке качества хеш-функций. Для того чтобы коллизии не замедляли работу с таблицей существуют методы для борьбы с ними.

Хеш-функция 

Хеш-функция (англ. hashfunction от hash — «превращать в фарш», «мешанина»^[1]), или функция свёртки — функция, осуществляющая преобразование массива входных данных произвольной длины в выходную битовую строку установленной длины, выполняемое определённым алгоритмом. Преобразование, производимое хеш-функцией, называется хешированием. Исходные данные называются входным массивом, «ключом» или «сообщением». Результат преобразования называется «хешем», «хеш-кодом», «хеш-суммой», «сводкой сообщения».

Хеш-функции применяются в следующих случаях:

• 
  при построении ассоциативных массивов;
  
• 
  при поиске дубликатов в последовательностях наборов данных;
  
• 
  при построении уникальных идентификаторов для наборов данных;
  
• 
  при вычислении контрольных сумм от данных (сигнала) для последующего обнаружения в них ошибок (возникших случайно или внесённых намеренно), возникающих при хранении и/или передаче данных;
  
• 
  при сохранении паролей в системах защиты в виде хеш-кода (для восстановления пароля по хеш-коду требуется функция, являющаяся обратной по отношению к использованной хеш-функции);
  
• 
  при выработке электронной подписи (на практике часто подписывается не само сообщение, а его «хеш-образ»);
  
• 
  и др.
  

В общем случае (согласно принципу Дирихле) нет однозначного соответствия между хеш-кодом и исходными данными. Возвращаемые хеш-функцией значения менее разнообразны, чем значения входного массива. Случай, при котором хеш-функция преобразует более чем один массив входных данных в одинаковые сводки, называется «коллизией». Вероятность возникновения коллизий используется для оценки качества хеш-функций.

Существует множество алгоритмов хеширования, различающихся различными свойствами. Примеры свойств:

• 
  разрядность;
  
• 
  вычислительная сложность;
  
• 
  криптостойкость.
  
• 
  Криптографическая хеш-функция - это математический алгоритм, который отображает данные произвольного размера в битовый массив фиксированного размера.
  
• 
  Результат, производимый хеш-функцией, называется «хеш-суммой» или же просто «хешем», а входные данные часто называют «сообщением».
  
• 
  Для идеальной хеш-функции выполняются следующие условия:
  
• 
  а) хеш-функция является детерминированной, то есть одно и то же сообщение приводит к одному и тому же хеш-значению
  b) значение хеш-функции быстро вычисляется для любого сообщения
  c) невозможно найти сообщение, которое дает заданное хеш-значение
  d) невозможно найти два разных сообщения с одинаковым хеш-значением
  e) небольшое изменение в сообщении изменяет хеш настолько сильно, что новое и старое значения кажутся некоррелирующими
  

Производительность хеш-таблицы

Производительность хэш-таблиц: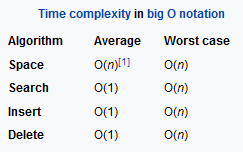


Дизайн хеш-функций

Строительство Меркле-Дамгарда

Основная статья: Строительство Меркла-Дамгарда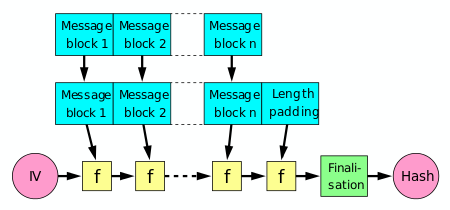



Хэш-конструкция Меркла – Дамгарда

Хеш-функция должна иметь возможность обрабатывать сообщение произвольной длины в вывод фиксированной длины. Этого можно достичь, разбив входные данные на серию блоков одинакового размера и последовательно работая с ними, используя функцию одностороннего сжатия . Функция сжатия может быть либо специально разработана для хеширования, либо построена на основе блочного шифра. Хеш-функция, построенная с помощью конструкции Меркла-Дамгарда, так же устойчива к столкновениям, как и ее функция сжатия; любая коллизия для полной хэш-функции может быть прослежена до коллизии в функции сжатия.

Последний обработанный блок также должен быть однозначно дополнен по длине ; это имеет решающее значение для безопасности этой конструкции. Эта конструкция называется конструкцией Меркла – Дамгарда . Наиболее распространенные классические хеш-функции, включая SHA-1 и MD5, принимают эту форму.

Широкая труба против узкой трубы

Прямое применение конструкции Меркла-Дамгарда, где размер выходных данных хеш-функции равен размеру внутреннего состояния (между каждым этапом сжатия), приводит к узкой конвейерной схеме хеширования. Эта конструкция вызывает множество врожденных недостатков, включая увеличение длины, множественные коллизии, атаки с длинными сообщениями, атаки с генерацией и вставкой, а также не может быть распараллелена. В результате, современные функции хеширования построены на широкоэкранном трубных конструкций, которые имеют больший размер внутреннего состояния - которые варьируются от щипков в строительстве Merkle-Damgård новых конструкций, таких как строительство губки и строительство HAIFA . Ни один из участников конкурса хэш-функций NIST не использует классическую конструкцию Меркла – Дамгарда.

Между тем, усечение вывода более длинного хэша, например, используемого в SHA-512/256, также предотвращает многие из этих атак.

Схемы разрешения столкновений: отдельная цепочка, открытая адресация, линейное зондирование, квадратичное зондирование, двойное хеширование

Хэш-коллизии практически неизбежны при хэшировании случайного подмножества большого набора возможных ключей. Например, если 2450 ключей хэшируются в миллион корзин (buckets), даже при совершенно равномерном случайном распределении, в соответствии с проблемой дня рождения, существует приблизительно 95% вероятность того, что по крайней мере два ключа будут хэшированы в один и тот же слот.

Поэтому почти все реализации хэш-таблиц имеют некоторую стратегию разрешения коллизий для обработки таких событий. Некоторые общие стратегии описаны ниже. Все эти методы требуют, чтобы ключи (или указатели на них) были сохранены в таблице вместе со связанными значениями.

Отдельная цепочка

Отдельная цепочка



В методе, известном как отдельная цепочка, каждая корзина (bucket) независима и имеет своего рода список записей с одинаковым индексом. Время для операций с хэш-таблицами - это время нахождения корзины (bucket) (которое является постоянным) плюс время для операции со списком.

В хорошей хэш-таблице каждая корзина (bucket) имеет ноль или одну запись, а иногда две или три, но редко больше. Поэтому структуры, которые эффективны во времени и пространстве для этих случаев, являются предпочтительными. Структуры, которые эффективны для довольно большого количества записей на корзину, не нужны или нежелательны. Если такие случаи случаются часто, хэширующая функция должна быть исправлена.

Отдельное сцепление со связанными списками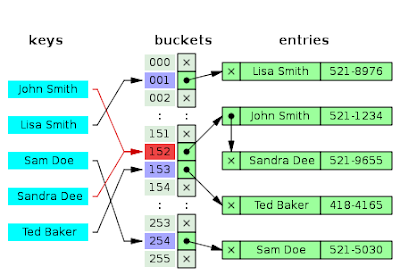

Связанные хэш-таблицы со связанными списками популярны, потому что они требуют только базовых структур данных с простыми алгоритмами и могут использовать простые хэш-функции, которые не подходят для других методов.

Открытая адресация

Метод открытой адресации предполагает несколько иной подход.
Имеется обычная хеш-таблице. В процессе ее заполнения, при получении нового значения, мы его заносим в том случае, если данная ячейка еще не заполнена (например, значение равно нулю). В противном случае предполагается занесение значения в другую ячейку, вычисляемую по какому-либо алгоритму, но если и она оказывается уже заполненной, то вычисляется еще одна ячейка и т.д.
Очевидно, что на самом деле существует столько конкретных методов открытой адресации, сколько алгоритмов перевычисления ячеек можно предложить.
Один из таких подходов называется методом линейных проб. Этот метод предполагает для вычисления заполняемой ячейки в случае коллизии использование функций:
 

h(x)=x mod q + 1; hi(x) = (x+1) mod q + 1; h₂(x) = (x+2) mod q + 1; h₃(x) = (x+3) mod q + 1;

То есть, попросту говоря, если вычисленная ячейка оказалась занятой, то ис­пользуем соседнюю ячейку справа и т.д., при этом для последней ячейки роль со­седней справа выполняет первая ячейка. При поиске, кроме текущего значения, следует просматривать и ячейки справа от текущей до тех пор, пока мы не достиг­нем пустой ячейки.

Очевидно, что эффективность метода тем выше, чем меньше ячеек прихо­дится просмотреть при заполнении и поиске. Метод линейной адресации оказыва­ется неэффективным, так как данные часто имеют свойства группироваться вокруг определенных значений. Например, возраст преподавателей, может группи­роваться либо в пределах 50-60 лет, либо 25-30 лет, и подобные закономерности часты. Таким образом, при переадресации внутри хеш-таблицы следует стремить­ся к максимальному расширению области затрагиваемых ячеек.

Метод квадратичных проб состоит в том, что если возникает коллизия, ис­пользуем функции

h(x)=x mod q + 1; h₁(x) = (x+1) mod q + 1; h₂(x) = (x+2²) mod q + 1; h₃(x) = (x+3²) mod q + 1;

Здесь обязательно выполнение условия «простоты» числа q, иначе алгоритм, как доказано, может зациклить. Этот метод устраняет основной недостаток метода линейных проб и является наиболее часто используемым.

Линейное зондирование

Линейное зондирование — это схема в программировании для разрешения коллизий в хеш-таблицах, структурах данных для управления наборами пар ключ – значение^[en] и поиска значений, ассоциированных с данным ключом. Схему придумали в 1954 Джин Амдал, Элейн Макгроу^[en] и Артур Сэмюэл, а проанализировна она была в 1963 Дональдом Кнутом.

Вместе с квадратичным зондированием^[en] и двойным зондированием^[en] линейное зондирование является видом открытой адресации^[en]. В этих схемах каждая ячейка хеш-таблицы содержит одну пару ключ-значение. Если хеш-функция даёт коллизию, отображая значение нового ключа в ячейку хеш-таблицы, занятую другим ключом, линейное зондирование просматривает таблицу до ближайшей свободной следующей ячейки и вставляет новый ключ туда. Поиск значения осуществляется тем же образом, путём просмотра таблицы последовательно, начиная с позиции, определённой хеш-функцией, пока не найдёт совпадение ключа, либо пустую ячейку.

Все элементы хранятся непосредственно в хеш-таблице, без использования связных списков. В отличие от хеширования с цепочками, при использовании этого метода может возникнуть ситуация, когда хеш-таблица окажется полностью заполненной, следовательно, будет невозможно добавлять в неё новые элементы. Так что при возникновении такой ситуации решением может быть динамическое увеличение размера хеш-таблицы, с одновременной её перестройкой.

Стратегии поиска[править]

Последовательный поиск

При попытке добавить элемент в занятую ячейку ii начинаем последовательно просматривать ячейки i+1,i+2,i+3i+1,i+2,i+3 и так далее, пока не найдём свободную ячейку. В неё и запишем элемент.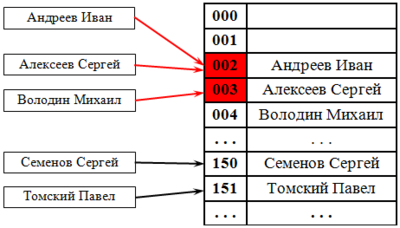



Линейный поиск

Выбираем шаг qq. При попытке добавить элемент в занятую ячейку ii начинаем последовательно просматривать ячейки i+(1⋅q),i+(2⋅q),i+(3⋅q)i+(1⋅q),i+(2⋅q),i+(3⋅q) и так далее, пока не найдём свободную ячейку. В неё и запишем элемент. По сути последовательный поиск - частный случай линейного, где q=1q=1.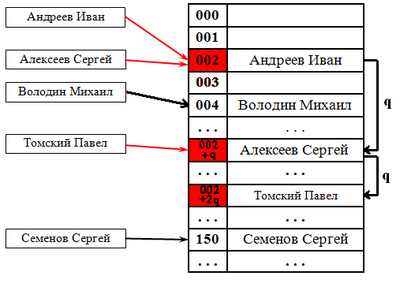



Квадратичный поиск

Шаг qq не фиксирован, а изменяется квадратично: q=1,4,9,16...q=1,4,9,16.... Соответственно при попытке добавить элемент в занятую ячейку ii начинаем последовательно просматривать ячейки i+1,i+4,i+9i+1,i+4,i+9 и так далее, пока не найдём свободную ячейку.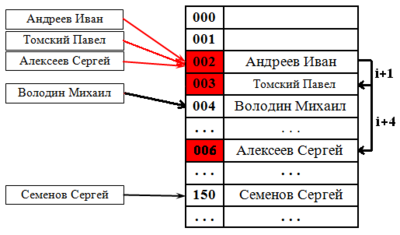

Проверка наличия элемента в таблице[править]

Проверка осуществляется аналогично добавлению: мы проверяем ячейку ii и другие, в соответствии с выбранной стратегией, пока не найдём искомый элемент или свободную ячейку.

При поиске элемента может получится так, что мы дойдём до конца таблицы. Обычно поиск продолжается, начиная с другого конца, пока мы не придём в ту ячейку, откуда начинался поиск.

Проблемы данных стратегий[править]

Проблем две — крайне нетривиальное удаление элемента из таблицы и образование кластеров — последовательностей занятых ячеек.

Кластеризация замедляет все операции с хеш-таблицей: при добавлении требуется перебирать всё больше элементов, при проверке тоже. Чем больше в таблице элементов, тем больше в ней кластеры и тем выше вероятность того, что добавляемый элемент попадёт в кластер. Для защиты от кластеризации используется двойное хеширование и хеширование кукушки.

Удаление элемента без пометок[править]

Рассуждение будет описывать случай с линейным поиском хеша. Будем при удалении элемента сдвигать всё последующие на qq позиций назад. При этом:

• 
  если в цепочке встречается элемент с другим хешем, то он должен остаться на своём месте (такая ситуация может возникнуть если оставшаяся часть цепочки была добавлена позже этого элемента)
  
• 
  в цепочке не должно оставаться "дырок", тогда любой элемент с данным хешем будет доступен из начала цепи
  

Учитывая это будем действовать следующим образом: при поиске следующего элемента цепочки будем пропускать все ячейки с другим значением хеша, первый найденный элемент копировать в текущую ячейку, и затем рекурсивно его удалять. Если такой следующей ячейки нет, то текущий элемент можно просто удалить, сторонние цепочки при этом не разрушатся (чего нельзя сказать про случай квадратичного поиска).