|
|
Алгоритм и структура данных. 1 Базовый процедурноориентированный алгоритмический язык
Применяется:
Поиск в ширину (DFS)
Обход или поиск — это одна из фундаментальных операций, выполняемых на графах. Поиск в ширину начинается с определённой вершины, затем исследуются все её соседи на данной глубине и происходит переход к вершинам следующего уровня. В графах, в отличие от деревьев, могут быть циклы — пути, в которых первая и последняя вершины совпадают. Поэтому необходимо отслеживать посещённые алгоритмом вершины. При реализации алгоритма поиска в ширину используется структура данных «очередь».
На рисунке 2 показан пример того, как выглядит поиск в ширину на графе. Жёлтым цветом помечаются обнаруженные вершины, красным — посещённые.
Применяется для:
определения кратчайших путей и минимальных остовных деревьев;
индексации веб-страниц поисковыми ботами;
поиска в соцсетях;
нахождения доступных соседних узлов в одноуровневых сетях, таких как BitTorrent.
Кратчайший путь
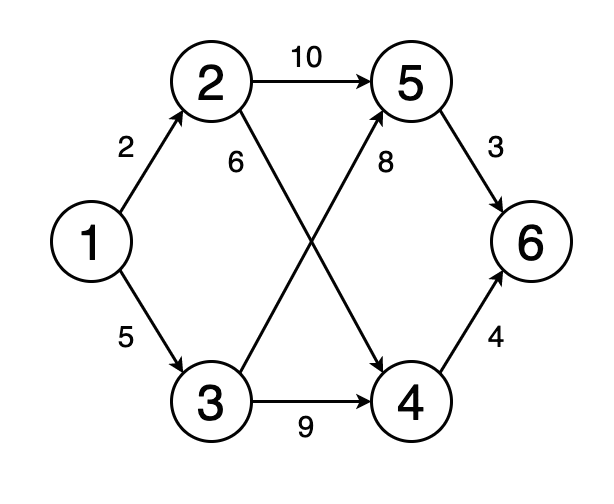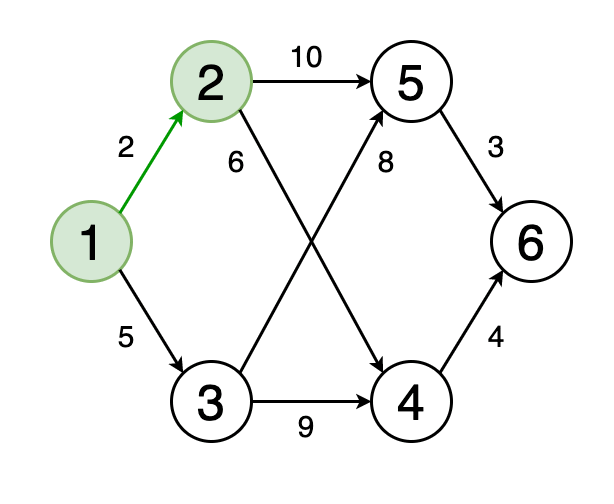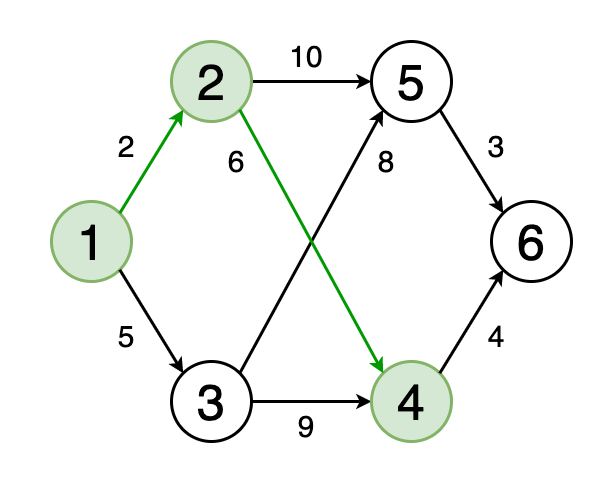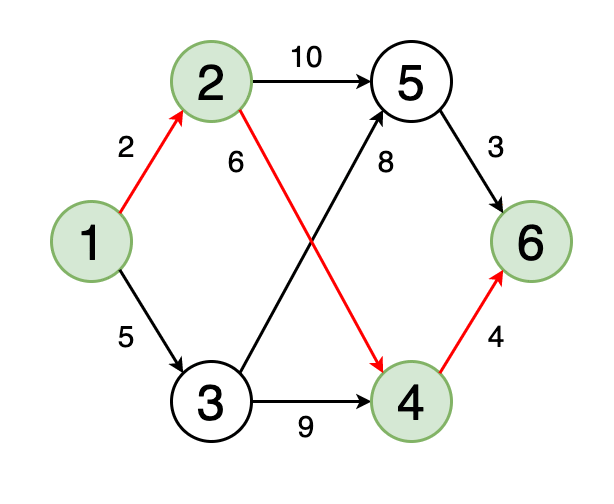
Рис. 4. Визуальное отображение кратчайшего пути от вершины 1 к вершине 6
Кратчайший путь от одной вершины графа к другой — это путь, при котором сумма весов рёбер, его составляющих, должна быть минимальна.
На рисунке 4 показан кратчайший путь на графе от вершины 1 до вершины 6.
Алгоритмы нахождения кратчайшего пути:
Алгоритм Дейкстры.
https://ru.wikipedia.org/wiki/Алгоритм_Дейкстры#Формулировка_задачи
https://prog-cpp.ru/deikstra/
Алгоритм Беллмана-Форда. https://medium.com/nuances-of-programming/наглядное-объяснение-алгоритма-беллмана-форда-775a32db3c77#:
:text=Алгоритм%20Беллмана-Форда%20находит%20в,в%20таблице%20в%20алфавитном%20порядке.
Применяются в:
картографических сервисах типа Google maps или Apple maps для прокладки маршрутов и определения местоположения;
сетях для решения проблемы минимальной задержки пути;
абстрактных автоматах для определения через переход между различными состояниями возможных вариантов достижения некоторого целевого состояния, например минимально возможного количества ходов, необходимого для победы в игре.
Обнаружение циклов
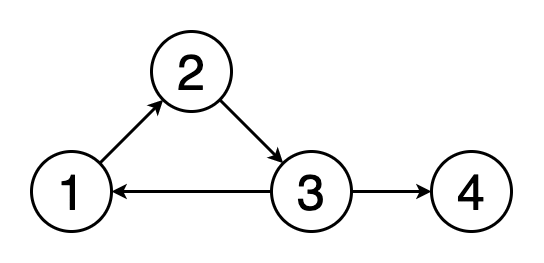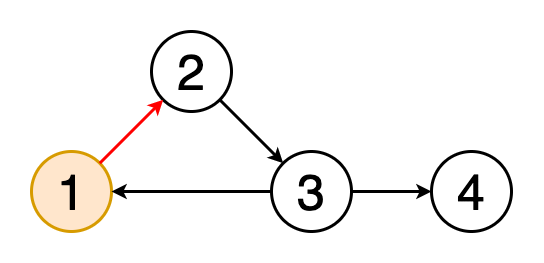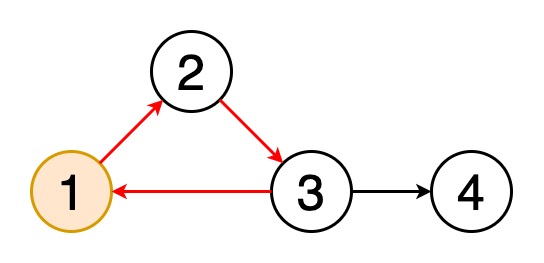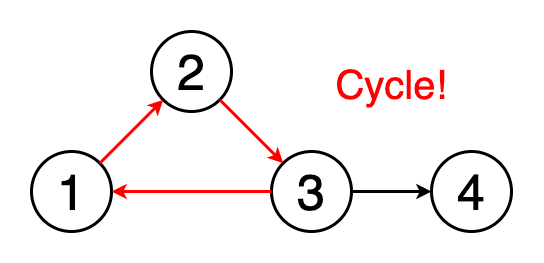
Рис. 5. Цикл
Цикл — это путь, в котором первая и последняя вершины графа совпадают. То есть путь, начинающийся и завершающийся в одной и той же вершине, называется циклом. Обнаружение циклов — это процесс выявления таких циклов. На рисунке 5 показано, как происходит обнаружение цикла.
Алгоритмы обнаружения цикла:
Алгоритм Флойда. https://foxford.ru/wiki/informatika/algoritm-floyda
Алгоритм Брента.
Применяются:
в распределённых алгоритмах, использующих сообщения;
для обработки крупных графов с использованием распределённой системы обработки в кластере;
для обнаружения взаимоблокировок в системах с параллельным выполнением;
в криптографических приложениях для выявления ключей сообщения, которые могут соответствовать одному и тому же зашифрованному значению.
Минимальное остовное дерево
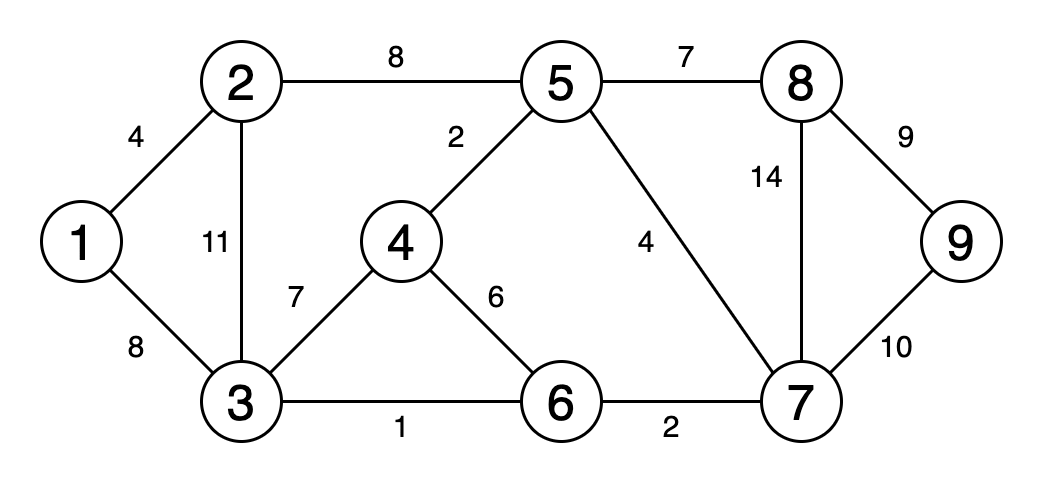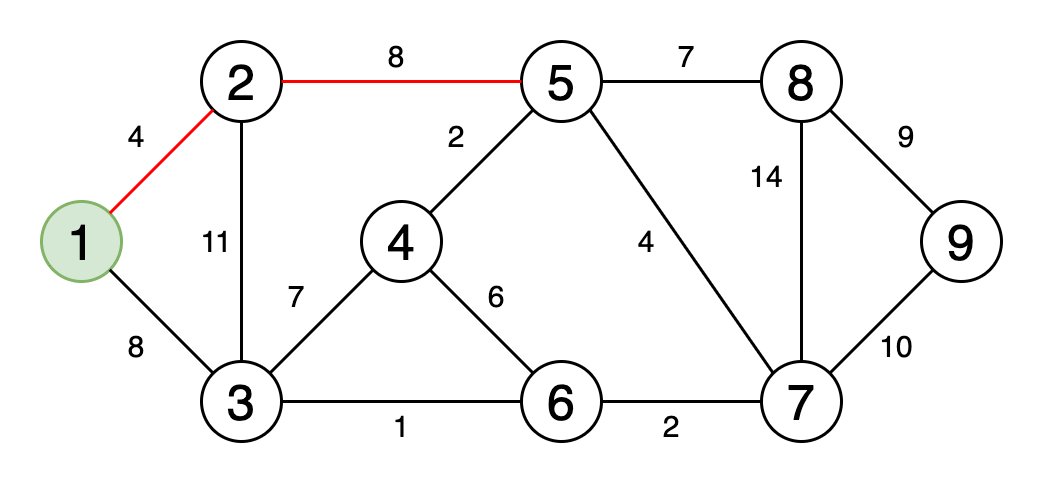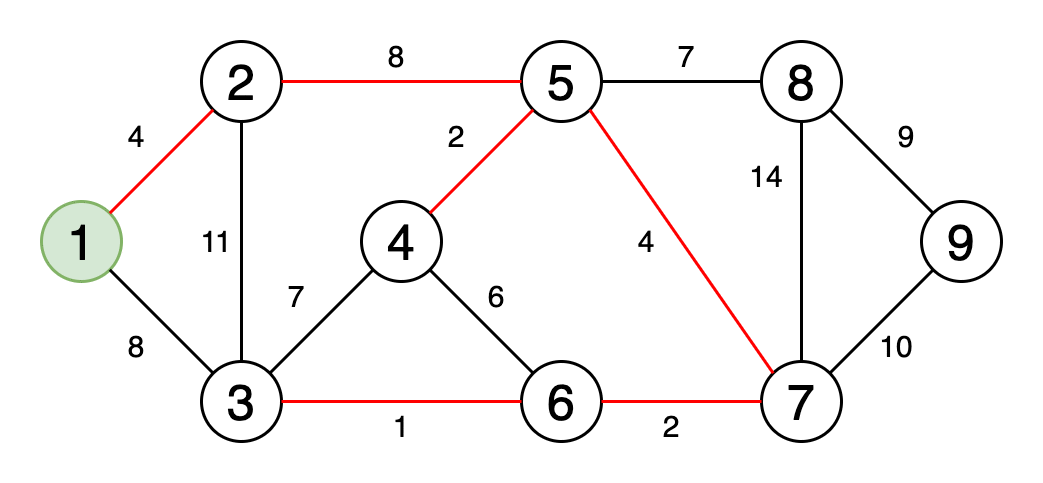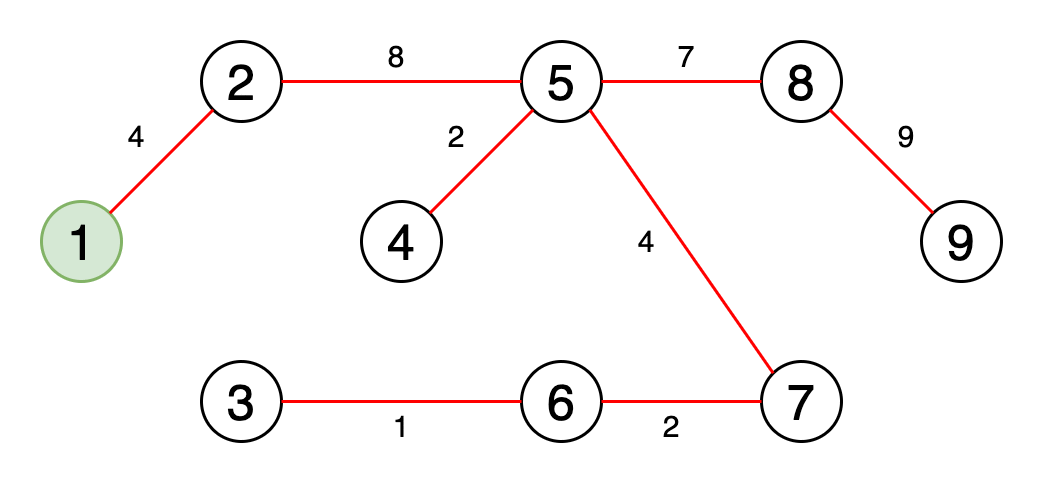
Рис. 6. Визуальное отображение минимального остовного дерева
Минимальное остовное дерево — это подмножество рёбер графа, которое соединяет все вершины, имеющие минимальную сумму весов рёбер, и без циклов.
На рисунке 6 показан процесс получения минимального остовного дерева.
Алгоритмы поиска минимального остовного дерева:
Алгоритм Прима.
https://habr.com/ru/post/569444/
https://ru.wikipedia.org/wiki/Алгоритм_Краскала
Алгоритм Крускала.
https://habr.com/ru/post/569444/
https://ru.wikipedia.org/wiki/Алгоритм_Краскала#:
:text=Алгоритм%20Краскала%20—%20эффективный%20алгоритм%20построения,некоторых%20приближений%20для%20задачи%20Штейнера.
Применяются:
для создания деревьев для распределения данных в компьютерных сетях;
в кластерном анализе с использованием графов;
при сегментации изображений;
при социально-географическом районировании, когда смежные регионы объединяются.
|
|
|
 Скачать 1.16 Mb.
Скачать 1.16 Mb.


