КИП книга каз. 1 блім физикалы шамаларды лшеуді техника негіздері

• Название: 1 блім физикалы шамаларды лшеуді техника негіздері
• Анкор: КИП книга каз.doc
• Дата: 24.04.2017
• Размер: 6.26 Mb.
• Имя файла: КИП книга каз.doc
• Тип: Документы; #4370
• страница: 2 из 11

1.4 Қателіктердің жіктелуі
Өлшеу процедурасы келесі кезеңдерден тұрады: өлшеу объектісінің үлгісін таңдау, өлшеу тәсілін таңдау, ӨЖ таңдау, нәтиже алу үшін тәжірибе жүргізу. Бұл өлшеу нәтижесі өлшенетін шаманың нақты мәні өлшеу қателігі деп аталатын қандай да бір шамаға өзгеретініне әкеп соғады. Өлшенетін шама анықталып, оның нақты мәннен ауытқуы мүмкін дәрежесі анықталған болса өлшеу аяқталды деп есептеуге болады.

Қателіктің пайда болу себептері өте коп, сондықтан олардың жіктелуі шартты сипатқа ие.

ӨЖ қателігі мен осы ӨЖ-мен өлшеу нәтижесінің қателігін ажырата білу керек. Өлшеу қателігі қолданылатын ӨЖ-нің метрологиялық сипатына, алынған өлшеу тәсіліне, сыртқы жағдайларға, сондай-ақ өлшенетін шама мен объект қасиеттеріне тәуелді. Өлшеу қателігі қолданылатын ӨЖ қателігінен әдетте жоғары болады, бірақ қателіктерді болдырмау тәсілдерімен және көпреттік бақылау деректерін статистикалық өңдеу арқылы кейбір жағдайларда өлшеу қателігін қолданылатын ӨЖ қателігінен азайтып алуға болады.

Өрнектелу тәсілі бойынша қателіктер абсолюттік, салыстырмалы және келтірілген болып жіктеледі.

Абсолюттік қателік — өлшенетін физикалық шама бірлігімен өрнектелетін ӨЖ қателігі:

Δ = Х_изм – Х_д . (1.3)

Салыстырмалы қателік — өлшеу құралының абсолюттік қателігінің өлшеу нәтижесіне немесе өлшенген физикалық шаманың нақты мәніне қатынасымен өрнектелетін ӨЖ қателігі:

γ_отн = (Δ/Х_д)100. (1.4)
Өлшеу құралы үшін γ_отн шкаланың берілген нүктесіндегі қателікті сипаттайды, ол өлшенетін шама мәніне тәуелді және құрал шкаласының ең кіші мәніне ие.

Көптеген өлшеу құралдарының сипаттамасы үшін келтірілген қателік қолданылады.

Келтірілген қателік - ӨЖ абсолюттік қателігінің барлық өлшеу диапазонында тұрақты шамасының шартты алынған мәніне қатынасымен өрнектелетін салыстырмалы қателік:
γ_прив = (Δ/Х_норм)100, (1.5)
мұндағы Х_норм — мөлшерлейтiн мән, яғни қателік есептелетін қатынас бойынша анықталатын орнатылған мән.

Мөлшерленетiн мәнді таңдау ГОСТ 8.009—84 стандартқа сәйкес жүргізіледі. Бұларға ӨЖ жоғарғы өлшеу шегі, өлшеу диапазоны, шкала ұзындығы, т.б. жатады. Келтірілген қателік бойынша көптеген өлшеу құралдарына дәлдік класы орнатылады.

Өлшеу құралының қателігі пайда болу себебі мен шарттарына байланысты негізгі және қосымша болып бөлінеді.

Негізгі қателік — қалыпты жұмыс шарттарындағы ӨЖ қателігі. Ол ӨЖ қасиеттерінің нашар болғандығынан пайда болады және ӨЖ-нің нақты функциясының номиналдыдан қалыпты жағдайлардағы айырмасын көрсетеді.

Нақты түрдегі ӨЖ-не нормативтік құжаттармен қалыпты өлшеу шарттары қойылады - бұл аздық салдарынан өлшеу нәтижелері өзгергенде ықпал етуші шамалар мәнінің жиынтығымен сипатталатын өлшеу шарттары. Мұндай ықпал етуші шамалардың арасында жиі тарағаны – қоршаған орта температурасы мен ылғалдылығы, кернеу, жиілік және қорек көзі қисығының пішіні, сыртқы электр және магнит өрістерінің болуы, т.б. қалыпты жағдайлар үшін нормативтік құжаттамамен ӨЖ қолдану қарастырылады:

Ықпал етуші шаманың қалыпты мәндер облысы (мәндер диапазоны): қоршаған орта диапазоны — (20 ± 5) ⁰С; құралдың орналасуы — ± 2° көлденеңінен ауытқыған көлденең; салыстырмалы ылғалдылық — (65 ± 15) %; электр және магнит өрістерінің болмауы, кернеу көзі — (220±4,4) В, қорек көзі жиілігі — (50± 1) Гц и т.д.;

Ықпал етуші шаманың жұмыс мәндер облысы - өлшеу құралының көрсеткіші өзгеретін немесе қосымша қателік қалыптандырылатын ықпал етуші шама мәндерінің облысы;

өлшеудің жұмыс шарттары – ықпал етуші шаманың мәндері жұмыс облысында орналасатын өлшеу шарты. Мысалы, өлшеу конденсаторы үшін қоршаған орта температурасының қалыптыдан ауытқуына қосымша қателікті мөлшерлейді; амперметр үшін – айнымалы токтың 50Гц-тен ауытқуынан болған көрсеткіш өзгерісі (значение частоты 50 Гц жиілік мәні бұл жағдайда қалыпты жиілік мәні болып есептеледі).

Қосымша қателік – қандай да бір ықпал етуші шамалардың ауытқуы салдарынан немесе олардың қалыпты мәндер облысынан ауытқуы салдарынан негізгі қателікке қосымша пайда болатын ӨЖ қателігінің құраушысы. Берілген өлшеу құралы үшін ең үлкен мән болып қарастырылатын негізгі және қосымша мәндер мөлшерленеді.

Жіберілетін негізгі қателік шегі - ӨЖ жарамды деп есептеліп, техникалық жағдайларда қолдануға жіберілетін ең үлкен негізгі қателік.

Жіберілетін қосымша қателік шегі - өлшеу құралы қолдануға жіберіле алатын ең үлкен қосымша қателік. Мысалы, 1,0 дәлдік класындағы құрал үшін температура 10⁰С-ге өзгергенде келтірілген қосымша қателік ±1 %-дан аспауы қажет. Яғни, орта температурасы әр 10⁰С-ге өзгерген сайын қосымша қателік 1 %-ға арта түседі.

Жіберілетін негізгі және қосымша қателіктер шегі абсолют, салыстырмалы және келтірілген қателіктер түрінде өрнектеледі.

Жіберілетін негізгі және қосымша қателіктер шегімен анықталатын, дәлдік дәрежесін бейнелейтін және дәлдікке әсер ететін мінездемелермен де анықталатын өлшеу құралдарының жалпыланған мінездемесі ӨЖ дәлдік класы деп аталады. Дәлдік класы бір типті ӨЖ-нің қателігі қандай шекте жатқанын, бірақ осы құралдардың әрбірінің көмегімен орындалатын өлшеу дәлдігінің тікелей көрсеткіші болмайтынын көрсетеді, өйткені қателік өлшеу тәсіліне де, өлшеу шарттарына да тәуелді. Бұл берілген өлшеу дәлдігіне байланысты ӨЖ таңдауда ескеріледі. Нақты ӨЖ дәлдік класы стандартты техникалық талаптарда немесе басқа нормативтік құжатамаларда орнатылады. Мысалы, 0,5 класты құрал 0,5 %-дан аспайтын негізгі қателікке ие болады. Сонымен бірге құрал жіберілетін қосымша қателікке қатысты сәйкес талаптарды да қанағаттандыруы қажет. Мысалы, ГОСТ 8.401—80 аналогтық электромеханикалық құралдар үшін: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0; 6,0 сияқты тоғыз дәлдік класын орнатады.

ӨЖ дәлдік класын біле отырып, (1.5)-тен барлық диапазон нүктелері үшін ең үлкен жіберілетін абсолют қателік мәнін табуға болады:

Δ_{max доп}=γ_прив·Х_норм /100. (1.6)
Қателіктің өзгеру сипатына қарай жүйелік, кездейсоқ және мүлт кетулер (промахи) болып бөлінеді.

Жүйелi қателiк — өлшеу құралының тұрақты немесе заңды өзгермелі деп алынатын қателік құраушысы. Берілген ӨЖ жүйелік қателігі осы типтегі басқа ӨЖ-нің жүйелік қателігінен айырмашылығы болады, нәтижесінде біртипті ӨЖ топтары үшін жүйелік қателік кейде кездейсоқ қателік ретінде қарастырылуы мүмкін.

Жүйелік қателіктерге әдістемелік, құралдық, субъективтік және өлшеу кезінде міндетті түрде ескерілетін және болдырмауды қажет ететін басқа да қателіктер жатады.

Кездейсоқ қателік – кездейсоқ өзгеретін қателік құраушысы. Ол көрсеткіштердің бірмәнсіздігіне әкеп соғады және алдын-ала болжанбайтын және ескерілмейтін себептермен шартталған. Алайда бірнеше қайталанған тәжірибе жүргізгенде ықтималдық теориясы мен математикалық статистика өлшеу нәтижесін анықтауға мүмкіндік берді, яғни бір реттік өлшемге қарағанда нақты мәнге жақын мәнді табуға мүмкіндік берді.

Мүлт кетулер (промахи) — оператор қателігіне немесе ескерілмеген сыртқы әсерлермен байланысты дөрекі қателіктер. Оларды әдетте өлшеу нәтижелерінен шығарып тастайды.

Өлшенетін шама мәніне байланысты қателіктер аддитивтік, кіріс шама Х мәніне тәуелсіз және мультипликативті-Х-пропорционалды болып бөлінеді.

Аддитивтік қателікΔ_адд, құрал сезгіштігіне тәуелді емес және барлық өлшеу диапазонында Х кіріс шаманың барлық мәндерінде тұрақты болып табылады (1.4, а-сурет). Бұл қателік көздері: тіреулердегі үйкеліс, шулар, сілтеулер, вибрация. Құралдың аддитивтік қателігіне мысал ретінде сандық құралдардағы нөл қателігін, дискреттік қателікті келтіруге болады. Осы қателік мәнінен кіріс шаманың ең кіші мәні тәуелді. Егер құралға аддитивтік қателік тән немесе ол басқа құраушылардан әлдеқайда көп болса, онда жіберілетін негізгі қателіктің шегі келтірілген қателік түрінде мөлшерленеді (1.5).

Мультипликативтік қателік құрал сезгіштігіне тәуелді және кіріс шаманың ағымдағы мәніне пропорционал өзгереді (1.4, б-сурет). Бұл қателік көзі: ӨЖ-нің жеке элементтерінің реттеу қателіктері(мысалы, шунттың немесе қосымша резистордың), элементтердің ескіруі, олардың мінездемелерінің өзгеруі, сыртқы факторлар әсері.

Егер құралға тек мультипликативтік қателік тән болса және ол өте үлкен болса, онда жіберілетін салыстырмалы қателік мәні салыстырмалы қателік түрінде өрнектеледі (1.4). мұндай ӨЖ дәлдік класы дөңгелекке орналасқан және жіберілетін салыстырмалы қателік шегіне тең бір санмен белгіленеді.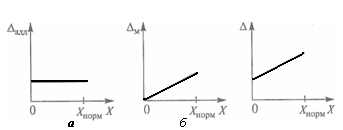

1.4-сурет өлшеу құралдары мен түрлендіргіштер қателігінің графигі:

а — аддитивтік; 6 — мультипликативтік; в — қосынды
қосынды абсолюттік қателік (1.4, в-сурет) мына формуламен анықталады:
            Δ=Δ_адд+Δ_м=γ_аддХ_норм+γ_мХ,(1.7)
мұндағы γ_адд = Δ_адд/Х_норм - аддитивтік қателіктің келтірілген мәні; γ_м= Δ_м/X — мультипликативтік қателіктің салыстырмалы мәні.

Сонда қосынды сплыстырмалы қателік былай анықталады:
(1.8)
Мұндағы d=γ_адд ;c = γ_адд +γ_м .

Аддитивтік және мультипликативтік құраушылары мөлшерлес өлшеу құралдары үшін жіберілетін салыстырмалы қателік шегі екімүшелік формуламен (1.8) өрнектеледі. Олар үшін дәлдік класы пайыздық c және d және қисық сызықпен бөлінген (c/d) түрде өрнектелген екі санмен белгіленеді, мысалы 0,02/0,01 класы. Мұндай белгілеу ыңғайлы, себебі Х=Х_норм кезінде оның бірінші мүшесі с салыстырмалы қателікке тең. Второй член формулы (1.8) формуласының екінші мүшесі Х-тің мәні, яғни аддитивтік қателік құраушысы азайғанда салыстырмалы қателіктің ұлғайғанын көрсетеді. Бұл топқа сандық көпірлер, қолмен жүргізілетін және автоматты теңдестіруі бар компенсаторлар жатады.

Аддитивтік және мультипликативтік қателіктердің жүйелік және кездейсоқ құраушылары болады.

ӨЖ қателігі сондай-ақ шкала ұзындығына да мөлшерленеді. Бұл жағдайда дәлдік класы (1.5) бұрышта орналасқан екі сызық арасындағы пайыздық бір санмен белгіленеді. Оларға бірқалыпсыз шкалалы құралдар (мысалы, гиперболалық немесе логарифмдік) құралдар жатады. Нақты дәлдік кластар қатары ӨЖ-нің әр түріне стандартпен орнатылады.

Өлшенетін шаманың өзгері сипатына қарай қателіктер статикалық және динамикалық болып бөлінеді.

Статикалық қателік — өзгермейтін есебінде алынған физикалық шаманы өлшеуге қажет қателік.

Динамикалық қателік— ӨЖ-нің инерциялық қасиеттерінің нәтижесінен болатын өзгермелі физикалық шаманы өлшеу қателігі.
1.5 Жүйелік қателіктер
Жүйелік қателіктердің пайда болуы белгілі әдістеме жетіспеушіліктерінің, тәжірибешінің қателіктерінің, өлшенетін шаманың барлық ерекшеліктерінің толық ескерілмегендігінің салдары болып табылады. Сондықтан жүйелік қателіктерді табу көбінесе тәжірибешінің өлшеу жүргізудің нақты шарттары мен әдістерін қаншалықты терең меңгергеніне байланысты.

өзгеру сипаты бойынша жүйелік қателіктер тұрақты (шамасы мен белгісін сақтайтын) және айнымалы (белгілі заң бойынша өзгеретін) болып бөлінеді.

Тұрақты жүйелік қателіктер — бұл аналогтық құралдар шкаласының бөлiктену қателiктерi; шунттардың мерзімді қиыстыруының дәл еместігімен, қосымша кедергiлермен, элемент параметрлерiнiң температуралық өзгерiстерiмен тағы басқаларымен шартталған қателіктер.

Айнымалы жүйелік қателіктер – бұл сыртқы магнит өрісі және басқа сыртқы шамалардың әсерінен кернеу көзінің тұрақсыздығымен шартталған қателіктер.

Пайда болу себептеріне қарай әдістемелік, аспаптық және субъективтік болып бөлінеді.

Әдістемелік қателіктер алынған өлшеу тәсілдерінің теориялық негіздерінің толық еместігі, қарапайым болжамдарды қолданудың, өлшенетін шаманы дұрыс таңдамаудың нәтижесінде болады. Мысалы, температураны термопар көмегімен өлшеу кезінде зерттелетін объекттің температуралық режимінің бұзылуынан болатын қателік кездеседі.

Әдістемелік қателіктер көзін анықтау мен оларды болдырмау – тәжірибе техникасында ең бастысы. Осы мәселені шешу деңгейі метрологиялық дайындықпен және тәжірибеші шеберлігімен шешіледі. Көп жағдайларда әдістемелік қателіктер жүйелік, кей жағдайларда кездейсоқ сипатқа ие, мысалы, жұмысшы теңдей коэффициенттері кездейсоқ өзгеретін өлшеу шартына тәуелді болған кезде.

Аспаптық қателіктер (өлшеу қателігінің құраушылары) қолданылатын ӨЖ қасиеттерімен (сыртқы әсерлерге тұрақтылықпен, сезімталдықпен), олардың өлшеу объектісіне әсерімен, дайындау технологиясымен және сапасымен (мысалы, бөліктеу дәлсіздігі, жұмыс кезінде құралдың мінездемелерінің өзгеруі, т.б.) шартталады. Бұл қателік өз кезегінде негізгі және қосымша болып бөлінеді.

Субъективтік қателіктер өлшеу жүргізетін оператордың күйімен, оның жұмыс уақыты кезіндегі жағдайымен, сезім мүшелерінің күйімен, өлшеу құралдарының эргономикалық қасиеттерімен байланысты – бұның барлығы белгi соғу дәлдiгінен білiнедi. Субъек­тивтік қателіктер кей жағдайларда кездейсоқтар разрядына өтуі мүмкін. Сандық құралдары мен автоматты өлшеу әдістерін қолдану мұндай қателіктерді болдырмауға мүмкіндік береді.

Жүйелік қателіктерді тауып, оларды болдырмау үшін жүйелік қателіктердің пайда болу себептерін алдын ала болдырмау (түзетілген және сенімді өлше құралдарын қолдану, тәжірибе шарттарын сақтау, өлшеу тәсілін таңдау негіздері), сондай-ақ белгісі бойынша қателікті орынбасу және компенсациялау жүзеге асырылады.

•  орынбасу тәсілі өлшенетін шаманың реттелетін өлшем көмегімен алынған белгілі шамамен ауыстырылатынына негізделген. Егер мұндай орынбасу жұмыс құралында еш өзгеріссіз орындалса және орынбасқаннан кейін дәл сол көрсеткіштер байқалса, онда өлшенетін шама реттелетін өлшеммен есептелген белгілі шамамен ауыстырылады. Бұл тәсіл тұрақты жүйелік қателіктерді болдырмайды. Орынбасу тәсілін қолданғанда өлшеу қателігі өлшем қателігімен және белгісізді ауыстыратын шама мәнін есептегенде пайда болатын қателікпен анықталады.

• компенсациялау тәсілі өлшеу шартына байланысты жүйеліктердің бір белгімен өлшеу нәтижесіне кіре алатын жүйелік қателігін болдырмайды (термоЭҚК-нен қателік, тұрақты электр және магнит өрісі кернеулігі әсерінен қателік). Бұл жағдайда тәжірибе екі рет жүргізіледі, бір рет қателік нәтижеге бір таңбамен, екіншісінде – кері таңбамен енгізілуі қажет. Екі алынған нәтиженің орташа мәні жоғарыда көрсетілген жүйелік қателіктерден бөлек өлшеулердің соңғы нәтижесі болып табылады.

Функционалдық тәуелділік себебі мен түрін анықтау өлшеу нәтижесіне сәйкес түзетулер енгізу арқылы жүйелік қателікті өтеуге болады. Жүйелік қателікті болдырмау мақсатымен өлшеу кезінде алынған шамаға қосылуы қажет өлшенетінмен аттас шама мәнін түзету деп атайды. Кейбір жағдайда осы мақсатпен өлшеу нәтижесі көбейтілетін сан – түзетуші көбейткіш қолданылады.

Түзету немесе түзетуші көбейткіш ӨЖ тексеру, сәйкес кестелер мен графиктерді қолдану көмегімен анықталады. Сондай-ақ түзетуші мәндерді табудың есептік тәсілдері де қолданылады.

Автоматтық өлшеулер жүргізгенде жүйелік қателіктерді схемалық түзету әдістері қолданылады, мысалы, түрлендіргіштердің компенсациялық қосылуы, түрлі температуралық және жиіліктік түзету тізбектері және т.б.

Өлшеу техникасына микропроцессорлық жүйесі бар құралдарды ендіру нәтижесінде жаңа мүмкіндіктер пайда болды. Олардың көмегімен жүйелік қателіктердің көптеген түрін, әсіресе аспаптық қателіктерді түзетуге немесе істен шығарып тастауға болады. Бөліктеудің дәлсіздігімен байланысты автоматты түзету енгізу, қосымша қателіктерді есептеу және істен шығару, нолді ығыстырумен байланысты қателіктерді болдырмау – осы және басқа да түзетулер өлшеу дәлдігін арттырады.
1.6 Кездейсоқ қателіктер
Кездейсоқ және жүйелік қателік құраушыларының табиғаты мен физикалық мәні әртүрлі. Алайда барлық жағдайларда жүйелік те, кездейсоқ та қателіктерді бағалау кезінде белгілі статистикалық ережелер негізінде өлшеу нәтижелерінің жиынтығы түріндегі статистикалық материал өңделеді. Жалпы жағдайда осы қателіктерді кездейсоқ шама ретінде қарастырамыз. Оларда «кездейсоқтық» табиғаты әртүрлі. Өлшеу нәтижесіндегі кездейсоқ қателіктер көптеген себептерге, мысалы жұмыс істеп тұрған құралдағы физикалық процестер (үйкеліс, шу) немесе өлшеу шарттарының кездейсоқ өзгеруінен болады. Жүйелік қателіктер бағасының «кездейсоқтығы» - білместік немесе олардың шынайы мәндерін нақты анықтамағандықтың нәтижесі. Алайда кездейсоқ қателіктердің соңғы өлшеу нәтижесіне әсерін өлшеу санын көбейту арқылы азайтуға болады. Төменде келтірілген кездейсоқ шамалардың ықтимал-статистикалық үлгілері кездейсоқпен бірге қосынды қателіктер үшін де жарайды.

Ықтималдық теориясының математикалық аппаратын қолданатын қателіктер теориясы бірнеше қайталанған өлшеулер нәтижесі мен кездейсоқ жағдайлар арасындағы ұқсастыққа негізделген.

Ықтималдық теорясынан белгілі, кездейсоқ шамаларды суреттеу үшін оны тарату заңдары қолданылады.

Кездейсоқ шаманы тарату заңы кездейсоқ шаманың мүмкін мәндері Х мен оларға сәйкес ықтималдықтар арасындағы қатынасты орнатады. Тарату заңы кесте, формула, график түрінде берілуі мүмкін. Ол кездейсоқ шаманың қасиеттері туралы ақпарат береді, оның мәнін бағалауға және берілген шектерде оның мәндерін табу ықтималдығын анықтауға мүмкіндік береді.

Дискретті және үзіліссіз (1.5, а-сурет) кездейсоқ шамалар үшін тәжірибеде көбінесе интегралдық тарату функциясы F(x) түріндегі тарату заңы қолданылады. Бұл функция Х_i кездейсоқ шамасының i –ші тәжірибеде х шамасынан кіші мәнге ие болатын ықтималдықпен анықталады:
F(x)=P(X¡
Интегралдық тарату функциясы келесі қасиеттерге ие — ол теріс емес, яғни т.е. F(x) > 0; төмендемейді, яғни F(x₂) > > F(x_l), егер x₂>х₁; 0-ден 1-ге дейін өзгереді, яғни F(-∞) = 0, F(+∞) = 1. тарату заңының әмбебаптығы мен тәжірибелік қолданысын түсіндіретін маңызды қасиетіне х1-ден хө2-ге дейінгі аралықта кездейсоқ шаманы табу ықтималдығы тарату функциясының айырымына тең болуы жатады, яғни
P(x₁≤X₂) = F(x₂)-F(x₁). (1.9)
Үздіксіз кездейсоқ шамалардың таралуын суреттеу үшін тарату тығыздығы деп аталатын F¹(х) тарату функциясының бірінші туындысы қолданылады. Бұл р(х) =(x) = dF(x)/dx тарату функциясының бірінші туындысын тарату функциясының өзін анықтағанға қарағанда өте оңай екенімен байланысты.

Р(х) ықтималдық тығыздығы (дифференциал тарату функциясы) х до х + dx шексіз аз аралықта Х кездейсоқ шамасы dx→0 болғанда dx аралығындағы шама мәнін алу ықтималдығының қатынас шегі ретінде анықталады:
(1.10)
Тарату функциясы ықтималдық тығыздығымен өрнектеледі:



Кездейсоқ шаманың берілген аралыққа түсу ықтималдығы (Х₁, Х₂) төмендегідей: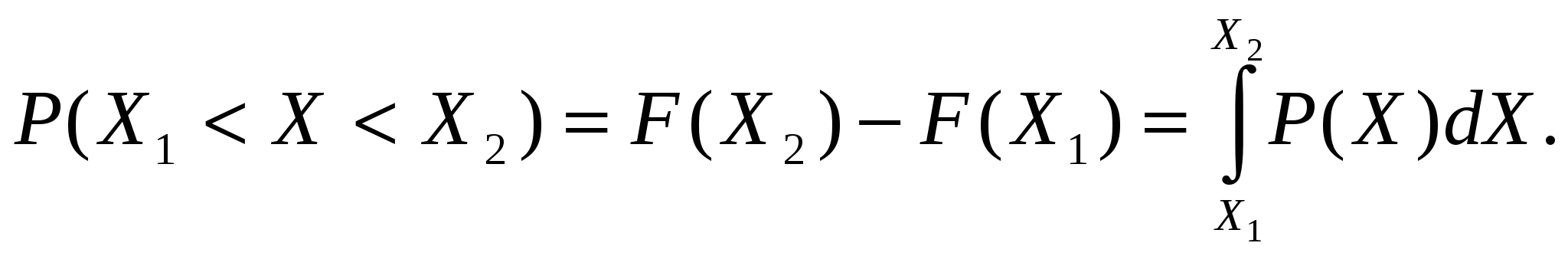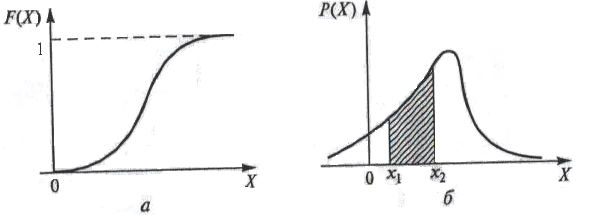





1.5-сурет үздіксіз кездейсоқ шаманың таралу заңы:

а — интегралдық; 6 — дифференциал
Графиктік түрде бұл ықтималдық таралу қисығымен шектелген қисықсызықты трапецияның ауданына тең, абсцисса осімен және түзулермен Х = x₁ және Х = х₂ (1.5, б-сурет).

Кездейсоқ шаманы таралу заңымен статистикалық суреттеу өте қиын. Тәжірибеде осы таралу заңының белгілі қасиеттерін сипаттайтын кездейсоқ шаманың сандық таралу заңымен шектеледі. Сандық мінездемелер арасында математикалық күтім, мода және медиана кездейсоқ шаманың сандық осьтегі мінездемесі болып табылады.

Кездейсоқ шаманың математикалық күтімі(оның орташа мәні) дискреттік кездесоқ шаманың Х осы мәндердің ықтималдығына Р барлық мүмкін мәндерінің тундысының қосындысы ретінде анықталады:

                                                  (1.11)
Үздіксіз кездейсоқ шама үшін математикалық күтім

    (1.12)
мұндағы Р(Х) — Х кездейсоқ шама ықтималдығының таралу тығыздығы.

Мода М₀[Х] — дискреттік шамада ең үлкен ықтималдыққа, ал үздіксіз шамада – ең үлкен ықтималдық тығызыдығына ие болатын Х кездейсоқ шама мәні. Бір максимумы бар таралу қисығы бірмодалық (1.5, б-сурет), екі максимумы бар-екімодалық, бірнеше бірдей максимумы бар – көпмодалық деп атайды.

Х кездейсоқ шаманыңМедианасы М_е[Х] кездейсоқ шама кіші не үлкен болатындай бірдей ықтимал мәнін сипаттайды. Симметриялық модалық таралу жағдайында медиана математикалық күтіммен және модамен сәйкеседі.

Кездейсоқ шаманың таралу сипатына дисперсия және орташа квадраттық ауытқу жатады.

Х кездейсоқ шаманың Дисперсиясы— кездейсоқ шаманың математикалық күтімнен ауытқу квадратының математикалық күтімі. Дискреттік кездейсоқ шама үшін дис­персия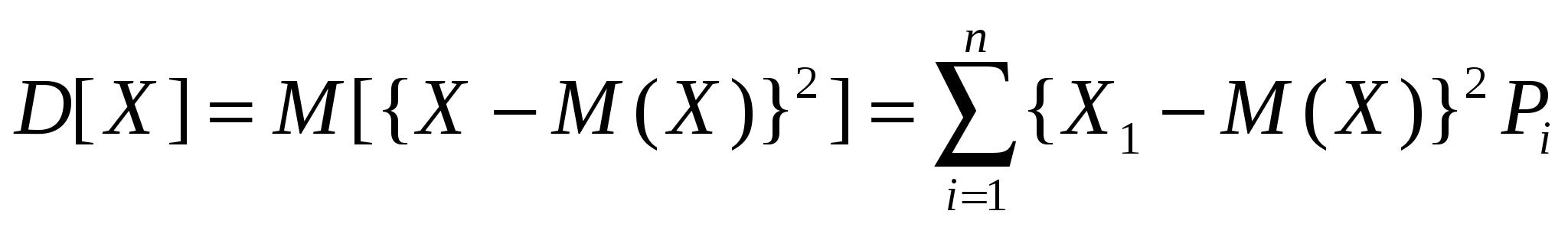

, (1.13)

Үздіксіз кездейсоқ шама үшін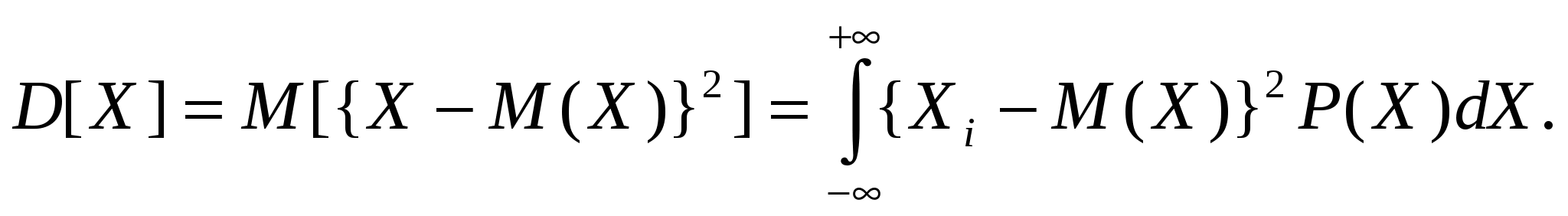
                      (1.14)

Кездейсоқ шаманың орташа квадраттық ауытқуы — дисперсиядан квадраттық түбір:

                                                                                                              (1.15)

Кездейсоқ шамалардың қарастырылған күй және таралу сипаттарынан басқа таралудың белгілі бір қасиетін сипаттайтын ықтималдық мінездемелер де қолданылады. Мұндай сипаттамаларға бастапқы және орталық моменттер жатады. X кездейсоқ шаманың математикалық күтімі бастапқы момент М[Х] = α₁, ал дисперсия — екінші орталық момент D[X] = μ₂. Үшінші орталық момент μ₃ математикалық күтімге қатысты таралу қисығының асимметрия дәрежесін сипаттайды. Ыңғайлы болу үшін асимметрия сипаты ретінде асимметрия коэффициенті деп аталатын өлшемсіз шама алынады

Бірмодалық таралуда асимметрия оң (A_s> 0), егер М₀[Х] модасы М[Х] орташа мәннің сол жағында болса, және ол теріс (А_s< 0), егер М₀[Х] модасы М[Х] орташа мәннің оң жағында болса (1.6-сурет). Симметриялық таралуда A_s= 0 (1.7, а-сурет).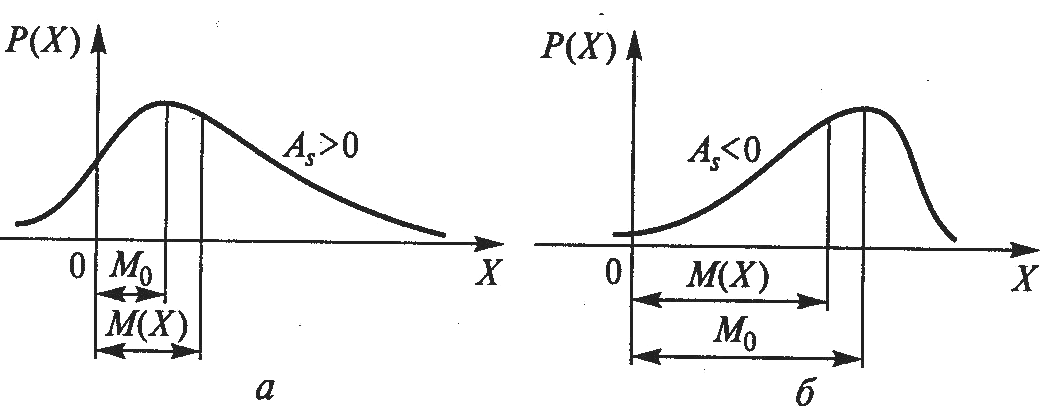



1.6-сурет. Оң (а)және теріс (б) асимметрия коэффициенттері бар ықтималдық тығыздының қисығы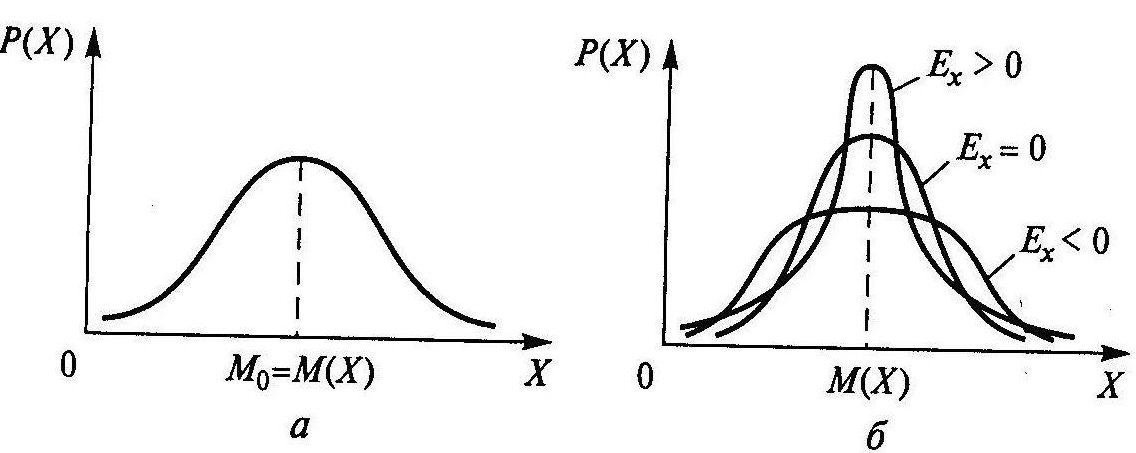


1.7-суреттүрлі эксцесса коэффициенттері бар ықтималдық тығыздығының қисықтары
Төртінші орталық момент μ₄ таралу қисығының үшкіртөбелігін немесе жазықтөбелігін сандық сипаттайды және эксцес деп аталатын өлшемсіз шамамен Е_х анықталады:

Симметриялық бірмодалық таралуда эксцесс оң (Е_x > 0), егер таралу қисығы үшкіртөбелі болса, және теріс (Е_х < 0), егер таралу қисығы жазықтөбелі болса. Қалыпты таралуда эксцесс нолге тең (Е_x = 0) (1.7, б-сурет).

Осы үш моментті қолданып таралу заңының теориялық үлгісін құруға болады.

Метрологиялық тәжірибеде жиі қолданылатын теориялық заңдардың бірі – симметриялық және ықтималдық тығыздықтың монотондық кему қасиеттеріне ие өлшеу қателігінің теориялық таралу заңы:

• абсолюттік мәні бойынша тең, бірақ белгісі бойынша қарама-қарсы

•  қателіктер жиі бірдей кездеседі (сим­метрия аксиомасы);

•  кіші қателіктер үлкенге қарағанда жиі кездеседі; өте үлкен қателіктер кездеспейді.

М(Δ) = 0 кезінде орталықтанған кездейсоқ шаманың қалыпты таралуы бірмодалық болып табылады және төмендегідей өрнектеледі
                 (1.16)
Қалыпты таралу заңы үшін Х1 және Х2 мәндерінің арасындағы қателіктерді табу ықтималдығы таралу функциясының сәйкес мәндерінің айырымымен анықталады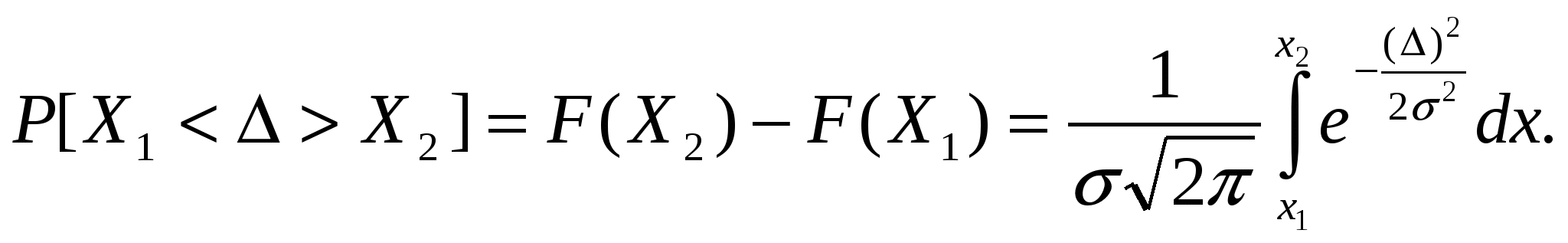

       (1.17)
Бұл ықтималдық графиктік түрде Х₁ және Х₂ абсциссаларына сәйкес ординаталар арасындағы ықтималдық тығыздығын бейнелейтін қисық ауданы түрінде көрсетілген.

σ –нің түрлі мәндеріндегі қалыпты қателік таралуының тығызыдық графигі (1.16) 1.8-суретте көрсетілген.1.8-суреттен көрініп тұрғандай σ кіші болған сайын қисық Δ осіне қаттырақ енеді және солмен үшкіртөбелене түседі (σ₁ < σ₂ <σ₃).

Қалыпты заң өлшеу қателігі әрқайсысы ортақ қателікке басқаларымен бірдей үлесін қосатын үлкен көлемді кездейсоқ факторлармен шартталған кезде жүзеге асады. Осы кезде қателік құраушысының таралу заңы түрлі болады (бірқалыпты, үшбұрышты, трапециялық, экспоненциал, т.б.)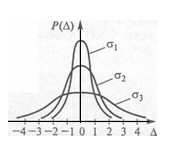


1.8-сурет σ-нің түрлі мәндеріндегі қателіктің қалыпты таралу тығыздығының графигі
Егер x₁ = -∞, а х₂ = + ∞ болса, онда (1.17)-мен анықталатын ықтималдық қисық астындағы ауданға сәйкес келетін бірлікке ұмтылады (1.5-суретті қара).

Тәжірибеде есептеулер жүргізу үшін қалыптандырылған Лаплас функциясы қолданылады, оны басқаша ықтималдық интегралы деп те атайды.
  (1.18)
мұнда t=x/σ.

Сонда (Х₁, Х₂) берілген шектерде қателікті табудың есептік ықтималдығы Лаплас функциясы аргументтерінің кестелік мәндері арқылы табылады:
(1.19)

мұнда t₁ = x₁/σ; t₂ =х₂ /σ.

(1.19) формуласы өлшеу нәтижесі белгілі ықтималдықпен жататын интервал шегін (сенімді интервал) есептеуге мүмкіндік береді (1.9-сурет).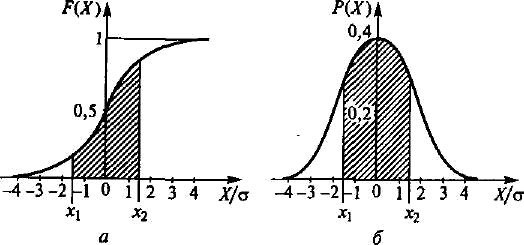


1.9-сурет қалыптандырылған таралу функциясы: а — интегралдық; б — дифференциалдық
Өлшеу құралдары мен қолданылатын әдістер сипатын есептеу жолымен бағаланатын немесе өлшеу нәтижелері бойынша бағаланатын негізгі нүктелік сипаттамаларға математикалық күтім, дисперсия және орташа квадраттық ауытқу жатады. Кездейсоқ шаманың математикалық күтімін (МК) бағалау өлшенетін шаманың орташа арифметикалық мәні (ОАМ) есептеледі
                                            (1.20)
Нүктелік дисперсия құны

                                                                                    (1.21)
Орташа арифметикалық мәндердің нәтижесін абсолюттік бірлікте таралу сипатын алу үшін орташа квадраттық ауытқу қолданылады
                                  .                                  (1.22)

Алынған бағалар — математикалық күтім мен орташа квадраттық ауытқу кездейсоқ шама болып табылады, сондықтан орташа квадраттық ауытқу 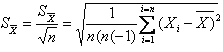шашылуды бағалау үшін қолданылады:
                              ,                         (1.23)
ал σ[Х] ОКА - σ[Х] шашылуын бағалау үшін:
                                                           (1.24)
Мұнда Е_х— эксцестің сандық мәні.

Сандық түрде таралу параметрлерін сипаттайтын нүктелік бағалар әдетте үлкен көлемде қолданылады. Нақты көлемдер кiшiрейген сайын олардың ақиқаттығының дәрежесi азаяды, сондықтан берілген ықтималдықпен бағаланатын параметрдің шынайы мәні орналасатын аралықты анықтауға мүмкіндік беретін интервалдық бағалауға көшеді.

Вероятность того, что действительное значение измеряемой ве­личины X өлшенетін шаманың нақты мәні осы сенімді интервалда (-х₂, +х₁) болу ықтималдығы берілген дәлдіктегі сенімділікβ деп аталады.

Өлшеу практикасында сенімді ықтималдықтың түрлі мәндері бар, мысалы: 0,90; 0,95; 0,98; 0,99; 0,9973 и 0,999. сенімді аралық пен сенімді ықтималдық нақты өлшеу шарттарына байланысты таңдалады. Сонымен, мысалы, например, при нормальном законе распределения случайных по­грешностей со среднеквадратичным отклонением σ орташа квадраттық ауытқуы бар кездейсоқ қателіктің қалыпты таралу заңы кезінде көбінесе +3σ-тен -3σ-ке дейінгі сенімді аралық қолданылады, ол мұнда сенімді ықтималдық 0,9973-ке тең. Мұндай сенімді ықтималдық орта алғанда 370 кездейсоқ қателіктердің тек біреуі ғана абсолюттік мәні бойынша 3σ-тен үлкен болвтынын көрсетеді. Жеке өлшемдер саны тәжірибеде әдетте бірнеше ондағаннан асатындықтан 3σ-тен үлкен кездейсоқ қателіктің біреуінің болуы сирек кездесетін жағдай. Бұл қалыпты заңмен таралған барлық мүмкін кездейсоқ қателіктер абсолюттік мәні бойынша 3σ-тен аспайтынын жеткілікті негізбен айтуға болатынын көрсетеді («үш сигма» ережесі). Қателік 3σ мәнінен шығып кеткен жағдайда оны «мүлткету» деп есептеуге болады. «мүлткетуді» анықтау үшін «үш сигма» - Смирнов, Райт, Романов­ский, Шовенэ және т.б. критериі қолданылады.