1. Частные виды матриц. Умножение матриц, свойства

• Название: 1. Частные виды матриц. Умножение матриц, свойства
• Дата: 31.03.2018
• Размер: 296.98 Kb.
• Имя файла: 2.docx
• Тип: Документы; #39954
• страница: 3 из 3

37.Канонические уравнения прямой в пространстве

Каноническими уравнениями прямой в пространстве называются уравнения, определяющие прямую, проходящую через заданную точку коллинеарно направляющему вектору.Пусть дана точка и направляющий вектор . Произвольная точка лежит на прямой l только в том случае, если векторы и коллинеарны, т. е. для них выполняется условие:

.

Приведённые выше уравнения и есть канонические уравнения прямой.

Числа m, n и p являются проекциями направляющего вектора на координатные оси. Так как вектор ненулевой, то все числа m, n и p не могут одновременно равняться нулю. Но одно или два из них могут оказаться равными нулю. В аналитической геометрии допускается, например, такая запись:

,

которая означает, что проекции вектора на оси Oy и Oz равны нулю. Поэтому и вектор , и прямая, заданная каноническими уравнениями, перпендикулярны осям Oy и Oz, т. е. плоскости yOz.

Уравнения прямой, проходящей через две данные точки

Прямая может быть задана двумя лежащими на ней точками и В этом случае направляющим вектором прямой может служить вектор . Тогда канонические уравнения прямой примут вид

.

Приведённые выше уравнения и определяют прямую, проходящую через две заданные точки.

Прямая как линия пересечения плоскостей

Прямая в пространстве может быть определена как линия пересечения двух непараллельных плоскостей и , т. е. как множество точек, удовлетворяющих системе двух линейных уравнений



Уравнения системы называются также общими уравнениями прямой в пространстве.

Параметрические уравнения прямой в пространстве

Если даны некоторая точка и направляющий вектор, то можно составить не только канонические, но и параметрические уравнения прямой в пространстве. Пусть даны и направляющий вектор .

Тогда



где t - параметр .

вопрос 38

Прямая и плоскость в пространство могут:

• 
  а) не иметь общих точек;
  
• 
  б) иметь ровно одну общую точку;
  
• 
  в) иметь хотя бы две общие точки.
  

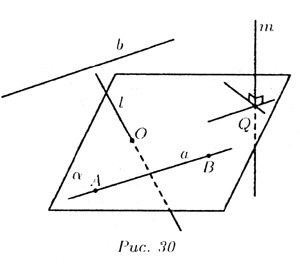38. Условие параллельности, перпендикулярности.

На рис. 30 изображены все эти возможности.

В случае а) прямая b параллельна плоскости: b || .

В случае б) прямая l пересекает плоскость в одной точке О; l = О.

В случае в) прямая а принадлежит плоскости : а или а .

Теорема. Если прямая b параллельна хотя бы одной прямой а, принадлежащей плоскости , то прямая параллельна плоскости .

Предположим, что прямая m пересекает плоскость в точке Q.Если m перпендикулярна каждой прямой плоскости , проходящей через точку Q, то прямая m называется перпендикулярной к плоскости .

Трамвайные рельсы иллюстрируют принадлежность прямых плоскости земли. Линии электропередачи параллельны плоскости земли, а стволы деревьев могут служить примерами прямых, пересекающих поверхность земли, некоторые перпендикулярные плоскости земли, другие — не перпендикулярные (наклонные).

39) Расстояние от точки до прямой на плоскости и от точки до плоскости.

Расстояние d точки M0 (x0,y0) до прямой xcosα+ysinα-p=0 (нормальное уравнение прямой) вычисляется по формуле :

d=|x0cosα+y0sinα-p|

или, если прямая задана общим уравнением Ax+By+C=0 , то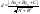

Расстояние от точки M0(x0,y0,z0) до плоскости, заданной общим уравнением Ax+By+Cz+D=0 , определяется по формуле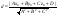


40) Взаимное расположение прямых на плоскости.

Если даны две прямые

A1x+B1y+C1=0 и A2x+B2y+C2=0

то их точка пересечения находиться совместным решением двух данных уравнений. Если уравнения несовместны, то прямые не имеют общей точки, т.е. параллельны.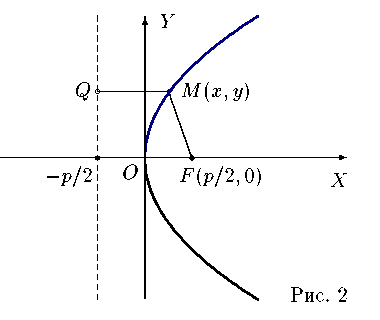

№41 Взаимное расположение плоскостей.

Две плоскости в пространстве либо параллельны, либо пересекаются по прямой.

Две плоскости называются параллельными, если они не имеют общих точек.

Признак параллельности плоскостей:Если две пересекающиеся прямые одной плоскости параллельны соответственно двум прямым другой плоскости, то эти плоскости параллельны.
Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
Через каждую точку пространства, не лежащую в данной плоскости, можно провести плоскость, параллельную этой плоскости, и притом только одну.
Плоскости пересекаются по прямой, все точки которой принадлежат обеим плоскостям.
Отдельным случаем является совпадение плоскостей, когда все точки одной плоскости , принадлежат другой плоскости.

№42 Взаимное расположение прямых в пространстве.
Две прямые в пространстве либо пересекаются, либо параллельны, либо скрещиваются.
Две прямые, которые не имеют общих точек и не параллельны, называются скрещивающимися.
Прямые, не имеющие общих точек, называют параллельными.
Через данную точку можно провести только одну прямую, параллельную данной.
Прямые, имеющие общую точку, называют пересекающимися.
Также возможен случай совпадения прямых, когда все точки одной прямой, принадлежат другой прямой

43)Взаимное расположение прямой и плоскости в пространстве.

Прямая относительно плоскости в пространстве может быть:

А) параллельна

B) пересекать плоскость

С) лежать в этой плоскости

Прямая параллельна плоскости, если скалярное произведение вектора нормали плоскости(N) и направляющего вектора прямой (S) равно нулю. Если при этом какая-либо точка прямой будет принадлежать и плоскости, то вся прямая будет принадлежать плоскости.

Прямая пересекает плоскость, если скалярное произведение вектора нормали плоскости(N) и направляющего вектора прямой (S) не равно нулю.

45.Эллипс. Определение, каноническое уравнение.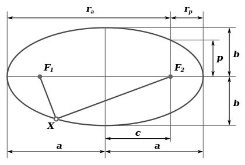

Эллипс – множество всех точек на плоскости сумма расстояний каждой и зкоторых от двух данных точек этой плоскости (Фокусы F1,F2) есть постоянная величина.

F1(-c;0), F2(c:0). Пусть Х – произвольная точка на эллипсе с координатами (х,у). Согласно определению можно записать:

|F1M|+|F2M|= 2a -> ->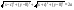

Каноническое уравнение: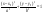



46.Гипербола и парабола. Определение, каноническое уравнение.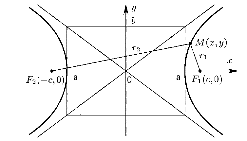

Гипербола – это геометрическое множество точек плоскости, абсолютное значение которых до двух данных точек (F1 и F2) есть величина постоянная, равная 2а

F1(-c;0), F2(c:0). Пусть М – произвольная точка на эллипсе с координатами (х,у). Согласно определению можно записать:

|F1M|-|F2M|= ±2a -> ->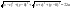

Каноническое уравнение: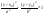



Парабола – это геометрическое место точек плоскости равноудаленных от данной точки (фокуса) и от данной прямой – директрисы.

Директриса определяется уравнением х=-p/2, фокус расположен в точке F(p/2;0). Записывая равенство расстояний между произвольной точкой кривой M(x;y) и фокусом и между точкой M(x;y) и директрисой, получим: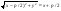

->

Получим каноническое уравнение параболы, симметричной относительно оси Ох с вершиной в начале координат: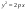

47)Приведение уравнения линии второго порядка к каноническому виду

Если уравнение линии второго порядка не содержит элемента содержащего xy то приведение этого уравнения к каноническому производится путем параллельного переноса. Например нам дано уравнение вида Ax2+By2+Cx+Dy+F=0.

Задача перехода данного уравнения каноническому виду сводится к выделения полных квадратов (x2±2*x*a+a2=(x±a)2), где а – координаты новой координатной плоскости у/.

48. Полярная система координат.

Полярная система координат характеризуется точкой О на плоскости, называемой ’’полюсом”, и лучом ОР, выходящим из этой точки, называемым ’’полярной осью”. Положение любой точки на плоскости в полярной системе координат задается двумя числами р и ф, т.е. М(р;ф), где р - полярный радиус, ф - полярный угол. Положительным направлением отсчета полярного угла считается отсчет против часовой стрелки. (Рис. 83).



Уравнение линии в полярной системе координат записывается в виде уравнения, связывающего значения полярного угла с величиной полярного радиуса р = р(ф).

49Цилиндрические и конические поверхности. Основные формулы

Поверхностью называется геометрическое место точек, коорди­наты которых удовлетворяют уравнению

F(x,y,z)=0 или z=f(x,y). (1)

Линия в пространстве определяется совокупностью двух урав­нений

{F1(x;y;z)=0,F2(x;y;z)=0;(2)

каждое из которых определяет некоторую поверхность.

Цилиндрические поверхности

Цилиндрической поверхностью называется поверхность, описы­ваемая прямой (образующей), параллельной данному направлению и пересекающей данную линию (направляющую).

Всякая цилиндрическая поверхность, образующие которой па­раллельны оси Oz (соответственно Оу, Ох), может быть представле­на уравнением

F(x,y)=0 или y=f(x), (3)

(соответственно

F(x,z)=0 или z=f(x); F(y,z)=0 или z=f(y).

На плоскости хОу уравнение F(x,y)=0 или y=f(x), опреде­ляет линию, которая является направляющей этой цилиндрической поверхности.

Если уравнения направляющей искомой цилиндрической поверх­ности заданы в виде

{F1(x;y;z)=0

,F2(x;y;z)=0

то уравнения образующих этой поверхности будут

(X−x)/m=(Y−y)/n=(Z−z)/p,(5)

где (х,у,z) — точка, принадлежащая направляющей (4); m, n, p — направляющие коэффициенты образующих; X, Y, Z — текущие координаты цилиндрической поверхности. Исключая х, у, z из четырех уравнений (4) и (5), получим ис­комое уравнение цилиндрической поверхности.

Конические поверхности

Конической поверхностью называется поверхность, описываемая прямой, проходящей через данную точку — вершину конуса — и пересекающей данную линию — направляющую конуса.

Если уравнения направляющей искомой конической поверхности заданы в виде

{F1(x;y;z)=0,F2(x;y;z)=0;(8)

то уравнения образующих этой поверхности будут:

X−x0/x−x0=Y−y0/y−y0=Z−z0/z−z0,(9)

где (x;у;z) — точка, принадлежащая направляющей (8),

(x0,y0,z0) — данная точка — вершина конуса;

Х; У; Z — текущие координаты конической поверхности.

Исключая x; у; z из четырех уравнений (8) и (9), получим иско­мое уравнение конической поверхности.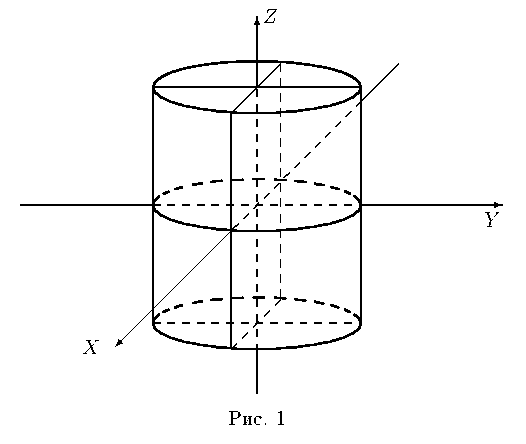



50.Эллипсоидом (вещественным) называется поверхность, имеющая В некоторой («канонической» для нее) прямоугольной системе координат(«каноническое») уравнение

Эллипсоид лежит внутри прямоугольного параллелепипеда



Другими словами, эллипсоиды суть ограниченные поверхности. Все плоские сечения эллипсоида являются поэтому ограниченными кривыми второго порядка, т. е. эллипсами.

Общий вид эллипсоида изображен на рис. 205.


однополостный гиперболоид имеет уравнение



а правильный двуполостный — уравнение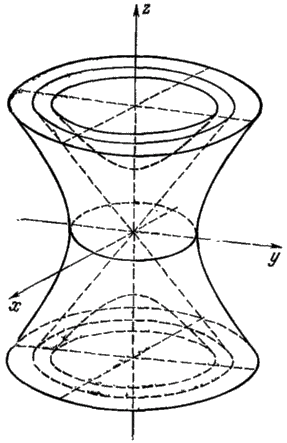





51. Параболоид Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением  a > 0, b > 0, называется эллиптическим параболоидом.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением 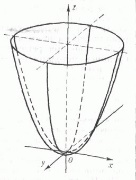 a > 0, b > 0, называется гиперболическим параболоидом.