1. Частные виды матриц. Умножение матриц, свойства
 Скачать 296.98 Kb. Скачать 296.98 Kb.
|
|
Определение 1. Минор матрицы называется базисным , если он неравен 0, и окаймляющие его миноры либо все равны 0, либо совсем отсутствуют. Теорема о базисном миноре. Столбцы матрицы, пересекающие главный минор линейно независимы; Всякий столбец через них линейно выражается. Определение 2. Всякая максимальная линейно независимая система решений однородной системы уравнений (1), называется фундаментальной системой решений (ФСР). Теорема: Если ранг r , матрицы из коэффициентов системы линейных однородных уравнений (1), меньше m, то всякая ФСР системы (1) состоит из n-r решений. Пример №1. Дана однородная система линейных алгебраических уравнений Найти ФСР и общее решение системы. 1.Составим матрицу системы. 2. Легко показать, что ранг матрицы A=2, значит ФСР состоит из трех решений (5-2=3). 3. В матрице A возьмем базисный минор (минор второго порядка): 4. Отбрасываем последние уравнения системы , а неизвестные считаем «свободными» и переносим их в правую часть уравнений. Получим: 5. Ищем первое базисное решение X , для этого положим Определителем матрицы системы является базисный минор, он отличен от 0, значит система (3) имеет единственное решение: Таким образом 6. Полагая в системе (2) 7. Полагая: 8. Итак, ФСР получена; построенная таким образом ФСР называется нормальной. 9. Столбцы 10.Теперь выпишем общее решение исходной однородной системы линейных алгебраических уравнений. 21. Линейное пространство Линейным пространством над полем действительных чисел называется множество L, на котором определены операции сложения и умножения на произвольное действительное число так, что выполнены требования (они называются аксиомами линейного пространства): 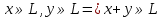 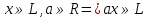 Так, что выполнены требования (аксиомы линейного пространства) 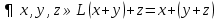 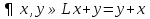 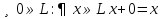 22. Линейные преобразования координат. Будем говорить, что на множестве векторов R задано преобразование А, если каждому вектору х Определение 9.1. Преобразование А называется линейным, если для любых векторов хи у и для любого действительного числа λ выполняются равенства: А(х + у)=Ах + Ау, А(λх) = λ Ах. (9.1) Определение 9.2. Линейное преобразование называется тождественным, если оно преобразует любой вектор хв самого себя. Тождественное преобразование обозначается Е: Ех = х. Рассмотрим трехмерное пространство с базисом е1, е2, е3, в котором задано линейное преобразование А. Применив его к базисным векторам, мы получим векторы Ае1, Ае2, Ае3, принадлежащие этому трехмерному пространству. Следовательно, каждый из них можно единственным образом разложить по векторам базиса: Ае1 = а11 е1 + а21е2 +а31е3, Ае2 = а12 е1 + а22е2 + а32е3, (9.2) Ае3 = а13е1 + а23е2 + а33е3 . Матрица Замечание. Очевидно, что матрицей тождественного преобразования является единичная матрица Е. Для произвольного вектора х =х1е1 + х2е2 + х3е3 результатом применения к нему линейного преобразования А будет вектор Ах, который можно разложить по векторам того же базиса:Ах =х`1е1 + х`2е2 + х`3е3, где координаты x`i можно найти по формулам: х`1 = a11x1 + a12x2 + a13x3, x`2 = a21x1 + a22x2 + a23x3, (9.3) x`3 = a31x1 + a32x2 + a33x3. Коэффициенты в формулах этого линейного преобразования являются элементами строк матрицы А. Преобразование матрицы линейного преобразования при переходе к новому базису. Рассмотрим линейное преобразование А и два базиса в трехмерном пространстве: е1, е2, е3и е1, е2, е3. Пусть матрица С задает формулы перехода от базиса {ek} к базису {ek}. Если в первом из этих базисов выбранное линейное преобразование задается матрицей А, а во втором – матрицей А, то можно найти связь между этими матрицами, а именно: А = С-1АС (9.4) Действительно, 23. Собственный вектор и собственное значение матрицы. Определение: Ненулевой вектор x называется собственным вектором A, если существует действительное число t такое, что A(x) = tx. Действительное число t называется собственным значением или собственным числом оператора A, если существует ненулевой вектор x такой, что выполнено равенство . При наличии равенства мы будем называть x собственным вектором, относящимся к собственному значению t, а t — собственным значением, относящимся к собственному вектору x. 24. Векторы, линейные операции над векторами. . Вектором именуется направленный отрезок прямой, который характеризуется направлением и длиной Одна точка такого отрезка является началом, а другая граничная тока — концом вектор. Вектор обозначается Нуль-вектором именуется вектор, в котором конец совпадает с его началом. О: Коллинеарными именуются векторы, которые расположены на параллельных (к примеру, на одной) прямых, а компланарными называются векторы, которые находятся в параллельных плоскостях. О: Равными являются векторы, которые: 1) коллинеарны; 2) направлены одинаково ( то есть сонаправлены — ); 3) обладают равными модулями. Таким образом, существует возможность переноса вектора параллельно самому себе, при перемещении начала Линейные операции, выполняемые над векторами: сложение, вычитание и умножение на число. Суммой Свойства сложения векторов: 10. Переместительный закон (коммутативность): Доказательство выводится из рисунка 2.2, б. На этом же рисунке показано правило параллелограмма при сложении векторов 20. Сочетательный закон: Доказательство выводится из рис. 2.3. На этом же рисунке дано правило сложения нескольких векторов, в случае когда начало следующего вектора совмещается с концом предыдущего. Сумма представляет собой вектор, который соединяет начало первого вектора с концом последнего слагаемого вектора. Вычитание векторов Разностью Умножение вектора на число. Произведением вектора 10. Сочетательное свойство (ассоциативность): 20. Распределительное свойство (дистрибутивность): Свойства легко проверяются геометрически. 25. Базис — упорядоченный набор векторов в векторном пространстве. Любой вектор в одномерном, двумерном и трёхмерном пространствах можно разложить на один, два или три базисных вектора соответственно. В пространстве за базис можно взять любые 3 неколлинеарных вектора. 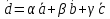 Альфа, Бета и Гамма – координаты данного вектора d в система в системе координат с базисами a, b и c. 26. Расположение точки P на плоскости определяется декартовыми координатами с помощью пары чисел (x,y) или тремя числами (x,y,z) В полярной системе координат, применяемой на плоскости, положение точки P определяется её расстоянием до начала координат r = |OP| и углом «φи» её радиус-вектора к оси Ox Аффинная система координат — прямолинейная система координат в аффинном пространстве. На плоскости задается точкой начала координат О и двумя упорядоченными не коллинеарными векторами, которые представляют собой аффинный базис. Осями координат в данном случае называются прямые, проходящие через точку начала координат параллельно векторам базиса, которые, в свою очередь, задают положительное направление осей. В трехмерном пространстве, соответственно, аффинная система координат задается тройкой линейно независимых векторов и точкой начала координат. Для определения координат некоторой точки М вычисляются коэффициенты разложения вектора ОМ по векторам базиса 27. Линейная зависимость векторов Линейной комбинацией векторов Линейная комбинация векторов образуется из них с помощью операций умножения на число и сложения, следовательно, она также является вектором. Числа Если линейная комбинация Если линейная комбинация называется линейно независимой. Теорема 1.1. Система векторов Теорема 1.2. Если среди векторов Теорема 1.3. Если часть векторов системы векторов 28. Проекции вектора, свойства. Проекции вектора на ось – это вектор, началом и концом которого являются соответственно проекции начала и конца заданного вектора. Числовая проекция вектора на ось – это число, которое равно произведению длины данного вектора на косинус угла между этим вектором и вектором, определяющим направление оси. Чтобы построить проекцию вектора AB на ось L нужно из точек A и B опустить перпендикуляры на направленную прямую L - основания этих перпендикуляров дадут начало и конец искомой проекции Пр l¯AB В этих обозначениях определение числовой проекции вектора Итак, мы имеем первую формулу для вычисления числовой проекции вектора: 29)Скалярное произведение векторов Геометрическая интерпретация. a · b = |a| · |b| cos α Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b. a · b = a1 · b1 + a2 · b2 + ... + an · bn. Свойства скалярного произведения векторов 1)Скалярное произведение вектора самого на себя всегда больше или равно нуля:a · a ≥ 0 2)Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору:a · a = 0 <=> a = 0 3)Скалярное произведение вектора самого на себя равно квадрату его модуля:a · a = |a|2 4)Операция скалярного умножения коммуникативна:a · b = b · a 5)Если скалярное произведение двух не нулевых векторов равно нулю, то эти вектора ортогональны: a ≠ 0, b ≠ 0, a · b = 0 <=> a ┴ b 6)(αa) · b = α(a · b) 7)Операция скалярного умножения дистрибутивна: (a + b) · c = a · c + b · c 30)Векторное произведение векторов Векторное произведение двух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат - это вектор, значение которого можно вычислить, используя следующие формулы:
Свойства векторного произведения векторов Геометрический смысл векторного произведения. Модуль векторного произведения двух векторов a и b равен площади параллелограмма построенного на этих векторах:Sпарал = [a × b] Геометрический смысл векторного произведения. Площадь треугольника построенного на векторах a и b равна половине модуля векторного произведения этих векторов:
31Смешанное произведение Викторов Смешанным произведением векторов a, b и c называется число, равное скалярному произведению вектора a→ на векторное произведение векторов b и c. Геометрический смысл: Смешанное произведение равно объему параллелепипеда, построенного на трех векторах(не комланарных (V=0)). Свойства: 1. Смешанное произведение не меняется при циклической перестановке перемножаемых векторов (т.е. a встает на место b, b встает на место c, c встает на место а и т.д.((a,b,c) переходит в (c,a,b)(они равны)) 2. Смешанное произведение меняет знак при перестановке двух векторов 3. Смешанное произведение равно нулю, если векторы компланарны (если два вектора равны, то произведение также равно нулю) Если три смешанное произведение трех векторов положительно их называют Правая тройка векторов, если отрицательная, то левая тройка векторов. Вычисление: Смешанное произведение кратко можно записать в виде определителя 3 – го порядка, строки которого являются координаты перемножаемых векторов Приложение смешанного произведения 1. Объемы параллелепипеда(1) и пирамиды(2): V1=(a,b,c) ; V2= 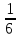 (a,b,c) . (a,b,c) .2. Линейная независимость трех векторов: Если смешанное произведение не равно нулю, то совокупность векторов является линейно независимой и образует базис в пространстве (т.е.некомланарны) и наоборот, если смешанное произведение равно нулю, то совокупность векторов не является линейно независимой и не образует базис в пространстве (т.е. комланарны). 32 Условия коллинеарности, компланарности и перпендикулярности векторов Условия коллинеарности векторов Два вектора будут коллинеарны при выполнении любого из этих условий: 1. Два вектора a и b коллинеарны, если существует число n такое, что a = n · b 2. Два вектора коллинеарны, если отношения их координат равны( 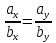 ). Условие 2 неприменимо, если один из компонентов вектора равен нулю. ). Условие 2 неприменимо, если один из компонентов вектора равен нулю.3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору. Условие 3 применимо только для трехмерных (пространственных) задач. Условия компланарности векторов 1.Векторы компланарны если их смешанное произведение равно нулю. 2.Векторы компланарны если они линейно зависимы (коллинеарны). Условие перпендикулярности векторов Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю( 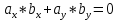 ). ).33.Прямая и линия на плоскости, ее общее ур-ие и его исследование.Уравнением линии (или кривой) на плоскости 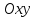 называется такое уравнение называется такое уравнение 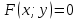 c двумя переменными, которому удовлетворяют координаты c двумя переменными, которому удовлетворяют координаты 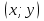 каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на линии каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на линии A(x – x0) + B(y – y0) = 0 называ- ют уравнением прямой, проходящей через точку M0(x0;y0) перпендикулярно вектору N̄ = {A; B} (в векторной и коорди- натной форме соответственно). Уравнения (r̄ , N̄) + C = 0 и Ax + By + C = 0 называют общим уравнением прямой на плоскости (в векторной и координатной форме соответственно). Исследование Если в уравнении Ax+By+C = 0 все коэффициенты A,B и C отличны от нуля, то уравнение называют полным; если хотя бы один из коэффициентов равен нулю – уравнение называют неполным. A и B – ненулевые, а C = 0, т.е. уравнение прямой имеет вид Ax+By = 0. Такая прямая проходит через начало координат O(0;0). Пусть в общем уравнении прямой C = 0 и один из коэф- фициентов A или B тоже нулевой, т.е. уравнение прямой имеет вид Ax = 0 или By = 0. Эти уравнения можно записать в виде x = 0 (уравнения координатной оси Oy) и y = 0 (уравнения координатной оси Ox). 34.Вывести параметрическое и каноническое ур-ие прямой на плоскости. Вектор, параллельный прямой, называют направляющимвектором этой прямой. Уравнение r̄ = r̄ + t S и систему уравнений называют параметрическими уравнениями прямой (в векторной и координатной форме соответственно). Каноническое уравнение прямой на плоскости Вектор s не параллелен ни одной из координатных осей (т.е. m 0 и n 0). Уравнение 35 Общее уравнение плоскости, вывод, исследование Всякая поверхность в пространстве задается в декартовых координатах как функция f(x, y, z)=0 Всякая поверхность первого порядка – плоскость, отсюда: Ax+By+Cz+D=0 Общее уравнение плоскости N{A; B; C} Нормальный вектор плоскости 36 Уравнение плоскости через три точки, вывод Дано: 3 точки M1(x1,y1,z1); M2(x2,y2,z2); M3(x3,y3,z3) 1 способ Уравнение A(x-x1)+B(y-y1)+C(z-z1)=0 – плоскость, проходящая через точку M1(x1,y1,z1) Находим коэффициенты A, B, C из условия N={A, B, C} N перпендикулярен двум векторам М1М2 и М1М3 2 способ 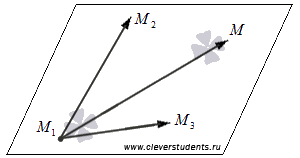 Берем случайную точку в плоскости M(x, y, z) Векторы М1М2, М1М3, М1М должны быть компланарны, поэтому Скалярное произведение рано 0 М1М2 * М1М3 * М1М=0 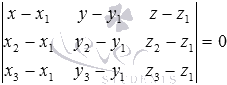 Раскрываем определитель, получаем уравнение плоскости. |

