математика. Тема 1. 1. Что называется функцией
 Скачать 194.21 Kb. Скачать 194.21 Kb.
|
|
1. Что называется функцией? Функцией называется правило, по которому каждой переменной 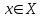 соответствует одно и только одно значение соответствует одно и только одно значение 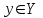 . . Функция обозначается 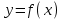 или или 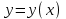 или или 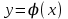 . .Переменная x – независимая переменная или аргумент функции; переменная y – зависимая переменная или значение функции. 2. Что такое область определения и область значений функции? Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох. Чтобы обозначить область определения некоторой функции y, используют запись D(y). 3. Перечислите способы задания функций, их достоинства. Используют следующие способы задания функции: 1.Аналитический способ – задание функций с помощью формул. Например, 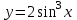 , , 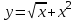 . .2.Графический способ – задание функций с помощью графика. Например, 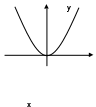 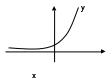 3.Табличный способ – задание функций с помощью таблиц. Например,
4. Словесный способ – задание функций с помощью алгоритма вычисления. Например, 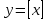 - целая часть числа х. - целая часть числа х.Целая часть числа х – это ближайшее целое число, не превосходящее самого числа х. 4. Перечислите основные свойства функций. Свойства функций приведены в таблице:
5. Дайте определение предела функции в точке. Число А называется пределом функции y=f(х) при х, стремящемсяк а, если для любой последовательности чисел х1, х2, х3, …, .хn ,… сходящейся к числу а, следует, что последовательность значений функции f(х1), f(х2),…, f(хn)… сходится к числу А. Предел функции в точке а обозначается 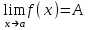 . .6. Какая функция называется непрерывной в точке? Функция f(x) называется непрерывной в точке x0, если она определена на некоторой окрестности U(x0) этой точки, включая саму точку, и если предел при x стремящемся к x0 существует и равен значению функции в x0: 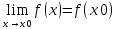 Здесь подразумевается, что x0 – это конечная точка. Значение функции в ней может быть только конечным числом. 7. Сформулируйте основные свойства пределов. 1. Функция не может иметь более одного предела (при одной и той же базе). 2. Предел постоянной равен самой этой постоянной: 3. Предел суммы функций равен сумме пределов этих функций: 4. Предел произведения функций равен произведению пределов этих функций: Отсюда следует, что постоянный множитель можно выносить за знак предела: 5. Предел частного двух функций равен частному пределов этих функций (если предел делителя неравен нулю): 6. (свойство предела сложной функции) Если 7. Если при базе В (т.е. в некоторой окрестности точки х0или при достаточно больших х) f1(х) < f2(х), то 8. Как раскрывается неопределенность вида 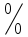 , , 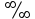 ? ?При вычислении пределов при 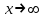 основные теоремы о пределах сохраняют силу и, кроме того, используются правила: основные теоремы о пределах сохраняют силу и, кроме того, используются правила:а) чтобы раскрыть неопределенность типа 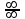 , необходимо числитель и знаменатель дроби разделить на наибольшую степень переменной; , необходимо числитель и знаменатель дроби разделить на наибольшую степень переменной;б) чтобы раскрыть неопределенность типа 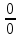 , необходимо числитель и знаменатель дроби разделить на наименьшую степень переменной ; , необходимо числитель и знаменатель дроби разделить на наименьшую степень переменной ;в) чтобы раскрыть неопределенность типа 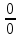 , иногда достаточно числить и знаменатель дроби разложить на множители и затем сократить дробь на множитель, приводящий к неопределенности; , иногда достаточно числить и знаменатель дроби разложить на множители и затем сократить дробь на множитель, приводящий к неопределенности;г) чтобы раскрыть неопределенность типа 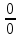 , зависящую от иррациональности, достаточно перевести иррациональность из числителя в знаменатель или из знаменателя в числитель и сократить на множитель, приводящий к неопределенности; , зависящую от иррациональности, достаточно перевести иррациональность из числителя в знаменатель или из знаменателя в числитель и сократить на множитель, приводящий к неопределенности;д) чтобы раскрыть неопределенность типа 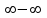 , необходимо числитель и знаменатель дроби одновременно умножить на сопряженное выражение и тем самым свести к неопределенности вида , необходимо числитель и знаменатель дроби одновременно умножить на сопряженное выражение и тем самым свести к неопределенности вида 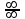 или или 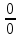 . . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

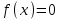 .
.
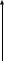

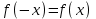



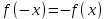 .
.




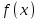 называется возрастающей, если большему значению аргумента соответствует большее значение функции, т.е.
называется возрастающей, если большему значению аргумента соответствует большее значение функции, т.е.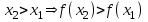


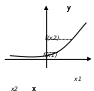
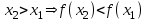
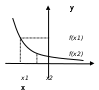
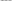
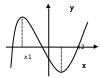
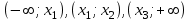
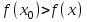 .
.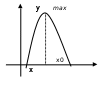
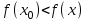 .
.

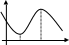

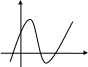
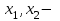 точки локального экстремума.
точки локального экстремума.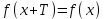 .
.

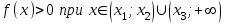
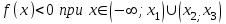
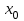 , если предел функции при
, если предел функции при 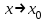 равен значению функции в этой точке, т.е.
равен значению функции в этой точке, т.е.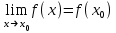 .
.