Эконометрика. ЭКОНОМЕРИКА. 1 Дайте определение эконометрики на основе сложившихся подходов

• Название: 1 Дайте определение эконометрики на основе сложившихся подходов
• Анкор: Эконометрика
• Дата: 21.06.2022
• Размер: 94.18 Kb.
• Имя файла: ЭКОНОМЕРИКА.docx
• Тип: Закон; #607693
• страница: 3 из 3

22.Какова концепция F-критерия Фишера?
F-критерий Фишера – это один из важных статистических критериев, используемых при проверке значимости как уравнения регрессии в целом, так и отдельных его коэффициентов.

Критерий Фишера позволяет сравнивать величины выборочных дисперсий двух рядов наблюдений.

F - критерий Фишера является параметричесикм критерием и используется для сравнения дисперсий двух вариационных рядов. Эмпирическое значение критерия вычисляется по формуле: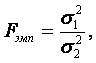



где   - большая дисперсия,   - меньшая дисперсия рассматриваемых вариационных рядов.

Если вычисленное значение критерия F_эмп больше критического для определенного уровня значимости и соответствующих чисел степеней свободы для числителя и знаменателя, то дисперсии считаются различными. Иными словами, проверяется гипотеза, состоящая в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой: H₀={D_x=D_y}.

Критическое значение критерия Фишера следует определять по специальной таблице, исходя из уровня значимости α и степеней свободы числителя (n₁-1) и знаменателя (n₂-1).
23.Как оценивается значимость параметров уравнения регрессии?

Оценить значимость уравнения регрессии — значит установить, соответствует ли математическая, модель, выражающая зависимость между Y и X, экспериментальным данным. Для оценки значимости в предпосылках «нормальной регрессии» проверяют гипотезу 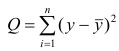  Если она отвергается, то считают, что между Y и X нет связи (или связь нелинейная). Для проверки нулевой гипотезы используют основное положение дисперсионного анализа о разбиении суммы квадратов на слагаемые. Воспользуемся разложением  - Общая сумма квадратов отклонений результативного признака

 разлагается на   (сумму, характеризующую влияние признака

X) и   (остаточную сумму квадратов, характеризующую влияние неучтённых факторов). Очевидно, чем меньше влияние неучтённых факторов, тем лучше математическая модель соответствует экспериментальным данным, так как вариация У в основном объясняется влиянием признака X.

Для проверки нулевой гипотезы вычисляют статистику 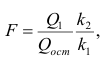  которая имеет распределение Фишера-Снедекора с А  степенями свободы (в п - число наблюдений). По уровню значимости а и числу степеней свободы   находят по таблицам F-распределение для уровня значимости а=0,05 критическое значение  удовлетворяющее условию  . Если  нулевую гипотезу отвергают, уравнение считают значимым. Если   то нет оснований отвергать нулевую гипотезу.

24.Приведите примеры моделей нелинейных относительно включаемых переменных и нелинейных относительно оцениваемых параметров.

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций: например, равносторонней гиперболы , параболы второй степени и д.р.

Различают два класса нелинейных регрессий:

• регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;

• регрессии, нелинейные по оцениваемым параметрам.

Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции:

1. полиномы разных степеней

2. равносторонняя гипербола

К нелинейным регрессиям по оцениваемым параметрам относятся функции:

-степенная

- показательная

- экспоненциальна

25.В чем смысл средней ошибки аппроксимации и как она определяется?

Средняя ошибка аппроксимации среднее отклонение расчетных значений от фактических. Допустимый предел значений средней ошибки аппроксимации не более 8-10% Средний коэффициент эластичности показывает, на сколько процентов изменится результат (результативный признак) от своей средней величины при изменении фактора x (признак-фактор) на 1% от своего среднего значения. Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитывается t-критерий Стьюдента. Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.

Отклонения можно рассматривать как абсолютную ошибку аппроксимации, а - как относительную ошибку аппроксимации.

Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению определяют среднюю ошибку аппроксимации: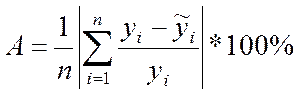

 

                        (25)

 

Фактическое значение результативного признака y отличается от теоретических значений, рассчитанных по уравнению регрессии. Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим, и лучше качество модели.

Величина отклонений фактических и расчетных значений результативного признака по каждому наблюдению представляет собой ошибку аппроксимации.

Поскольку может быть, как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.

Если А до 10-12%, то можно говорить о хорошем качестве модели.
26.Как проводится подбор линеаризующего преобразования для нелинейных моделей?

Линеаризация – это преобразование. Оно осуществляется для того, чтобы упростить определенные модели и вычисления. Например, применение логарифма к обеим частям линейной регрессии позволяет оценить неизвестные параметры более простым способом. Но использование нелинейного изменения уравнения требует осторожности. Это связано с тем, что данные будут изменяться. Поэтому появятся ошибки модели. Их интерпретация может привести к ошибочному суждению о гипотезе. Обычно в нелинейных уравнениях используется модель Гаусса для исследования ошибок, что необходимо учитывать при проверке. В которых случаях применяется уравнение Лайнуивер – Берк(Это так называемый метод двойных обратных величин. Для линеаризации необходимо взять обратные величины от левой и правой частей уравнения), либо обобщенная линейная модель. Чтобы уточнить построенную модель и снизить вероятность ошибок, независимая переменная разбивается на классы. Вследствие этого линейная регрессия разбивается посегментно. Она может дать результат, в котором будет видно, как ведет себя параметр в зависимом положении. Отображение изменений производится графически. То есть сущность линеаризации заключается в том, что исследователь применяет особые методики для того, чтобы провести преобразования исходных данных. Это позволяет исследовать нелинейную зависимость. Переменные нелинейного уравнения преобразуются с помощью специальных методик в линейные. Это может привести к ошибкам, что необходимо учитывать в процессе преобразования уравнения. Метод может быть опасным, так как влияет на результат вычислений. Сущность метода заключается в том, что нелинейные переменные заменяются линейными. Регрессия сводится к линейной. Такой подход часто используется для полиномов. Далее применяются известные и простые оценки исследования линейных регрессии. Но изменение полиномов должно так же проводиться с осторожностью. Чем выше порядок полинома, тем сложнее удержаться в рамках реалистичной интерпретации коэффициентов регрессии. В логарифмических моделях составляется линейная модель с новыми переменными. Оценка результата происходит с помощью метода наименьших квадратов. Эта методика подходит для исследования кривых спроса и предложения, производственных функций, кривых освоения связи между трудоемкостью и производственными масштабами. Такой подход актуален при запуске новых видов продукции.
27. Дайте определение коэффициенту детерминации.

Коэффициент детерминации (R2)— это доля объяснённой дисперсии отклонений зависимой переменной от её среднего значения. Зависимая переменная объясняется (прогнозируется) с помощью функции от объясняющих переменных, в частном случае является квадратом коэффициента корреляции между зависимой переменной и её прогнозными значениями с помощью объясняющих переменных. Тогда можно сказать, что R2 показывает, какая доля дисперсии результативного признака объясняется влиянием объясняющих переменных.

Формула для вычисления коэффициента детерминации:



где yi — наблюдаемое значение зависимой переменной, а fi — значение зависимой переменной предсказанное по уравнению регрессии   -среднее арифметическое зависимой переменной.
28.Какова область определения коэффициента детерминации?
Коэффициент детерминации для модели с константой принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это интерпретируется как соответствие модели данным. Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50 % (в этом случае коэффициент множественной корреляции превышает по модулю 70 %). Модели с коэффициентом детерминации выше 80 % можно признать достаточно хорошими (коэффициент корреляции превышает 90 %). Значение коэффициента детерминации 1 означает функциональную зависимость между переменными.
29. Дайте определение понятию гомоскедастичности (гетероскедастичности) случайных возмущений.

Под гомоскедастичностью понимается предположение о том, что дисперсия случайной ошибки βi является известной постоянной величиной для всех наблюдений.

Но на практике предположение о гомоскедастичности случайной ошибки βi или остатков модели регрессии ei выполняется не всегда.

Под гетероскедастичностью (heteroscedasticity – неоднородный разброс) понимается предположение о том, что дисперсии случайных ошибок являются разными величинами для всех наблюдений, что означает нарушение второго условия нормальной линейной модели множественной регрессии
30. Каковы возможные причины возникновения гетероскедастичности.

Причины гетероскедастичности

- Неоднородность исследуемых объектов (напр, при анализе зависимости спроса от дохода потребителя выясняется, что чем больше доход, тем больше индивидуальное значение спроса колеблется относительно ожидаемого значения)

- Характер наблюдений (напр, данные временного ряда)

31.Каковы последствия гетероскедастичности

Последствия гетероскедастичности

Последствия нарушения условия гомоскедастичности случайных возмущений:

1. Потеря эффективности оценок коэффициентов регрессии, т.е. можно найти другие, отличные от МНК и более эффективные оценки.

2. Смещенность стандартных ошибок коэффициентов в связи с некорректностью процедур их оценки. Это, в свою очередь, может привести к некорректности результатов тестирования статистической значимости параметров линейной модели.

При наличии гетероскедастичности МНК (метод наименьших квадратов) обеспечивает несмещенные оценки параметров, но оценка дисперсии возмущений - смешенная, то есть:

Это приводит к неадекватным оценкам:

- Автоковариационной матрицы оценок параметров: С_вв =s²(X^TX)^-1;

- Границ доверительных интервалов параметров модели и значений зависимой переменной, т.е. последствия такие же, как и от автокорреляции.