Эконометрика. ЭКОНОМЕРИКА. 1 Дайте определение эконометрики на основе сложившихся подходов
 Скачать 94.18 Kb.
|
|
15.Понятие выборки наблюдений за поведением объекта. Статистическая методология исследования массовых явлений различает, как известно, два способа наблюдения в зависимости от полноты охвата объекта: сплошное и несплошное. Разновидностью несплошного наблюдения является выборочное. Под выборочным наблюдением понимается такое несплошное наблюдение, при котором статистическому обследованию подвергаются единицы изучаемой совокупности, отобранные случайным способом. Выборочное наблюдение ставит перед собой задачу - по обследуемой части дать характеристику всей совокупности единиц при условии соблюдения всех правил и принципов проведения статистического наблюдения. При выборочном методе обследованию подвергается сравнительно небольшая часть всей изучаемой совокупности (обычно 5-10%). При этом подлежащая изучению статистическая совокупность, из которой производится отбор, называется генеральной совокупностью. Отобранная из генеральной совокупности некоторая часть единиц, подвергающаяся обследованию, называется выборочной совокупностью. Значение выборочного метода состоит в том, что при минимальной численности обследуемых единиц, проведение исследования осуществляется в более короткие сроки и с минимальными затратами труда и средств. Это повышает оперативность статистической информации, уменьшает ошибки регистрации. Поскольку изучаемая совокупность состоит из единиц, с варьирующими признаками, то состав выборочной совокупности отличается от состава генеральной совокупности. Это расхождение между характеристиками выборки и генеральной совокупности составляет ошибку выборки. Она зависит от ряда факторов: степени вариации изучаемого признака, численности выборки, методов отбора единиц в выборочную совокупность, принятого уровня достоверности. Способы определения ошибки выборки при различных приемах формирования выборочных совокупностей и распространение характеристик выборки на генеральную совокупность составляет основное содержание статистической методологии выборочного метода. В статистике применяются различные способы формирования выборочной совокупности. Основным условием проведения выборочного обследования является предупреждения возникновения систематических ошибок, возникающих вследствие нарушения принципа равных возможностей попадания в выборку каждой единицы генеральной совокупности. Это достигается в результате применения научно обоснованных способов формирования выборочной совокупности. На практике используют следующие способы отбора единиц из генеральной совокупности: 1. Индивидуальный отбор - в выборку отбираются отдельные единицы. 2. Групповой отбор - в выборку попадают качественно однородные группы или серии изучаемых единиц. 3. Комбинированный отбор - комбинация индивидуального и группового отбора. Способы отбора определяются правилами формирования выборочной совокупности. Выборка может быть: 1. Собственно-случайная 2. Механическая 3. Типическая 4. Серийная 5. Комбинированная Собственно-случайная. Выборочная совокупность образуется в результате случайного отбора отдельных единиц изучаемой совокупности. Прежде чем производить собственно-случайный отбор, необходимо убедиться, что все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку. Следует также установить четкие границы генеральной совокупности таким образом, чтобы включение или не включение в нее отдельных единиц не вызывало сомнений. Так, например, при обследовании студентов необходимо указать, будут ли приниматься во внимание лица, находящиеся в академическом отпуске, студенты негосударственных вузов, военных училищ и т.п. Механическая выборка. Отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы. Так, при 2-% выборке отбирается каждая 50-я единица. Т.о., в соответствии с принятой долей отбора генеральная совокупность механически разбивается на равновеликие группы. Из каждой группы в выборку отбирается лишь одна единица. Для обеспечения репрезентативности выборки все единицы генеральной совокупности должны располагаться в определенном порядке. При упорядоченной генеральной совокупности по существенному признаку в выборочную совокупность должна отбираться та единица, которая находится в середине каждой группы. Это позволяет избежать систематической ошибки выборки. Типическая выборка. При типической выборке генеральная совокупность расчленяется на однородные типические группы. Из каждой группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность. Репрезентативность типической выборки обеспечивается расчленением на качественно однородные группы. Это обуславливает представительство в выборке каждой типологической группы. Группы образовываются либо методом типической группировки единиц генеральной совокупности, либо могут использоваться уже имеющиеся, естественно сложившиеся группы. Серийная (гнездовая) выборка. При серийной выборке из генеральной совокупности отбираются не отдельные единицы, а целые серии или гнезда. Внутри каждой серии обследуется все без исключения единицы. Практически серийная выборка проводится по схеме бесповторного отбора. Комбинированная выборка. Рассмотренные способы обычно применяются не в чистом виде, а комбинируются. Например, комбинируется серийная и случайная выборка. Генеральная совокупность разбивается сначала на серии, далее в отобранных сериях производится случайный отбор. 16.Идея метода наименьших квадратов. Метод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное. Сущность метода наименьших квадратов заключается в отыскании параметров модели тренда, которая лучше всего описывает тенденцию развития какого-либо случайного явления во времени или в пространстве (тренд – это линия, которая и характеризует тенденцию этого развития). Задача метода наименьших квадратов (МНК) сводится к нахождению не просто какой-то модели тренда, а к нахождению лучшей или оптимальной модели. Эта модель будет оптимальной, если сумма квадратических отклонений между наблюдаемыми фактическими величинами и соответствующими им расчетными величинами тренда будет минимальной (наименьшей): Основная идея данного метода состоит в том, что в качестве критерия точности решения задачи рассматривается сумма квадратов ошибок, которую стремятся свести к минимуму. Параметры модели выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений от модельных была минимальной: 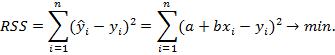 Среди преимуществ метода наименьших квадратов следует особенно отметить лёгкость вычислительной процедуры и хорошие по статистическим свойствам оценки. Данные факты объясняют широкое применение данного метода в статистическом анализе. Из недостатков наиболее существенным является чувствительность к выбросам. 17. Какими свойствами должны обладать случайные возмущения, чтобы с помощью МНК получить несмещенные оценки Величина  называется несмещённой оценкой параметра если её выборочное математическое ожидание равно оцениваемому параметру генеральной совокупности: Отсюда следует, что где ФИi – это величина смещения оценки.Случайная величина  , или возмущение, включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. ЕЕ присутствие в модели обусловлено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.При выполнении условий Гаусса-Маркова указанная модель называется классической нормальной линейной регрессионной моделью. Наряду с условиями Гаусса-Маркова обычно предполагается, что случайный член е, имеет нормальное распределение. При этом требование некоррелированности значений случайного члена эквивалентно их независимости. Первое условие означает, что случайный член не должен иметь систематического смещения. Если постоянный член ( включен в уравнение регрессии, то это условие выполняется автоматически. Второе условие означает, что дисперсия случайного члена в каждом наблюдении имеет только одно значение. Но ее величина заранее неизвестна, и одна из задач регрессионного анализа состоит в ее оценке. Условие независимости дисперсии случайного члена от номера наблюдения называется гомоскедастичностью. Зависимость дисперсии случайного члена от номера наблюдения называется гетероскедастичностью. Существуют специальные методы диагностирования и устранения гетероскедастичности. Третье условие указывает на некоррелированность случайных членов для разных наблюдений. Это условие часто нарушается, когда данные являются временными рядами. В случае когда третье условие не выполняется, говорят об автокорреляции остатков. Если условие независимости случайных членов не выполняется, то оценки коэффициентов регрессии, полученные по МНК, оказываются неэффективными, хотя и несмещенными. Существуют методы диагностирования и устранения автокорреляции. Четвертое условие. Если условие о неслучайности объясняющей переменной не выполняется, то оценки коэффициентов регрессии оказываются смещенными и несостоятельными. Теорема Гаусса-Маркова. Если описанные четыре условия выполняются, то оценки, сделанные с помощью МНК, являются наилучшими оценками. Они обладают свойствами: несмещенности, что означает отсутствие систематической ошибки в положении линии регрессии; эффективности — имеют наименьшую дисперсию в классе всех линейных несмещенных оценок; состоятельности — при достаточно большом объеме данных оценки приближаются к истинным значениям. 18.Свойство гомоскедастичности случайных наблюдений. Гомоскедастичностью называют свойство данных, используемых для построения модели линейной регрессии, которое заключается в том, что их дисперсия вдоль прямой регрессии является постоянной. Гомоскедастичность — одно из условий эффективности регрессионной модели.X Проверка выполнения требования гомоскедастичности случайных остатков может быть произведена визуально, на основе графика остатков, или с помощью специальных критериев. Для проведения визуального анализа необходимо построить график зависимости величин случайных остатков от выровненного значения результирующей переменной. В случае гомоскедастичности "облако" случайных остатков находится в области, параллельной оси абсцисс (рис. 2.2, а). Все прочие случаи соответствуют гетероскедастичности случайных остатков (например, как на рис. 2.2, б). Аналогичные графики можно построить также для зависимости случайных остатков от значений конкретных независимых переменных, входящих в регрессию. В статистике последовательность или вектор случайных величин являются гомоскедастичными, если все случайные величины в последовательности или векторе имеют одинаковую дисперсию. 19.Свойство автокорреляции случайных возмущений Автокорреляция случайного возмущения – невыполнение 3 предпосылки теоремы Гаусса-Маркова о независимости случайных переменных в уравнениях наблюдений (ковариация 2 случайных переменных = 0). Если же предпосылка выполняется, то идет речь об отсутствии автокорреляции. В классической регрессионной модели выполнение третьего условия Гаусса-Маркова (Соv(εt εS) = 0,при t ≠ s) гарантирует некоррелированность значений случайных членов в различные моменты наблюдений и это позволяет получить несмещенные МНК-оценки с минимальной дисперсией. Зависимость значений случайных членов в различные моменты времени называется автокорреляцией (сериальной корреляцией). Формальной причиной автокорреляции в регрессионных моделях является нарушение третьего условия теоремы Гаусса-Маркова, действительной же причиной может быть: неправильная спецификация переменных (пропуск важной объясняющей переменной); наличие неучтенных факторов; использование ошибочной функциональной зависимости, а иногда и характер наблюдений (например, временные ряды). Для проверки на автокорреляцию используется ряд критериев, из которых наиболее широкое применение получил критерий Дарбина-Уотсона Последствия автокорреляции в определенной степени сходны с последствиями гетероскедастичности. Среди них при применении МНК обычно выделяются следующие: 1. Оценки параметров, оставаясь линейными и несмещенными, перестают быть эффективными. Следовательно, они перестают обладать свойствами наилучших линейных несмещенных оценок 2. Дисперсии оценок являются смещенными. Зачастую дисперсии, вычисляемые по стандартным формулам, являются заниженными, что приводит к увеличению t-статистик. Это может привести к признанию статистически значимыми объясняющие переменные, которые в действительности таковыми могут и не являться. 3. Оценка дисперсии регрессии  является смещенной оценкой истинного значения  , во многих случаях занижая его.4. В силу вышесказанного выводы по t- и F-статистикам, определяющим значимость коэффициентов регрессии и коэффициента детерминации, возможно, будут неверными. Вследствие этого ухудшаются прогнозные качества модели. 20. Что понимается под понятием «качество спецификации модели»? Спецификация модели– это математическая форма записи уравнения зависимости результирующей переменной от одного или нескольких факторов. По сути, она представляет собой отбор факторов, включаемых в модель, и выбор вида уравнения регрессии. В зависимости от спецификации эконометрических моделей классифицируют на несколько типов. Под качеством спецификации модели понимается: - качество выбора функции уравнения регрессии; - качество выбора набора регрессоров (факторов) Другими словами: насколько правильно предположение, что поведение эндогенной переменной зависит от значения фактора Х. 21. В чем состоит смысл коэффициента регрессии, каковы способы его оценивания? Регрессия — функция, позволяющая по средней величине одного признака определить среднюю величину другого признака, корреляционно связанного с первым. С этой целью применяется коэффициент регрессии и целый ряд других параметров. Например, можно рассчитать число простудных заболеваний в среднем при определенных значениях среднемесячной температуры воздуха в осенне-зимний период. Коэффициент регрессии — абсолютная величина, на которую в среднем изменяется величина одного признака при изменении другого связанного с ним признака на установленную единицу измерения. Формула коэффициента регрессии. Rу/х = rху x (σу / σx) где Rу/х — коэффициент регрессии; rху — коэффициент корреляции между признаками х и у; (σу и σx) — среднеквадратические отклонения признаков x и у. Проверить значимость оценок коэффициентов регрессии — значит установить, достаточна ли величина оценки для статистически обоснованного вывода о том, что коэффициент регрессии отличен от нуля. Для этого проверяют гипотезу о равенстве нулю коэффициента регрессии, соблюдая предпосылки «нормальной регрессии». В общем случае коэффициент регрессии k показывает, как в среднем изменится результативный признак ( Y ), если факторный признак ( X ) увеличится на единицу . Свойства коэффициента регрессии • Коэффициент регрессии может принимать любые значения. • Коэффициент регрессии не симметричен , т.е. изменяется, если X и Y поменять местами. • Единицей измерения коэффициента регрессии является отношение единицы измерения Y к единице измерения X : ([ Y ] / [ X ]). • Коэффициент регрессии изменяется при изменении единиц измерения X и Y . Чем больше абсолютное значение коэффициента регрессии, тем значительнее влияние факторного признака на результативный признак. Знак коэффициента регрессии говорит о характере влияния на результативный признак. Если коэффициент регрессии имеет знак плюс, то с увеличением фактора результатный признак возрастает. Если коэффициент регрессии имеет знак минус, то с его увеличением результативный признак уменьшается. |