Технологии программирования. Базовый курс. 1. Для каких случаев производят оценку быстродействия алгоритма
 Скачать 263.63 Kb. Скачать 263.63 Kb.
|
|
1. Для каких случаев производят оценку быстродействия алгоритма? При обработке большого объема информации. При сравнении различных алгоритмов. Для предсказания времени выполнения программы и поиска наиболее эффективного решения поставленной задачи. 2. Что такое скорость роста алгоритма? Скорость роста алгоритма - это скорость роста числа операций при росте объема входных данных. 3. Классификация скоростей роста алгоритма. О (“о”) большое: Алгоритмы, сложность которых растет не быстрее данной функции. Ω (омега) большое: Алгоритмы, сложность которых растет по крайней мере так же быстро, как данная функция. Θ (тета) большое: Алгоритмы, сложность которых растет с той же скоростью. Временная сложность алгоритма - f, которая показывает t, необходимое на выполнение данного алгоритма при заданном V входящих данных (n). Оценивается количеством элементарных операций, выполняемых алгоритмом. В худшем случае - макс количество элементарных операций В наилучшем случае - мин количество. 5. Что такое пространственная сложность алгоритма? Пространственная сложность – это критерий оценки алгоритма. Это есть зависимость n занимаемой памяти от V входных данных (n). 6. Какая структура данных называется односвязным списком? Цепочка элементов, каждый элемент которой имеет ссылку на следующий. 7. Какая структура данных называется двусвязным списком? Цепочка элементов, каждый элемент которой имеет ссылку на следующий и предыдущий элементы. 8. Какая структура данных называется циклическим списком? Представляет собой односвязный или двусвязный список, где только последний и первый элементы имеют ссылки на себя. 9. Какая структура данных называется стеком? Стек — структура по принципу "последний пришёл — первый ушёл" (LAST IN - FIRST OUT). 10. Какая структура данных называется очередью? Очередь — структура по принципу “первый вошел — первым вышел” (FIRST IN - FIRST OUT) 11. Какая структура данных называется очередью по приоритету? Это структура данных, где у каждого элемента есть приоритет. Элемент с более высоким приоритетом добавляется перед элементом с более низким, если P1=P2, то элементы располагаются в зависимости от своей позиции в очереди. Элемент с самым высоким приоритетом удаляется в первую очередь. 12. Какая структура данных называется двусторонней очередью (деком)? Дек или двусторонняя очередь - структура данных, в которой можно добавлять и удалять элементы с двух сторон. 13. Какая матрица называется разреженной? Разреженная матрица – это матрица, в которой подавляющее большинство элементов равно нулю. 14. Как хранятся матрицы общего вида? Координатная форма хранения – в такой форме данные хранятся в виде 3 массивов: A – Ненулевые значения; LI – Номера строк; LJ–Номера столбцов. 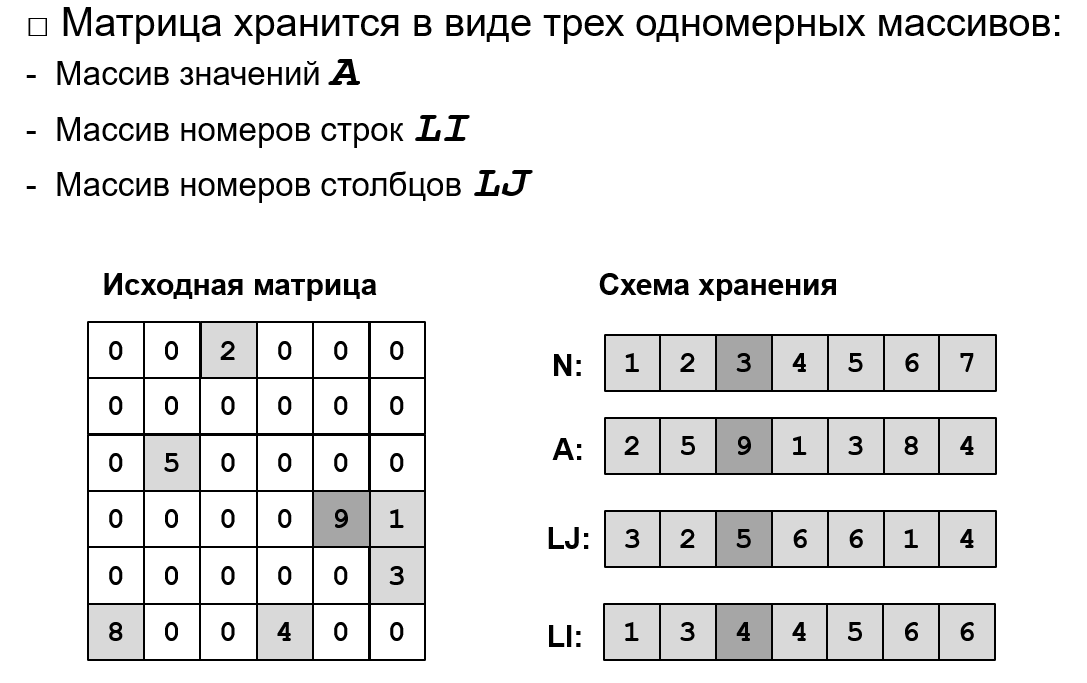 Разреженный строчный формат. Матрица хранится в 3 одномерных массивах: A – Построчно сверху вниз; LJ–Номера столбцов; LI – Местоположение первого элемента каждой строки. Разреженный столбцовый формат. Матрица хранится в 3 одномерных массивах: A – Постолбцово слева на право; LI – Номера строк; LJ – Местоположение первого элемента каждого столбца. 15. Какая матрица называется разреженной структурно-симметричной? Если выполняется два условия: 1) Если Aij = 0, то и Aij = 0; 2) Если Aij != 0, то и Aij != 0; 16. Как хранятся структурно-симметричные разреженные матрицы? Такие матрицы хранятся в виде пяти одномерных массивов: - Массив для диагонали AD; - Массив элементов, стоящих над диагональю AU (по строкам, сверху вниз); - Массив элементов, стоящих под диагональю AL (по столбцам, слева направо); - Массив LJ – номера столбцов элементов, хранимых в матрице AU или строк, хранимых в матрице AL. - Массив LI – местоположение первого элемента каждой строки в AU или каждого столбца в AL. 17. Какая матрица называется ленточной? Матрица, все ненулевые элементы которой заключены внутри ленты, образованной диагоналями, параллельными главной. 18. Как хранятся разреженные ленточные матрицы? Ленточно-строчный формат: массив NxM, в котором построчно хранятся ненулевые элементы матрицы A. Побочные диагонали доопределены до размерности n нулями. Элементы на главной диагонали собираются в одну вертикаль, сдвигая остальные за собой, пустоты заполняются нулями. Ленточно-столбцовый формат: массив NxM, в котором по столбцам хранятся ненулевые элементы матрицы A. Побочные диагонали доопределены до размерности n нулями. Элементы на главной диагонали собираются в одну горизонталь, сдвигая остальные за собой, пустоты заполняются нулями. Диагональный формат: массив NxM. n–размерность массива матрицы, m–кол-во ненулевых диагоналей. Побочные диагонали доопределяются до общего нулями. Элементы на неплотно расположенных диагоналях – среди диагоналей с элементами есть нулевые, упакованная матрица плотная – нулевые диагонали убираются. 19. Какая структура называется неориентированным графом? В неориентированном графе отношения симметричны, т.е.: (u,v) = (v,u). В неориентированном графе нет дуг, связи называют ребрами. Граф, ребра которого не имеют направлений. 20. Какая структура называется ориентированным графом? В орграфе бинарные отношения между вершинами упорядочены. Такие отношения называют дугами. 21.Методы хранения графов (матрицы смежности, инцидентности, списки смежных вершин). Матрица смежности графа G с конечным числом вершин n — это квадратная матрица A размера n, в которой значение элемента Aij равно числу рёбер из i-й вершины графа в j-ю вершину. Матрица инцидентности — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро (дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам. Ненулевое значение в ячейке матрицы указывает связь между вершиной и ребром (их инцидентность). Каждая строка соответствует определенной вершине графа, а столбцы соответствуют связям графа. В ячейку, на пересечении i-ой строки j-ым столбцом матрицы записываются: 1 – в случае, если связь входит в вершину; -1 – если связь выходит из вершины; 0 – во всех остальных случаях (петля или нет инцидентности); Списки смежных вершин – список смежности для G=(V, E) с числом вершин V=N и записывается в виде одномерного массива длины N каждый, элементы которого представляют собой ссылку на список. 22. Какая структура называется деревом? Что такое корень, сын, лист, потомок и предок? Дерево – неориентированный граф без циклов. Корень – вершина дерева. Сын – элемент на следующем уровне от текущего; лист – элемент без потомков; потомок – элемент на любом уровне ниже текущего; предок – элемент на любом уровне выше текущего. 23. Методы хранения деревьев. Матрица смежности - аналогично графам Матрица инцидентности - аналогично графам Списки смежности: структура узла (содержит значение, количество сыновей и массив указателей-сыновей или λ в случае пустоты). Дерево, каждая вершина которого имеет не более двух сыновей. 25. Методы хранения бинарных деревьев. - Матрицы смежности; - Матрицы инцидентности; - Списки смежности; - Двумерные матрицы (столбцы: номер вершины, левый потомок, правый потомок); - Одномерные массивы (корню соответствует ячейка 1; если у узла в ячейке i есть потомки, то левый хранится в ячейке i*2, правый в i*2+1, иначе в эти ячейки помещается λ). 26. Какая функция называется рекурсивной? Функция, которая вызывает саму себя. Рекурсия разбивает программу на более мелкие подзадачи, которые могут быть решены с помощью этой же программы. 27. Прямая и косвенная рекурсия. Явная (прямая) рекурсия – такая программа (функция), которая содержит несколько вызовов этой же функции. Косвенная (не явная) рекурсия – одна функция вызывает другую функцию, а это в свою очередь прямо или косвенно приводит к вызову первоначальной функции. 28. Методика решения задачи с помощью рекурсивной функции. Если задача может быть разложена на подзадачи того же типа, но меньшей размерности, то анализ такой задачи включает 3 этапа: Параметризация – выделяют параметры, которые используются для описания условия задачи, а затем в решении. Поиск тривиального случая (база рекурсии) – определяем тривиальный случай, при котором решение очевидно, то есть не требует обращение функции к себе. Декомпозиция – выражают общий случай через более простые подзадачи с измененными параметрами. Стек вызовов — стек, хранящий информацию для возврата управления из функций в программу или подпрограмму (при вложенных или рекурсивных вызовах). При вызове подпрограммы в стек заносится адрес возврата — адрес в памяти следующей инструкции приостанавливаемой программы, а управление передается подпрограмме. При последующем вложенном или рекурсивном вызове в стек заносится очередной адрес возврата и так далее. При возврате из подпрограммы адрес возврата снимается со стека, и управление передается на следующую инструкцию приостановленной программы (или подпрограммы). 30. Хвостовая рекурсия. Специальный случай рекурсии, при котором рекурсивный вызов функции самой себя является ее последней операцией. 31. Алгоритм прохождения (обхода) деревьев в глубину. Стратегия этого поиска состоит в том, чтобы идти вглубь одного поддерева настолько, насколько это возможно. Прямой порядок: от корня до листьев. Обратный порядок: от листьев до корня. 32. Алгоритм прохождения (обхода) деревьев в ширину. В начале развертывается корневой узел, затем преемники корня, затем преемники этих преемников и т.д. 33. Двунаправленный поиск. Двунаправленный поиск пути в ширину — усложненный алгоритм поиска в ширину, идея которого заключается в формировании процесса поиска от начальной и от конечной вершины графа. 34. Алгоритм AI-поиска. - Начальное состояние, из которого AI-программа приступает к работе.; - Описание возможных действий, доступных AI-программе, которые переводят задачу из одного состояния в другое.; - Проверка цели - позволяющая определить, является ли данное конкретное состояние целевым состоянием; - Функция стоимости пути, которая назначает числовое значение стоимости каждому пути. 35. Рекурсия и задачи удовлетворения ограничениям. 36. Рекурсия и решение головоломок. 37. Рекурсия и игры двух игроков. 38. Дерево решений для игр двух игроков. 39.Стратегия минимакса. Минимакс — правило принятия решений для минимизации возможных потерь из тех, которые нельзя предотвратить при развитии событий по наихудшему для него сценарию. Основной принцип – контролировать ситуацию так, чтобы некоторые эффекты были минимизированы, а другие максимизированы. У нас есть функция для оценки хода человека/компьютера. Максимальное значение этой функции - выигрышный шаг компьютера, минимальное - выигрышный шаг человека. Так как нам надо выиграть за компьютер то мы будет выбирать для себя лучший ход по MAX оценке. 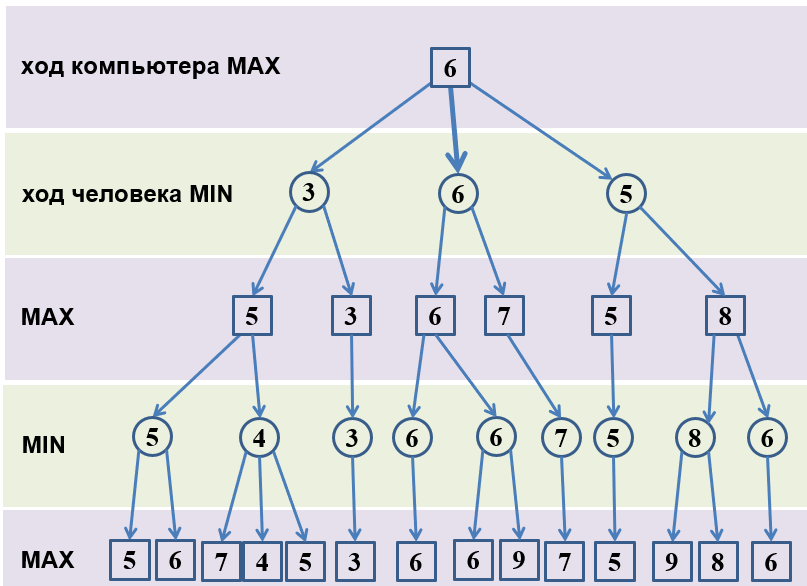 40. Альфа-Бета отсечение. 41.Последовательный поиск. Последовательный перебор элементов, где на каждом шаге мы сравниваем элемент с искомым. Сложность алгоритма: O(n). 42. Логарифмический поиск. Поиск методом деления пополам, беря середин. Сложность алгоритма: O (log2 n). 43.Какие таблицы называются статическими, динамическими? Статистические таблицы – таблицы, в которых включение и исключение записей происходит настолько редко, что потерями времени на них можно пренебречь и перестроить таблицу заново. Динамические таблицы – таблицы, в которых происходит включение и исключение имён. 44.Задача построения оптимального дерева в общем виде. Чтобы поиск выполнялся быстрее, требуется расположить тяжелые или наиболее часто используемые ключи ближе к корню. 45. Какой алгоритм называется эвристическим? Эвристический алгоритм – алгоритм, имеющий следующие свойства: - Он находит хорошее, но не обязательно оптимальное решение. - Его быстрее и проще реализовать, чем любой известный точный алгоритм, т.е. алгоритм гарантирующий нахождение оптимального решения. - Он требует меньше вычислительных ресурсов и работает, как правило, гораздо быстрее. 46. Эвристики построения оптимальных деревьев. Эвристика №1: К построенному дереву добавляем очередной узел таким образом, чтобы его левые и правые поддеревья имели максимально близкое количество вершин, считая листья. Эвристика №2: К построенному дереву добавляем очередной узел таким образом, чтобы его левые и правые поддеревья имели максимально близкие суммы весов или суммы частот обращения к вершинам. Эвристика №3: Самые тяжелые ключи помещаем ближе к корню. 47. AVL-Деревья. АВЛ-дерево — сбалансированное по высоте двоичное дерево поиска: для каждой его вершины высота её двух поддеревьев различается не более чем на 1. 48. Что такое балансировка и когда она применяется. После выполнения многочисленных включений и исключений дерево бинарного поиска становится значительно асимметричным, поэтому после каждой операции, изменяющее дерево, необходимо выполнять операцию балансировки. Всегда желательно, чтобы все пути в дереве от корня до листьев имели примерно одинаковую длину. В противном случае теряется производительность. 49. Операции вращения и двойного вращения, когда применяются? Если дерево и соответствующее поддерево перекошены в одну сторону применяется операция вращения. Для балансировки дерева применяется операция "поворот дерева". Если дерево и соответствующее поддерево перекошены в разные стороны применяется операция двойного вращения. 50. Какая структура называется B-деревом, когда применяются? В-дерево порядка M - это дерево, которое либо пусто, либо состоит из K узлов с K−1 ключами и K связями с деревьями, представляющими каждый из K ограниченных ключами интервалов  Структура B-дерева применяется для организации индексов во многих современных СУБД. B-дерево может применяться для структурирования (индексирования) информации на жёстком диске (как правило, метаданных). 51. Какая структура называется DB деревом, когда применяются? 2-3 дерево — структура данных, представляющая собой сбалансированное дерево поиска, такое что из каждого узла может выходить две или три ветви и глубина всех листьев одинакова. 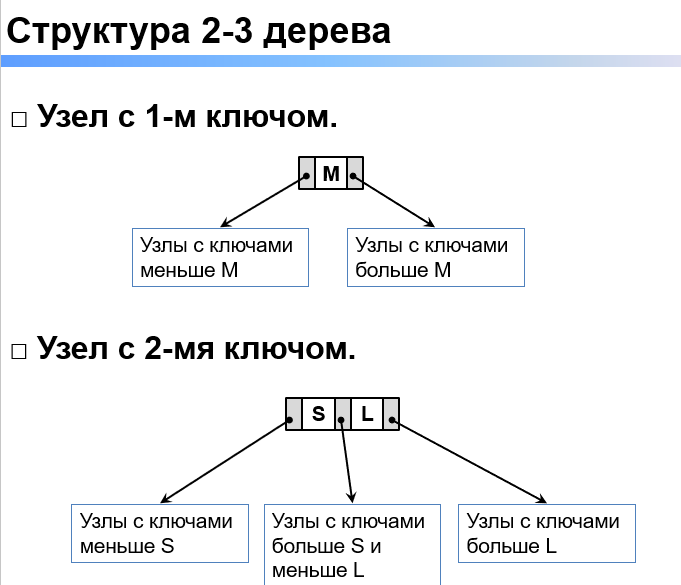 Применяются, когда мало памяти на диске, экономя ее. 52. Какая структура называется 2-3-4 деревом, когда применяются? 2-3-4 дерево похоже на 2-3 дерево, но может содержать четырехместные узлы, т.е. узлы, имеющие четыре дочерних узла и три элемента данных. Применяются для большего количества данных. 53. Что такое многомерный поиск. Стратегии двумерного поиска. В задаче многомерного поиска, каждый ключ – р-вектор из двух или более компонент р=(р1…рn). В общем случае, задача многомерного поиска решается путём объединения из K компонент, одной единственной компоненты, и далее решается задача одномерного поиска. Другими словами, вы стремитесь найти значение на пересечении определенной строки и столбца. Это называется матричным поиском (также известным как двумерный или поиск в диапазоне). 54. На чем основан цифровой и лексикографический поиск Лексикография – разбор ключей по символам. Цифровой поиск – посимвольное рассмотрение слева направо каждого ключа Х (поиск подстроки в строке). 55. Какая структура называется бором? Свойства боров Бор — это дерево, в котором каждая вершина обозначает какую-то строку. На ребрах между вершинами написана 1 буква. Таким образом, каждой вершине соответствует ровно одна строка. 1) Быстрый поиск, особенно в случае <неуспеха>. 2) Неэффективное использование памяти, особенно для вершин далеких от корня. 3) Для любого множества имён существует ровно одно дерево цифрового поиска, а значит всего одна таблица – бор. Это исключает вопрос о построении оптимального дерева поиска. 4) Алгоритмы поиска, включения, исключения просты 56. Что такое хеширование? Хеширование – вычисление адреса (хэша) с помощью хэш-функции в пространстве адресов A для каждого имени из пространства имён S (ключа). 57. Свойства хеш-функции? 1. Функция не должна выходить за пределы пространства адресов. 2. Функция должна быть вычислима для любого ключа. 1) Отображать пространство имён в пространство адресов. 2) По возможности использовать все биты или символы ключа. 3) Любая хэш-функция должна быть оттестирована на контрольных примерах. 58. Минимально идеальная хэш-функция Минимально идеальная хеш-функция преобразует ключи в адреса без коллизий (1 ключ соответствует лишь 1 уникальному значению). 59. Хеш-функция деления Хеш-функция деления: h(k) = k % m, где k – ключ, m – размер хеш-таблицы. 60. Хеш-функция умножения Умножение ключа на константу C [0 до 1] и умножение на K [размер таблицы] 61. Хеш-функция “середины квадрата” Возведение ключа в квадрат и взятие из середины квадрата m битов 62. Хеш-функция преобразования системы счисления. Хеш-функция преобразования системы счисления: ключ-число, заданный в системе счисления q, представляют, как заданный в системе счисления p, переводят в десятичную систему счисления, берут остаток от деления на размер таблицы. 63. Хеш-функция деления многочленов 64. Хеш-функция свертки (слияния). Ключ - сумма частей, каждая из которых имеет длину, равную длине требуемого адреса. После сложения отсекаются старшие разряды 65. Хеш-функция для строковых ключей Сумма выражения ниже: Для каждого символа мы берем его ASCII и умножаем на 128 в степени ( длина слова - позиция) 66. Оценка качества хеш-функции. Количество коллизий на области таблицы. 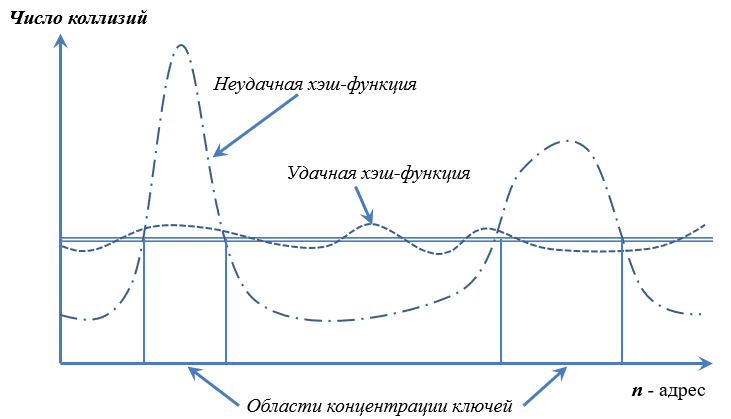 67. Что такое коллизия. Стратегии их разрешения? Коллизия – возвращение одинакового результата для 2-х разных ключей. Стратегии: Методы открытой адресации (статические) – линейная схема, случайная схема, квадратичная схема, двойное хеширование, рехеширование; Методы преодоления коллизий в динамических структурах – внутренние и внешние цепочки, бинарные деревья. 68. Линейная схема разрешения коллизий При добавлении нового ключа всегда можно определить, занята ли данная ячейка таблицы или нет. Если да, алгоритм осуществляет перебор по кругу, пока не встретится «открытый адрес» (свободное место). 69. Случайная схема разрешения коллизий Если место куда мы вставляем ключ уже занято, то мы идем с шагом C вправо и вставляем в свободное место. 70. Квадратичная схема разрешения коллизий Похожа на линейную, но шаг перебора зависит от номера попытки найти свободный элемент в квадрате. 71. Двойное хеширование Это использование двух хэш-функций для нахождения позиции элементу (в случае если его место от первой хэш-функции занято). 72. Рехеширование хэш-таблиц Увеличение размера таблицы. Из-за этого мы меняем хэш-функцию и с помощью этой хэш-функции переразмещаем элементы в новой таблице. 73. Преодоления коллизий с помощью динамических структур Хэш-таблица состоит из списков, где ключи с одинаковым хэшем добавляются в список[хэш]. При коллизиях элемент помещается в список или дерево и никак не влияет на время поиска других элементов. 74. Основные методы сортировки Сортировка пузырьком Сортировка выбором Сортировка вставками быстрая сортировка сортировка Шелла пирамидальная сортировка сортировка слиянием сортировка с помощью бинарного дерева. Целью сортировки является облегчить последующий поиск элементов в отсортированном множестве. 76. Быстрая сортировка. Алгоритм состоит из трех шагов: Выбрать элемент из массива. Разбиение: перераспределение элементов в массиве таким образом, что элементы, меньшие опорного, помещаются перед ним, а большие или равные - после. Рекурсивно применить первые два шага к двум подмассивам слева и справа от опорного элемента. 78. Поразрядная сортировка. Предназначена для сортировки целых чисел, записанных цифрами. Но так как в памяти компьютеров любая информация записывается целыми числами, алгоритм пригоден для сортировки любых объектов, запись которых можно поделить на «разряды», содержащие сравнимые значения. 79. Сортировка методом простого слияния. Для решения задачи сортировки эти три этапа выглядят так: Сортируемый массив разбивается на две части примерно одинакового размера; Каждая из получившихся частей сортируется отдельно, например — тем же самым алгоритмом; Два упорядоченных массива половинного размера соединяются в один. Кванти́ль в математической статистике — значение, которое заданная случайная величина не превышает с фиксированной вероятностью. 81. Стратегии частичной сортировки. Полная сортировка - это возврат списка элементов, в котором все элементы отображаются по порядку. В то время как частичная сортировка возвращает список из k наименьших (или k наибольших) элементов по порядку. Другие элементы (выше k наименьших) также могут быть отсортированы, как при частичной сортировке по месту, или могут быть отброшены, что является обычным при потоковой частичной сортировке. Обычным практическим примером частичной сортировки является вычисление «100 лучших» некоторого списка. Намного быстрее в использовании для больших списков в сравнении с сортировкой вставки и пузырьковой сортировки, потому что он не проходит через весь список несколько раз; Стабильное время выполнения; Можно использовать для больших файлов; Идеально для организации труднодоступных данных. |
