РЕШЕНИЯ МЕТОДИЧКИ ЧАСТЬ 6 BETA. 1 Электрическое поле совершило работу

• Название: 1 Электрическое поле совершило работу
• Дата: 11.12.2021
• Размер: 0.96 Mb.
• Имя файла: РЕШЕНИЯ МЕТОДИЧКИ ЧАСТЬ 6 BETA.doc
• Тип: Документы; #300063
• страница: 1 из 2

1-1. Микрочастица с массой т и зарядом ускорена разностью потен­циалов из состояния покоя. Найти длину волны де Бройля этой микро­частицы (в пм). .

1-2. Электрическое поле совершило работу А над покоившейся микро­частицей с массой т. Найти длину волны де Бройля ускоренной микро-частицы. .

1-3. Электрическое поле совершило работу А над покоившейся микро­частицей с массой т, при этом длина волны де Бройля микрочастицы ста­ла равна 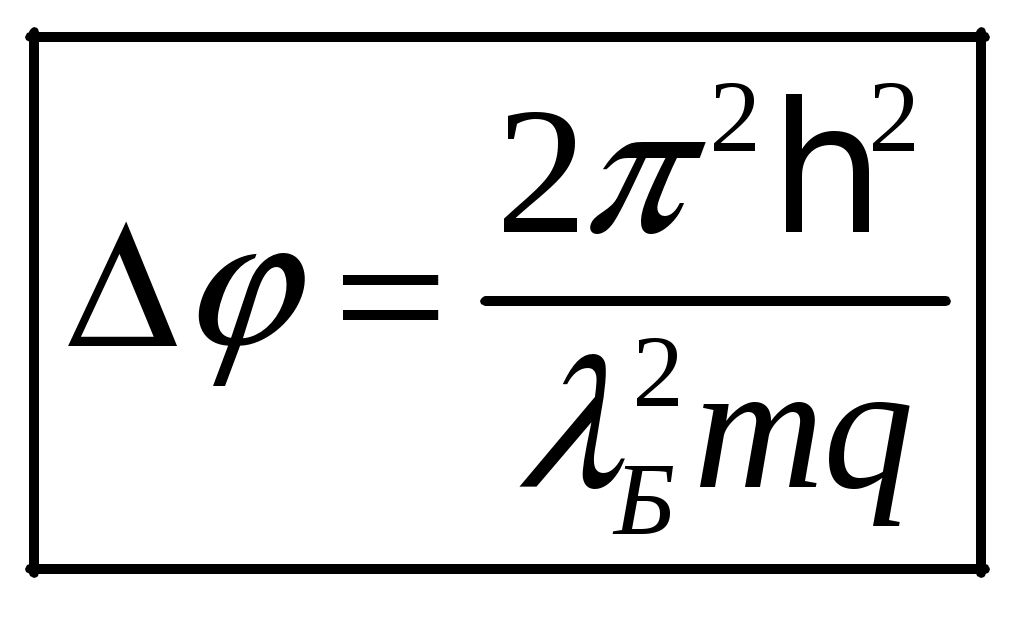. Найти работу поля А (в эВ). .

1-4. Электрон находится на третьей боровской орбите атома, радиус которой .

а) Найти длину волны де Бройля этого электрона (в нм).

б) Чему станет равна длина волны де Бройля этого электрона (в нм) на четвертой боровской орбите? .

в) Чему равна скорость этого электрона (в км/с)?

г) Чему равен импульс этого электрона?

д) Чему станет равен импульс этого электрона при переходе на 4-ю орбиту?

е) Чему станет равна скорость этого электрона (в км/с) при переходе на 4-ю орбиту?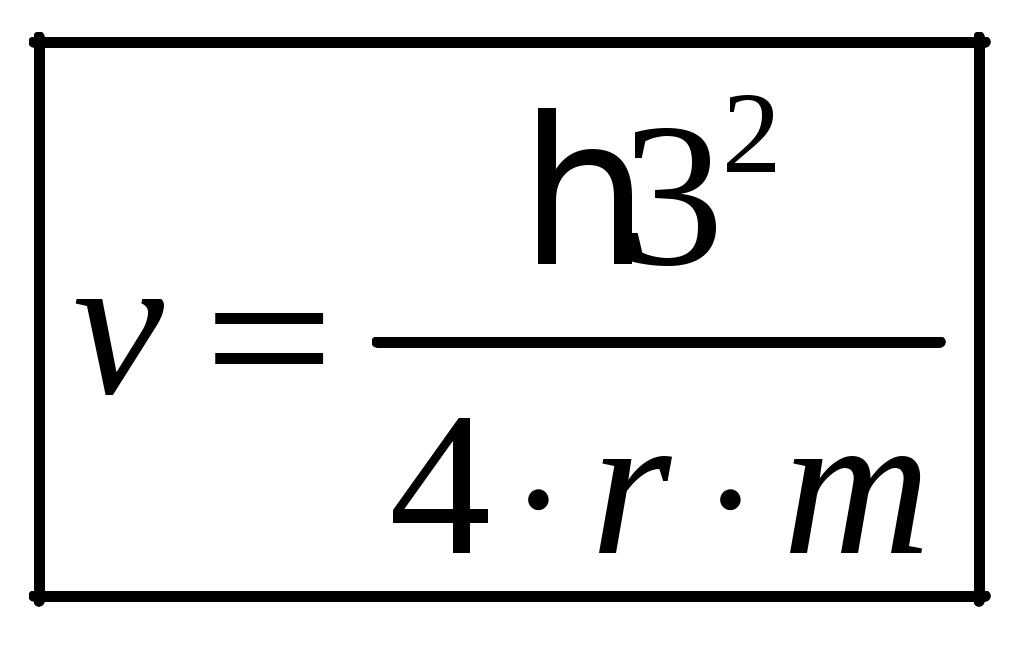

ж) Чему станет равна кинетическая энергия этого электрона (в эВ) при переходе на 4-ю орбиту?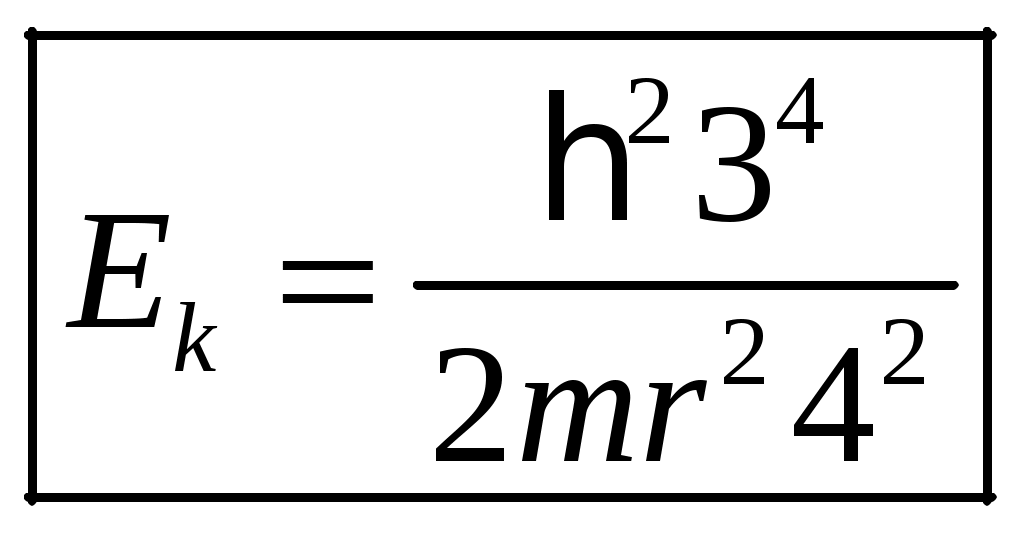

1-5. Электрон находится на третьей боровской орбите атома, радиус которой нм.

а) Во сколько раз увеличится момент импульса этого электрона при пере­ходе на четвертую орбиту?

б) На сколько электрон-вольт уменьшится кинетическая энергия этого электрона при переходе на четвертую орбиту?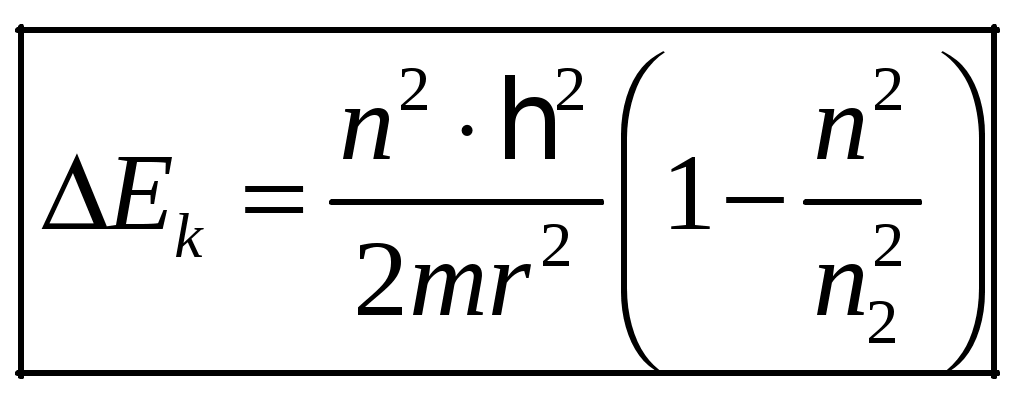

в) На сколько нанометров увеличится длина волны де Бройля этого элек­трона при переходе на четвертую орбиту?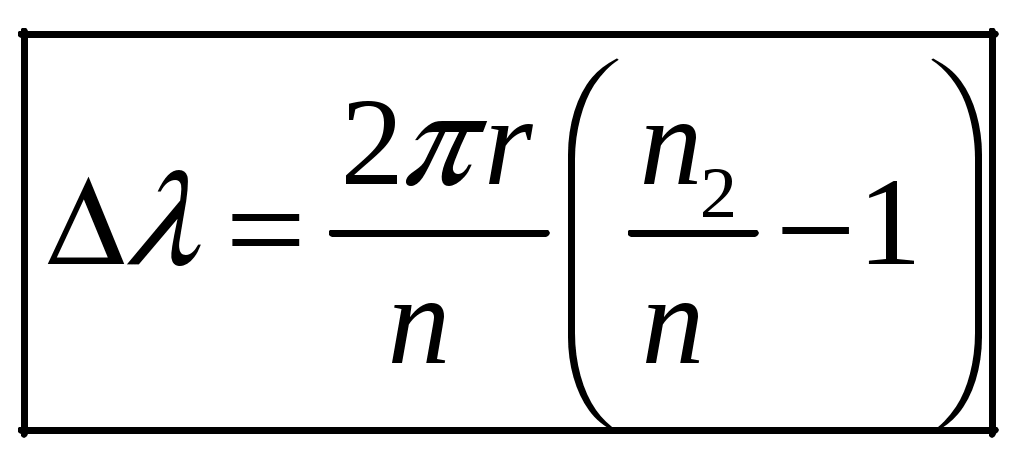

г) На сколько увеличится момент импульса этого электрона при переходе на четвертую орбиту?

д) Во сколько раз уменьшится кинетическая энергия этого электрона при переходе на четвертую орбиту?

е) Во сколько раз уменьшится импульс этого электрона при переходе на четвертую орбиту? .

2-1. 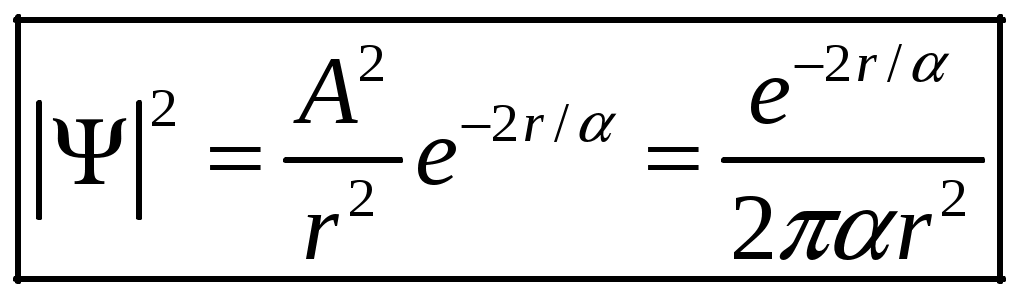-функция некоторой частицы имеет вид , где -расстояние от этой частицы до силового центра. Определить плотность вероятности нахождения этой частицы на расстоянии от начала координат. .

2-2. -функция некоторой частицы имеет вид , где - рас­стояние от этой частицы до силового центра;

а) На каком удалении 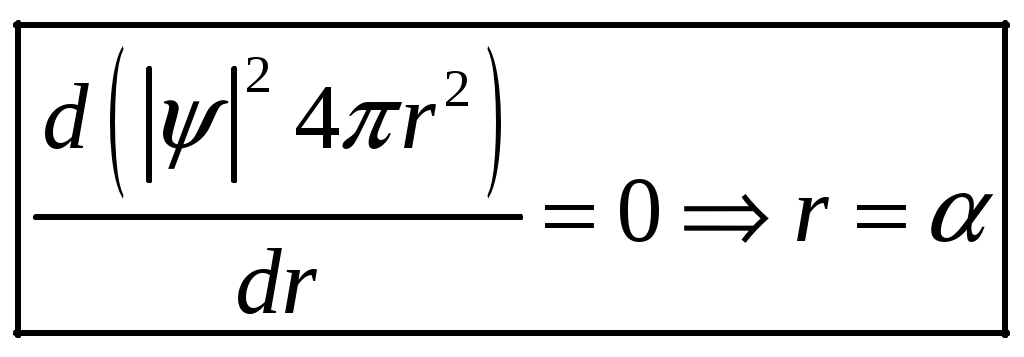от начала координат (в нм) вероятность нахожде­ния микрочастицы максимальна? .

б) Определить плотность вероятности нахождения этой частицы на расстоянии г от начала координат.

2-3. -функция некоторой частицы имеет вид , где а - ширина ямы. Используя условие нормировки, определите коэффициент . .

2-4. Микрочастица в одномерной прямоугольной потенциальной яме с бесконечными стенками имеет волновую функцию . Найти ширину ямы а. .

2-5. Волновая функция микрочастицы с массой m имеет вид 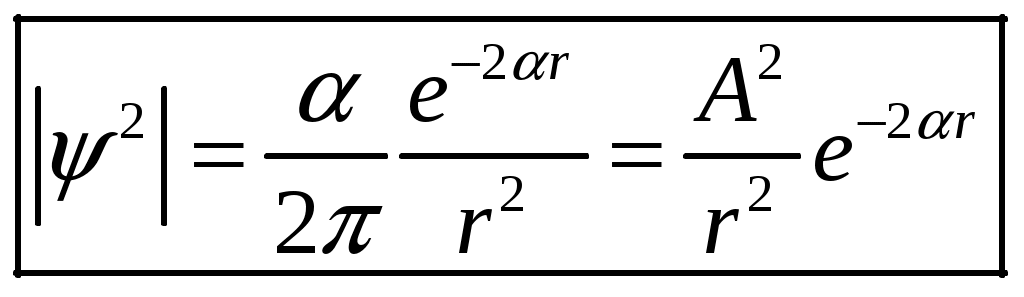, где - расстояние от этой частицы до силового центра; некоторая постоянная . Определить плотность вероятности нахождения этой частицы на расстоянии от начала координат.

2-6. Найти максимальную плотность вероятности нахождения микро­частицы в одномерной прямоугольной потенциальной яме шириной с бесконечными стенками, если волновая функция имеет вид . РЕШЕНИЕ. Возвести в квадрат. Найти от этого производную по и приравнять ее нулю. Из уравнения найти .Подставить этот в .

2-7. Найти координату микрочастицы в одномерной прямоугольной потенциальной яме шириной с бесконечными стенками, при ко­торой плотность вероятности ее нахождения максимальна. Волновая функция микрочастицы имеет вид . РЕШЕНИЕ. Возвести в квадрат. Найти от этого производную по и приравнять ее нулю. Из уравнения найти .

2-8. Волновая функция микрочастицы определена только в области , - ширина ямы.

.

А) Найти минимальное расстояние между точками, в которых вероят­ность обнаружения частицы максимальна.

Б) Найти максимальное расстояние между точками, в которых вероят­ность обнаружения частицы максимальна.

2-9. Свободная микрочастица имеет сферически симметричную волновую функцию 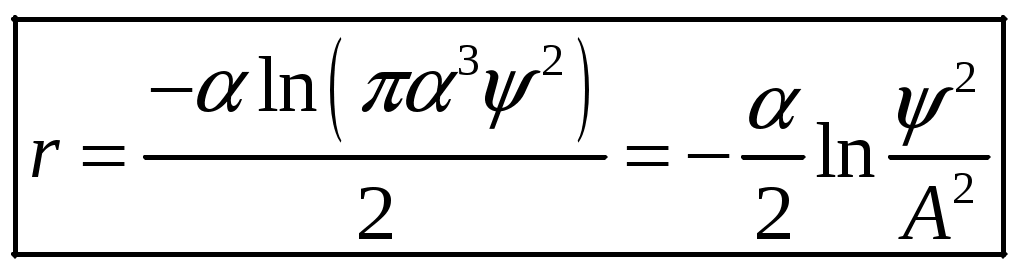, где . Определить расстояние от частицы до силового центра (в нм), где плотность вероятно­сти нахождения микрочастицы равна . .

2-10. Волновая функция, описывающая состояние электрона в одно­мерной прямоугольной потенциальной яме с бесконечно высокими стен­ками имеет вид 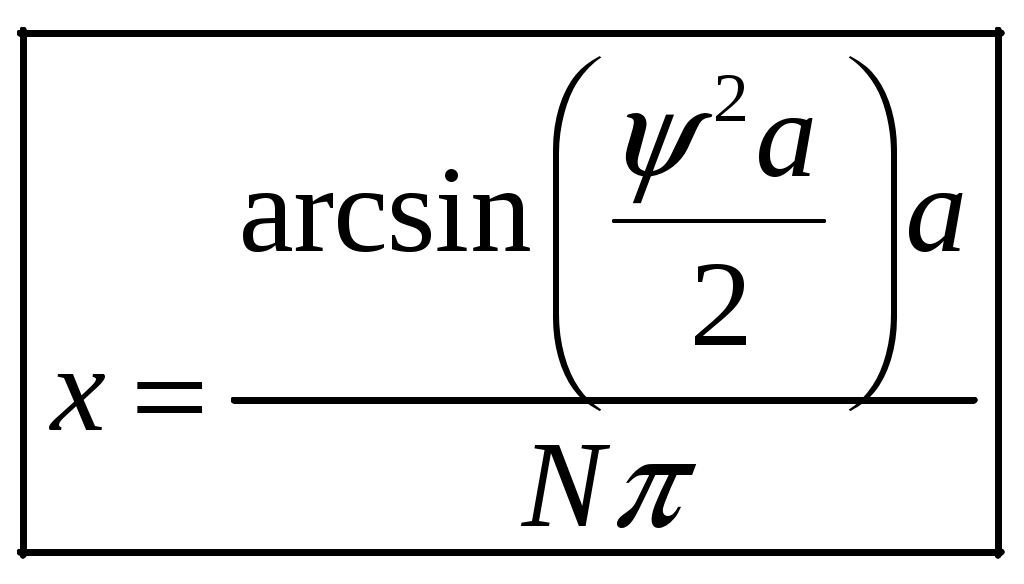. Определить координату электрона (в нм), где плотность вероятности его нахождения равна . . ВНИМАНИЕ!!! Арксинус считать в радианах (Rad).

3-1. Волновая функция микрочастицы с массой т имеет вид . Найти полную энергию частицы (в эВ), считая потенциальную энергию равной нулю. .

3-2. Волновая функция микрочастицы с массой т имеет вид: . Найти полную энергию частицы (в эВ), считая по­тенциальную энергию равной нулю. .

3-3. Волновая функция микрочастицы с массой 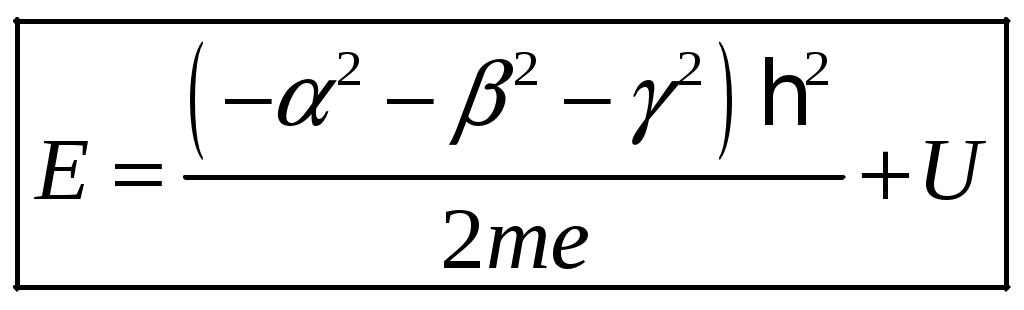имеет вид . Найти полную энергию частицы (в эВ), считая потенци­альную энергию равной . .

3-4. Волновая функция микрочастицы с массой т имеет вид а) 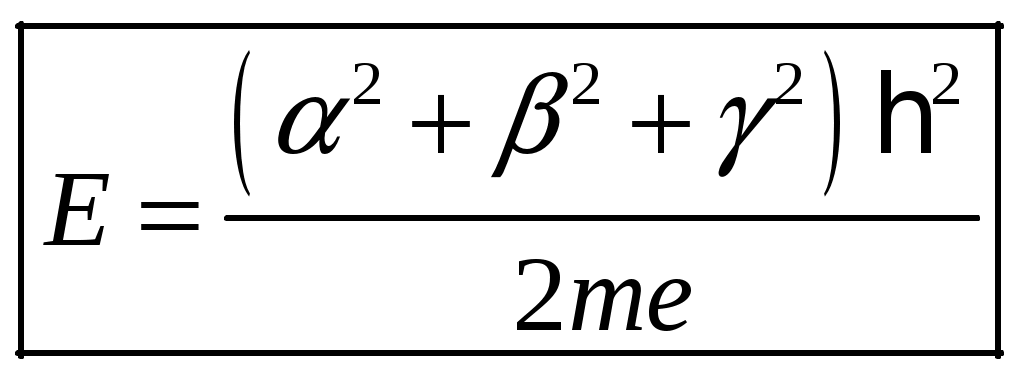; б) г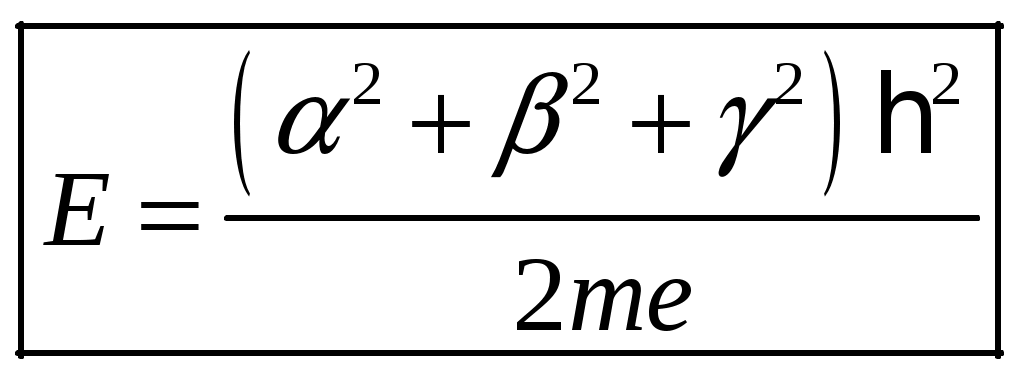де i – мнимая единица. Найти полную энергию частицы (в эВ), считая потенциальную энергию равной нулю. а) ; б) .

3-5. Волновая функция микрочастицы с массой т имеет вид 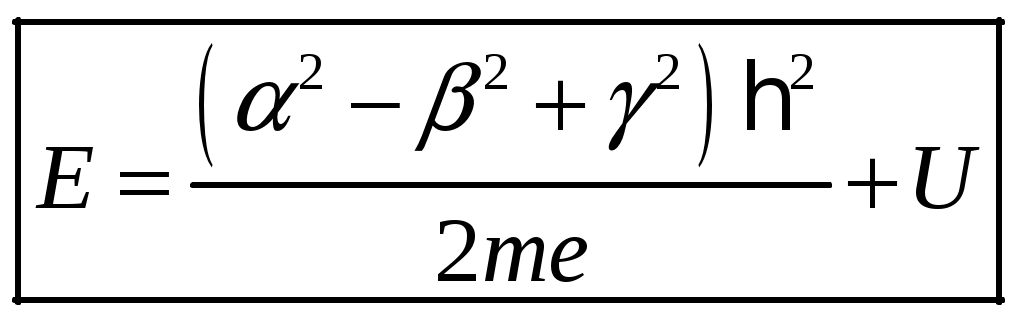, где i- мнимая единица. Найти полную энергию частицы (в эВ), считая потенциальную энергию равной . .

3-6. Волновая функция микрочастицы с массой т имеет вид 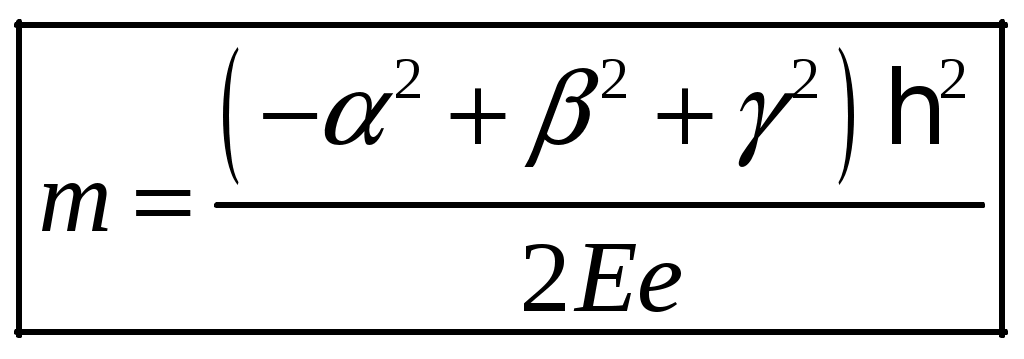. Кинетическая энергия частицы равна Е. Найти массу частицы. .

3-7. Волновая функция микрочастицы с массой т имеет вид , где i - мнимая единица. Кинетическая энергия части­цы равна Е. Найти массу частицы. .

3-8. Волновая функция микрочастицы с массой т имеет вид 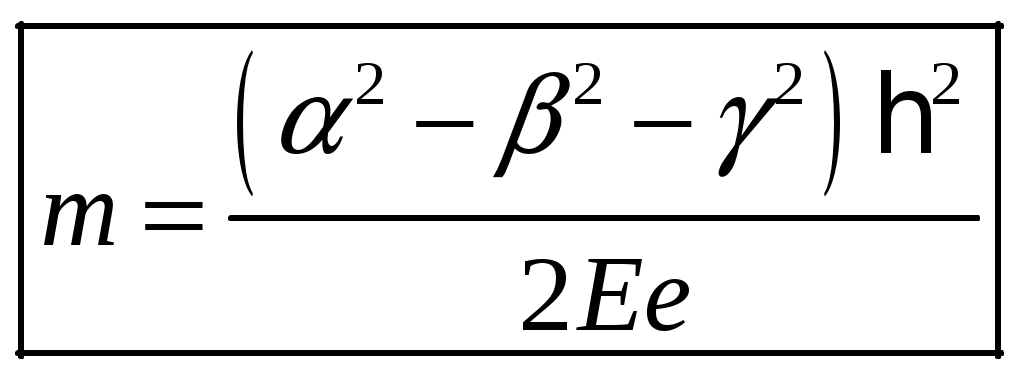. Кинетическая энергия частицы равна Е. Найти массу частицы. .

3-9. Волновая функция микрочастицы с массой т имеет вид:

а) 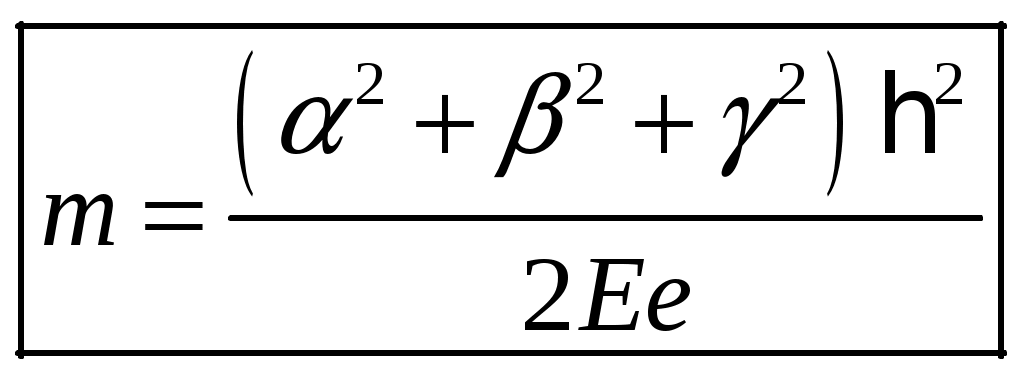; б) , где i - мнимая единица. Кинетическая энергия частицы равна Е. Найти массу частицы. .

3-10. Волновая функция микрочастицы с массой т имеет вид 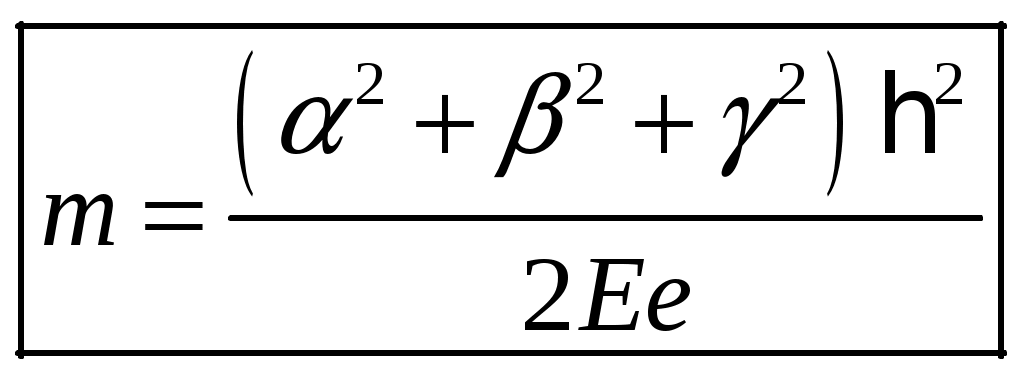, где i- мнимая единица. Кинетическая энер­гия частицы равна Е. Найти массу частицы. .

3-11. Волновая функция микрочастицы с массой т имеет вид . Кинетическая энергия частицы равна Е. Найти константу . .
3-12. Волновая функция микрочастицы с массой т имеет вид 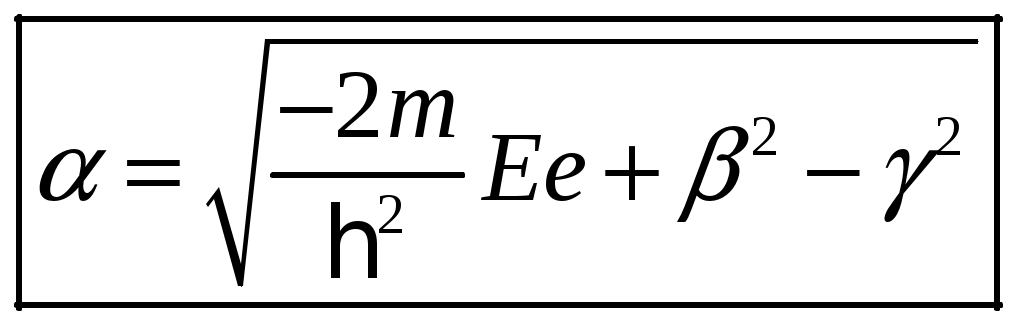, где i- мнимая единица. Кинетическая энергия частицы равна Е. Найти константу . .

3-13. Волновая функция микрочастицы с массой т имеет вид 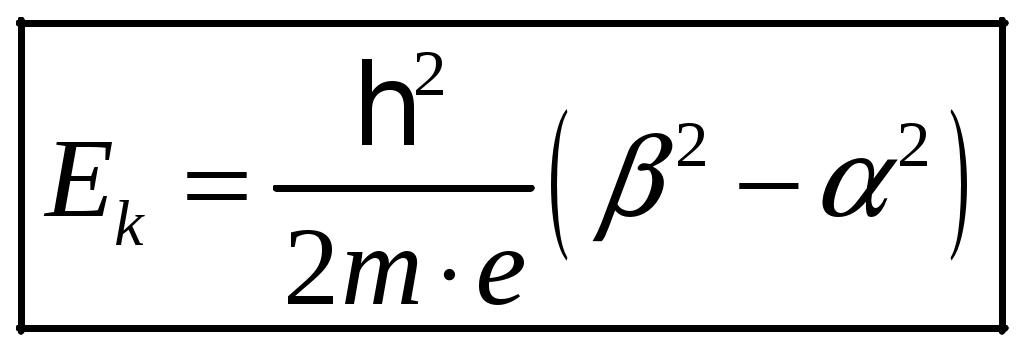,где i- мнимая единица. Найти кинетическую энергию частицы (в эВ). .

3-14. Волновая функция микрочастицы с массой т имеет вид , где i- мнимая единица. Кинетическая энергия части­цы равна Е. Найти массу частицы. .

3-15. Волновая функция микрочастицы с массой т имеет вид 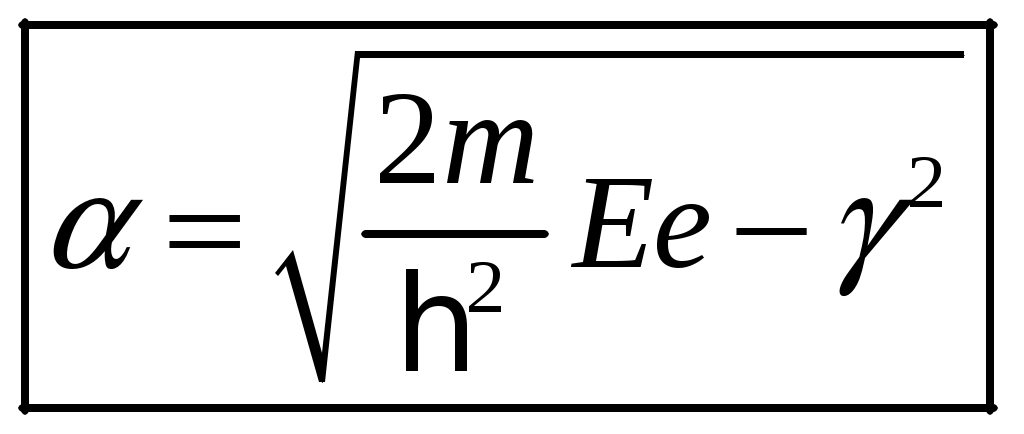, где i - мнимая единица. Кинетическая энергия части­цы равна Е. Найти константу . .

3-16. Волновая функция микрочастицы с массой т имеет вид . Кинетическая энергия частицы равна Е.

а) Найти кинетическую энергию частицы (в эВ). .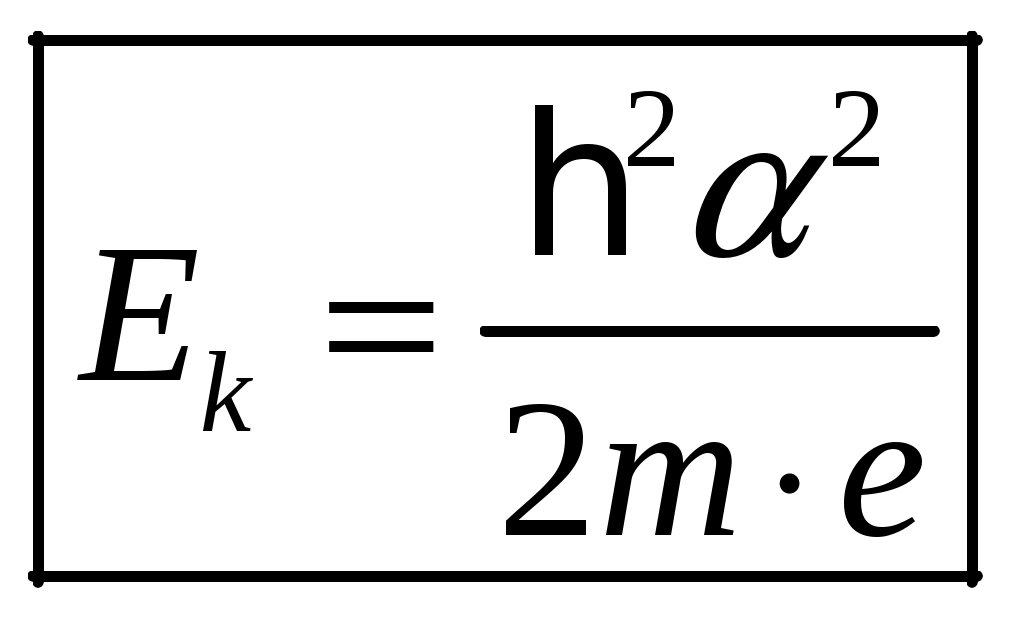

б) Найти массу частицы. .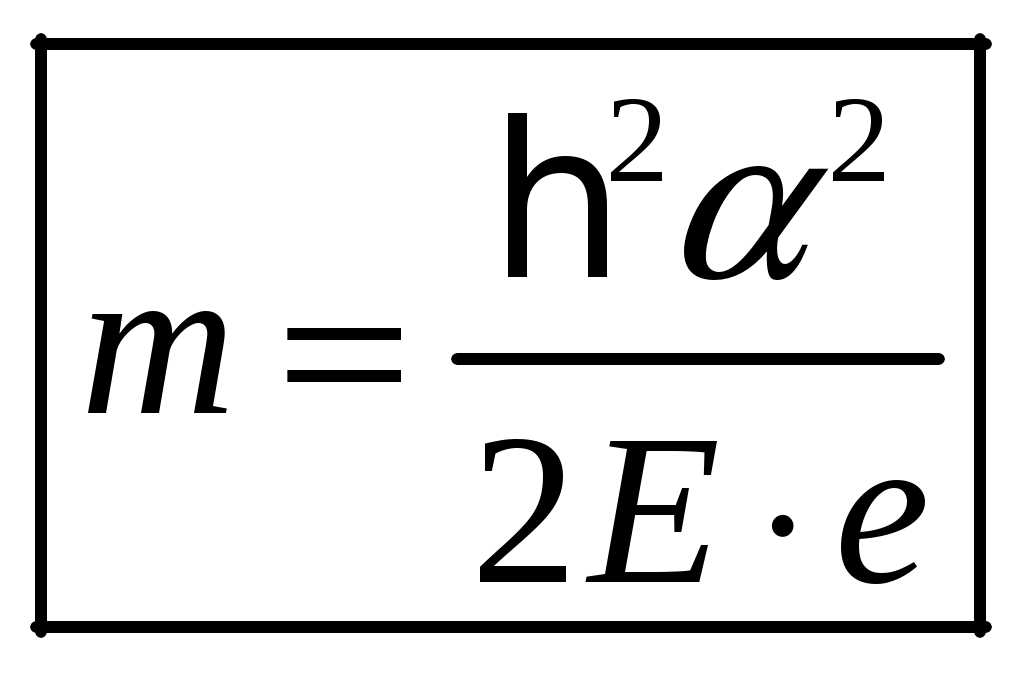

в) Найти константу . .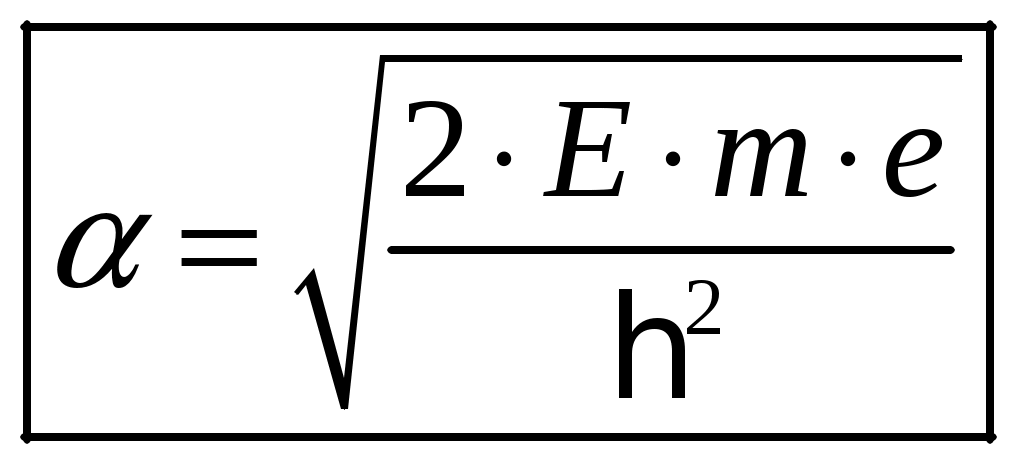

3-17. Волновая функция микрочастицы с массой т имеет вид , где i - мнимая единица. Найти кинетическую энер­гию частицы (в эВ). .

3-18. Волновая функция микрочастицы с массой т имеет вид , где i - мнимая единица. Кинетическая энергия час­тицы равна Е. Найти массу частицы. .

4-1. Микрочастица с массой т находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками шириной а.

а) Энергия микрочастицы на втором возбужденном уровне равна . ( )

б) Энергия микрочастицы на третьем возбужденном уровне равна . ( )

в) Энергия микрочастицы на третьем уровне равна . ( )

г) Энергия микрочастицы на четвертом уровне равна . ( )



А) Найти энергию излученного фотона (в эВ) при переходе микрочастицы в основное состояние. .

Б) Найти длину волны излученного фотона (в нм) при переходе микрочас­тицы в основное состояние. .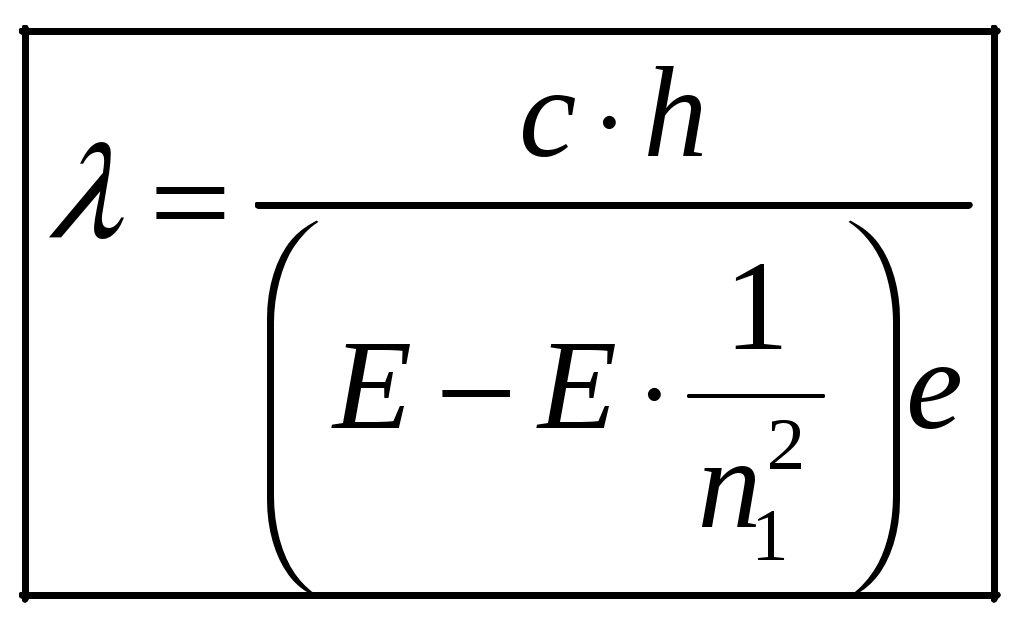

В) Найти импульс излученного фотона при переходе микрочастицы в ос­новное состояние. .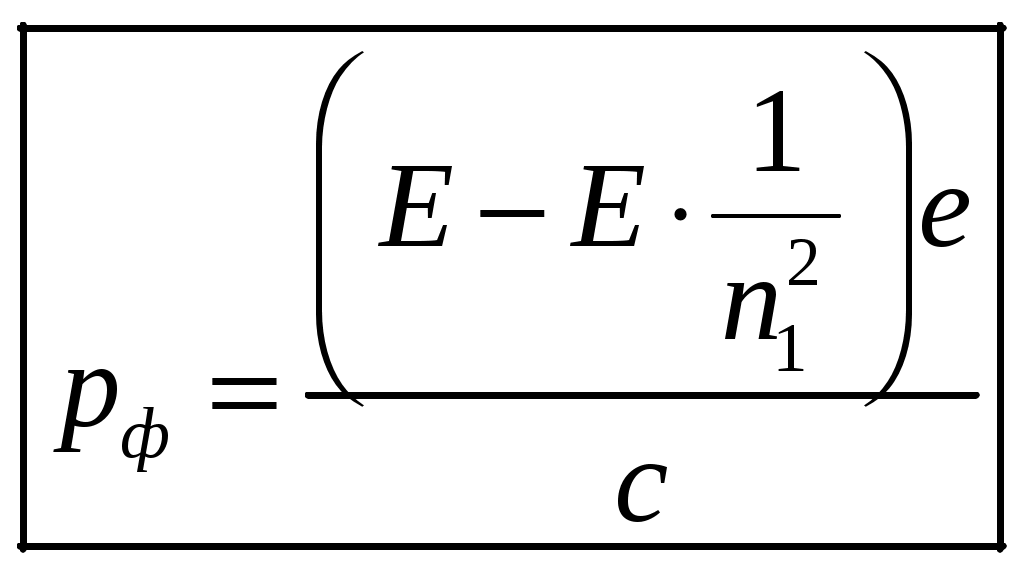

4-2. Микрочастица с массой т находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками шириной а. Находясь в основном состоянии, микрочастица поглотила фотон с энерги­ей и перешла:

а) во второе возбужденное состояние ( )

б) в третье возбужденное состояние ( )

в) на третий энергетический уровень ( )

г) на четвертый энергетический уровень ( ).

Затем эта частица совершила один переход в одно из состояний с меньшей энергией.

A) Найти наименьшую энергию фотона (в эВ), который может быть излу­чен этой частицей при таком переходе. .

Б) Найти наименьший импульс фотона, который может быть излучен этой частицей при таком переходе. .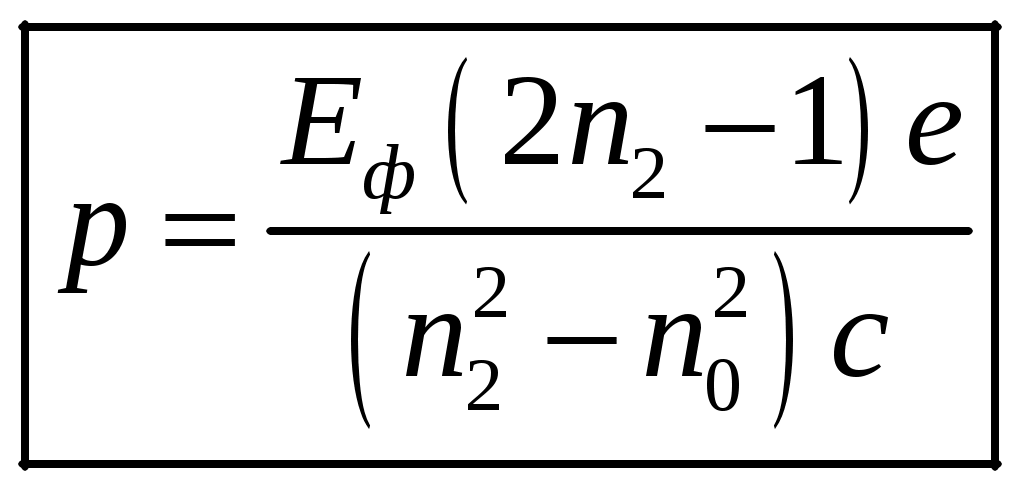

B) Найти наибольшую длину волны фотона (в нм). который может быть излучен этой частицей при таком переходе. .

4-3. Находясь в основном состоянии, одномерный квантовый гармони­ческий осциллятор поглотил фотон с энергией и оказался:

а) во втором возбужденном состоянии ( )

б) в третьем возбужденном состоянии ( )

Найти наибольшую длину волны фотона (в нм), который может быть из­лучен этим осциллятором. 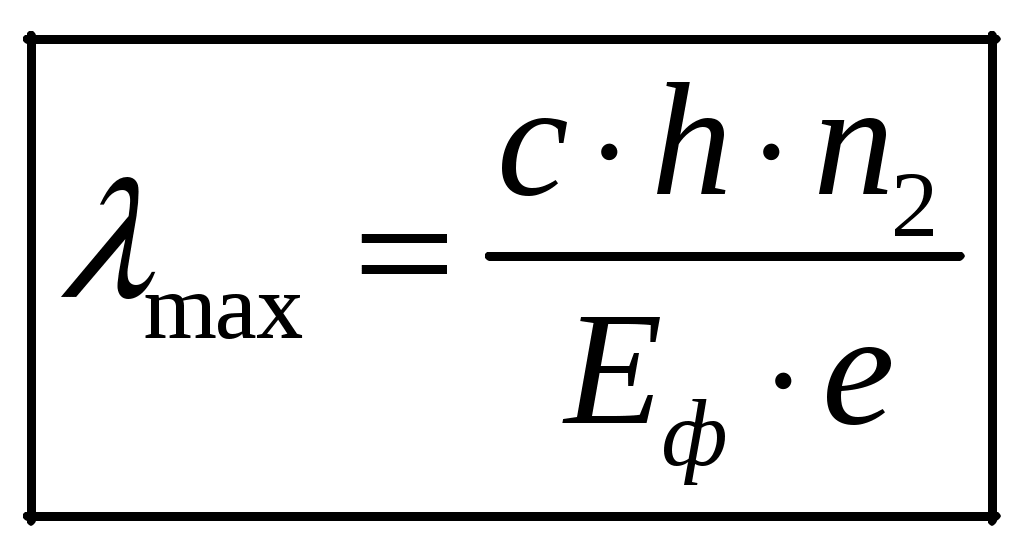. ВНИМАНИЕ!!! Здесь .

4-4. При переходе одномерного квантового гармонического осцилля­тора из четвертого возбужденного состояния в основное был излучен фо­тон с энергией Е. Найти:

а) длину волны фотона (в нм), который был бы излучен при переходе на соседний энергетический уровень. .

б) частоту фотона, который был бы излучен при переходе на соседний энергетический уровень.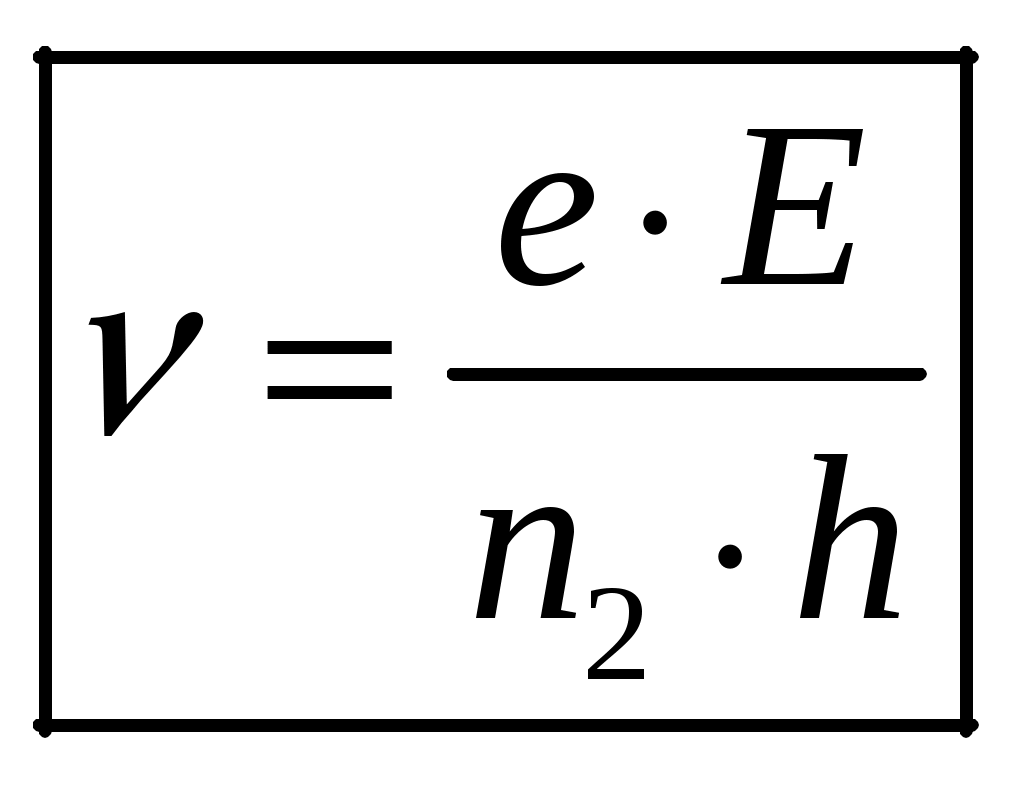

в) частоту фотона, который был излучен при последующем переходе в ос­новное состояние. .

4-5. При переходе одномерного квантового гармонического осцилля­тора из четвертого возбужденного состояния на соседний энергетический уровень был излучен фотон с энергией Е. Найти длину волны фо­тона (в нм), который был излучен при последующем переходе в основное состояние. , , .

4-6. Находясь в первом возбужденном состоянии, одномерный кванто­вый гармонический осциллятор поглотил фотон с энергией Е и оказался в третьем возбужденном состоянии. Найти:

а) наибольшую длину волны фотона (в нм), который может быть излучен этим осциллятором. ( ). .

б) наименьшую длину волны фотона (в нм), который может быть излучен осциллятором в этом состоянии. ( ). .

в) наименьшую частоту фотона, который может быть излучен этим ос­циллятором. ( ).

г) наибольшую частоту фотона, который может быть излучен осциллято­ром в этом состоянии. ( ). .

4-7. Находясь в основном состоянии, одномерный квантовый гармони­ческий осциллятор поглотил фотон с энергией Е и оказался во вто­ром возбужденном состоянии. Найти наименьшую частоту фотона, кото­рый может быть излучен этим осциллятором. ( ). .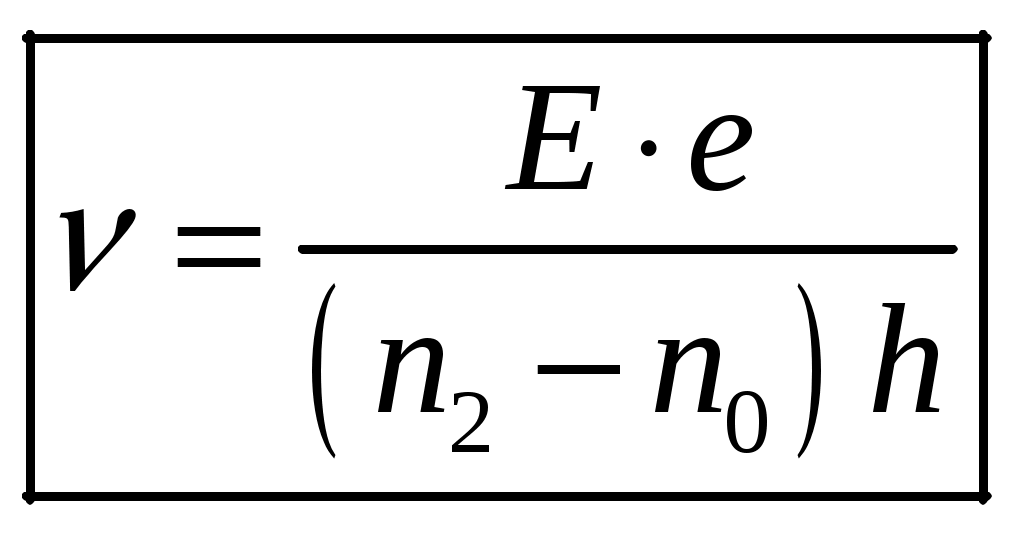

5-1. В некотором водородоподобном атоме электрон может иметь разрешенные значения энергии, определяемые формулой , где . Найти:

A) для серии Лаймана спектра излучения водородоподобного атома ( )

Б) для серии Бальмера спектра излучения водородоподобного атома ( )

B) для серии Пашена спектра излучения водородоподобного атом ( )

а) отношение наибольшей частоты фотона к наименьшей частоте фотона. .

б) отношение наибольшей длины фолны фотона к наименьшей длине вол­ны фотона. .

в) наибольшую частоту фотона. .

г) наименьшую частоту фотона. .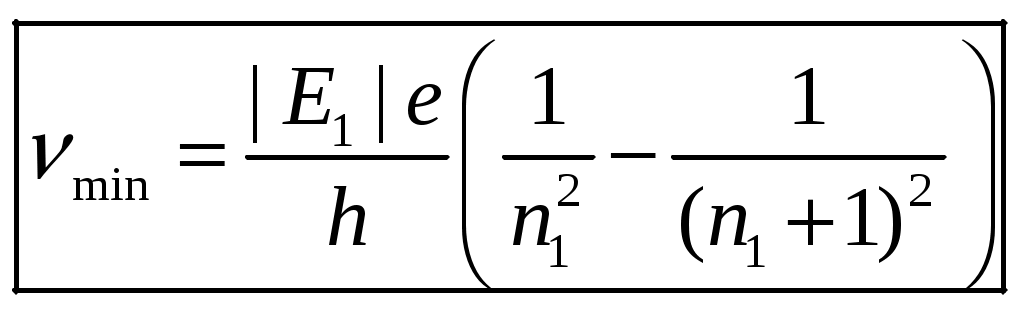

д) наименьшую длину волны фотона (в нм). .

е) наибольшую длину волны фотона (в нм). .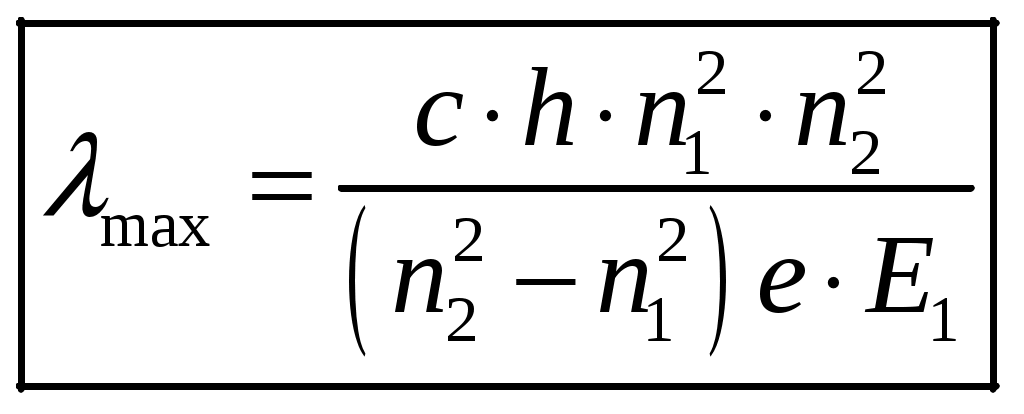

5-2. Во сколько раз минимальная частота фотона из серии Лаймана больше максимальной частоты фотона из серии Бальмера в спектре излучения атома водорода ? . (Ответ: 3)

5-3. Во сколько раз минимальная частота фотона из серии Лаймана больше минимамальной частоты фотона из серии Пашена в спектре излу­чения атома водорода 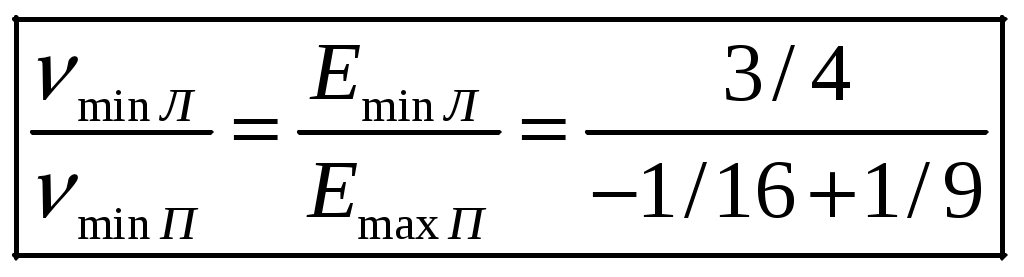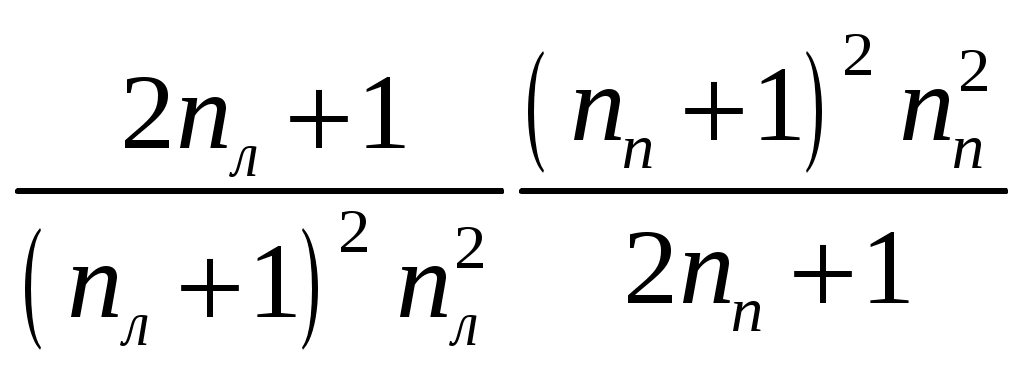? . (Ответ: 15,4)

5-4. Во сколько раз минимальная частота фотона из серии Бальмера больше минимамальной частоты фотона из серии Пашена в спектре излу­чения атома водорода 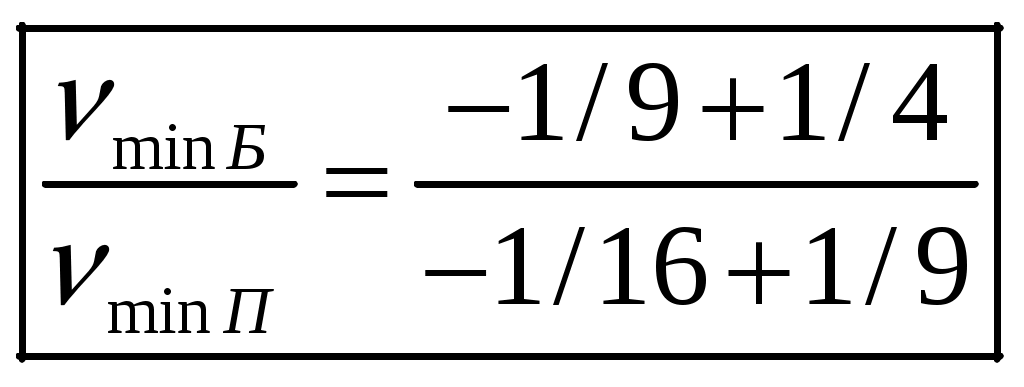? . (Ответ: 2,86)

6-1. В некотором атоме конфигурация электронных оболочек имеет вид: a) ;
б) . Определить максимальную возможную величину суммарной проекции орбитальных моментов импульса всех его электронов на выделенное на­правление.

а) ; б) .

6-2. В некотором атоме конфигурация электронных оболочек имеет вид: . Определить максимальную возможную величину суммарной проекции орбитальных моментов импульса всех его электронов на выделенное направление. .

6-3. Максимальная величина проекции орбитального момента импуль­са некоторого электрона в атоме была равна . Чему равняется:

а) модуль орбитального момента импульса этого электрона. .

б) величина орбитального магнитного момента этого электрона. .

6-4. В некоторой подоболочке (А) некоторой полностью заполненной оболочки атома находится в раз больше электронов, чем в соседней по­доболочке (В) из этой же оболочки. Найти максимальную возможную проекцию орбитального момента импульса электрона

а) из подоболочки А. . б) из подоболочки В .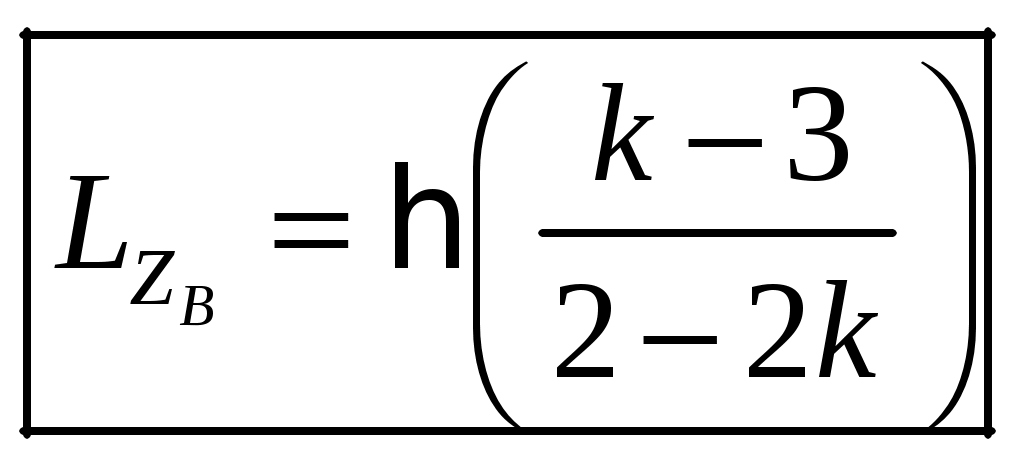

6-5. В некоторой подоболочке (А) некоторой полностью заполненной оболочки атома находится в раз больше электронов, чем в соседней по­доболочке (В) из этой же оболочки. Найти максимальную возможную проекцию орбитального магнитного момента электрона

а) из подоболочки А ; б) из подоболочки В .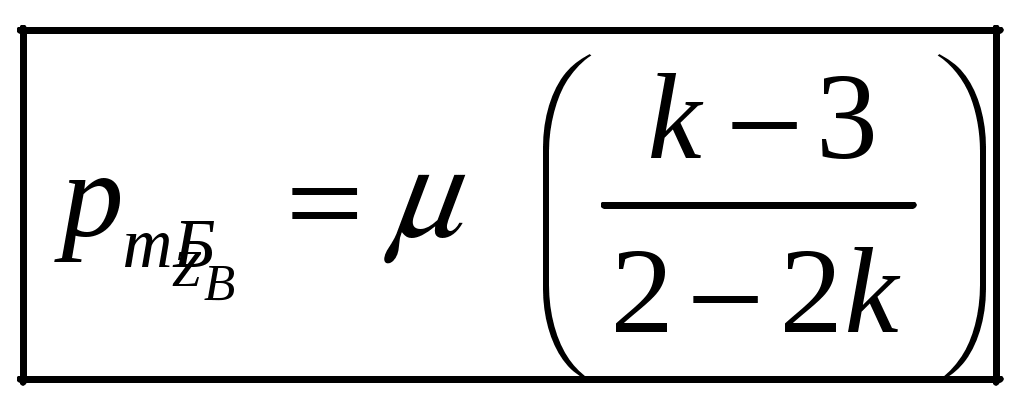

6-6. В некоторой подоболочке ( ) некоторой полностью заполненной оболочки атома находится в раз больше электронов, чем в соседней по­доболочке ( ) из этой же оболочки. Найти минимальное возможное коли­чество электронов во всей оболочке. .

6-7. A)
Б)
B)

а)
б)
в)
г)

6-8. В некоторой подоболочке (А) некоторой полностью заполненной оболочки атома находится в раз больше электронов, чем в сосед­ней подоболочке (В) из этой же оболочки.

а) Во сколько раз больше орбитальный момент импульса электрона из подоболочки А, чем из подоболочки В. .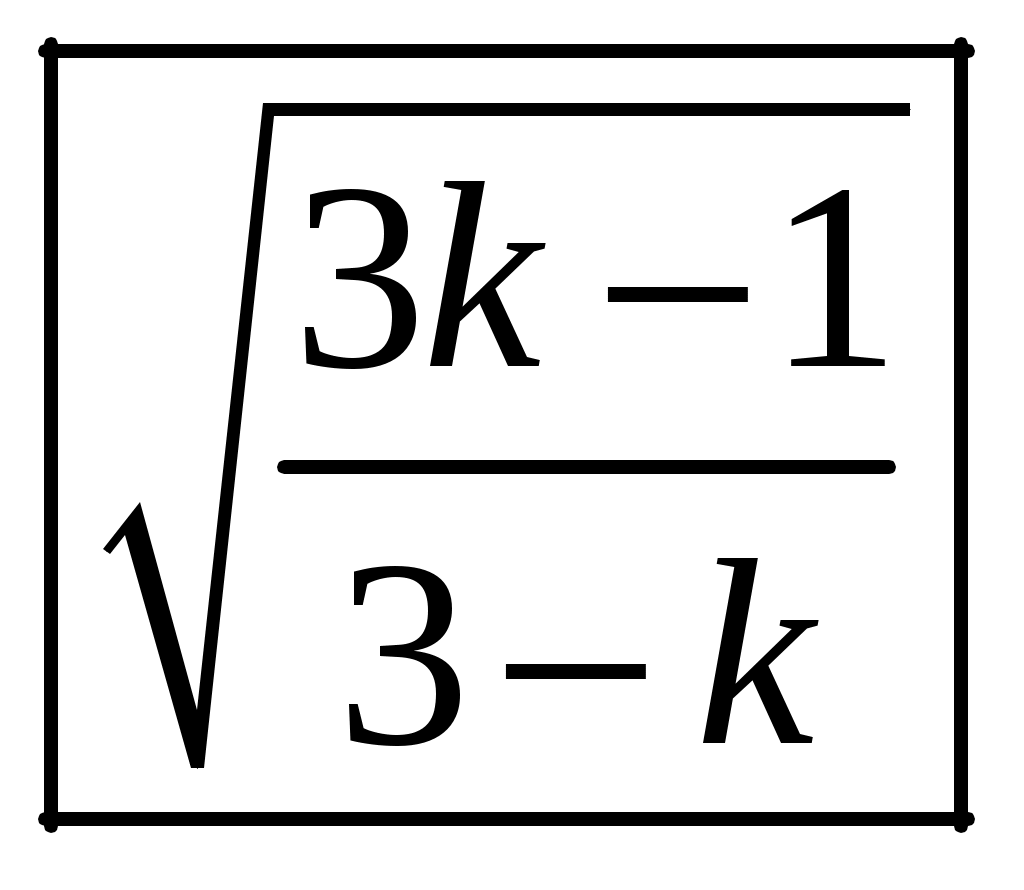

б) Во сколько раз больше орбитальный магнитный момент электрона из подоболочки А, чем из подоболочки В. .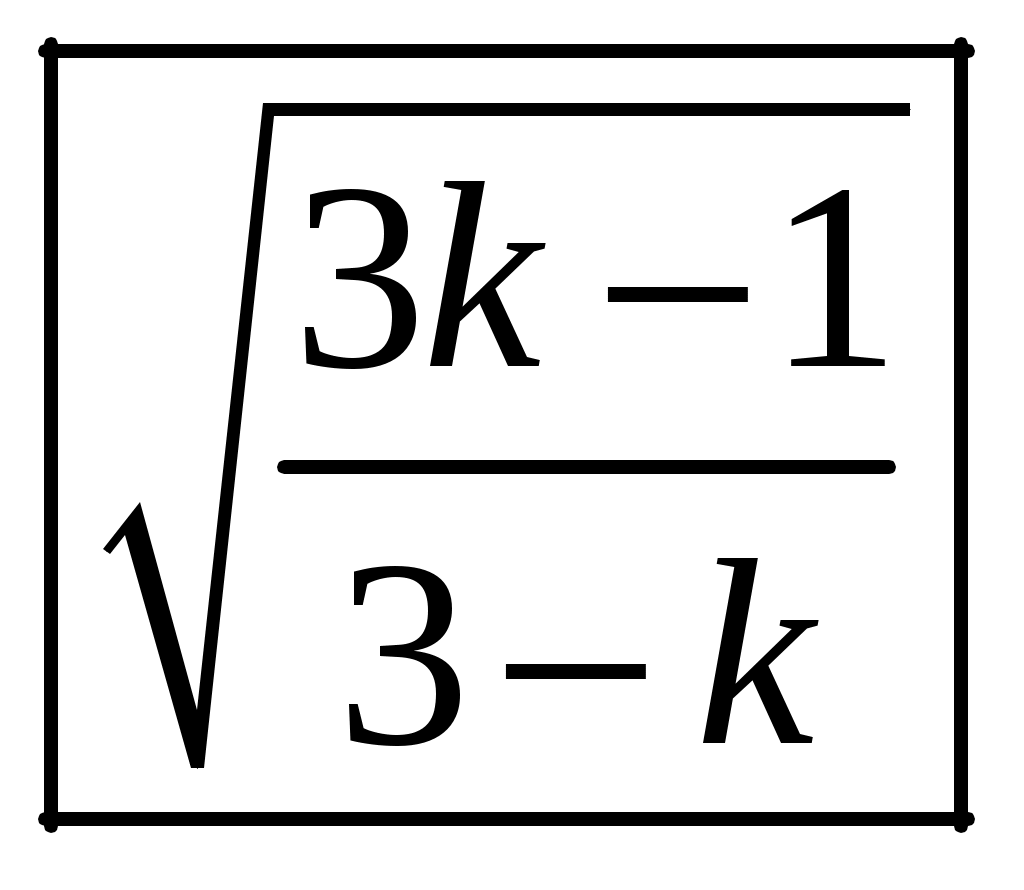

в) Во сколько раз больше орбитальный магнитный момент электрона из подоболочки А, чем его собственный (спиновый) магнитный момент. .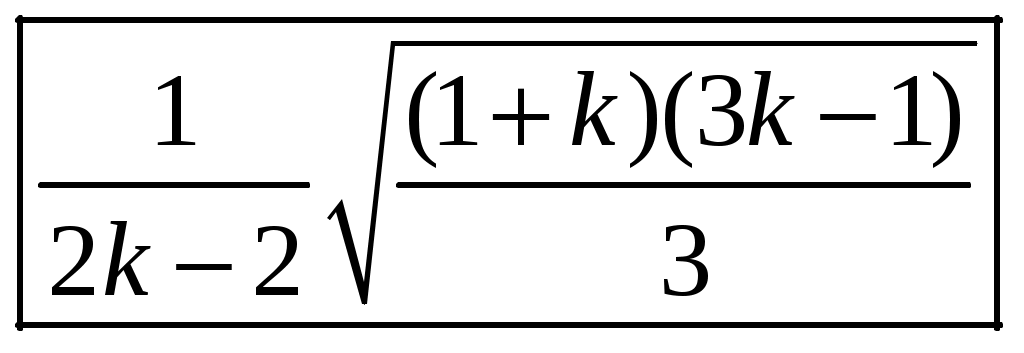

7-1. Ширина запрещенной зоны у кремния (а может быть чего-либо еще) .

а) Во сколько раз возрастет электропроводность кремния (или чего-либо еще) )при нагрева­нии от до ? .

б) На сколько увеличился натуральный логарифм удельной проводи­мости кремния (или чего-либо еще)при нагревании от до ? .

7-2. Найти ширину запрещенной зоны у алмаза (в эВ), если электро­проводность алмаза при нагревании от 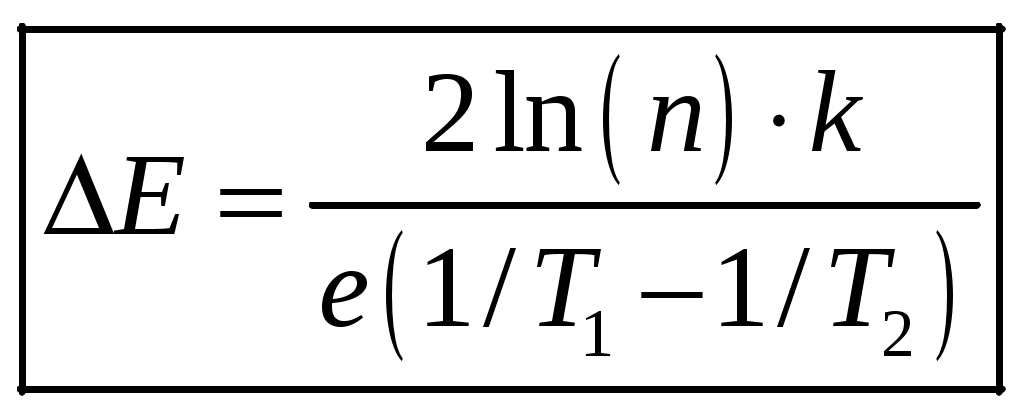до возрастает в п раз. .

7-3. Ширина запрещенной зоны у алмаза . Первоначальная температура алмаза . До какой температуры (в °С) его нагрели, если его электропроводность возросла в раз? .

7-4. Найти ширину запрещенной зоны у собственного полупроводни­ка, если натуральный логарифм его удельной проводимости при нагревании от до увеличился на п? .

7-5. Уровень Ферми в собственном полупроводнике лежит на расстоя­нии выше верхнего уровня валентной зоны. Во сколько раз возрастет электропроводность этого полупроводника при нагревании от до ? .

7-6. На каком расстоянии (в эВ) от нижнего уровня зоны проводимо­сти лежит уровень Ферми в собственном полупроводнике, если электро­проводность этого полупроводника при нагревании от 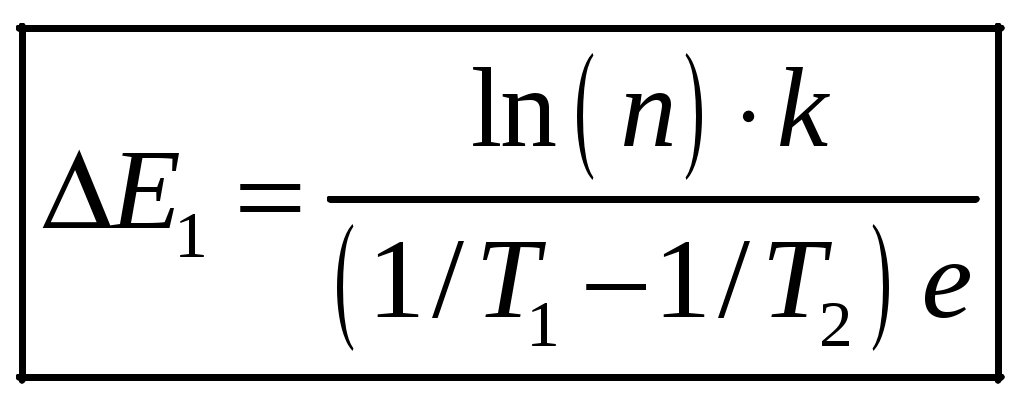до возрастает в п раз? .

7-7. Уровень Ферми в собственном полупроводнике лежит на расстоя­нии 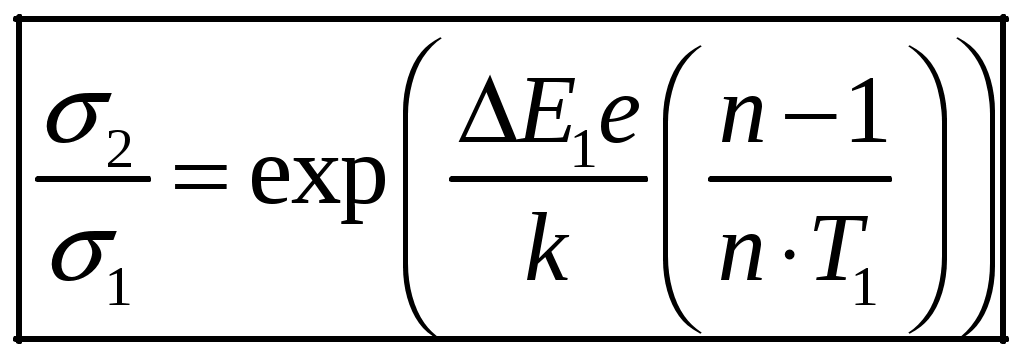выше верхнего уровня валентной зоны. Начальная тем­пература полупроводника . Во сколько раз возрастет электропровод­ность этого полупроводника при увеличении температуры в п раз? .

7-8. Уровень Ферми в собственном полупроводнике лежит на расстоя­нии ниже нижнего уровня зоны проводимости. Натуральный логарифм концентрации свободных носителей заряда в этом полупровод­нике изменился на величину при увеличении температуры в 1,5 раза. Найти начальную температуру полупроводника. .

7-9. Ширина запрещенной зоны полупроводника -типа равна . Акцепторные уровни лежат на расстоянии вы­ше валентной зоны. Концентрация основных носителей заряда в таком полупроводнике при низкой температуре равна . Найти концентра­цию атомов примеси. Считать, что валентность атома примеси на единицу меньше валентности полупроводника. .

7-10. Ширина запрещенной зоны полупроводника -типа равна . Донорные уровни лежат на расстоянии ниже зоны проводимости. Концентрация основных носителей заряда в таком полупроводнике при низкой температуре равна . Найти концентра­цию атомов примеси. Считать, что валентность атома примеси на единицу больше валентности полупроводника. .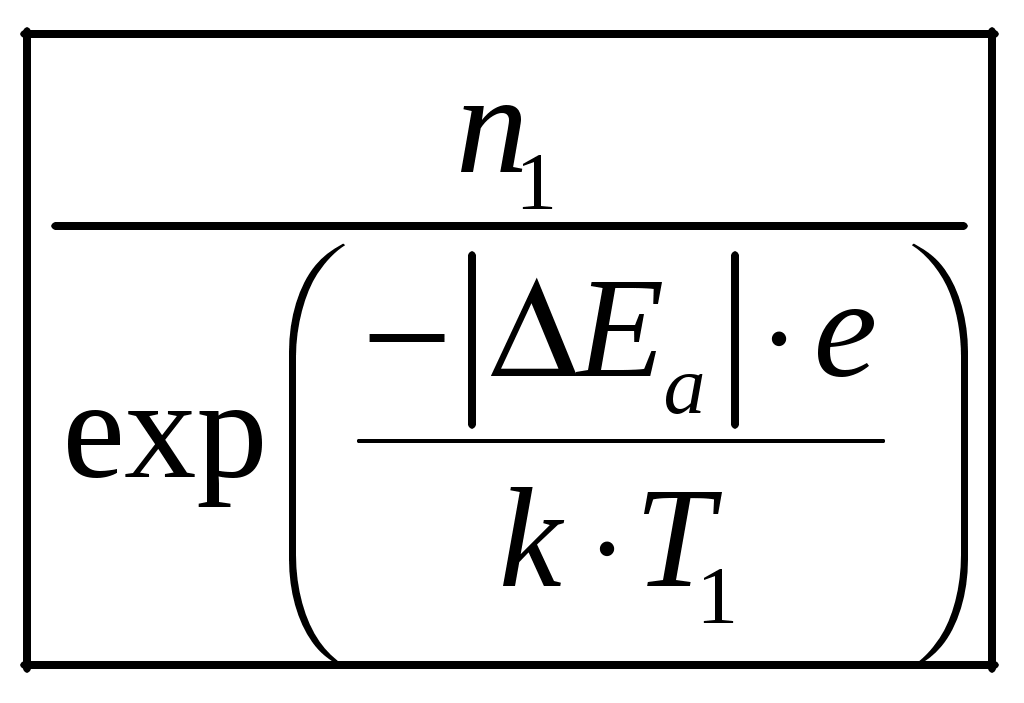

8-1. Распределение Ферми-Дирака для электронного газа в металлах при температуре 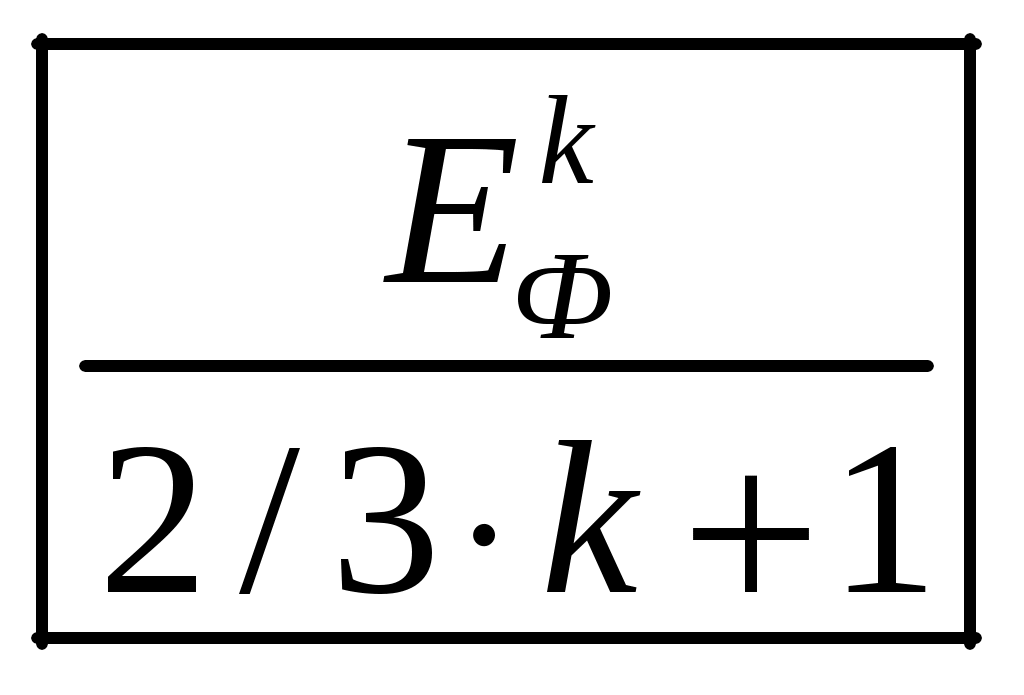задается формулой .Энергия Ферми некоторого металла равна . Для свободных электронов из зоны проводимости проводника при найти:

а) .

б) .

в) .

г) .

8-2. По условию 8-1 найти среднее значение энергии в любой степени.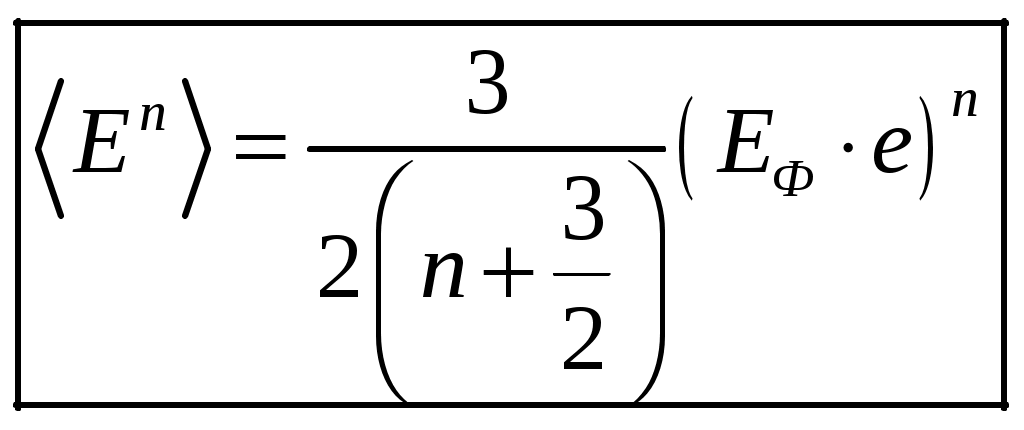

.

8-3. Распределение Ферми-Дирака для электронного газа в металлах при температуре 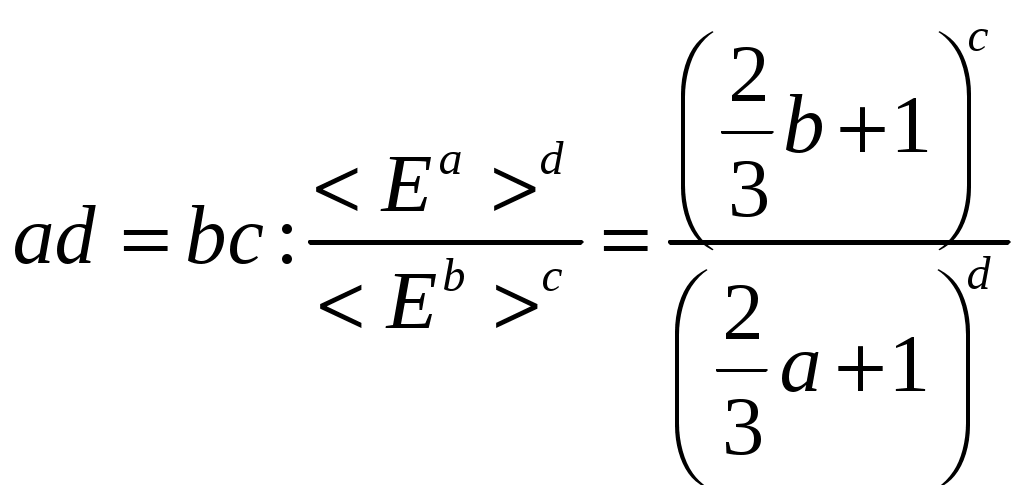задается формулой . Для свобод­ных электронов из зоны проводимости проводника при найти … .
9-1. Радиоактивный образец, содержащий N ядер радиоактивного изо­топа, поместили в герметичный сосуд. Период полураспада этого изотопа равен Т. Сколько ядер образца распадется за промежуток времени от 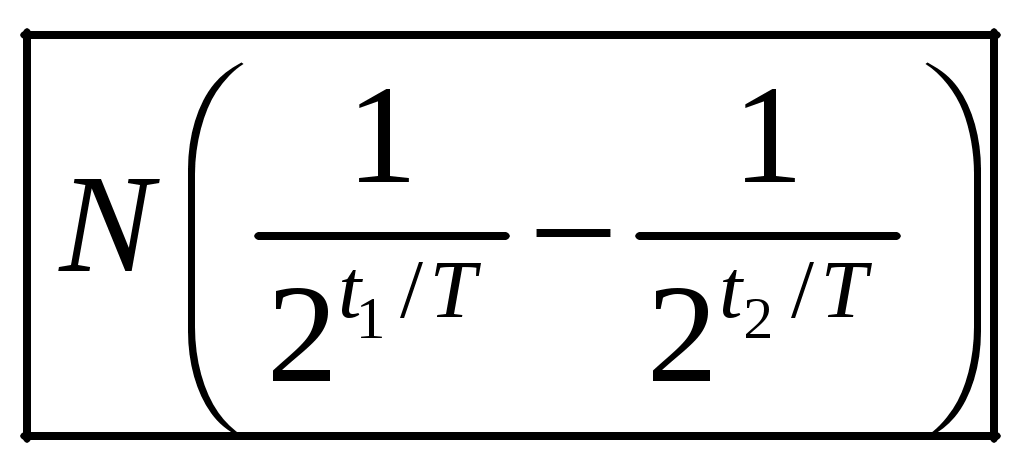до ? .

9-2. Радиоактивный образец, содержащий N ядер радиоактивного изо­топа, поместили в герметичный сосуд. Период полураспада этого изотопа равен T.

а) Сколько ядер образца распадется к моменту времени ? .

б) Сколько ядер образца останется к моменту времени ?

9-3. Радиоактивный образец, содержащий N ядер радиоактивного изо­топа, поместили в герметичный сосуд. Постоянная распада этого изотопа равна .

а) Сколько ядер образца останется к моменту времени ? .

б) Сколько ядер образца распадется к моменту времени ? .

9-4. Радиоактивный образец, содержащий N ядер радиоактивного изо­топа, поместили в герметичный сосуд. Постоянная распада этого изотопа равна . Сколько ядер образца распадется за промежуток времени от

до ? .

9-5. Радиоактивный образец, содержащий N ядер радиоактивного изо­топа, поместили в герметичный сосуд. Среднее время жизни этого изото­па равно . Сколько ядер образца распадется за промежуток времени от

до ? .

9-6. Радиоактивный образец, содержащий ядер радиоактивного изо­топа, поместили в герметичный сосуд. Среднее время жизни этого изото­па равно .

а) Сколько ядер образца распадется к моменту времени ? .

б) Сколько ядер образца останется к моменту времени ? .

9-7. Концентрация ядер одного изотопа с периодом полураспада в раз превышала концентрацию ядер другого изотопа с периодом полурас­пада . Через какой промежуток времени:

а) концентрация ядер этих изотопов станут равными? .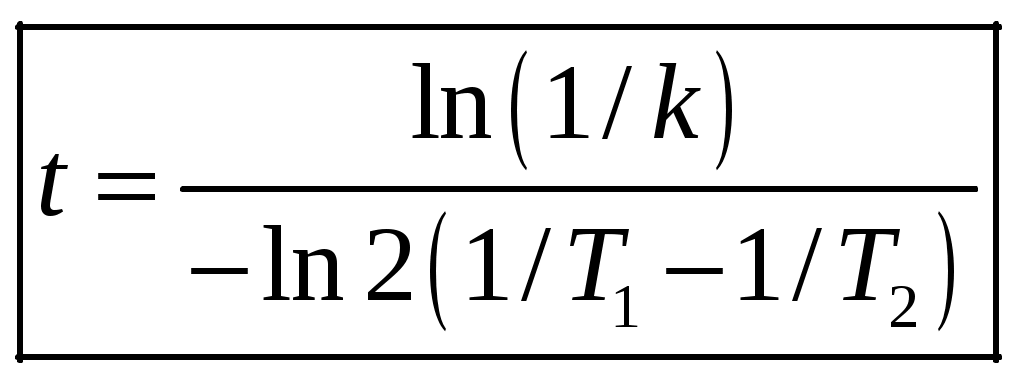

б) концентрация ядер первого изотопа станет в 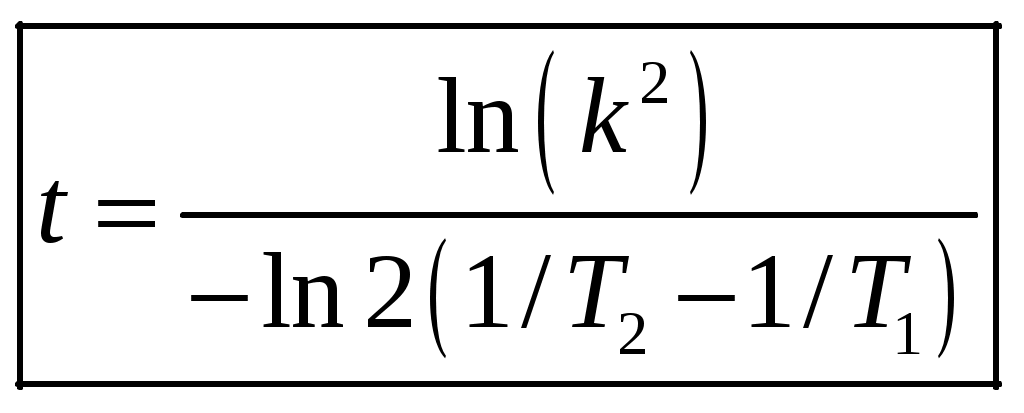раз меньше концен­трации ядер второго изотопа? .

9-8. Концентрация ядер одного изотопа с постоянной распада Х\ в к раз превышала концентрацию ядер другого изотопа с периодом полураспада Т₂. Через какой промежуток времени

а) концентрация ядер этих изотопов станут равными? .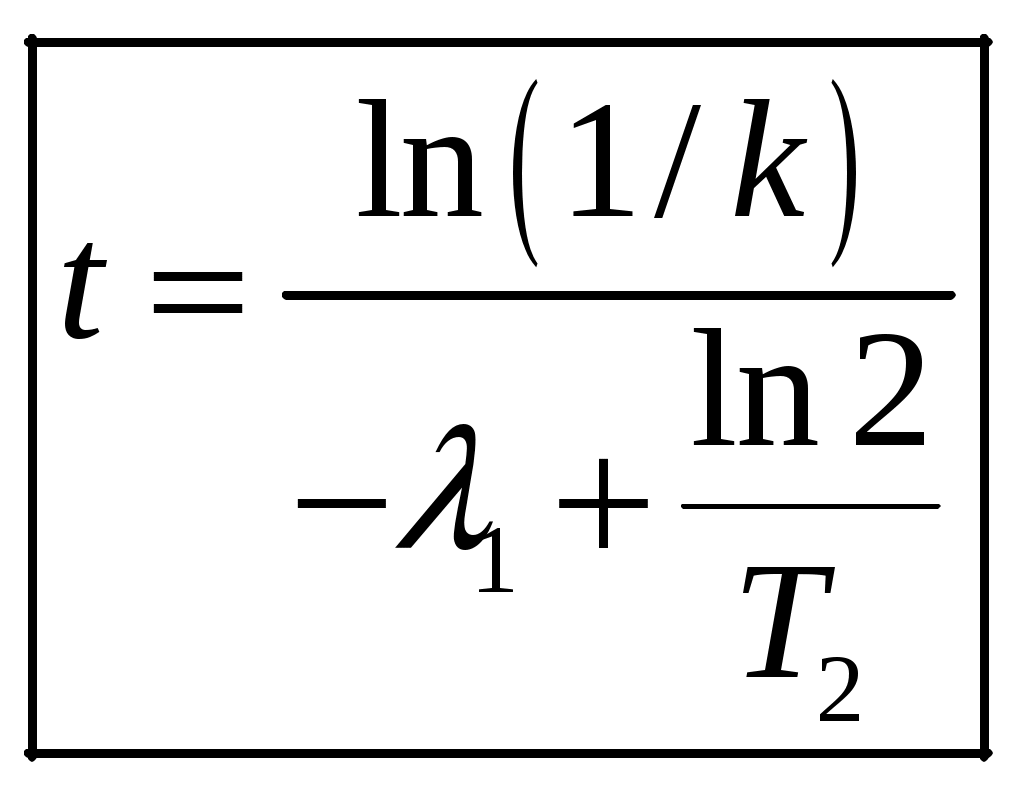

б) концентрация ядер первого изотопа станет в 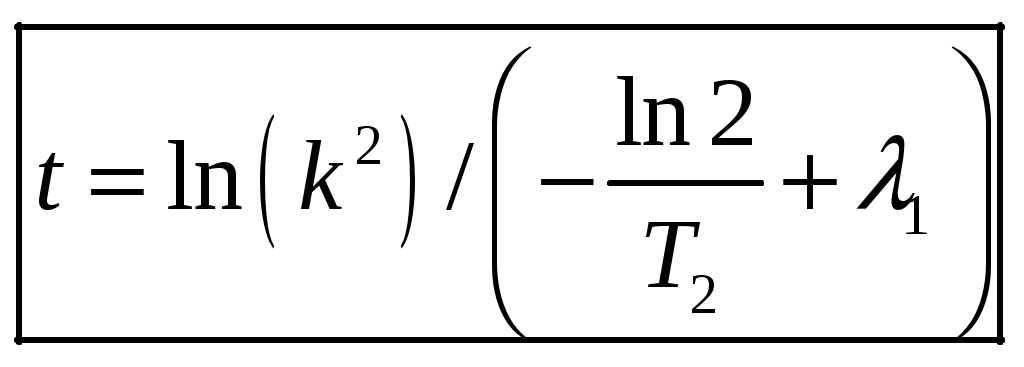раз меньше концен­трации ядер второго изотопа? .

9-9. Энергетический выход реакции деления ядра некоторого неста­бильного изотопа . Сколько тепла (в Дж) выделилось за время t, если первоначальное число ядер этого изотопа , а период полураспада равен Т. .

9-10. Энергетический выход реакции деления ядра некоторого неста­бильного изотопа . Сколько тепла (в Дж) выделилось за время t, если первоначальное число ядер этого изотопа , а постоянная распада равна . .

9-11. Энергетический выход реакции деления ядра некоторого неста­бильного изотопа . Сколько тепла (в Дж) выделилось за время t, если первоначальное число ядер этого изотопа No, а среднее время жизни ядра равно . .

9-12. При распаде ядер радиоактивного изотопа выделилось Qтепла за время t. Первоначальное число ядер этого изотопа 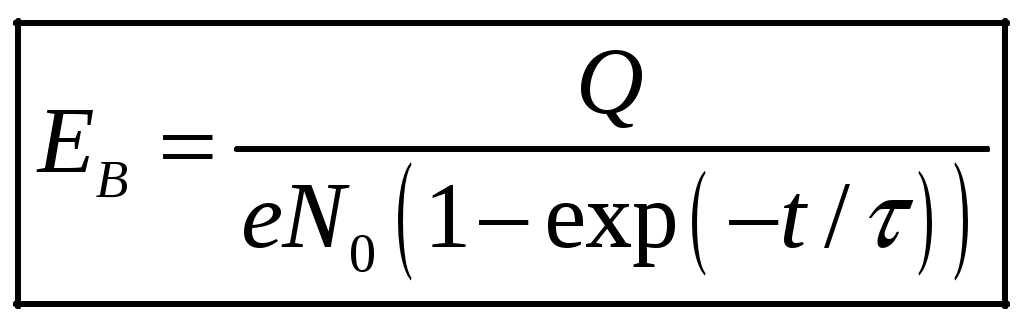, а среднее время жизни ядра равно . Найти энергетический выход (в МэВ) реакции деле­ния одного ядра. .

9-13. При распаде ядер радиоактивного изотопа выделилось Qтепла за время t. Первоначальное число ядер этого изотопа 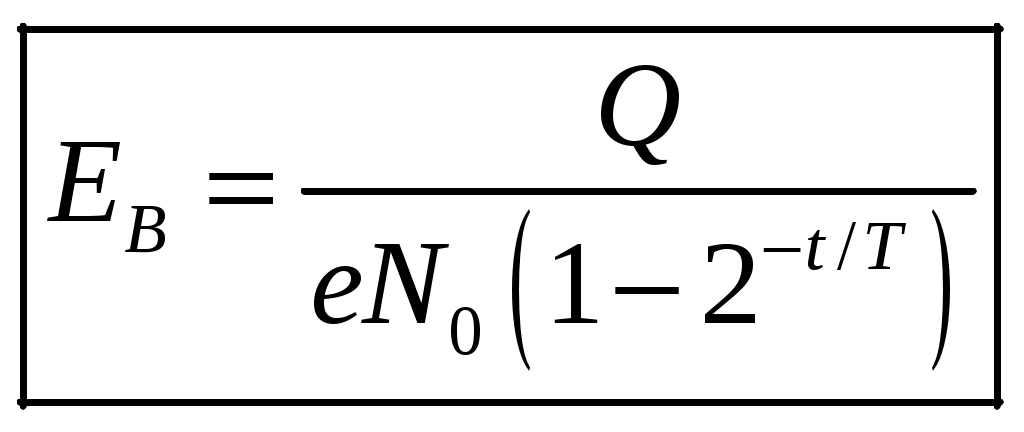, а период полурас­пада равен Т. Найти энергетический выход (в МэВ) реакции деления од­ного ядра. .

9-14. При распаде ядер радиоактивного изотопа выделилось Qтепла за время t. Первоначальное число ядер этого изотопа , а постоянная распа­да равна . Найти энергетический выход (в МэВ) реакции деления одного ядра. .

9-15. При распаде ядер радиоактивного изотопа выделилось Qтепла за время 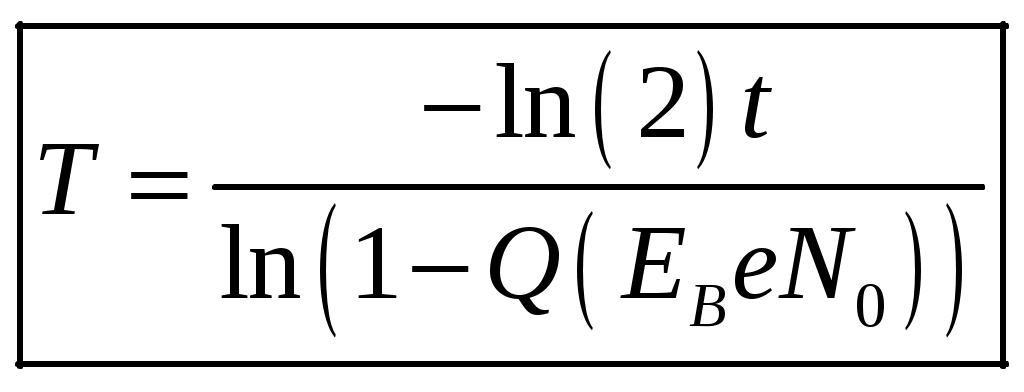. Первоначальное число ядер этого изотопа , энергетический вы­ход реакции деления одного ядра . Найти период полураспада ядер это­го изотопа (в мин). .

9-16. Радиоактивный образец, содержащий изотоп с периодом полу­распада Т, поместили в герметичный сосуд. Сколько процентов ядер об­разца

а) распадется за промежуток времени от до ? .

б) останется через время ? .

9-17. Радиоактивный образец, содержащий изотоп с периодом полу­распада Т, поместили в герметичный сосуд. Через какое время в образ­це останется % радиоактивных ядер этого изотопа? .

9-18. Радиоактивный образец, содержащий изотоп с периодом полу­распада , поместили в герметичный сосуд. Через какое время распа­дется % радиоактивных ядер этого изотопа? .

9-19. Радиоактивный образец поместили в герметичный сосуд. Найти период полураспада ядер этого образца, если через время :

а) распадается 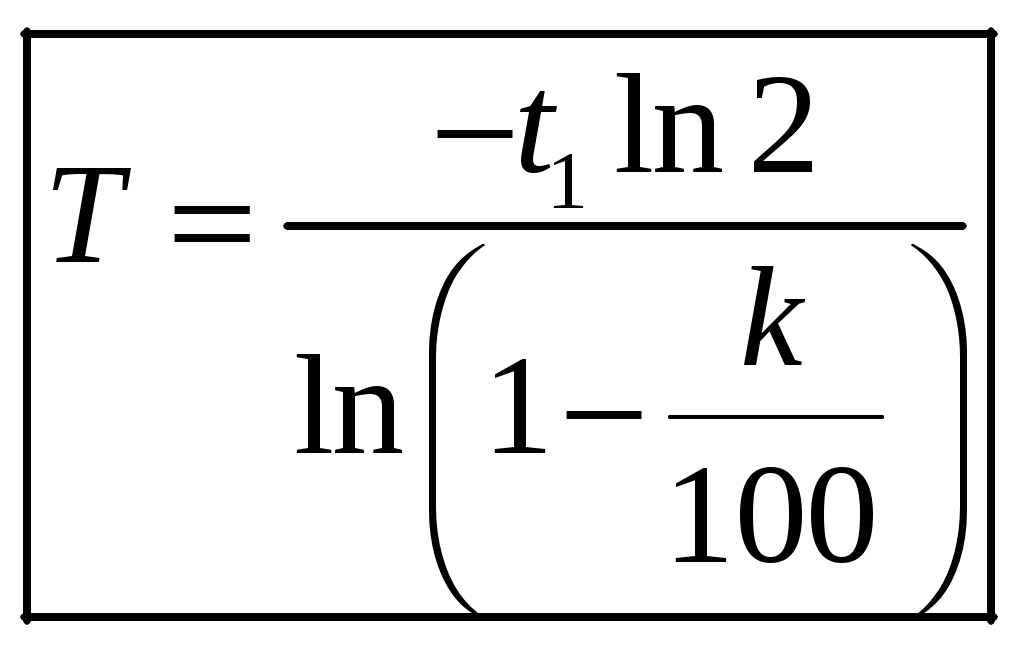% от первоначального количества этих ядер? .

б) останется 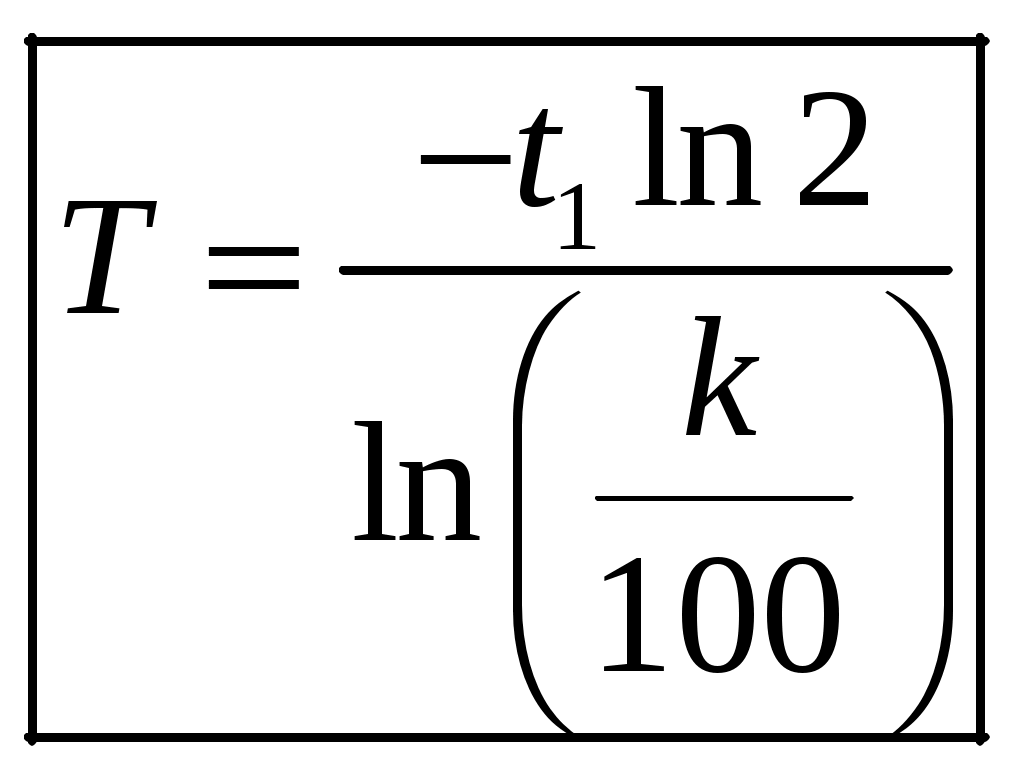% от первоначального количества этих ядер? .

9-20. Радиоактивный образец поместили в герметичный сосуд. Найти постоянную распада ядер этого образца, если через время :

а) распадается % от первоначального количества этих ядер? .

б) останется 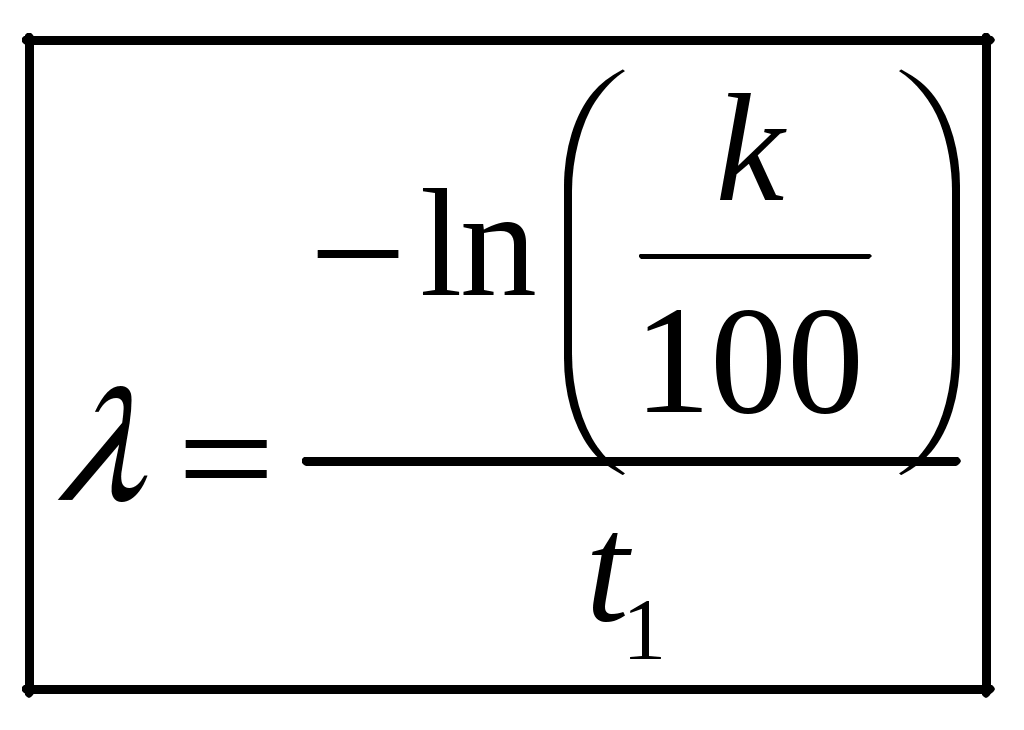% от первоначального количества этих ядер? .

9-21. Радиоактивный образец поместили в герметичный сосуд. Найти среднее время жизни ядер этого образца, если через время 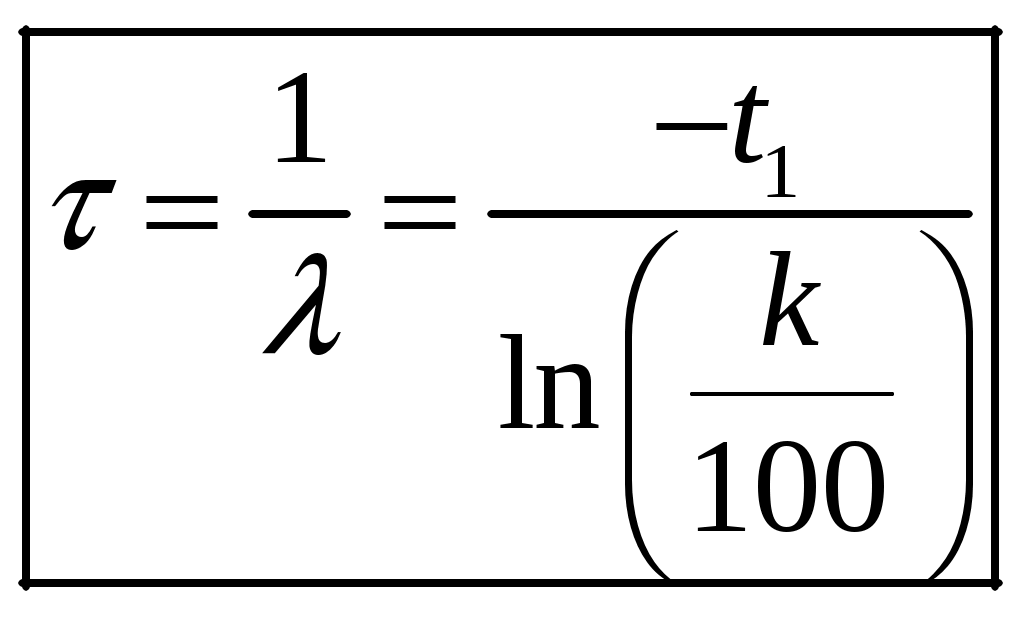ос­танется % от первоначального количества этих ядер? .

10-1. Из эксперимента Резерфода по рассеянию а-частиц на атомах вещества следует, что вся масса атома сосредоточена в очень малой об­ласти пространства, размеры которой не превышают величины м

10-2. Спектры излучения, которые состоят из отдельных узких спек­тральных линий, называются...