|
|
1. Электрмагниттік рекеттесу, оны сипаттамалары. Классикалы электрдинамиканы пні жне дістері, баса физика пндері арасындаы орны
7. Вакуумдағы электрстатикалық өрістің теңдеулері. Электрстатикалық потенциал, оның қасиеттері, нормалау шарты. Нүктелік зарядтың потенциалы.
Вакуумдағы электростатикалық өріс үшін гаусс теоремасы. Электростатикалық өрістердің суперпозициялары принципінің көмегімен электр зарядтары жүйесі өрісінің кернеулігін есептеуді, еркін тұйық бетке толассыз электр өрісінің кернеулік векторының ағынын анықтауға болады. Q нүктелік зарядын қамтитын, r радиусын сфералық бетіне толассыз кернеулік веторының ағыны: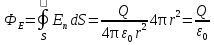
Бұл формула еркін тұйықталған бетке толассыз, вакуумдегі электростатикалық өрістің кернеулік векторының ағыны, 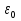 ге бөлінген, зарядтардың осы бетінің ішіндегі алгебралық қосындыға тең ге бөлінген, зарядтардың осы бетінің ішіндегі алгебралық қосындыға тең
8. Пуассон теңдеуі және оның жалпы шешімі
Пуассон теңдеуі
— оператор Лапласа
— вещественная или комплексная функция
Үш еселі декарттық санақ жүйесіндегі теңдеу:
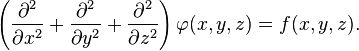
декарттық санақ жүйесінде лаплас операторы түріне озгереді.Яғни,
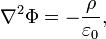 . — электростатический потенциал, —зарядтың көлемдік тығыздығы. . — электростатический потенциал, —зарядтың көлемдік тығыздығы.
9. Электрстатикалық өрістегі өткізгіш. Шекаралық шарттар. Өткізгіш сыйымдылығы. Өткізгіштер жүйесі
Электростатикалық өрістегі өткізгіштер. Өткізгіште заряд тасушылар өте аз күштің әсерінен қозғала алады. Сондықтан өткізгіштегі зарядтардың тепе-теңдігі тек төмендегі шарттар орындалғанда ғана байқалады:
Өткізгіш ішінің барлық жеріндегі өріс кернеулігі нольге тең болуы керек:
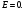
Өткізгіш бетінің әрбір нүктесіндегі өріс кернеулігі бетке нормаль бойымен бағытталған болуы керек:
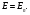
Демек, тепе-теңдік жағдайында өткізгіштің беті эквипотенциалды болады.
Егер өткізетін денеге аздаған q заряд берсек, онда ол тепе-теңдіктің шарттары орындалатындай болып таралады. Дене шегінде толық қамтылған кез келген тұйықталған бетті ойша елестетейік. Зарядтардың тепе-теңдік кезінде өткізгіш ішіндегі кез келген нүктеде өріс болмағандықтан, бет арқылы өтетін электрлік ығысу векторының ағыны нольге тең болады. Гаусс теоремасына сәйкес беттің ішіндегі зарядтардың алгебралық қосындысы да нольге тең болады. Бұл өткізгіштің ішінен қалауымызша жүргізілген кез келген өлшемдегі көлем үшін орынды. Демек, тепе-теңдік кезінде өткізгіштің ішіндегі ешбір жерде артық заряд болуы мүмкін емес, олардың барлығы өткізгіштің бетінде белгілі бір тығыздықпен орналасады.
Өткізгіштің (жеке оқшау өткізгіштің) электрлік сыйымдылығы – өткізгіштен шексіз қашықтықта орналасқан нүктенің электр потенциалы нөлге тең деп қабылданған және басқа барлық өткізгіштер шексіз қашықтықта орналасқан деп ұйғарған жағдайда (жеке оқшау өкізгіш деп аталады) өткізгіш зарядының (Q) оның электр потенциалы (U) қатынасына тең скаляр шама:
С = Q/U.
Жеке оқшау өткізгіш үшін электр сыйымдылық өткізгіштің өлшемдеріне, пішініне, сондай-ақ оқшаулаушы ортаның диэлектрикөтімділігіне (ɛr) тәуелді болады. Екі өткізгіш арасындағы электрлік сыйымдылық (екі өткізгіштің өзара электрлік сыйымдылығы) – өткізгіштер зарядтарының мәндері бірдей, ал таңбалары қарама-қарсы болған жағдайда және басқа барлық өткізгіштер шексіз қашықтықта орналасқан кезде өткізгіштің біріндегі зарядтың абсолюттік мәнінің осы екі өткізгіштің электр потенциалдары айырымыныңқатынасына тең скаляр шама:
С = Q/(ɸ1–ɸ2).
10. Диэлектриктің үйектелуі. Еркін және байланысқан зарядтар. Үйектелу векторы. Сегнетоэлектриктер.
Диэлектриктер - қалыпты жағдайда электр тогын өткізбейтін заттар. Классикалық тұрғыдан қарағанда диэлектриктер өткізгіштерден электр өрісі әсерінен реттелген қозғалыс жасап, электр тогын тудыратын еркін зарядтардың болмауымен ерекшеленеді. Диэлектриктердің атомдарындағы электрондар ядроларымен қатты байланысқан. Бұл байланысты бұзу үшін күшті сыртқы факторлар қажет.
Диэлектриктердің молекулалары электрлі нейтралды, ол қорытқы заряды нөлге тең жүйе сияқты. Осыған қарамастан молекулалардың электрлік қасиеті бар және ол молекулаларды электрлік диполь ретінде қарастыруға болады.
Мұндай дипольдің оң заряды оң зарядтардың «ауырлық центрінде» орналасқан ядроның қорытқы зарядына тең, ал теріс заряды теріс зарядтардың «ауырлық центрінде» орналасқан электрондардың қорытқы зарядына тең. Осындай дипольдің электрлік моменті (– молекуладағы барлық атомдық ядролардағы оң зарядтардың қорытқысы, – электрондардың «ауырлық центрінен» атомдық ядролардағы оң зарядтардың «ауырлық центрін» қосатын вектор).
Диэлектриктерді сыртқы электр өрісіне енгізілгенде сыртқы өріс әсерінен оларда нөлден өзгеше электр моменті пайда болады, яғни диэлектрик үйектелінеді (поляризацияланады).
Сыртқы электр өрісі әсерінен дипольдердің өріс бағытына сәйкес бағдарлану құбылысын диэлектриктердің үйектелуідеп атайды.Нәтижесінде диэлектриктің қандай да бір көлеміндегі электр моменті нолден өзгеше болады.
Диэлектриктер үш топқа бөлінеді: полярлы, полярлы емес және кристалды. Диэлектриктердің бұл үш тобы үйектелудің үш түрімен ерекшеленеді: полярлы емес диэлектриктерде электронды (деформациялы), полярлы диэлектриктерде бағдарланушы (дипольды), ионды кристалдық торлы диэлектриктерде ионды.
Сегнетоэлектриктер — белгілі температуралар аралығында (сегнетоэлектрлік фазаға сәйкес) бағыты сыртқы әсерлер арқылы (электр өрісімен немесе механикалық кернеулермен) өзгертіле алатын спонтанды поляризацияланған кристалл диэлектриктер (соның ішінде сұйық кристаллы).
Ерекшелігі[өңдеу] #
Сегнетоэлектриктерде бір жақты бағытталган спонтанды поляризация аймақтары — сегнетоэлектрлік домендер бар. Сыртқы әсерден Сегнетоэлектриктер көп домендікүйден монодоменді күйге өтуі мүмкін. Сегнетоэлектриктердің осы қасиеті ЕЭМ-ның еске сақтау құрылғыларын жасауда пайдаланылады. Көптеген Сегнетоэлектриктердің диэлектрлік өтімділігі және пьезоэлектрлік константаларының аномальды жоғары мәндері болады және cегнетоэлектриктердің физикалық қасиеттері температураға тәуелді.[1]
11 ,Диэлектриктегі скаляр потенциал. 10да жауабы
12.Электрстатикалық өрістің және зарядтардың өзараәрекеттесу энергиясы
Электромагниттік өріс энергиясының тербеліс жиілігіне тәуелділігі[өңдеу] #
Егер электр заряды 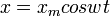 гармоникалық заңдылық бойынша тербелсе, онда оның үдеуі уақыт бойынша гармоникалық заңдылық бойынша тербелсе, онда оның үдеуі уақыт бойынша 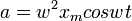 гармоникалық заңдылықпен өзгереді. Электромагнитті толқынды үдемелі қозғалатын зарядталған бөлшек шығарады. Олай болса,толқынның электр өрісінің кернеулігі мен магнит индукциясы үдеуге тура пропорционал. Электр өрісі энергиясының тығыздығы гармоникалық заңдылықпен өзгереді. Электромагнитті толқынды үдемелі қозғалатын зарядталған бөлшек шығарады. Олай болса,толқынның электр өрісінің кернеулігі мен магнит индукциясы үдеуге тура пропорционал. Электр өрісі энергиясының тығыздығы
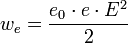
мен магнит өрісінің энергиясының тығыздығы
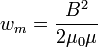
өзара тең. Онда электромагниттік өріс энергиясының тығыздығы 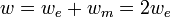 болады. Ендеше, электр өрісінің кернеулігі және магнит өрісінің индукциясы және екенін ескерсек, өрістің энергия тығыздықтары болады. Ендеше, электр өрісінің кернеулігі және магнит өрісінің индукциясы және екенін ескерсек, өрістің энергия тығыздықтары 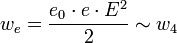 және және 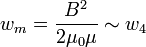 жиіліктің төртінші дәрежесіне пропордионал екені шығады. жиіліктің төртінші дәрежесіне пропордионал екені шығады.
Электромагниттік толкын ағынының тығыздығы немесе толкынның интенсивтілігі жиіліктің төртінші дәрежесіне пропорционал. Электромагниттік өрістің тербеліс жиілігі неғұрлым жоғары болса, толқынның интенсивтілігі, яғни бірлік ауданға келетін қуат соғұрлым артады.
13. Сыртқы өрістергі дипольдің энергиясы.
Қозғалмайтын зарядтардың электр өрiсiн электростатикалық деп атайды. Ол тек электр зарядтарынан пайда болады және уақыт бойынша өзгермейдi. Электр өрiсi осы зарядтармен қоршаған кеңiстiкте бар болады және онымен үздiксiз байланыста болады. Электр диполiнiң негiзгi сипаттамасы диполь (электр) моментi деп аталатын векторлық физикалық шама болып табылады. Бұл моменттiң модулi заряд q модулiнiң арақашықтыққа L көбейтiндiсiне тең: . Сыртқы электростатикалық өріске орналасқан электрлік дипольдің энергиясын қарастырсақ. Алдымен сырты электростатикалық өрісте орналасқан екі дипольді аламыз. Олардың кернеулігі E1 және E2 тең. Ал потенциалы φ1 және φ2 тең деп аламыз. Сыртқы электростатикалық өріске орналасқан электрлік дипольдің энергиясы мынаған тең болады: U= -eφ1+eφ2=e{φ2- φ1}=e.δφ /δl.l=Pgradlφ, E=-gradφ, -gradlφ=El, U=pEl, U= -pEl=-(pE), p↑↑E.
14. Электрстатикалық өрістегі механикалық күштер.
Электрстатикалық өрісте сыншы Q0 зарядты шексіз аз орын ауысты-руда кулондық күштердің атқаратын элементар жұмысы:
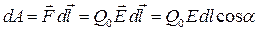 . (104) . (104)
Нүктелік Qзарядтың электрстатикалық өрісінде Q0 зарядтың шексіз аз орын ауыстыруында атқарылатын элементар жұмыс:
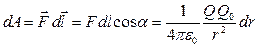 , ,
ал 1 нүктеден 2 нүктеге орын ауыстыруда атқарылатын жұмыс:
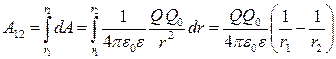 . .
Кез келген L тұйық контур бойында Qзаряд айнала қозғалғанда:
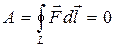 . (105) . (105)
векторының циркуляциясы туралы теорема: Электрстатикалық өріс кернеулігі векторының кез келген тұйық контур бойымен циркуляциясы нөлге тең болады:
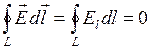 . (106) . (106)
Электрстатикалық өрісқұйынсыз болғандықтан, Стокс теоремасына сәйкес, кернеулігі мына шартты қанағаттандырады: . Бұл вакуумде және затта тек электрстатикалық өріс үшін ғана орындалады.
Сыншы нүктелік Q0 зарядтың нүктелік Q1, Q2, Q3, ..., QN зарядтар жүйесінің өрісіндегі потенциалдық энергиясыжеке зарядтарға қатысты потенциалдық энергиялардың қосындысына тең:
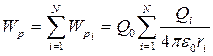 . (107) . (107)
Электрстатикалық өрістің потенциалы–сан жағынанөрістің нақты нүктесінде орналасқан бірлік зарядтың потенциалдық энергиясына тең:
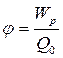 . (108) . (108)
Электрстатикалық өріс күштерінің сыншы Q0 зарядты өрістің бір нүктесінен екінші нүктесіне орын ауыстыруда атқаратын жұмысыбастапқы және соңғы нүктелердің потенциалдар айырымын сыншы заряд шамасына көбейткенге тең:
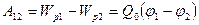 (109) (109)
15. Заттағы Максвелл теңдеулерінің формальді жүйесі, шекаралық шарттар.
Максвелл теңдеуі- классикалық электродинамиканың негізгі теңдеулері; кез келген ортадағы жэне вакуумдағы барлық электромагнит/электромагниттік кұбылыстарды толығымен сипаттайды, өріс көздерінің, электр зарядының жэнетоктардың орналасуы мен козғалысы аркылы электромагниттік өрісті сипатгайтын шамалар өзгерісін байланы- стыратын төрт тендеулер жүйесінен тұрады.Электромагниттік өріс теориясының негізін Максвелл теңдеулері деп аталатын теңдеулер жүйесі құрайды. Бұл теорияныңматематикалық аппараты күрделіболғандықтан, олтеңдеулердіқарастырмаймыз.
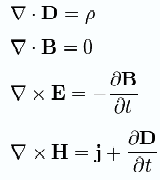
Изоторпты және дисперция жоқ ортадағы Максвелл теңдеулері:
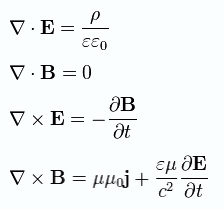
16.Вакуумдағы магнитстатиканың теңдеулері, олардың түсіндірмесі. Векторлық потенциал.
Уақыттан тәуелсіз магнит өрісі магнитстатикалық өріс д.а. Бұл жағдайда магнит өрісін электр өрісінен бөліп қарауға болады. Магнитстатикалық өріс үшін, Максвелл теңдеулерін келтірейік
rotH=j (1.1)
divB=0 (1.2)
B=µaH (1.3)
Bn2-Bn1=0 (1.4)
Hr2-Hr1= iбет (1.5)
1.1-теңдеуі магнитстатикалық өрістің потенциалдық емес құйынды өріс екендігін білдіреді.
1.2-теңдеуі магнит индукция сызықтарының тұйық екендігін білдіреді.
1.3-өрнегі магнит өрісі кернеулігін магнит индукциясымен байланысты.
1.4 және 1.5 екі екі ортаның шекаралық шарттарын өрнектейді.
1.4-өрнегі екі орта шекарасында магнит индукциясының нормаль құраушысының үзіліссіздігін білдіреді.
1.5- екі орта шекарасында магнит өрісі кернеулігі немесе жанама құраушысының мәндерінің үзілетіндігін көрсетеді.
Векторлық потенциал-құйынды векторлық өрісті сипаттауға арналып қолданылатын векторлық функция. Потенциал-физикалық күш өрістерінің кең көлемді тобын (электрлік, гравитатциялық, т.б.) және физикалық шамалардың векторымен көрсетілген өрістерін(сұйықтық жылдамдығының өрісі, т.б.) сипаттайтын ұғым. Әрбір векторлық шама а өзінің потенциалының градиентіне тең а=gradj. Мұндай жағдайда векторлық өрісті потенциялдық деп атайды. Векторлық өріс кестесінің әрбір нүктесінде вектор болатын функциямен сипаттайтын физикалық өріс.
17.Векторлық потенциалға арналған Пуассон теңдеуі, оның толық шешімі.
1.1 Магнит өрісінің векторлық потенциалы үшін Пуассон теңдеуі.
▼2А=-µaj (1.1)
1.1-Теңдеудің жалпы шешімін мына түрде жазуға болады.

▼2φ= -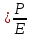 (1.2) (1.2)
1.2-дегі Пуассон теңдеуін Оpтада электр заряды жоқ болған жағдайда қолданамыз.
18.Станционарлық магнит өрісінің магниттік дипольді жуықтаумен қарастырылуы.Магниттік момент.
Магниттік диполь электрлік диполь – шамалары тең, l ара қашықтығы өрісанықталатын нүктеге дейінгі қашықтықпен салыстырғанда едәуір аз. дипольдің электрлік моменті (дипольдік момент)–дипольдің иінімен бағыттас, заряд модулі мен иіннің көбейтіндісіне тең шама. Таралуы тұйық контурмен ағатын электр тогы жасаған магнит өрісінің таралуымен сәйкес келетін өрісті жасайтын, өлшемі өзінен өрістің қарастырылатын нүктесіне дейінгі қашықтықпен салыстырғанда өте кіші болатын магнит өрісінің кезі.
Магниттік момент — заттың магниттік қасиеттерін сипаттайтын негізгі шама. Электр-магниттік құбылыстардың классикалық теориясына сәйкес магнетизмнің (Магниттік моменттің) көзі электр макротоктар және микротоктар (атомдық) болып табылады. Магнетизмнің қарапайым көзі ретінде тұйық ток алынады. Электр-магнит өрістің классикалық теориясы және тәжірибелік деректер бойынша тұйық токтың (тогы бар контурдың) магнит әсері ток күші (і) мен контур ауданының () көбейтіндісі (М) белгілі болғанда ғана анықталады:М=і/с (бірліктердің СГС жүйесінде).Анықтама бойынша М векторы Магниттік момент болып табылады. Оны электрлік диполь моментіне ұқсастырып, М=ml, түрінде жазуға болады: мұндағы m — контурдың эквиваленттік магнит заряды, l — қарама-қарсы таңбалы “магниттік зарядтардың” ара қашықтығы.
19) Магнетиктер. Магниттелу векторы. Магнетиктегі магнит өрісінің векторлық потенциалы.
Магниттік өріске орналасқан бүкіл заттар магниттеледі. Кез келген дене магнетик болып саналады, яғни ол магниттік өріс әсерімен магниттелуге қабілетті. Осы құбылыстың механизмін түсіну үшін мына суретті қарастырайық:

Атомдағы электрон дөңгелек орбита бойынша қозғалады деп аламыз. Электрон орбитасы В векторға қатысты альфа бұрыш жасап қозғалса, онда ол В шеңберінде осындай қозғалыс жасайды деп дәлелдеуге б-ды.Осылайша атомның электрондық орбиталары сыртқы магниттік өріс әсерімен, дөңгелек токқа эквивалентті прецессиялық қозғалыс жасайды. Ленц ережесіне сәйкес, атомда сыртқы өріске қарама-қарсы бағытталған құраушы магниттік өріс пайда б-ды. Заттар магнетиктер, диамагнетиктер ж/е ферромагнетиктер деп бөлінеді.
Диэлектриктердің үйектелуін сандық сипаттауға ұқсас, магниттердің магниттелуін сипаттайтын векторлық шама-магниттелушілік (магниттелу) енгізілді:
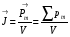
Pm-магнетиктің магниттік мезеті. V-магниттелу көлемі.
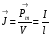
Магниттелу біртекті өріс жағдайында :
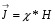
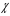 - магниттік қабылдағыштық. - магниттік қабылдағыштық.
|
|
|
 Скачать 0.89 Mb.
Скачать 0.89 Mb.