1. Электрмагниттік рекеттесу, оны сипаттамалары. Классикалы электрдинамиканы пні жне дістері, баса физика пндері арасындаы орны
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
Магниттік өрістің векторлық потенциалы: Векторлық потенциал - құйынды векторлық өрісті сипаттауға арналып қолданылатын векторлық функция. 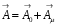 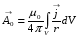 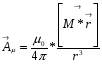 20) Магнит өрісінің энергиясы. Магнитстатикалық өрістің энергиясын токтар шамасы, өздік және өзара индукция коэффициенттері арқылы өрнектеу Соленоидқа Е батареяны тұйықтасақ, ол арқылы ток жүреді, онда i тогы тұрақтанады да, соленоидтың орамдарында магнит өрісі туындайды. Батареяны R кедергімен алмастырсақ, ток кеми бастайды. Осы токпен істелетін жұмыс: 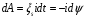 , егер L=const болса, dA=-Ldi. , егер L=const болса, dA=-Ldi. Осыдан: 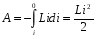 Сөйтіп I тогы ағатын өткізгіш 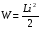 энергияға ие б-ды. энергияға ие б-ды.Магнитстатикалық өріс. Токтар шамасы арқылы: 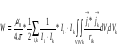 Өзара, өздік индукция коэф. арқылы: 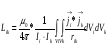 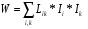 21) Магнитстатикалық өрістегі күштер. Шекаралық шарттар Магнитстатика-тұрақты токтардың өзара әсерлесуін магнит өрісі арқылы зерттейтін (есептейтін) классикалық физиканың бөлімі. Уақыттан тәуелсіз магнит өрісі магнитстатикалық өріс деп аталады. Бұл жағдайда магнит өрісін электр өрісінен бөліп қарауға болады. Магнитстатикалық өріс потенциалдық емес, ол-құйынды өріс. Магнитстатикада Био-Савар-Лаплас заңы, магнит өрісі циркуляциясы туралы теорема, Лоренц, Ампер күштері формула-ы қолданылады. Бөгде күштер әсер ететін жағдайдағы Ом заңы: 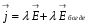 Джоуль-Ленц: 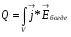 Био-Савар-Л.: 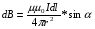 Екі токтың өзара әсері: 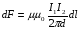 Ампер: 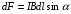 22. Электрмагниттік өріске арналған Максвелл теңдеулері жүйесінің интегралдық және дифференциалдық түрлері. Максвелл теңдеулерінің физикалық мағынасы. Максвелл теңдеулері жүйесі қасиеттері. Максвелл теңдеулерінің интегралдық түрі Максвелл теңдеулері интегралдардың көмегңмен де жазылуы мүмкін: 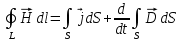 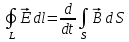 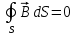 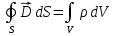 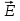 және және  векторлары өрістер айнымалы болса ғана байланыста болатындығын ерекше атап өткен жөн. Егер стационарлық өрістермен шектелсек, яғни векторлар уақытқа тәуелсіз болса векторлары өрістер айнымалы болса ғана байланыста болатындығын ерекше атап өткен жөн. Егер стационарлық өрістермен шектелсек, яғни векторлар уақытқа тәуелсіз болса 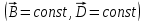 , онда өрістер теңдеуінен , онда өрістер теңдеуінен 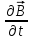 және және 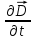 алынып тасталады. Сондықтан өрістің дифференциалдық теңдеулер жүйесі екі тәуелсіз жүйелерге ыдырайды. алынып тасталады. Сондықтан өрістің дифференциалдық теңдеулер жүйесі екі тәуелсіз жүйелерге ыдырайды.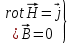 стационарлы магнит өрісінің теңдеулерінің жүйесі стационарлы магнит өрісінің теңдеулерінің жүйесі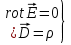 электростатикалық өріс теңдеулерінің жүйесі. электростатикалық өріс теңдеулерінің жүйесі.Осы екі теңдеулер жүйесінің бір-біріне тәуелсіздігі электростатикалық және стационарлық магнит өрістерін жеке-жеке зерттеуге мүмкіндік береді. 3 Максвелл теңдеулерінің дифференциалдық түрі Максвелл теңдеулері сызықты дифференциалдық теңдеулер болғандықтан, оның дербес шешімдерінің қосындысы да сол теңдеулердің шешімі болады. Мұны векторлық өрістер үшін суперпозиция принципі деп атайды және есеп шығарған кезде жиі қолданылады. Теңдеулердің дифференциалдық түрін жазайық. Максвелдің бірінші теңдеуі: 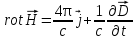 Максвелдің екінші теңдеуі: 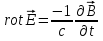 Индукция векторының дивергенциясы үшін теңдеу төмендегідей болады: 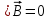 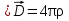 Үзіліссіз теңдеу 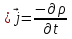 Материалдық теңдеу 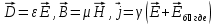 4 Максвелл теңдеулерінің физикалық мағынасы Максвелл теңдеулерінің физикалық мағынасына тоқталу үшін оларды екі жұпқа топтастырайық: Дифференциалды түрі 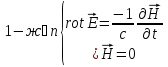 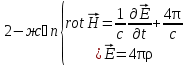 Интегралдық түрі 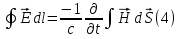 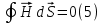 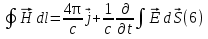 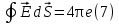 Токтар мен зарядтардың үлестірулерін белгілі деп алып, Максвелл теңдеулерінің көмегімен 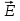 және және  векторларының тәуелсіз алты құраушысын табуға болады. Максвелдің сегіз скалярлық дифференциалдық теңдеулер жүйесінде алты тәуелсіз теңдеулер бар. (4) теңдеуі Фарадейдің индукция заңының жалпылама түрін беріп, уақыт бойынша магнит өрісінің өзгерісі құйынды электр өрісіні туғызатындығын көрсетеді. (5) теңдеуі магнит өрісінің мінездемесі соленойдалы және оның сызықтары тұйық немесе шексіздікке кететіндігін дәлелдейді. (6) теңдеуінен құйынды магнит өрісі зарядтардың қозғалысынан және уақыт бойынша электр өрісінің өзгерісінен туындайтындығын көреміз. (7) теңдеуі электр өрісінің көзі электр зарядтары болып табылатындығын көрсетеді. векторларының тәуелсіз алты құраушысын табуға болады. Максвелдің сегіз скалярлық дифференциалдық теңдеулер жүйесінде алты тәуелсіз теңдеулер бар. (4) теңдеуі Фарадейдің индукция заңының жалпылама түрін беріп, уақыт бойынша магнит өрісінің өзгерісі құйынды электр өрісіні туғызатындығын көрсетеді. (5) теңдеуі магнит өрісінің мінездемесі соленойдалы және оның сызықтары тұйық немесе шексіздікке кететіндігін дәлелдейді. (6) теңдеуінен құйынды магнит өрісі зарядтардың қозғалысынан және уақыт бойынша электр өрісінің өзгерісінен туындайтындығын көреміз. (7) теңдеуі электр өрісінің көзі электр зарядтары болып табылатындығын көрсетеді.Қасиеті;Максвелл теңдеулері – кез келген ортадағы электромагниттік құбылысты сипаттайтын классикалық макроэлектродинамиканың діңгекті теңдеулері. Максвелл теңдеулері электр зарядтары мен токтардан, электр және магнит индукцияларынан туындаған электромагниттік өрістердің өзара байланыстарын сипаттайды. 23. Электрмагниттік өрістің потенциалдары Сан мәні зарядты өpicтiң берілген нүктесінен шексіздікке дейін қозғаған кезде істелетін жұмыстың осы зарядтың шамасына катынасына тең болатын энергетикалық сипаттаманы электростатикалық өрістің потенңиалы деп атайды; 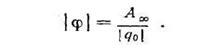 Бұл анықтама теория жүзіндегі анықтама болып табылады. Зарядты жер бетінен өpicтiң берілген нүктесіне дейін қозғаған кезде істелетін жұмыстың осы зарядтың шамасы на катынасынэлектростатикалық өрістің потенңиалы деп атайды. Зарядты өpicтiң потенңиалы 1 болатын нүктесіен потенңиа лы 2 болатын нүктесіне дейін қозғаған кезде істелетін жұмыс тың осы заряд шамасына қатынасын потенңиалдар айырымы (ф1 —ф2) деп атайды: 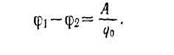 24) Лоренц шарттары. Потенциалдарға арналған теңдеулер Қозғалыстағы зарядталған бөлшектерге магнит өрісі тарапынан әсер ететін күш Лоренц күші деп аталады. FЛ = qυB sin α. 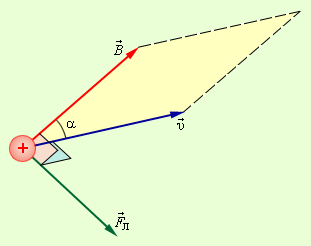 Мұндағы - В және векторлары арасындағы бұрыш. Ампер күшінің бағыты секілді, Лоренц күшінің бағыты сол қол ережесімен анықталады. Біртекті магнит өрісінде оның индукциясына перпендикуляр жылдамдықпен қозғалған зарядты бөлшекке модулі жағынан тұрақты, жылдамдыққа перпендикуляр бағытталған Лоренц күші әсер етеді. Лоренц күшінің әсерімен бөлшек центрге тартқыш үдеу алады және шеңбер бойымен қозғалады, мұнда Лоренң күші жұмыс істемейді. Шеңбердің радиусы: 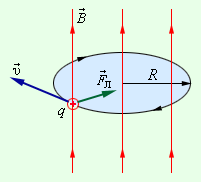 Электр тогы-зарядалған бөлшектердің реттелген бағытталған қозғалысы.Токтың бағытына оң зарядталған бөлшектердің қозғалыс бағыты алынады.Токтың әсері: 1)боймен ток жүрген өткізгіш қызады.2)химиялық әсері байқалады.3)Магниттік әсері байқалады.Электр тогы болу үшін мына шарттар орындалу қажет:1)Зарядталған бөлшектер q.2)Өріс тарапынан әсер ететін күш болу керек(F=qE).3)Электр өрісі Е.4)Потенциял айырмасы U болу керек.
Сыртқы магнит өрісі -де орналасқан ток элементі Idl -ді қарастырайық.Бұл векторлардың арасындағы бұрышыт болсын.Ампер күшіне сәйкес Idl элементіне мынадай күш әсер етеді dF=BIdl мұндағы ток күші I= Осы бірінші өрнекті екіншісіне қою нәтижесінде мынаны шығарып аламыз:dF=BdlN Fn= Векторлық формада өрнегі былайша жазылады,яғни Магнит өрісінде қозғалатын зарядқа әсер ететін күш =const және qB= Өрнекөрісіндегі зарядтың қозғалыс параметрлерін табуға арналған өрнек болады Электр өрісінің потенциалы – скалярлық шама, өрістің берілген нүктесіндегі потенциалық энергияның, сыншы зарядқа қатынасы 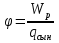 . . 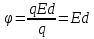 .Бұдан потенциал өрістің энергетикалық сипаттамасын беретін физикалық шама екенін көреміз. Өрістің күштік сипаттамасы кернеулік және оның энергетикалық сипаттамасы – потенциалдың арасында электростатикалық өрістің потенциалдығына негізделген байланыс бар. Потенциалды күш өрісінде потенциалдық энергия мен күш арасындағы байланыс мына түрде берілген .Бұдан потенциал өрістің энергетикалық сипаттамасын беретін физикалық шама екенін көреміз. Өрістің күштік сипаттамасы кернеулік және оның энергетикалық сипаттамасы – потенциалдың арасында электростатикалық өрістің потенциалдығына негізделген байланыс бар. Потенциалды күш өрісінде потенциалдық энергия мен күш арасындағы байланыс мына түрде берілген 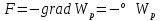 .мұнд. .мұнд. 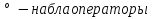 , оның түрі , оның түрі 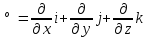 , осыдан , осыдан 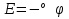 . Мұндағы «минус» таңбасы Е векторының бағыты әрқашан да потенциалдың кемуіне қарай бағытталғандығын көрсетеді. . Мұндағы «минус» таңбасы Е векторының бағыты әрқашан да потенциалдың кемуіне қарай бағытталғандығын көрсетеді.Нүктелік заряд потенциялының формуласы 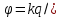 Er. Er.Потенциялдар айырмасын өлшейтін құрал-электрометр деп аталады. Потенциал[1] (потенциалдық функция) — физикалық күш өрістерінің кең көлемді тобын (электрлік, гравитациялық, т.б.) және физикалық шамалардың вектормен көрсетілген өрістерін (сұйықтық жылдамдығының өрісі, т.б.) сипаттайтын ұғым. Әрбір векторлық шама а өзінің потенциалының градиентіне тең: а=gradj. Мұндай жағдайда векторлық өрісті потенциалдық деп атайды. Потенциал векторлық өрісті сипаттау үшін көмекші функция ретінде енгізіледі. Термодинамикада потенциал берілген жүйе күйін сипаттаушы макропараметрлерге байланысты функция ретінде қарастырылады. Потенциал арқылы термодинам. жүйенің барлық қасиетін анықтауға болады. Физикада потенциал ұғымының басқа мағынасы да бар. Мысалы, электр өрісінде ол бірлік зарядты электр өрісінің берілген бір нүктесінен шексіздікке тасуға кеткен жұмысына тең. Потенциал(Педагогика) - қандай да болсын міндетті шешу үшін, белгілі мақсатқа жету үшін пайдаланылуы мүмкін қайнар-көздер, мүмкіндіктер, құралдар, қорлар, белгілі бір саладағы жеке тұлғаның, қоғамның, мемлекеттің мүмкіндіктері.[2] Векторлық потенциал - құйынды векторлық өрісті сипаттауға арналып қолданылатын векторлық функция.[1] векторный потенциал — это векторное поле, ротор которого равен заданному векторному полю. Он аналогичен скалярному потенциалу, который определяется как скалярное поле, градиент которого равен заданному векторному полю. Формально, если v — векторное поле, векторным потенциалом называется векторное поле A такое, что Если A является векторным потенциалом для поля v, то из тождества (дивергенция ротора равна нулю) следует то есть v должно быть соленоидальным векторным полем. Векторный потенциал в физике[править | править вики-текст] Основная статья: Векторный потенциал электромагнитного поля Уравнения Максвелла[править | править вики-текст] Одним из способов записи уравнений Максвелла является формулировка в терминах векторного и скалярного потенциалов. Векторный потенциал вводится таким образом, что При этом уравнение удовлетворяется автоматически. Подстановка выражения для в приводит к уравнению согласно которому, так же как и в электростатике вводится скалярный потенциал. Однако теперь в вносят вклад и скалярный и векторный потенциал: Из уравнения Используя равенство |
