1. Электрмагниттік рекеттесу, оны сипаттамалары. Классикалы электрдинамиканы пні жне дістері, баса физика пндері арасындаы орны
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
Скалярный потенциал векторного поля (чаще просто потенциал векторного поля) — это скалярная функция такая, что во всех точках области определения поля где обозначает градиент . В физике обычно потенциалом называют величину, противоположную по знаку (потенциал силы, потенциал электрического поля). 25. Электрмагниттік өрістің энергия ағынының тығыздығы және энергиясының тығыздығы.. Электромагниттік толқындарды анықтау мүмкіндігі, оларды энергияны тасымалдайтынын көрсетеді. Элмгнттк толқындар энерг.-ң w көл.-к тығ.-ғы, w(эл.) электр w(м) магниттік өрістердің көл.-к тығыздығынан қалыптасады: w = w(эл)+w(эл)= (ε0ε)E²/2 + μ0μH²/2, w(эл)=W/V=ED/2 ε0εE= μ0μH² осыны ескере отырып , уақыттың әрбір мезетіндегі эл. ж\е маг.-к өрістер энерг.-ң көлемдік тғздқнң бірдейлігін аламыз, яғни w(эл)=w(м). Сондықтан былай болады: w=2 w(эл)= ε0ε E²= 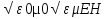 . .Энергияның тығыздығын ортадағы толқындардың таралу жылд.-на көбейтіп, энергия ағыны тығыздығының модулін аламыз: S=wv=EH, өйткені Е ж/e Н векторлары өзара перпенд.-р және толқындардың таралу бағытымен оң бұрандалық жүйені құрайды, сондықтан векторлар [ЕН] бағыты, энергияларды тасымалдау бағытымен сәйкес келеді, ал бұл вектордың модулі ЕН-ге тең. Элмгнттк энергия ағынының тығыздық векторы Умов-Поитинг векторы деп аталады: S=[EH] 26. Идеал біртекті диэлектриктегі электрмагниттік толқындық теңдеу. Жазық монохромат толқындар, олардың сипаттамалары. электрмагниттік толқындар–көлденең толқындар. айнымалы электр өрісінің кернеулігі 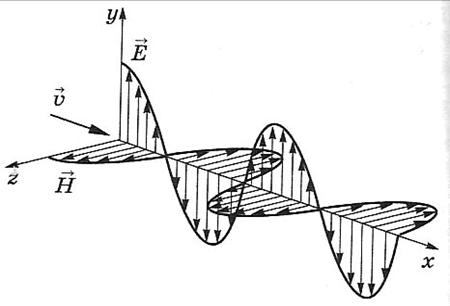 таралу жылдамдығы вектор 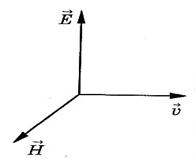 ына перпендикуляр (83-сурет). электрмагниттік толқында және векторлары бірдей фазада тербеледі. олардың лездік мәндері кез келген нүктеде мына қатынаспен байланысқан: мұндағы және үшін толқындық теңдеулер: мұндағы толқынның электр өрісі кернеулігінің амплитудасы; толқынның магнит өрісі кернеулігінің амплитудасы; тербелістердің x=0 координатқа сәйкес бастапқы фазалары. 27: Өткізгіш ортадағы электрмагниттік толқындар 25-26 да жауабы 28. Контурдағы мәжбүр электрмагниттік тербелістердің дифференциалдық теңдеуі және оның шешімі. Сыртқы периодты өзгеретіін күштердің әсерімен немесе сыртқы периодты өзгеретін ЭҚКның әсерінен туындайтын тербеліс- мәжбүр эектромагниттік тербеліс деп аталады. Мәжбүр тербеліс белгіленген режимде ω жиілікпен тербеледі, фаза мен амплитудаға тәуелді. Электромагниттік тербеліс үшін 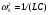 және и және и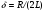 ескере отырып, ескере отырып, 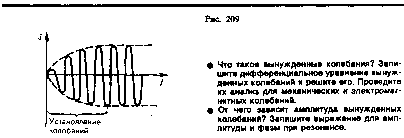 Т бойыншы дифференциалдай отырып, орнатылған тербеліс кезіндегі контурдағы токтыы есеептеййміз: 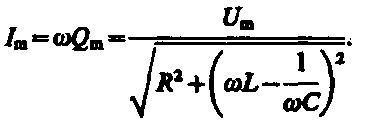 Бұл формуланы келесідей жазуға болады: Мұндағы = – /2 Бұл формулада ток фаза бойынша артта қалатын болса (>0), L>1/(С), ал керісінше болса (<0), если L<1/(С). 29. Контур элементтеріндегі кернеулер және тізбектегі ток күші үшін резонанстық қисықтар және олардың талдамы. Контурдың сапалылығы. Резонанс (лат. resono, фр. resonance — үн қосу, дыбыс қайтару) — периодты түрде сырттан әсер етуші күштің жиілігі тербелмелі жүйенің меншікті жиілігіне жақындағанда сол тербелмелі жүйедегі еріксіз тербелістер амплитудасының күрт арту құбылысы; мәжбүр етуші күштің жиілігі жүйе тербелісінің меншікті жиілігіне жуықтаған кезде жүйедегі мәжбүр тербеліс амплитудасының кенеттен артып кету кұбылысы.[1] Резонансты алғаш рет механика және акустикалық құбылыс ретінде италиян ғалым Г.Галилей, ал электр-магниттік жүйелерде, мысалы, тербелмелі контур арқылы ағылшын ғалымы Дж.Максвелл (1831 — 1879) қарастырған (1868). Жүйеге гармондық сыртқы күш (F) әсер еткенде массасы m-ге тең дененің қозғалыс теңдеуі мына түрде жазылады: мұндағы F0 — сыртқы күштің амплитудасы, v — сыртқы әсердің жиілігі, х — ауытқу, — масса жылдамдығы, a— масса үдеуі, b — үйкеліс коэфф., k — қатаңдық коэфф. Бұл теңдеудің шешуі болады. Мәжбүрлеуші күштің жиілігі тербелмелі жүйенің жиілігіне жақындаған сайын тербеліс амплитудасының қалай өсетіні осы формуладан айқын көрінеді. 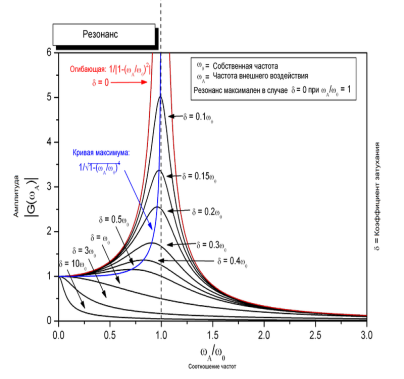 30.Реактивті және толық кедергі. Айнымалы ток тізбегі үшін Ом заңы Бір-біріне тізбектей жалғанған индуктивтігі катушкадан, сыйымдылығы конденсатордан және кедергісі резистордан тұратын тізбектің қысқыштарына 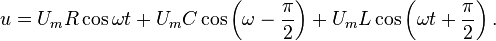 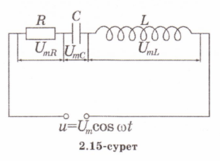 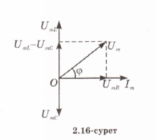 Түсірілген кернеудің амплитудасын векторлардың қосындысы ретінде табуға болады, яғни Түсірілген кернеудің амплитудасын векторлардың қосындысы ретінде табуға болады, яғни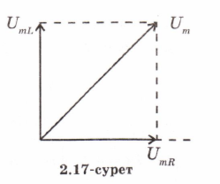 Егер (2.15) пен (2.16) өрнектерінде яғни деп алсақ, соңғы екі формула шығады. Олай болса, тізбекте конденсатор жоқ болса, сыйымдылық нөлге емес, шексіздікке тең екен. Шынында да, егер тізбектегі конденсатордың астарларын бір-біріне шексіз жақындатса, конденсаторды жоқ деп есептеуге болады. Ал жазық конденсатордың сыйымдылығы Егер (2.15) пен (2.16) өрнектерінде яғни деп алсақ, соңғы екі формула шығады. Олай болса, тізбекте конденсатор жоқ болса, сыйымдылық нөлге емес, шексіздікке тең екен. Шынында да, егер тізбектегі конденсатордың астарларын бір-біріне шексіз жақындатса, конденсаторды жоқ деп есептеуге болады. Ал жазық конденсатордың сыйымдылығы Генератордан алынатын энергия тек активті кедергіде ғана жылу энергиясы түрінде бөлініп шығады. Реактивті кедергіде энергияжұтылмайды. Реактивті кедергіде периодты түрде электр өрісінің энергиясы магнит өрісінің энергиясына айналып, түрленіп отырады. Периодтың бірінші ширегінде, конденсатор зарядталып жатқанда энергия тізбекке электр өрісінің энергиясы түрінде түсіп, жинақталады. Ал периодтың келесі ширегінде, конденсатор разрядталып жатканда, энергия қайтадан магнит өрісінің энергиясы түрінде желіге қайтарылады.[2] Тагы да R=p*l/S - ке тең болады. 31.Кернеу резонансы. Резонанстық жиілік. Айнымалы ток тізбегінің толық кедергісі 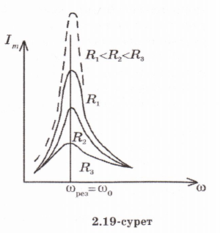 2.19-суретте 32.Айнымалы ток тізбегіндегі қуат. Қуат коэффициенті. Ток күшінің және кернеудің әсерлік мәндері. Айнымалы ток тізбегінде берілген уақыт мезетіндегі қуат ток күші мен кернеудің лездік мәндерінің көбейтіндісіне тең. Бұл өрнекті түрлендіріп Бізге бір период ішіндегі орташа қуатты анықтау керек. Ол үшін уақытқа тәуелді тригонометриялық функциялардың орташа мәндерін табайық: Олай болса, қуатты анықтайтын өрнектегі екінші қосылғыштың орташа мәні нөлге тең. Сонымен, айнымалы ток тізбегінде орташа қуат: Бұл теңдеуге ток пен кернеудің әсерлік мәндерін қойып, ыңғайлы болу үшін әсерлік мәндердің индексін жазбай және деп белгілесек, шығады. (2.18) мен (2.19) өрнектеріндегі шамасы қуат коэффициенті деп аталады. Осы өрнек айнымалы токтың қуаты тек ток күші мен кернеуге ғана емес, сонымен қатар олардың тербеліс фазаларының айырымына да тәуелді екенін көрсетеді. Егер тізбектегі реактивті кедергі болса, , онда , яғни бұрыннан белгілі тұрақты токтың қуатының формуласын аламыз. Ал тізбекте активті кедергі жоқ болса, |
