теплофизика. 1. Элементарные и сложные виды теплообмена
 Скачать 3.23 Mb. Скачать 3.23 Mb.
|
|
8. Местный и средний коэффициенты теплоотдачи. тепловой поток прямо пропорционален разности температур стенки и жидкости и площади поверхности теплообмена. Коэффициент пропорциональности или Величина коэффициента теплоотдачи зависит от большого числа различных факторов: а) физических свойств жидкости ; б) скорости движения жидкости ; в) формы, размеров и ориентации в пространстве поверхности теплообмена; г) величины температурного напора, направления теплообмена и т.п. Поэтому его теоретическое определение в большинстве случаев невозможно. Выражения (1)-(3) позволяют опытным путем определить средний коэффициент теплоотдачи посредством измерения величин Q, F, +то есть средний коэффициент теплоотдачи численно равен тепловому потоку, передаваемому через единицу поверхности теплообмена при единичном температурном напоре (1 оС или 1 К). Локальные коэффициенты характеризуют теплоотдачу в окрестности заданной точки (x) и входят в состав локального уравнения теплоотдачи: или локальные коэффициенты теплоотдачи в принципе могут быть найдены опытным путем посредством измерения величин На практике вдоль поверхности выделяют необходимое количество конечных, но достаточно малых участков и производят измерения для каждого i-го участка поверхности: 9. Коэффициент радиационно-конвективного теплообмена Сложный вид передачи тепла в результате параллельного и одновременного протекания процессов теплоотдачи и излучения называют - радиационно-конвективный теплообмен. Результат совместного действия простых процессов переноса теплоты (конвекция, излучение и теплопроводность), как правило, приписывается одному из них, который считается главным. Влияние остальных явлений учитывается количественно коэффициентом пропорциональности. Если в качестве главного принята теплоотдача то, можно записать: +где Выражение для расчета значения где где +Последнее уравнение представим в виде: тогда получим Если в качестве главного принять перенос теплоты излучением, получим следующее выражение для расчета степени черноты, учитывающей конвективную составляющую переноса теплоты: 10. Массообмен. Под массообменом (mass exchange) понимают перенос вещества, возникающий в жидкостях и газах при их конвективном макроперемешивании, за счет молекулярной диффузии, а также за счет простого перемешивания. Общий предмет массообмена можно подразделить на четыре широкие области, представляющие особый интерес в практике: • молекулярная диффузия в неподвижной среде; • диффузия в жидкостях при ламинарном течении; • турбулентная диффузия (перемешивание в свободном турбулентном потоке); • массообмен между двумя фазами Молекулярная диффузия (molecular diffusion) - это процесс выравнивания концентраций (плотностей) двух веществ при их смешении друг с другом. Взаимное проникновение веществ является результатом хаотического движения их частиц. Каждое вещество диффундирует из зон с большой концентрацией в зоны с малой концентрацией вещества. Термодиффузия (thermodiffusion). Молекулярная диффузия может происходить под воздействием концентрационных, температурных градиентов или градиентов давления, а также в случае, когда на смесь накладывается направленный внешний электрический или иной потенциал. Конвективный массообмен (convective mass exchange) - это макроперенос вещества, возникающий в жидкостях и газах при их конвективном макроперемешивании. Таким образом, перенос вещества происходит не только под воздействием градиента концентрации, но и совместно с движущейся жидкостью. Такой процесс обычно называют конвекцией. Аналогично закону теплоотдачи Ньютона закон массоотдачи записывают в виде  Многофазный массообмен (multiphase mass exchange) - это перенос вещества между двумя фазами через межфазную границу. 11. Краевые условия (условия однозначности). Так как дифференциальное уравнение теплопроводности выведено на основе самого общего закона термодинамики, то оно описывает явление теплопроводности в самом общем виде, т.е. оно описывает целый класс явлений теплопроводности. Чтобы из бесчисленного количества выделить конкретно рассматриваемый процесс теплопроводности и дать его полное математическое описание, к дифференциальному уравнению необходимо присоединить математическое описание всех частных особенностей рассматриваемого процесса. Эти частные особенности, которые совместно с дифференциальным уравнением дают полное математическое описание конкретного процесса теплопроводности, называются условиями однозначности или краевыми условиями. Условия однозначности включают в себя: 1. Геометрические условия, которыми задаются форма и линейные размеры тела. 2. Физические условия, которыми задаются физические параметры тела (λ, с, ρ и др.) и может быть задан закон распределения внутренних источников теплоты. 3. Начальные условия, характеризующие распределение температуры в изучаемом теле в начальный момент времени. Начальные условия необходимы лишь при рассмотрении нестационарных процессов и состоят в задании закона распределения температуры внутри тела в начальный момент времени. В общем случае начальные условия аналитически могут быть записаны следующим образом (при τ = 0): t = ƒ (x, y, z) При равномерном распределении температуры в теле начальные условия упрощаются (при τ = 0): t = t0 = const 4. Граничные условия, характеризующие взаимодействие рассматриваемого тела с окружающей средой. Граничные условия могут быть заданы четырьмя способами. I) Граничные условия I рода. Задается распределение температуры на поверхности тела для каждого момента времени 2) Граничные условия П рода. В этом случае задаются значения плотности теплового потока для каждой точки поверхности тела и любого момента времени. 3) Граничные условия Ш рода. В этом случае задается температура окружающей среды (жидкости) tж и закон теплообмена между поверхностью тела и окружающей средой. Для описания процесса теплообмена между поверхностью тела и окружающей средой используется закон Ньютона-Рихмана 4) Граничные условия IV рода формируются на основании равенства тепловых потоков, проходящих через поверхность соприкосновения тела с окружающей средой или поверхность соприкосновения трердых тел, по закону теплопроводности 12. Четыре рода граничных условий. Для решения дифференциального уравнения необходимы краевые условия (условия однозначности) при решении задач теплопроводности. Краевые условия подразделяются: Геометрические – ими задаются форма и размеры объекта; Физические условия однозначности – задаются значения теплофизических характеристик вещества 1. Временные или начальные условия – для решения нестационарных задач. Задается закон распределения температуры в начальный момент времени. 4. Граничные условия – условия на границе раздела сред то есть на поверхности объекта. Подразделяются на граничные условия четырех родов. Граничные условия. · Граничными условиями первого рода задается закон распределения температуры по поверхности объекта в любой точке поверхности и в любой момент времени. · Граничные условия второго рода – определяют значения плотности теплового потока на поверхности объекта в любой точке и в любой момент времени. · Граничные условия третьего рода – определяют температуру жидкости омывающей поверхность или закон ее изменения и условия теплообмена на границах раздела сред. Должна быть задана температура и вид теплообмена (tж, tc, a…). · Граничные условия четвертого рода – условия на границе раздела двух твердых тел. Теплота, подведенная к поверхности одного тела, передается полностью другому телу, имеющему другие характеристики. Совокупность дифференциального уравнения теплопроводности и условия однозначности представляют собой полную математическую формулировку задачи. 13. Краевые условия для системы уравнений, описывающих теплоотдачу Основное дифференциальное уравнение теплопроводности характеризует пространственно-временное изменение температуры в любой точке поля, объединяя все без исключения явления теплопроводности независимо от геометрической формы тела, его физических свойств и условий взаимодействия с окружающей средой. Краевые граничные условия связаны с взаимодействием изучаемого тела с окружающей средой (например, распределение температур на поверхности тела для каждого момента времени). Граничные краевые условия в свою очередь могут быть заданы тремя способами: Граничное условие первого рода задается распределением температур по поверхности тела для любого момента времени. Граничное условие второго рода задается тепловым потоком в каждой точке поверхности тела для каждого момента времени. Граничное условие третьего рода заключается в задании температуры среды, окружающей изучаемое тело, и закона теплоотдачи между поверхностями и окружающей средой.  14. Основы теории подобия физических явлений Подобными называются физические явления, протекающие в геометрически подобных системах, если у них во всех сходственных точках в сходственные моменты времени отношения одноименных величин есть постоянные числа. Эти постоянные числа называются константами подобия. Так работа двух экземпляров идентичных по принципу действия и конструкции машин может быть признана подобной если основные характеристики будут отвечать условиям: Явления, описываемые одинаковыми физическими уравнениями (или системами уравнений), но имеющие различную физическую природу, называют аналогичными В процессе теоретических исследований всегда можно вывести безразмерный коэффициент, характеризующий соотношение между параметрами машины, имеющие одинаковые размерности. Эти безразмерные коэффициенты можно рассматривать как константы подобия. Константы подобия это такие безразмерные соотношения параметров машины которые у подобных машин в сходственных точках имеют численно одинаковые значения. Эти безразмерные соотношения называют числами подобия. Основы теории подобия составляют 3 теоремы. Первая теорема вытекает из формулировки понятия числа подобия. Из этого понятия следует: у подобных явлений (машин) одноименные числа подобия одинаковы. Вторая теорема гласит: если физическое явление описывается системой дифференциальных уравнений, то интеграл этой системы можно представить как функцию чисел подобия полученных из дифференциальных уравнений. Третья теорема определяет минимальные условия, при котором машины или явления можно признать подобными Теорема звучит так: подобны те явления машины, условия однозначности которых подобны. 15. Роль теории подобия в исследовании процессов теплообмена Исходные дифференциальные уравнения и их решение, а также результаты экспериментального изучения конвективного теплообмена целесообразно представлять в виде зависимостей между безразмерными комплексами – числами подобия. Эти безразмерные (отвлеченные) чис-ла составляются из размерных физических параметров, определяющих явление конвективного теплообмена. Произведение чисел подобия и частное от их деления также представляют собой числа подобия. Приведение математического описания процесса конвективного теплообмена и расчетных соотношений к безразмерному виду позволяет выявить условия подобия и сопоставимости процессов, сокращает число переменных и постоянных величин, определяющих процесс; в случае экспериментального исследования позволяет свести к минимуму число величин, которые необходимо варьировать в опытах, указывает компактный и рациональный способ обобщения экспериментальных данных; дает возможность не решая исходную систему дифферен-циальных уравнений, анализировать предельные случаи и установить числа подобия, которые характеризуют наиболее существенные особенности процессов теплоотдачи в данных конкретных условиях. Эти числа подобия в общем случае являются мерой относительного влияния действующих сил и процессов переноса (потока импульса, энергии, массы) на течение жидкости и теплообмен. Так, для стацио-нарных процессов конвективного теплообмена в однофазной несжимаемой жидкости с постоянными (кроме плотности) физическими свойствами характерны следующие безразмерные числа подобия: число Нуссельта Nu = αℓ/λ, (3.15) характеризующее конвективный теплообмен между теплоносителем и поверхностью твердого тела. Число Нуссельта определяется теми же величинами, что и число Био (формула 2.61), но в число Nu входит коэффициент теплопроводности теплоносителя (жидкости или газа), а в число Bi – коэффициент теплопроводности твердого тела; число Рейнольдса Re = wℓρ/μ = wℓ/ν, (3.16) характеризующее соотношение сил инерции и сил вязкости в потоке теплоносителя (жидкости или газа); число Прандтля Pr = μcp/λ = ν/α, (3.17) характеризующее физические свойства теплоносителя; 16. Понятие о подобии физических явлений, константы и числа подобия. Подобными называют явления, для которых подобны условия однозначности. Под условиями однозначности принято понимать подобие геометрических форм,физических свойств среды и тела, начальных и граничных условий,т.е. условий, обусловливающих однозначность поведения системы.Условия однозначности могут задаваться в виде численных значений или функциональной зависимости. Граничными называют условия, характеризующие взаимодействие системы с окружающей средой. Начальными называют условия, характеризующие состояние системы в начальный момент времени. 17. Способы получения чисел подобия. Для получения чисел подобия необходимо воспользоваться системой диф. уравнений конвективного теплообмена: 1) Диф. уравнение теплоотдачи. Из него получено число Нуссельта (Nu). 2) Диф. уравнение энергии. В результате его исследования получены числа F0–число Фурье, Pe– число Пекле. 3) Уравнение движения жидкости (Навье–Стокса). Получены следующие числа: – число гомохромности – число Эйлера 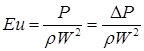 . .– число Рейнольдса Если рассмотреть уравнение Навье–Стокса в случае свободного движения (при отсутствии вынужденного) то получим число Гросгоффа 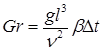 . .Подобие процессов теплоотдачи в самом общем случае будет соблюдаться при равенстве семи чисел подобия. Решение системы дифференциальных уравнений конвективного теплообмена в самом общем случае можно представить в виде: 18. Коэффициенты теплопроводности различных тел. Теплопроводность тела означает его способность проводить тепло. Если в разных местах тела температура различна, то возникает поток тепла из мест более нагретых в места менее нагретые, продолжающийся до тех пор, пока температура во всем теле не выровняется. Теплопроводность тела количественно оценивается значением коэффициента теплопроводности l, который определяет скорость передачи тепла (количество переданной теплоты Q за единицу времени t, т.е. Q/t) от более нагретых к менее нагретым участкам в единице объема тела V при разности температур между участками DТ = 1 К, т.е. (6). Значения коэффициентов теплопроводности приводятся в справочниках по теплофизическим свойствам веществ. Наибольшей теплопроводностью обладает легкий газ — водород. При комнатных условиях коэффициент теплопроводности водорода λ = 0,2 Вт/(м·К). У более тяжелых газов теплопроводность меньше — у воздуха λ = 0,025 Вт/(м·К), у диоксида углерода λ = 0,02 Вт/(м·К). Наибольшим коэффициентом теплопроводности обладают чистые серебро и медь: λ = 400 Вт/(м·К). Для углеродистых сталей λ = 50 Вт/(м·К). У жидкостей коэффициент теплопроводности, как правило, меньше 1 Вт/(м·К). Вода является одним из лучших жидких проводников теплоты, для нее λ = 0,6 Вт/(м·К). Коэффициент теплопроводности неметаллических твердых материалов обычно ниже 10 Вт/(м·К). Пористые материалы – пробка, различные волокнистые наполнители типа органической ваты – обладают наименьшими коэффициентами теплопроводности λ<0,25 Вт/(м·К), приближающимся при малой плотности набивки к коэффициенту теплопроводности воздуха, наполняющего поры. 19. Теплопроводность простых газов и химически реагирующих смесей, влияние температуры и давления на теплопроводность газов 20. Теплопроводность и теплопередача при одномерном температурном поле. Температурным полем называется совокупность значений температуры в данный момент времени во всех точках изучаемого пространства. В общем случае уравнение температурного поля имеет вид: t=F(x, y, z, τ), (1.1) где t – температура среды; x,y,z – координаты точки среды; τ – время. Температурное поле, изменяющееся во времени, называется нестационарным, а температурное поле, не изменяющееся во времени, - стационарным 21. Расчетные соотношения для плоской и цилиндрической стенок. В стационарном режиме теплопроводности температурное поле не изменяется во времени, т.е. . В этом случае дифференциальное уравнение теплопроводности для тел простейшей формы при допущении независимости физических свойств тела от температуры принимает вид 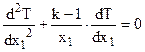 или в дивергентной форме или в дивергентной форме 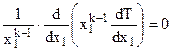 , ,где x1 – координата, м; k – коэффициент формы тела. Подставляя в последнее уравнение значения коэффициента формы тела и обозначение координаты для тел простейшей формы, получим а) бесконечная пластина или плоская стенка (k = 1, x1 = x) 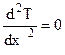 ; ;б) бесконечный цилиндр (k = 2, x1 = r) Плоская стенка Решая дифференциальное уравнение теплопроводности для плоской стенки при следующих условиях однозначности: — толщина стенки равна δ, м; — коэффициент теплопроводности стенки не зависит от температуры и равен λ Вт/(м·К); — внутренние источники (стоки) теплоты в стенке отсутствуют, т.е. ; — на обеих поверхностях плоской стенки задано значение температуры (ГУ I рода) 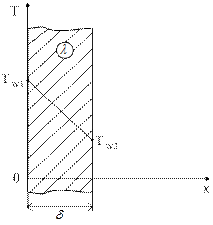 Рис.2.4. Стационарное температурное поле в плоской стенке Подставляя значение постоянных интегрирования в общее решение находится температурное поле Зная температурное поле, несложно рассчитать плотность теплового потока в плоской стенке, воспользовавшись законом Фурье и получим 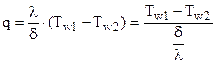 , ,где – тепловая проводимость плоской стенки, Вт/(м2×К); – термическое сопротивление теплопроводности плоской стенки, (м2×К)/Вт. Плотность теплового потока для плоской стенки, состоящей из n слоев, рассчитывается по формуле:  . .где – перепад температур на i-ом слое многослойной стенки; – термическое сопротивление теплопроводности i-го слоя многослойной стенки. Цилиндрическая стенка Решая дифференциальное уравнение теплопроводности для цилиндрической стенки при следующих условиях однозначности: — внутренний и наружный радиусы цилиндрической стенки равны r1 и r2 ,м; — коэффициент теплопроводности стенки не зависит от температуры и равен λ Вт/(м·К); — внутренние источники (стоки) теплоты в стенке отсутствуют, т.е. ; — на обеих поверхностях цилиндрической стенки задано значение температуры (ГУ I рода) Формула изменения температурного поля в цилиндрической стенке 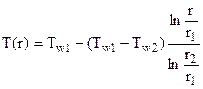  Рис.2.5. Стационарное температурное поле в цилиндрической стенке расчетах теплопроводности через цилиндрическую стенку используют тепловой поток, отнесенный к длине цилиндрической стенки – линейную плотность теплового потока где В общем случае для любого слоя i – го многослойной цилиндрической стенки можем записать 22. Теплопроводность тел с внутренними источниками теплоты. Для однородной плоской стенки с внутренним источником теплоты поверхностная плотность теплового потока qx, Вт/м2.
Температура 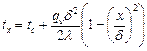 . (1.24) . (1.24)С учетом зависимости теплопроводности l от температуры  . (1.25) . (1.25)Для круглого стержня с внутренним источником теплоты (рисунок 1.4) поверхностная плотность теплого потока qr изменяется пропорционально радиусу r: Температура 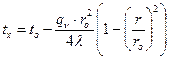 , (1.27) , (1.27)где to – температура при r=0. Перепад температуры по радиусу стержня: где qe=qn·p· . С учетом зависимости теплопроводности l от температуры  . (1.29) . (1.29)
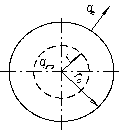
С учетом зависимости теплопроводности l от температуры 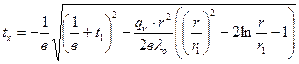 . (1.33) . (1.33)б) теплота отводится через внутреннюю поверхность цилиндра 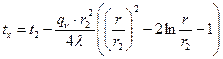 ; (1.34) ; (1.34)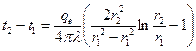 . (1.35) . (1.35)С учетом зависимости теплопроводности l от температуры 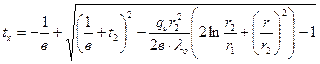 . (1.36) . (1.36)23. Контактное термическое сопротивление. На реальных поверхностях всегда имеются микроскопические неровности. Поэтому соприкосновение тел происходит не по всей поверхности, а лишь по отдельным небольшим зонам, остальные участки поверхностей контактирующих тел разделены прослойкой газа. Это приводит к появлению теплового сопротивления в месте соприкосновения поверхностей 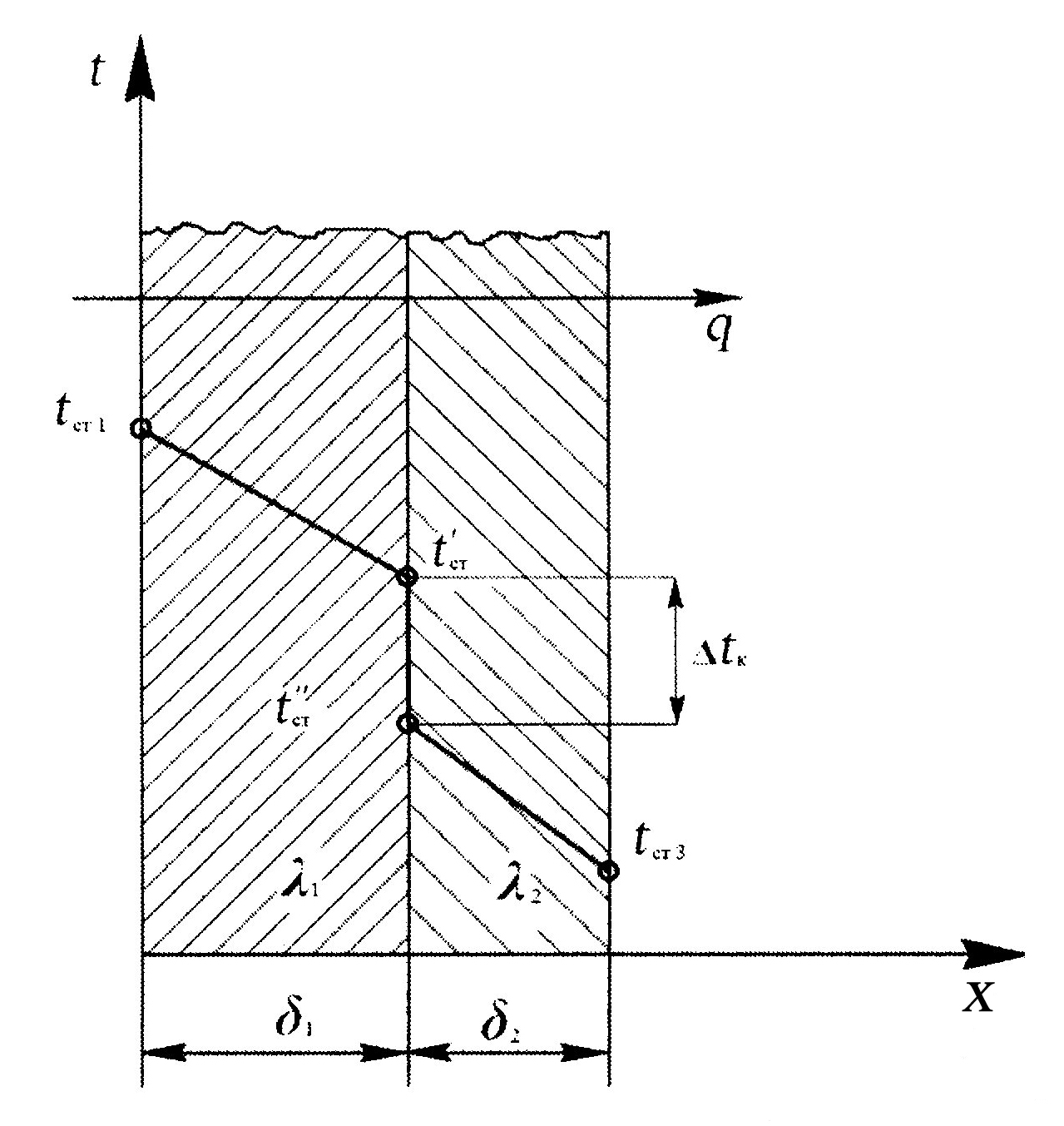 Рис. 9.10. К объяснению контактного теплового сопротивления Этот скачок температуры (∆tк) связан с плотностью теплового потока q и контактным тепловым сопротивлением (Rк) следующим уравнением: 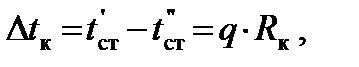 (9.42) (9.42)где , – температуры контактирующих поверхностей; Rк – контактное тепловое сопротивление. Величина Rк зависит от природы, чистоты обработки (рис. 9.11.) и твердости контактирующих поверхностей. Для плоской двухслойной стенки уравнение теплопроводности с учётом сопротивления контакта имеет вид: 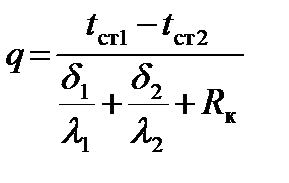 . (9.43) . (9.43)Значения Rк определяют по опытным данным или расчётным путём с помощью полуэмпирических методов. 24. Факторы, определяющие интенсивность процесса теплоотдачи На интенсивность теплоотдачи (при данном температурном напоре) влияют: - природа возникновения движения; - скорость и степень турбулентности набегающего потока; - режим течения в пограничном слое; - температура и физические свойства теплоносителя; - форма, размеры и шероховатость поверхности обтекаемого тела и т.д. Природа возникновения движения. Движение теплоносителя может быть вынужденным или свободным. Вынужденное движение возникает за счет внешних для данного процесса причин (движение летательного аппарата относительно воздуха; течение, обусловленное разностью давлений, создаваемой насосом, эжектором или компрессором, и др.). Свободным называется движение, возникающее за счет неоднородного распределения массовых сил в объеме теплоносителя вследствие разности плотностей холодных и горячих его частиц. Свободное движение называют также свободной конвекцией. Степень турбулентности набегающего потока. Степень турбулентности набегающего потока влияет на характер развития и структуру пограничного слоя (условия перехода ламинарного пограничного слоя в турбулентный и уровень турбулентности в турбулентном пограничном слое). Физические свойства теплоносителя. Интенсивность конвективного теплообмена зависит от теплопроводности, теплоемкости, вязкости и плотности теплоносителя. Влияние коэффициента теплопроводности l на интенсивность конвективного теплообмена связано прежде всего с ламинарной частью пограничного слоя, и особенно его пристенными слоями, где скорость потока близка к нулю и теплота передаётся в основном за счёт теплопроводности. Влияние теплоёмкости с (для газов - cp) связано с тем, что при одинаковых условиях течения теплоноситель с большей теплоёмкостью переносит большее количество теплоты. Вязкость теплоносителя оказывает влияние на толщину пограничного слоя и на интенсивность турбулентного перемешивания в нём. При прочих равных условиях увеличение вязкости приводит к образованию более толстого пограничного слоя и ухудшению перемешивания в нём. Вязкость газов и жидкостей характеризуют коэффициентом динамической вязкости m, Па×с и коэффициентом кинематической вязкостиn, м2/с, которые связаны соотношением , где r, кг/м3 - плотность теплоносителя. Влияние плотности теплоносителя r на конвективный теплообмен проявляется через изменения массового расхода теплоносителя и коэффициента кинематической вязкости. Форма, размеры и шероховатость поверхности обтекаемого тела оказывают влияние на формирование пограничного слоя. 25. Обзор методов получения расчетных формул для оценки коэффициента теплоотдачи. Коэффициентом теплоотдачи называется физическая величина, которая характеризует интенсивность теплоотдачи при известном изменении температуры. в гидроаэродинамике Коэффициент  равен: равен: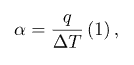 где q — плотность теплового потока, dT— температурный напор. Формула Ньютона-Рихмана Коэффициент теплоотдачи входит в выражение для потока тепла в веществе жидкой или газообразной среды с интенсивным изменением температуры при увеличении расстояния от охлаждаемого или нагреваемого объекта: где Q — количество теплоты, которая отводится от поверхности, имеющую площадь S, Tsr — температура вещества (жидкости, газа), Tpov — температура поверхности тела. Так как интенсивность теплообмена может изменяться при передвижении вдоль площади соприкосновения жидкого носителя с поверхностью твердого тела, вводят местный коэффициент теплоотдачи, который равен: 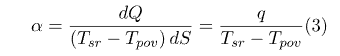 Дифференциальное уравнение теплоотдачи Дифференциальное уравнение теплоотдачи показывает связь между коэффициентом теплоотдачи и полем температур среды (жидкости или газа): 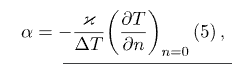 где  — градиент температуры, индекс n=0 значит то, что градиент берут на стенке. — градиент температуры, индекс n=0 значит то, что градиент берут на стенке.Критерий Нуссельта Критерий Нуссельта (Nu) является характеристикой теплообмена на границе между жидкостью и стеной: 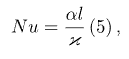 где l — характерный линейный размер, Лямбда — коэффициент теплопроводности жидкости. |

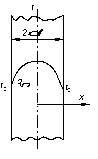
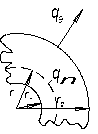
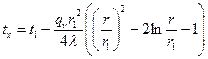 . (1.31) При r=r2
. (1.31) При r=r2 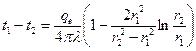 . (1.32)
. (1.32)