Дискретное преобразование Фурье
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
Дискретное преобразование Фурье Дискретное преобразование Фурье (в англоязычной литературе DFT, Discrete Fourier Transform) — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать частные дифференциальные уравнения и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Существуют многомерные дискретные преобразования Фурье. Преобразование Фурье (Fouriertransform)– это разложение функций на синусоиды (далее косинусные функции мы тоже называем синусоидами, т.к. они отличаются от «настоящих» синусоид только фазой). Существует несколько видов преобразования Фурье. 1. Непериодический непрерывный сигнал можно разложить в интеграл Фурье. 2. Периодический непрерывный сигнал можно разложить в бесконечный ряд Фурье. 3. Непериодический дискретный сигнал можно разложить в интеграл Фурье. 4. Периодический дискретный сигнал можно разложить в конечный ряд Фурье. Компьютер способен работать только с ограниченным объемом данных, следовательно, реально он способен вычислять только последний вид преобразования Фурье. Рассмотрим его подробнее. ДПФ вещественного сигнала Пусть дискретный сигнал x[n] имеет период N точек. В этом случае его можно представить в виде конечного ряда (т.е. линейной комбинации) дискретных синусоид: 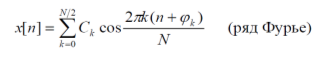 Эквивалентная запись (каждый косинус раскладываем на синус и косинус, но теперь без фазы): 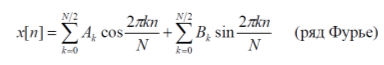 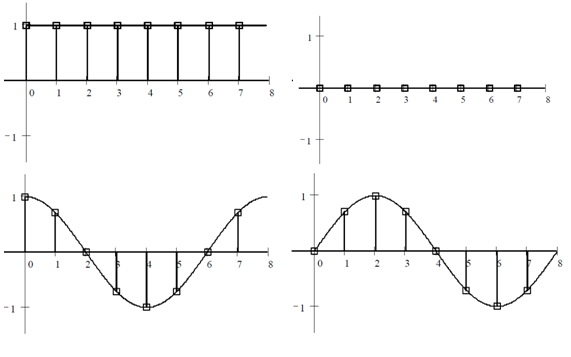 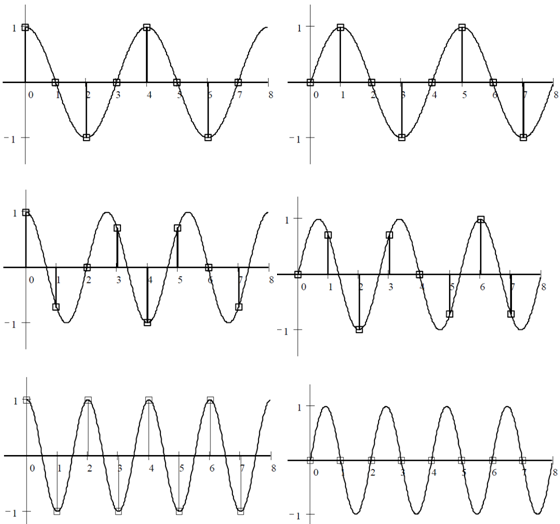 Рис. 1 - Базисные функции ряда Фурье для 8-точеченого дискретного сигнала. Слева – косинусы, справа – синусы. Частоты увеличиваются сверху вниз Базисные синусоиды имеют кратные частоты. Первый член ряда (k=0) – это константа, называемая постоянной составляющей (DC offset) сигнала. Самая первая синусоида (k=1) имеет такую частоту, что ее период совпадает с перио-дом самого исходного сигнала. Самая высокочастотная составляющая (k=N/2) имеет такую частоту, что ее период равен двум отсчетам. Коэффициенты 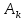 и и 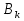 называются спектром сигнала (spectrum). Они показывают амплитуды синусоид, из которых состоит сигнал. Шаг по частоте между двумя соседними синусоидами из разложения Фурье называется частотным разрешением спектра. называются спектром сигнала (spectrum). Они показывают амплитуды синусоид, из которых состоит сигнал. Шаг по частоте между двумя соседними синусоидами из разложения Фурье называется частотным разрешением спектра.На рис. 1 показаны синусоиды, по которым происходит разложение дискретного сигнала из 8 точек. Каждая из синусоид состоит из 8 точек, то есть является обычным дискретным сигналом. Непрерывные синусоиды показаны на рисунке для наглядности. Как мы увидим далее, для каждого сигнала можно однозначно определить коэффициенты 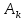 и и 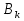 . .Зная эти коэффициенты, можно однозначно восстановить исходный сигнал, вычислив сумму ряда Фурье в каждой точке. Разложение сигнала на синусоиды (т.е. получение коэффициентов) называется прямым преобразованием Фурье. Обратный процесс – синтез сигнала по синусоидам – называется обратным преобразованием Фурье (inverseFouriertransform). Алгоритм обратного преобразования Фурье очевиден (он содержится в формуле ряда Фурье; для проведения синтеза нужно просто подставить в нее коэффициенты). Рассмотрим алгоритм прямого преобразования Фурье, т.е. нахождения коэффициентов 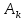 и и 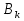 . .Система функций: 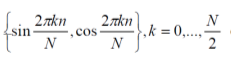 от аргумента n является ортогональным базисом в пространстве периодических дискретных сигналов с периодом N. Это значит, что для разложения по ней любого элемента пространства (сигнала) нужно посчитать скалярные произведения этого элемента со всеми функциями системы, и полученные коэффициенты нормировать. Тогда для исходного сигнала будет справедлива формула разложения по базису с коэффициентами 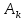 и и 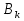 . .Итак, коэффициенты 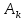 и и 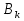 вычисляются как скалярные произведения (в непрерывном случае – интегралы от произведения функций, в дискретном случае – суммы от произведения дискретных сигналов): вычисляются как скалярные произведения (в непрерывном случае – интегралы от произведения функций, в дискретном случае – суммы от произведения дискретных сигналов):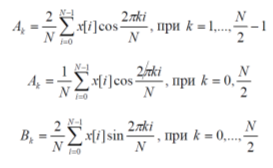 Возникает вопрос: почему в исходном сигнале N чисел, а описывается он с помощью N+2 коэффициентов? Вопрос разрешается следующим образом: коэффициенты 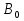 и и 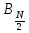 всегда равны нулю (т.к. соответствующие им «базисные» сигналы тождественно равны нулю в дискретных точках), и их можно отбросить при вычислении обратного и прямого преобразований Фурье. всегда равны нулю (т.к. соответствующие им «базисные» сигналы тождественно равны нулю в дискретных точках), и их можно отбросить при вычислении обратного и прямого преобразований Фурье.Итак, мы выяснили, что спектральное представление сигнала полностью эквивалентно самому сигналу. Между ними можно перемещаться, используя прямое и обратное преобразования Фурье. Алгоритм вычисления этих преобразований содержится в приведенных формулах. Комплексное ДПФ До сих пор мы рассматривали ДПФ от действительных сигналов. Обобщим теперь ДПФ на случай комплексных сигналов. Пусть x[n], n=0,…,N-1 – исходный комплексный сигнал, состоящий из N комплексных чисел. Обозначим X[k], k=0,…N-1 – его комплексный спектр, также состоящий из N комплексных чисел. Тогда справедливы следующие формулы прямого и обратного преобразований Фурье (здесь 1−=j): 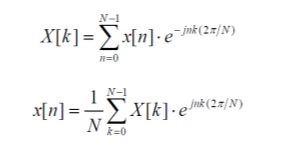 Если по этим формулам разложить в спектр действительный сигнал, то первые N/2+1 комплексных коэффициентов спектра будут совпадать со спектром «обычного» действительного ДПФ, представленным в «комплексном» виде, а остальные коэффициенты будут их симметричным отражением относительно половины частоты дискретизации. Для косинусных коэффициентов отражение четное, а для синусных – нечетное. Двумерное ДПФ Для изображений, представляющих собой двумерный сигнал, спектром является также двумерный сигнал. Базисные функции преобразования Фурье имеют вид 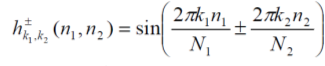 причем фазы также могут быть различны. На изображении каждая из этих базисных функций представляют собой волну определенной частоты, определенной ориентации и определенной фазы. Здесь N1xN2 – размер исходного сигнала, он же – размер спектра. k1 и k2 – это номера базисных функций (номера коэффициентов двумерного ДПФ, при которых эти функции находятся). Поскольку размер спектра равен размеру исходного сигнала, то k1 = 0,…,N1-1; k2 = 0,…,N2-1. n1 и n2 – переменные-аргументы базисных функций. Поскольку область определения базисных функций совпадает с областью определения сигнала, то n1 = 0,…,N1-1; n2 = 0,…,N2-1. Двумерное ДПФ (в комплексной форме) определяется следующими формулами (здесь x[n1,n2] - исходный сигнал, а X[k1,k2] – его спектр): 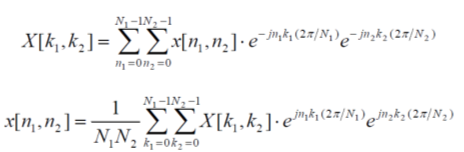 Непосредственное вычисление двумерного ДПФ по приведенным формулам требует огромных вычислительных затрат. Однако можно доказать, что двумерное ДПФ обладает свойством сеперабельности, т.е. его можно вычислить последовательно по двум измерениям. Для вычисления двумерного ДПФ достаточно вычислить одномерные комплексные ДПФ всех строк изображения, а затем вычислить в результирующем «изображении» одномерные комплексные ДПФ всех столбцов. При этом результаты всех одномерных комплексных ДПФ нужно записывать на место исходных данных для этих ДПФ. Например, при вычислении одномерного ДПФ первой строки изображения нужно результат ДПФ записать в первую строку этого изображения (он имеет тот же размер). Для этого нужно каждый «пиксель» хранить в виде комплексного числа. Ряды Фурье Разложению в ряды Фурье подвергаются периодические сигналы. Периодическую функцию любой формы, заданную на интервале одного периода Т = b-a и удовлетворяющую на этом интервале условиям Дирехле (ограниченная, кусочно-непрерывная, с конечным числом разрывов 1-го рода), можно представить в виде ряда Фурье: s(t) = где весовые коэффициенты Sn ряда определяются по формуле: Sn = (1/T) Ряд Фурье представляет собой ансамбль комплексных экспонент exp(jnDwt) с частотами, образующими арифметическую прогрессию. Функцию весовых коэффициентов S(nDw) принято называть комплексным спектром периодического сигнала или фурье-образом функции s(t). Спектр периодического сигнала является дискретной функцией, т.к. он определен только для целых значений n с шагом по частоте, обратным периоду: Dw = 2p/Т (или Df = 1/T). Первую частотную составляющую спектра при n = 1, равную w1 = 1Dw = 2p/T (или f1 = 1/T), называют основной частотой сигнала (первой гармоникой), остальные частоты дискретного спектра nDw при n>1 называют гармониками сигнала. Значения S(nDw) по положительным и отрицательным значениям n являются комплексно сопряженными. Шаг по частоте Dw между двумя соседними синусоидами называется частотным разрешением спектра. С чисто математических позиций множество функций exp(jnDwt), -< n < образует бесконечномерный базис линейного пространства L2[a,b] ортогональных синус-косинусных функций, а коэффициенты Sn по (2) представляют собой проекции сигнала s(t) на эти базисные функции. Соответственно, сигнал s(t) в форме ряда Фурье (1) – это бесконечномерный вектор в пространстве L2[a,b], точка с координатами Sn по базисным осям пространства exp(jnDwt). Коэффициенты Sn в (2) отображают функцию s(t) в новое пространство единственным образом. Если функция s(t) непрерывна, то ряд (1) сходится равномерно к s(t), при этом ошибка аппроксимации ||s(t)-sN(t)|| функции s(t) с усечением ряда (1) до ±N членов меньше ошибки аппроксимации любым другим рядом с тем же количеством членов. Если s(t) не является непрерывной (имеет разрывы), но конечна по энергии (квадратично интегрируема), то метрика ||s(t)-sN(t)|| стремится к нулю при N → ∞, при этом в точках разрыва сумма ряда стремится к (s(t+)+s(t-))/2. Подынтегральную функцию экспоненты в выражении (2) с использованием тождества Эйлера exp(±jwt) = cos(wt) ± jsin(wt) можно разложить на косинусную и синусную составляющие и выразить комплексный спектр в виде действительной и мнимой части: Sn = (1/T) An ≡ A(nDw)= (1/T) Bn ≡ B(nDw)= (1/T) На рис. 1 приведен пример периодического сигнала (прямоугольный импульс на интервале (1-3.3), повторяющийся с периодом Т=40) и форма действительной и мнимой части его спектра. Обратим внимание, что действительная часть спектра является четной относительно нуля функцией A(nDw) = A(-nDw), так как при вычислении значений A(nDw) по формуле (4) используется четная косинусная функция cos(nDwt) = cos(-nDwt). Мнимая часть спектра является нечетной функцией B(nDw) = -B(-nDw), так как для ее вычисления по (5) используется нечетная синусная функция sin(nDwt) = - sin(-nDwt). 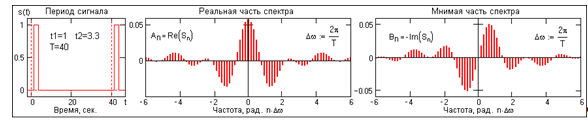 Рис. 2 - Сигнал и его комплексный спектр Комплексные числа дискретной функции (3) могут быть представлены в виде модулей и аргументов комплексной экспоненты, что дает следующую форму записи комплексного спектра: Sn = Rnexp(jjn), (3') Rn2 ≡ R2(nDw) = A2(nDw)+B2(nDw), jn ≡ j(nDw) = arctg(-B(nDw)/A(nDw)). Модуль спектра R(nDw) называют двусторонним спектром амплитуд или АЧХ - амплитудно-частотной характеристикой сигнала, а аргумент спектра (последовательность фазовых углов j(nDw)) - двусторонним спектром фаз или ФЧХ – фазочастотной характеристикой. Спектр амплитуд всегда представляет собой четную функцию: R(nDw) = R(-nDw), а спектр фаз нечетную: j(nDw) = -j(-nDw). Пример спектра в амплитудном и фазовом представлении для сигнала, показанного на рис.1, приведен на рис2. При рассмотрении спектра фаз следует учитывать периодичность 2p угловой частоты (при уменьшении фазового значения до величины менее -p происходит сброс значения -2p). 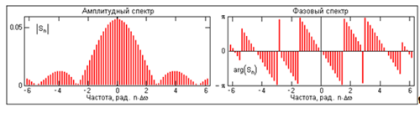 Рис. 3 - Модуль и аргумент спектра 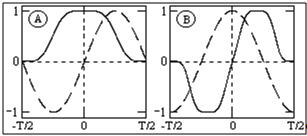 Рис. 4 - Ортогональность функций Если функция s(t) является четной, то все значения B(nDw) по (5) равны нулю, т.к. четные функции ортогональны синусным гармоникам и подынтегральное произведение s(t)·sin(nDwt) дает нулевой интеграл. Следовательно, спектр функции будет представлен только вещественными коэффициентами. Напротив, при нечетности функции s(t) обнуляются все значения коэффициентов А(nDw) (нечетные функции ортогональным косинусным гармоникам) и спектр является чисто мнимым. Этот фактор не зависит от выбора границ задания периода функции на числовой оси. На рис.3(А) можно наглядно видеть ортогональность первой гармоники синуса и четной функции, а на рис.3(В) соответственно косинуса и нечетной функции в пределах одного периода. Учитывая кратность частот последующих гармоник первой гармонике спектра, ортогональность сохраняется для всех гармоник ряда Фурье. При n = 0 имеем Во = 0, и получаем постоянную составляющую сигнала: S0≡ Ao≡ Ro ≡ (1/T) Тригонометрическая форма рядов Фурье Объединяя в (1) комплексно сопряженные составляющие (члены ряда, симметричные относительно центрального члена ряда S0), можно перейти к ряду Фурье в тригонометрической форме: s(t) = Ао+2 Значения An, Bn вычисляются по формулам (4-5), значения Rn и jn - по (3'). Ряд (6) представляют собой разложение периодического сигнала s(t) на сумму вещественных элементарных гармонических функций (косинусных и синусных) с весовыми коэффициентами, удвоенные значения которых (т.е. значения 2An, 2Bn) не что иное, как реальные амплитуды соответствующих гармонических колебаний с частотами nDw. Совокупность амплитудных значений этих гармоник образует односторонний физически реальный (только для положительных частот nDw) спектр сигнала. Для сигнала на рис.1, например, он полностью повторяет правую половину приведенных на рисунке спектров с удвоенными значениями амплитуд (за исключением значения Ао на нулевой частоте, которое, как это следует из (6), не удваивается). Но такое графическое отображение спектров используется довольно редко. В технических приложениях более широкое применение для отображения физически реальных спектров находит формула (6'). Спектр амплитуд косинусных гармоник 2Rn при таком отображении называется амплитудно-частотным составом сигнала, а спектр фазовых углов гармоник – фазовой характеристикой сигнала. Форма спектров повторяет правую половину соответствующих двусторонних спектров (см. рис.2) также с удвоенными значениями амплитуд. Для четных сигналов отсчеты фазового спектра могут принимать только значения 0 или p, для нечетных соответственно p/2. 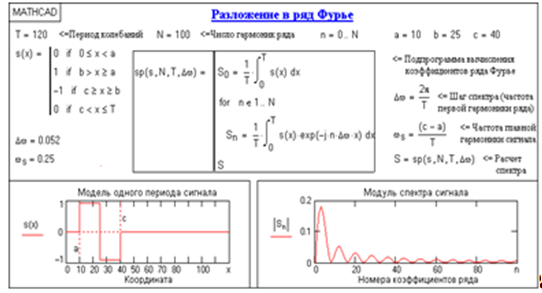 Рис. 5 - Расположение в ряд Фурье На рис.4 показано разложение в комплексный ряд Фурье модельного сигнала, выполненное в среде Mathcad. Модель сигнала задана с тремя разрывами первого рода (скачками). Любой скачок функции содержит все частоты диапазона до бесконечности, в связи с чем ряд Фурье также бесконечен и очень медленно затухает. На рисунке приведены значения только первых 100 членов ряда, при этом график спектра сигнала, как это обычно принято на практике, построен в виде огибающей значений модулей коэффициентов ряда Sn и только по области положительных значений n. Программа на рис.5 продолжает программу рис.4 и показывает реконструкцию сигнала по его спектру при ограничении числа членов ряда Фурье. На верхнем графике рисунка приведен реконструированный сигнал при N = 8 (гармоники первого пика спектра, центр которого соответствует главной гармонике сигнала и члену ряда n = ws/Dw), N = 16 (гармоники двух первых пиков) и N=40 (пять первых пиков спектра). Естественно, что чем больше членов ряда включено в реконструкцию, тем ближе реконструированный сигнал к форме исходного сигнала. 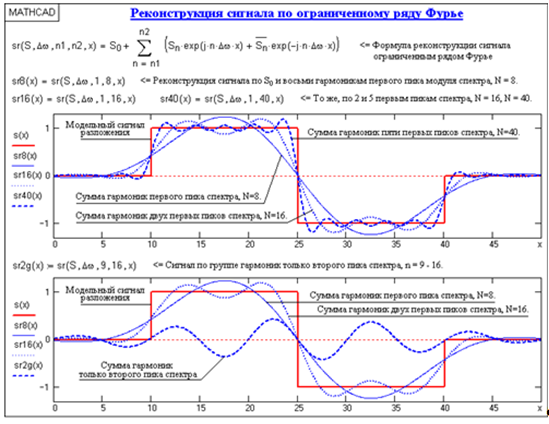 Рис. 6 - Реконструкция сигнала по ограниченному ряду Фурье сигнал синусоида фурье спектр На рис.6. приведен пример разложения в ряд Фурье одного периода T=(a,c) модельного периодического сигнала sq(x), представленного информационным сигналом s(x) в сумме с шумовым сигналом. Спектр шумов близок к спектру белого шума (равномерное распределение энергии шумов по всем частотам спектра). На спектре модельного сигнала достаточно четко выделяется диапазон частот информационного сигнала. Реконструкция сигнала с ограничением ряда Фурье гармониками только информационного сигнала (сигнал sr5(x), N=5) дает сглаженную форму сигнала по минимуму среднеквадратического расхождения с модельным сигналом для данного количества членов ряда, но только по периоду разложения (а, с), и наиболее точное приближение к информационному сигналу. При увеличении в реконструкции количества членов ряда Фурье восстановленный сигнал начинает приближаться к модельному сигналу, но только по данному периоду T=(a,c), при этом расхождение с информационным сигналом увеличивается. Заметим, что спектр сигнала может определяться и по нескольким периодам сигнала, что повышает точность реконструкции информационного сигнала. В ряд Фурье может разлагаться и произвольная непериодическая функция, заданная (ограниченная, вырезанная из другого сигнала, и т.п.) на интервале (a,b), если нас не интересует ее поведение за пределами данного интервала. Однако следует помнить, что применение формул (1-6) автоматически означает периодическое продолжение данной функции за пределами заданного интервала (в обе стороны от него) с периодом Т = b-a. При этом на краях интервала может возникнуть явление Гиббса, если уровень сигнала на краях не совпадает и образуются скачки сигнала при его периодическом повторении, как это видно на рис.7. При разложении исходной функции в ограниченный ряд Фурье и его обработке в частотной области на самом деле при этом обрабатывается не исходная функция, а реконструированная из ограниченного ряда Фурье. 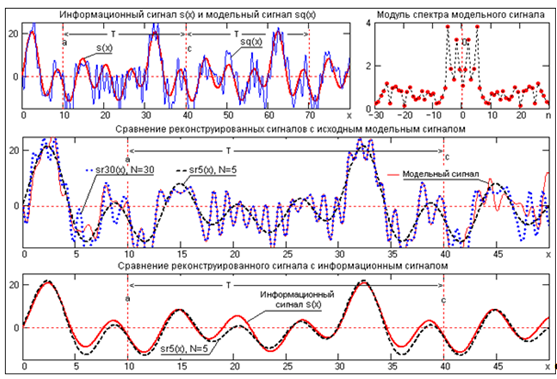 Рис. 7 При усечении рядов Фурье определенное искажение функций существует всегда. Но при малой доле энергии отсекаемой части сигнала (при быстром затухании спектров функций) этот эффект может быть и мало заметен. На скачках и разрывах функций он проявляется наиболее ярко. 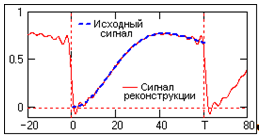 Рис. 8 Преобразование Лапласа Если условие (9) не выполняется, то определенные приближения спектральных плотностей вычисляются с использованием специальных методов, одним из которых является одностороннее преобразование Лапласа. 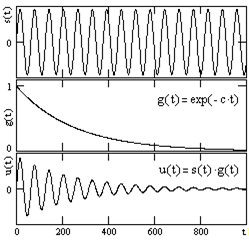 Рис. 9 Допустим, что функция s(t) задана на интервале (0, ), равна нулю при t<0, а интеграл спектральной функции (2) расходится. Умножим s(t) на экспоненциальную функцию exp(-st), где s - положительная константа, и выберем значение s таким, чтобы произведение u(t) = s(t)exp(-st) удовлетворяло условию абсолютной интегрируемости. Сущность данной операции хорошо видна на рис.6 (s=с). Интегрируемость функции u(t) может быть установлена для любой функции s(t) соответствующим выбором коэффициента s. При этом спектральная плотность функции u(t) может быть вычислена по формуле (2): U(w,s) = После объединения экспоненциальных функций это выражение можно переписать следующим образом: U(s+jw) = Соответствующее обратное преобразование Фурье функции U(s+jw): (1/2p) Для восстановления функции s(t) достаточно умножить обе части данного выражения на exp(st), объединить экспоненциальные множители под интегралом и заменить переменную интегрирования w на s+jw: s(t) = (1/2pj) Обозначим комплексную переменную s+jw в выражениях (10,11) через р(оператор Лапласа) и получим общепринятую форму прямого и обратного преобразования Лапласа: S(p) = s(t) = (1/2pj) 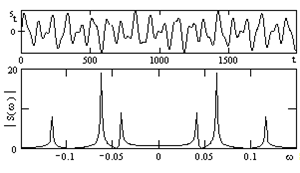 Рис. 10 Сигнальную функцию s(t) в преобразованиях Лапласа обычно называют оригиналом, а ее спектральную функцию S(p) - изображением оригинала. Пример спектральной функции Лапласа для оригинала - сложного и неограниченного во времени сигнала, состоящего из каузальной суммы трех гармоник, приведен на рис. 4.2.7. По спектральной функции Лапласа можно выделить эти три основных частоты сигнала и оценить соотношение их амплитуд. Ширина пиков спектральной функции при выделении "чистых" гармоник зависит от значения коэффициента s и уменьшается при его уменьшении. Преобразование Лапласа справедливо только в области сходимости интеграла (4.2.10), которая определяется абсциссой абсолютной сходимости s0 (при s ≥ s0): Если вместо р в изображениях оригинала подставить переменную jw, то будут получены спектральные функции, полностью идентичные преобразованию Фурье каузальных функций (имеющих нулевые значения при t<0). |
