теплофизика. 1. Элементарные и сложные виды теплообмена
 Скачать 3.23 Mb. Скачать 3.23 Mb.
|
Коэффициент теплоотдачи и его связь с коэффициентом теплопередачиКоэффициентом теплопередачи через плоскую стенку связан с коэффициентами теплоотдачи выражением:  26. Роль теории пограничного слоя. Пограничный слой, тонкая область течения вязкой жидкости (газа), которая образуется у поверхности обтекаемого ею твердого тела или на границе раздела двух потоков жидкости с различными скоростями, температурами или химическим составом. Возможность практического использования модели вязкой жидкости открылась благодаря тому, что действие вязкости проявлялось в узкой области вблизи граничной поверхности. В самом деле, из-за прилипания жидкости на поверхности тела обтекания скорость равна нулю. Следовательно, вблизи поверхности число Рейнольдса . Это означает, что непосредственно у обтекаемой поверхности, где , вязкость играет наиболее существенную роль по сравнению с областью течения, удаленной от тела. Толщина динамического П.С. определяется критерием Рейнольдса (см. Рейнольдса числоRe), который характеризует соотношение между инерционными силами и силами внутреннего трения. +Чем больше Re, тем меньше толщина П.С. по сравнению с характерным размером тела. Помимо динамического П.С. при обтекании тела можно выделить также тепловой (температурный) П.С., образующийся в случае несовпадения температуры поверхности тела и температуры жидкости. В тепловом П.С. температуры жидкости непосредственно у стенки равна температуры поверхности тела. Если тело обтекается жидкостью с малой скоростью, то внутри теплового П.С. происходит монотонное изменение температуры жидкости от температуры поверхности до температуры внешнего потока. Если же тело обтекается сверхзвуковым потоком газа, то внутри теплового П.С. вследствие торможения газа и перехода кинетической энергии во внутреннюю энергию молекул может возникать максимум температуры. +концентрационный (диффузионный) П.С., образующийся при протекании на стенке химической реакции или же при вдуве инородного газа через проницаемую поверхность тела. 27. Использование теории подобия при исследовании процессов теплоотдачи. При изучении теплоотдачи число Нуссельта в уравнении подобия всегда является определяемым (искомым), так как в него входит общая характеристика интенсивности теплоотдачи – коэффициент теплоотдачи α. Числа подобия, входящие в правую часть уравнения подобия, учитывают влияние различных факторов на коэффициент теплоотдачи и являются определяющими. Nu = f (Re, Gr, Pr). (3.21) Число Рейнольдса отражает влияние вынужденного движения теплоносителя, число Грасгофа влияние свободного движения и критерий Прандтля – влияние физических свойств теплоносителя (жид-кости или газа) на коэффициент теплоотдачи. Свободное движение всегда сопутствует явлению теплоотдачи, но при вынужденном движении теплоносителя и развитом турбулентном режиме оно имеет второстепенное значение и не отражается на величине коэффициента теплоотдачи. Поэтому для таких задач уравнение подобия не включает число Грасгофа: Nu = f (Re, Pr). (3.22) При свободном движении теплоносителя, когда вынужденная конвекция отсутствует, в уравнение подобия не входит число Рейнольдса: Nu = f (Gr, Pr). (3.23) Число Прандтля для газов изменяется не существенно в значительном диапазоне изменения температуры. Поэтому уравнение подобия для конкретных газов может не включать числа Pr, его среднее значение войдет в постоянную уравнения. Например, для воздуха при турбулентном режиме движения можно записать: Nu = f (Re). (3.24) Для удобства обработки опытных данных уравнение подобия принято представлять в виде степенной функции: Nu = с Rek Grm Prn, (3.25) где с, к, m, n – опытные коэффициенты. 28. Определяющий размер и определяющая температура. Характерный линейный размер системы ℓ, входящий в числа подобия, называется определяющим. Теория подобия не дает одно-значного ответа на вопрос, какой размер должен быть принят за оп-ределяющий. Если в условия однозначности входит несколько раз-меров, то за определяющий принимается тот, который в наибольшей мере влияет на процесс конвективного теплообмена. Для труб круглого сечения таким определяющим линейным размером является внутренний диаметр трубы. Для каналов некруглого сечения вместо диаметра берется так называемый эквивалентный диаметр dэкв = 4F/P, (3.26) где F – площадь поперечного сечения канала; P – полный (смоченный) периметр сечения независимо от того, какая часть этого периметра участвует в теплообмене. определяющей температуры – температуры, при которой выбираются физические параметры теплоносителя, входящие в числа подобия. В качестве определяющей можно выбрать среднюю температуру теплоносителя Тж, среднюю температуру стенки Тст или среднюю температуру пограничного слоя Тm Тm = (Тст + Тж)/2. (3.27) Наиболее часто в качестве определяющей принимается средняя температура теплоносителя. 29. Связь между теплоотдачей и трением. Рассмотрим безнапорное течение жидкости с физическими свойствами, не зависящими от температуры, при отсутствии массовых сил. Коэффициенты вязкости и температуропроводности в уравнениях движения и энергии могут быть равны следующим значениям: 1) при ламирарном режиме течения в пограничном слое 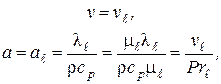 где  - число Прандтля при ламинарном режиме течения; - число Прандтля при ламинарном режиме течения;2) при турбулентном режиме течения в пограничном слое 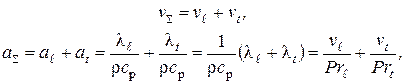 где 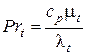 - число Прандтля при турбулентном режиме течения. - число Прандтля при турбулентном режиме течения.При ламинарном пограничном слое на пластине и числе коэффициенты вязкости и температуропроводности будут равны: Воспользуемся подобием скоростных и температурных полей для получения количественной связи между интенсивностью теплоотдачи и трением. Для этого определим плотность теплового потока и напряжение трения на поверхности стенки: 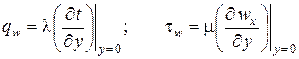 . .Продифференцировав по координате y и разделив первое уравнение на второе получим: 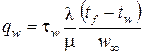 . (2.20) . (2.20)Полученное равенство отражает связь между теплоотдачей и трением и называется аналогией Рейнольдса. 30. Дифференциальные уравнения ламинарного и турбулентного пограничного слоя систему дифференциальных уравнений ламинарного пограничного слоя (уравнения Прандтля): 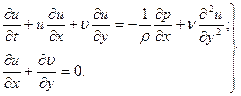 (2.123) (2.123)Для получения единственного решения системы (2.123) необходимо сформулировать начальные и граничные условия. Начальное условие записывается в виде: при t = 0: u = u (0, x, y). (2.125) На твердой стенке (внутренней границе) должно выполняться граничное условие прилипания: при y = 0: u = 0, . (2.126) На границе слева: при : . (2.127) На внешней границе можно ставить граничное условие либо при , и тогда говорят об асимптотическом пограничном слое, либо при , тогда говорят о слое конечной толщины. Выбрав граничное условие для асимптотического пограничного слоя: при : Можно получить вместо системы (2.123) одно уравнение с граничными условиями: при при при В случае турбулентного течения соответствующие уравнения пограничного слоя получаются из уравнений Рейнольдса Сохраняя те же допущения относительно осредненного движения, что и в предыдущем разделе, а также производя дополнительную оценку рейнольдсовых напряжений, можно получить следующую систему дифференциальных уравнений турбулентного пограничного слоя: 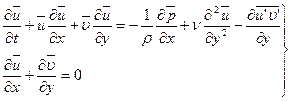 (2.131) (2.131)Опуская знак осреднения и используя гипотезу Буссинеска, этой системе формально можно придать вид:  (2.132) (2.132)где - эффективная вязкость, включающая в себя молекулярную вязкость (ламинарная составляющая) и вихревую вязкость (турбулентная составляющая). 31. Теплоотдача при свободном движении теплоносителя в неограниченном и ограниченном пространстве в гравитационном поле массовых сил. В гравитационном поле массовых сил свободное движение возникает в результате различной плотности холодных и горячих объемов теплоносителя. Нагреваемые от стенки объемы теплоносителя всплывают, а охлаждаемые опускаются. Характер движения теплоносителя вблизи стенки зависит от формы поверхности, ее расположения в пространстве и направления теплового потока. Задачи конвективного теплообмена при свободном движении жидкости в неограниченном пространстве были решены экспериментально. Теплоотдача определялась для тел различной формы и размеров. Результаты экспериментальных исследований были представлены зависимостью Здесь – критерий Рэлея; 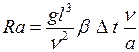 . .существует три режима переноса теплоты в зависимости от произведения (Рис. 5.4 и таблица 5.1). При первом режиме (кривая 1 на рисунке 5.4) теплоотдача слабо зависит от произведения и теплота передается в основном теплопроводностью.  При втором режиме (кривая 2 на рис. 5.4) существует ламинарный пограничный слой, теплота переносится вследствие свободной конвекции при ламинарном режиме. При третьем режиме (кривая 3 на рис. 5.4) теплота передается вследствие свободной конвекции при турбулентном режиме движения жидкости.  32. Влияние формы поперечного сечения обтекаемых тел на теплоотдачу. Цилиндрическая поверхность при поперечном обтекании является хорошим турбулизатором потока. Ламинарное, плавное и безотрывное обтекание наблюдается здесь очень редко, только когда Re < 5. В большинстве практических случаев при обтекании цилиндра в задней (по ходу потока) его части происходит срыв пограничного слоя и турбулизация теплоносителя. При постоянстве массового расхода в минимальном сечении потока (рис. 2.48, а) средняя скорость течения наибольшая и направлена так, что силы инерции увлекают частицы жидкости в направлении X, что и является причиной их отрыва от слоя и турбулизации. С увеличением числа Re интенсивность вихреобразования растет, уменьшается угол отрыва слоя q> и при Re > 1000 за трубой возникает несглаживающаяся турбулентная дорожка. Картина нарастания пограничного слоя для этого случая показана на рис. 2.48, б. Толщина слоя увеличивается симметрично от носовой части трубы к корме, в кормовой части при углах ср = 95... 115° происходит срыв, а после срыва слой вновь начинает нарастать. Подобным же образом ведет себя и тепловой пограничный слой, что хорошо объясняет наличие трех максимумов на эпюре локальных значений а, приведенной на рис. 2.48, в. При Re < 105 абсолютный максимум имеет место на носовой зоне, при Re > 105 — в кормовой части трубы. Для расчетов среднего для всей поверхности значения коэффициента теплоотдачи а на основании экспериментов получены следующие критериальные уравнения: 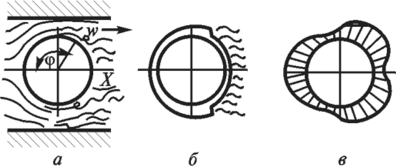 Рис. 2.48. Обтекание цилиндра при Re < 1000  при Re > 1000 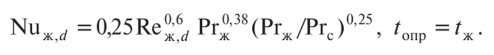 Любой пучок является сильнейшим турбулизатором потока. При этом трубы первого ряда (по ходу теплоносителя) работают точно так же, как одиночная труба. А вот на трубы второго, третьего и других рядов набегает поток, уже турбулизированный трубами предыдущих рядов. Поэтому интенсивность теплоотдачи здесь несколько увеличивается.  Рис. 2.49. Схемы трубных пучков: а — коридорный; 6 — шахматный; в — каскадный с расположением труб по сторонам и вершинам шестиугольников; г — каскадный с наклонным расположением
| ||||||||||||
