Физика 9 класс. 1. Физика. Методы познания природы. Физические явления
 Скачать 5.42 Mb. Скачать 5.42 Mb.
|
28. Механические свойства твердых тел. Закон Гука. Модель Юнга.Механические свойства твёрдых тел. Упругость, пластичность, хрупкость. При применении твердых материалов, а также при их переработке необходимо учитывать их механические свойства. При этом различают твердые и мягкие тела, вязкие и хрупкие, упругие и пластичные. Причиной этих свойств во многом являются силы связи между молекулами материала. Если материал может сопротивляться проникновению в него других тел, то он тверже, чем другие. Под твердостью понимают сопротивление материала, которое он создает при вдавливании или царапании его поверхности другим телом. Оценка твердости материала проводится с помощью простого испытания на твердость методом царапания. Более мягкий материал будет царапаться более твердым. При этом различают степени твердости 1—10. Для оценки различным минералам приписываются различные степени твердости. Твердыми материалами, например, являются алмаз, твердые строительные материалы, например гранит, клинкерные стеновые камни О мягкости материала говорят, когда его можно сжать с приложением небольшой силы или процарапать другим материалом. Мягкими материалами являются, например, свинец, гипс и вспененные синтетические материалы Под вязкостью понимают способность материала под воздействием изгибных, ударных и толчковых нагрузок хотя и поддаваться, но при этом не разрушаться. Вязкими являются такие материалы, как сталь, свинец, дерево, кожа и термопластичные пластмассы. Они в основном имеют волокнистое строение. Под хрупкостью понимают свойство материала под воздействием изгибающих, ударных и толчковых нагрузок не изменять свою форму, а сразу разрушаться. К хрупким материалам относится, например, стекло, природные камни, искусственные стеновые камни и бетон. Строение их в основном зернистое. Хрупкость материалов считается недостатком. Упругость — это свойство материала позволять себя сжимать или растягивать, а после снятия нагрузки — возвращаться к первоначальной форме. Упругими материалами являются, например, резина и рессорная сталь. Пластичностью называют свойство материалов под воздействием нагрузки изменять свою форму и сохранять эту новую форму после снятия нагрузки. Рис.1 Диаграмма растяжения. Диаграммой растяжения принято называть графическую зависимость σ от ε. По экспериментальным значениям относительного удлинения ε можно вычислить соответствующие им значения нормального напряжения σ, возникающего в упруго деформированном теле. Пример диаграммы растяжения для металлического образца изображен на рис.1. На участке 0–1 график имеет вид прямой, проходящей через начало координат. Это значит, что до определенного значения напряжения деформация является упругой и выполняется закон Гука, согласно которому нормальное напряжение пропорционально относительному удлинению. Максимальное значение нормального напряжения σП, при котором еще выполняется закон Гука, называют пределом пропорциональности. При дальнейшем увеличении нагрузки зависимость напряжения от относительного удлинения становится нелинейной (участок 1–2), хотя упругие свойства тела еще сохраняются. Максимальное значение σy нормального напряжения, при котором еще не возникает остаточная деформация, называют пределом упругости. (Предел упругости лишь на сотые доли процента превышает предел пропорциональности). Увеличение нагрузки выше предела упругости (участок 2–3) приводит к тому, что деформация становится остаточной. Затем образец начинает удлиняться практически при постоянном напряжении (участок 3–4 графика). Это явление называют текучестью материала. Нормальное напряжение σТ, при котором остаточная деформация достигает заданного значения, называют пределом текучести. При напряжениях, превышающих предел текучести, упругие свойства тела в известной мере восстанавливаются, и оно вновь начинает сопротивляться деформации (участок 4–5 графика). Максимальное значение нормального напряжения σпр, при превышении которого происходит разрыв образца, называют пределом прочности. Зададимся вопросом, какой физический смысл имеет модуль Юнга? Запишем закон Гука в виде: . Если удлинение ΔL будет равно первоначальной длине образца L, то . Это означает, что модуль Юнга равен тому напряжению, которое вызывает удлинение образца вдвое. Конечно, материалов, которые можно удлинить в два раза, кроме разве резины и некоторых полимеров, нет. Однако как характеристика упругих свойств материала модуль Юнга служит отлично. Для стали модуль Юнга примерно равен 2,1·1011 Н/м2. Почему примерно? Да потому, что марок сталей очень много. Соответственно и модуль Юнга пружинной стали больше модуля Юнга стали, из которой делаются гвозди. Свинец – мягкий металл, но и он обладает упругостью, а его модуль Юнга в 15 раз меньше, чем модуль Юнга стали. Все остальные металлы имеют модуль Юнга больше, чем у свинца, но меньше, чем у стали. Другой важной характеристикой конструкционного материала является предел прочности. Предел прочности у разных материалов также сильно отличается. У стали предел прочности наибольший. Поэтому сталь – основной конструкционный материал. При проектировании любых конструкций учитывается предел прочности, и возможные напряжения должны быть в несколько раз (обычно в 10 раз) меньше предела прочности. Существует специальный раздел в прикладной науке – сопротивление материалов. Его изучают во всех технических вузах, готовящих специалистов по конструированию и эксплуатации машин и механизмов. Интересно отметить, что стальная проволока, повешенная за один конец, растягивается под действием собственного веса. А если такая проволока будет иметь длину L = 4,2 км, то она оборвется под действием собственного веса. Проволока из свинца оборвется под действием собственного веса при длине всего в 120 метров. Все машины и механические конструкции – башни, мосты, арочные конструкции – рассчитываются так, чтобы напряжения ни в одном месте конструкции не превышали предела упругости. В настоящее время существуют стальные мосты, длина пролета которых (расстояние между опорами) превышает 1 000 метров. Зако́н Гу́ка — утверждение, согласно которому деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. п.), пропорциональна приложенной к этому телу силе. Открыт в 1660 году английским учёным Робертом Гуком[1]. Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях. Закон Гука для тонкого стержня[править | править вики-текст] Для тонкого растяжимого стержня закон Гука имеет вид: Здесь F — сила, которой растягивают (сжимают) стержень, \Delta l — абсолютное удлинение (сжатие) стержня, а k — коэффициент упругости (или жёсткости). Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения S и длины L) явно, записав коэффициент упругости как Величина E называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала. Если ввести относительное удлинение и нормальное напряжение в поперечном сечении то закон Гука для относительных величин запишется как В такой форме он справедлив для любых малых объёмов материала. Также при расчёте прямых стержней применяют запись закона Гука в относительной форме Обобщённый закон Гука[править | править вики-текст] В общем случае напряжения и деформации описываются тензорами второго ранга в трёхмерном пространстве (имеют по 9 компонент). Связывающий их тензор упругих постоянных является тензором четвёртого ранга и содержит 81 коэффициент. Вследствие симметрии тензора , а также тензоров напряжений и деформаций, независимыми являются только 21 постоянная. Закон Гука выглядит следующим образом: где — тензор напряжений, , — тензор деформаций. Для изотропного материала тензор содержит только два независимых коэффициента. Благодаря симметрии тензоров напряжения и деформации, закон Гука может быть представлен в матричной форме. Для линейно упругого изотропного тела: где E — модуль Юнга, \ — коэффициент Пуассона, Модуль Юнга (модуль продольной упругости) — физическая величина, характеризующая свойства материала сопротивляться растяжению/сжатию при упругой деформации[1]. Назван в честь английского физика XIX века Томаса Юнга. В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал среды и процесса. В Международной системе единиц (СИ) измеряется в ньютонах на метр в квадрате или в паскалях. Является одним из модулей упругости. Модуль Юнга рассчитывается следующим образом: F — нормальная составляющая силы, S — площадь поверхности, по которой распределено действие силы, l — длина деформируемого стержня, — модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина l). Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне: 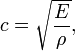 где — плотность вещества. где — плотность вещества. |
