Физика 9 класс. 1. Физика. Методы познания природы. Физические явления

• Название: 1. Физика. Методы познания природы. Физические явления
• Анкор: Физика 9 класс
• Дата: 13.05.2022
• Размер: 5.42 Mb.
• Имя файла: fizika_90_voprosov.docx
• Тип: Документы; #527598
• страница: 1 из 64

1.Физика. Методы познания природы. Физические явления.

Физика – одна из наук, изучающих природу. Свое название физика получила от греческого слова «фюзис», что в переводе означает «природа». Поначалу физикой называли науку, которая рассматривала любые природные явления. Впоследствии же круг изучаемых физикой явлений был достаточно четко обозначен.

Что же называют явлениями природы? Явления природы – это изменения, которые постоянно в ней происходят.

Среди физических явлений прежде всего необходимо назвать:

· механические, которые связаны с движением тел. Физика не только рассматривает и описывает движение, но и объясняет причины, по которым тело начинает или прекращает движение, движется или покоится;

· тепловые, обусловленные внутренним строением вещества (изучает термодинамика);

· электромагнитные;

· световые.

Измерить физическую величину – значит сравнить ее с однородной величиной, принятой за единицу величины. При проведении измерений используют разнообразные измерительные приборы и инструменты – линейки, термометры, секундомеры, амперметры и др. Для каждой физической величины существуют свои единицы измерения. Например, длину измеряют в метрах, площадь – в квадратных метрах, температуру – в градусах Цельсия. Для удобства в разных странах стараются пользоваться одинаковыми единицами. Наибольшее распространение получила Международная система единиц (СИ).

При изучении физических явлений устанавливают связи между величинами. Если связь между величинами носит устойчивый характер, ее называют физическим законом, который является математическим выражением закона природы.

Объяснить, почему то или иное явление протекает так, а не иначе, выяснить причину явления позволяет физическая теория. Курс физики дает возможность не только объяснить, но и предсказать ход явлений, свойства тел.

Каждая физическая теория описывает определенные явления окружающего материального мира. Все они связаны между собой, поскольку материальный мир един. Совокупность всех наших знаний о мире представляет собой физическую картину мира.

2. Механическое движение. Системы отсчета. Относительность механического движения. Характеристики механического движения.

Механическим движением называют изменение положения тела (или его частей) относительно других тел. Например, человек едущий на эскалаторе в метро, находится в покое относительно самого эскалатора и перемещается относительно стен туннеля; Гора Эльбрус находится в покое относительно Земли и движется вместе с Землёй относительно Солнца. Из этих примеров видно, что всегда надо указать тело, относительно которого рассматривается движение, его называют телом отсчёта. Система координат, тело отсчёта с которым она связана, и выбранный способ измерения времени образуют систему отсчёта.

Механическое движение характеризуется тремя физическими величинами: перемещением, скоростью и ускорением. Направленный отрезок прямой, проведённый из начального положения движущейся точки в её конечное положение, называется перемещением (S). Это величина векторная. Единица перемещения – метр.

3. Виды механического движения. Графики скорости и пути.

Механическое движение – это изменение положения тела в пространстве относительно других тел.

Например, автомобиль движется по дороге. В автомобиле находятся люди. Люди движутся вместе с автомобилем по дороге. То есть люди перемещаются в пространстве относительно дороги. Но относительно самого автомобиля люди не движутся. В этом проявляется относительность механического движения. Далее кратко рассмотрим основные виды механического движения.

Поступательное движение – это движение тела, при котором все его точки движутся одинаково.

Например, всё тот же автомобиль совершает по дороге поступательное движение. Точнее, поступательное движение совершает только кузов автомобиля, в то время как его колёса совершают вращательное движение.

Вращательное движение – это движение тела вокруг некоторой оси. При таком движении все точки тела совершают движение по окружностям, центром которых является эта ось.

Упоминавшиеся нами колёса совершают вращательное движение вокруг своих осей, и в то же время колёса совершают поступательное движение вместе с кузовом автомобиля. То есть относительно оси колесо совершает вращательное движение, а относительно дороги – поступательное.

Колебательное движение – это периодическое движение, которое совершается поочерёдно в двух противоположных направлениях.

Например, колебательное движение совершает маятник в часах.

Поступательное и вращательное движения – самые простые виды механического движения.

Если траектория движения точки известна, то зависимость длины пути s, пройденного точкой, от истекшего промежутка времени t дает полное описание этого движения. Мы видели, что для равномерного движения такую зависимость можно дать в виде формулы (9.3). Связь между s и t для отдельных моментов времени можно задавать также в виде таблицы, содержащей соответственные значения промежутка времени и длины пройденного пути. Пусть нам дано, что скорость некоторого равномерного движения равна 2 м/сек. Формула (9.3) имеет в этом случае вид s=2t. Составим таблицу пути и времени такого движения:

t, сек   1       2       3       4       5       6    ...
S,  м    2      4       6       8      10      12    ...

Рис. 1. График пути равномерного движения со скоростью 2 м/сек.

Зависимость одной величины от другой часто бывает удобно изображать не формулами или таблицами, а графиками, которые более наглядно показывают картину изменения переменных величин и могут облегчать расчеты. Построим график зависимости пройденного пути от времени для рассматриваемого движения. Для этого возьмем две взаимно перпендикулярные прямые — оси координат; одну из них (ось абсцисс) назовем осью времени, а другую (ось ординат) — осью пути. Выберем масштабы для изображения промежутков времени и длин пути и примем точку пере-сечения осей за начальный момент и за начальную точку на траектории. Нанесем на осях значения времени и пройденного пути для рассматриваемого движения (рис. 1). Для «привязки» длин пройденного пути к моментам времени проведем из соответственных точек на осях (например, точек 3 сек и 6 м) перпендикуляры к осям. Точка пересечения перпендикуляров соответствует одновременно обеим величинам: длине пути s и моменту времени t,— этим способом и достигается «привязка». Такое же построение можно выполнить и для любых других моментов времени и соответственных длин путей, получая для каждой такой пары значений «время—путь» одну точку на графике. На рис. 18 выполнено такое построение, заменяющее обе строки таблицы одним рядом точек. Если бы такое построение было выполнено для всех моментов времени, то вместо отдельных точек получилась бы сплошная линия (также показанная на рисунке). Эта линия и называется графиком зависимости пути от времени или, короче, графиком пути.

Рис. 19. К упражнению 12.1.

В нашем случае график пути оказался прямой линией. Можно показать, что график пути равномерного движения всегда есть прямая линия; и обратно: если график зависимости пути от времени есть прямая линия, то движение равномерно.

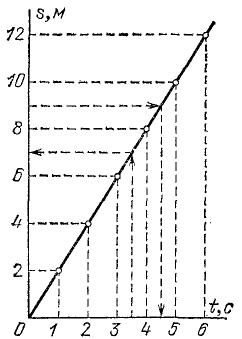
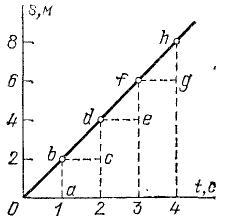
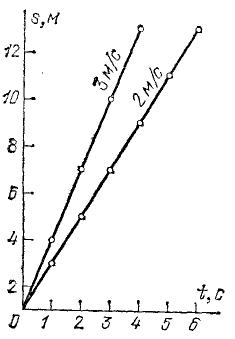
Упражнение. 12.1. Доказать это положение, пользуясь рис. 19.

Повторяя построение для другой скорости движения, найдем, что точки графика для большей скорости лежат выше, чем соответственные точки графика для меньшей скорости (рис. 20). Таким образом, чем больше скорость равномерного движения, тем круче прямолинейный график пути, т. е. тем больший угол он составляет с осью времени.

Наклон графика зависит, конечно, не только от величины скорости, но и от выбора масштабов времени и длины. Например, график, изображенный на рис. 21, дает зависимость пути от времени для того же движения, что и график рис. 18, хотя и имеет другой наклон. Отсюда ясно, что сравнивать движения по наклону графиков можно только в том случае, если они вычерчены в одном и том же масштабе.

С помощью графиков пути можно  легко решать разные задачи о движении. Для примера на рис. 18 показаны пунктиром построения, которые нужно выполнить, чтобы решить следующие задачи для данного движения: 1) Какой путь пройден за 3,5 сек? 2) За сколько времени пройден путь 9 м? На рисунке графическим путем (пунктир) найдены ответы:  1) 7 м; 2) 4,5 сек.

Рис. 20. Графики   пути   равно-мерных движений со скоростями 2 м/сек и 3 м/сек.

Рис. 21. График того же движения, что на рис. 18, вычерченный в другом масштабе.

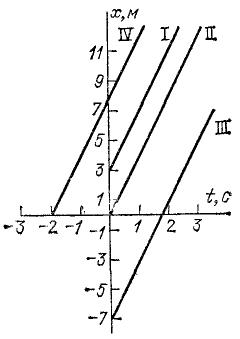
Упражнение. 12.2. По графику рис. 18 найти, на каком расстоянии от начальной точки окажется движущаяся точка через 2 сек после того, как она пройдет путь, равный 6 м.

В нашем примере график проходит через точку пересечения осей. Это значит, что в начальный момент (t=0) движущаяся точка находится в начальной точке траектории s=0. Если же в начальный момент движущаяся точка находилась не в начальной, а в какой-то другой точке, то при построении графика придется откладывать пройденные пути за тот или иной промежуток времени после t=0 от этой другой точки.

Например, на рис. 22 прямая I есть график движения, происходящего со скоростью 4 м/сек, причем движущаяся точка в начальный момент находилась в точке s0=3 м. Для сравнения на этом же рисунке дан график движения, которое происходит с той же скоростью, но при котором в начальный момент движущаяся точка находится в начальной точке траектории (прямая II).

На предыдущих графиках были изображены движения, происходящие только в положительной стороне от начальной точки. Будем, согласно § 6, считать длины путей по другую сторону от начальной точки отрицательными. На графике их можно изображать на оси пути вниз от оси времени.
Например, на рис. 22 прямая III есть график движения, происходящего с той же скоростью 4 м/сек, причем в начальный момент движущаяся точка находится на расстоянии 7 м от начальной в отрицательную сторону по траектории (s0=-7).

Мы видим, что наклоны всех трех графиков одинаковы: наклон зависит только от скорости движущейся точки, а не от ее начального положения. При изменении начального положения весь график просто переносится параллельно самому себе вдоль оси пути вверх или вниз на соответственное расстояние.

Вспомним, что выбор начального момента времени при описании данного движения также произволен. Можно начать рассматривать движение и после, и до момента времени, принятого за начальный. Моментам, предшествующим начальному моменту времени t=0, приписывают отрицательные значения. Так, моменты —1 сек, —2 сек и т. д. обозначают моменты за 1 сек, за 2 сек и т. д. от начального. Отрицательные моменты времени откладывают на оси времени влево от начала координат.

Рис. 22. Графики движений с одной и той же скоростью, но при различных начальных положениях движущегося тела.

Итак, можно строить графики пути для любых моментов времени, как до, так и после начального момента, и для любых положений точки, как по одну, так и по другую сторону от начальной точки. Прямая IV на рис. 22 есть график такого движения, происходящего со скоростью 4 м/сек, при котором точка была в начальном положении за 2 сек до начального момента.

Наконец, на графиках можно изображать движения, происходящие с отрицательными скоростями: это будут прямые, наклоненные вниз (рис. 23). Для таких движений длина пути уменьшается с течением