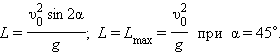На рис.1 представлены графики скоростей для трех случаев движения тела с ускорением a = –g. График I соответствует случаю свободного падения тела без начальной скорости с некоторой высоты h. Падение происходило в течение времени tп = 1 с. Из формул для свободного падения легко получить: h = 5 м (все числа в этих примерах округлены, ускорение свободного падения принято равным 10 м/с2). График II – случай движения тела, брошенного вертикально вверх с начальной скоростью υ0 = 10 м/с. Максимальная высота подъема h = 5 м. Тело возвращается на землю через время t = 2 с. График III – продолжение графика I. Свободно падающее тело при ударе о землю отскакивает (мячик), и его скорость за очень короткое время меняет знак на противоположный. Дальнейшее движение тела не отличается от случая II. Задача о свободном падении тел тесно связана с задачей о движении тела, брошенного под некоторым углом к горизонту. Для кинематического описания движения тела удобно одну из осей системы координат (ось OY) направить вертикально вверх, а другую (ось OX) – расположить горизонтально. Тогда движение тела по криволинейной траектории можно представить как сумму двух движений, протекающих независимо друг от друга – движения с ускорением свободного падения вдоль оси OY и равномерного прямолинейного движения вдоль оси OX. На рис. 2 изображен вектор начальной скорости тела и его проекции на координатные оси. 
| Рисунок 2. Движение тела, брошенного под углом к горизонту. Разложение вектора начальной скорости тела по координатным осям | Таким образом, для движения вдоль оси OX имеем следующие условия: | x0 = 0, υ0x = υ0 cos α, ax = 0, | а для движения вдоль оси OY | y0 = 0, υ0y = υ0 sin α, ay = –g. | Приведем здесь некоторые формулы, описывающие движение тела, брошенного под углом α к горизонту. Время полета: Дальность полета: Максимальная высота подъема:
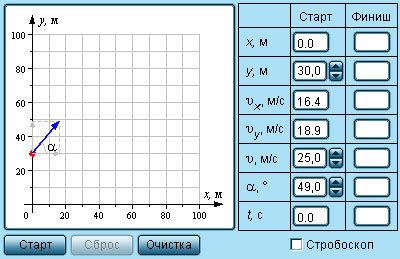
| Модель. Движение тела, брошенного под углом к горизонту | Движение тела, брошенного под углом к горизонту, происходит по параболической траектории. В реальных условиях такое движение может быть в значительной степени искажено из-за сопротивления воздуха, которое может во много раз уменьшить дальность полета тела. |
 Скачать 5.42 Mb.
Скачать 5.42 Mb.